?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In this paper, based on the bilinear form and two new test functions, for the (2 + 1)-dimensional Ito equation, we obtain non-elastic interactional solutions composed of three different types of waves including the solitary wave, the periodic wave and the lump wave, and elastic interactional solutions with the solitary wave and the lump wave. We also obtain the periodic wave solutions and two-lump wave solutions.
1. Introduction
The exact solutions of non-linear evolution equations have attracted much attention due to their wide applications in fluid mechanics, optics and plasma. There are many methods to obtain exact solutions, such as the inverse scattering method (Ablowitz & Segur, Citation1981), the Bäklund transformation method (Rogers & Schief, Citation2002), the Darboux transformation method (Gu et al., Citation2005) and the Hirota bilinear method (Hirota, Citation2004), etc. The Hirota bilinear method is a practical method in finding multiple soliton solutions, rational solutions and periodic solutions. In this paper, we will study the exact solutions of the (2 + 1)-dimensional Ito equation by using of the Hirota bilinear method with two new test functions.
In Ito (Citation1980), with the transformation , from the bilinear form
(1)
(1)
where
Ito obtained the (1 + 1)-dimensional Ito equation
(2)
(2)
which has the same 1-soliton solution as that of the KdV equation. However, the multi-soliton solutions differ in the phase shift. Some explicit solutions of the (1 + 1)-dimensional Ito EquationEquation (2)
(2)
(2) have been obtained in Hu and Li (Citation1991); Zhang and Chen (Citation1991); Li and Zeng (Citation2007). In WazWaz (Citation2008), with the generalized bilinear form of (1)
(3)
(3)
and through the transformation
(4)
(4)
Wazwaz presented the (2 + 1)-dimensional Ito equation
(5)
(5)
where α and β are constants.
For the (2 + 1)-dimensional Ito EquationEquation (5)(5)
(5) , based on the bilinear form and different test functions, different types of solutions have been obtained. In WazWaz (Citation2008), Wazwaz obtained multiple-soliton solutions by using exp-type test function. In Li and Zhao (Citation2009), Li and Zhao obtained periodic solutions and soliton solutions with exp + cos + exp-type test function. The three-wave solutions were obtained in Zhao, Dai, and Wang (Citation2010) with exp + cos + sinh-type test function. The breather-wave and the rational rogue wave solutions were provided in Wang, Tian, Qin, and Zhang (Citation2017) with exp + cos-type and exp-type test function. In Tang, Tao, and Guan (Citation2016); Yang, Ma, and Qin (Citation2017); Ma, Yong, and Zhang (Citation2017); Zou, Yu, Tian, Feng, and Li (Citation2018), the lump and the lump-soliton solutions were obtained with rational-type, rational + exp-type and rational + cosh-type test functions.
Solitary wave solutions, periodic wave solutions and lump wave solutions of non-linear evolution equations are of great significance in theory and practice (see Chen, Yan, & Zhang, Citation2003; Wazwaz, Citation2016; Zhang & Chen, Citation2016; Zhang, Liu, & Ren, Citation2008; Luo, Duan, Liu, & Liu, Citation2010; Ma, Citation2015; Zhang, Dong, Zhang, & Yang, Citation2017). The interactions of solitary waves, periodic waves and lump waves for non-linear evolution equations have attracted much attention in Kaup (Citation1981); Fokas, Pelinovsky, and Sulem (Citation2001); Lu, Tian, and Grimshaw (Citation2004); Baronio, Degasperis, Conforti, and Wabnitz (Citation2012); Rao, Cheng, and He (Citation2017); Huang and Chen (Citation2017); Wang, Wang, Zhang, and Temuer (Citation2017). For the above mentioned exact solutions of the (2 + 1)-dimensional Ito EquationEquation (5)(5)
(5) , the interactions of solitary waves are elastic and the interactions of different types of waves are inelastic. The interactions consist of only two types of waves in solitary wave, periodic wave and lump wave.
There are two aims in our work. One aim is to obtain periodic solutions and non-elastic interactional solutions composed of three different types of waves including the solitary wave, the periodic wave and the lump wave by constructing the rational + cosh + cos-type test function. This is described in Section 2. The other aim is to obtain an elastic interactional solution with the solitary wave and the lump wave by constructing the rational + rational*exp type test function and this is studied in detail in Section 3. Finally, we give our conclusions in Section 4.
2. Periodic wave solutions and nonelastic interactional solutions
In this section, based on the bilinear form Equation(3)(3)
(3) , we construct rational + cosh + cos-type test function and discuss periodic wave solutions and interactional solutions with the solitary wave, the periodic wave and the lump wave for the (2 + 1)-dimensional Ito EquationEquation (5)
(5)
(5) .
We assume the test function has the following form
(6)
(6)
where ai
, kj (j = 1, 2, 3), p and q are real constants, mj (j = 1, 2, 3) are real or pure imaginary constants and are real without specification. If ai = 0
, the test function f is similar to that in Li (Citation2009), Zhao (Citation2010), Wang (Citation2017), and Zou et al. (Citation2018). If p = 0 or q = 0, the test function f is similar to that in Tang et al. (Citation2016), Yang et al. (Citation2017), and Ma et al. (Citation2017).
Substituting Equation(6)(6)
(6) into the bilinear form Equation(3)
(3)
(3) and equating all the coefficients of independent variables to zeros, we get a set of algebraic equations:
(7)
(7)
(8)
(8)
We note that the relations in EquationEquation (7)(7)
(7) are the same as those in Yang et al. (Citation2017), Ma et al. (Citation2017), and Zou et al. (Citation2018). The EquationEquation (8)
(8)
(8) indicates four cases
(9)
(9)
The case of p = 0 or q = 0 corresponds to that in Yang et al. (Citation2017) and Ma et al. (Citation2017). If ,
and
satisfy the principle of superposition of f.
FromEquation Equations (7)(7)
(7) and Equation(8)
(8)
(8) , we can obtain many different types of exact solutions of the Ito EquationEquation (5)
(5)
(5) . In the following, we analyse two cases in detail.
Case 1. Periodic wave solutions
In this case, we take
(10)
(10)
If m1 is a real constant, we get a new t-periodic wave solution of the Ito EquationEquation (5)(5)
(5)
(11)
(11)
when , p > 0,
, this solution is non-singular. For given y = 0, taking α = 2, β = 5,
, p = 1, q = 5, the period of the t-periodic wave solution Equation(11)
(11)
(11) is
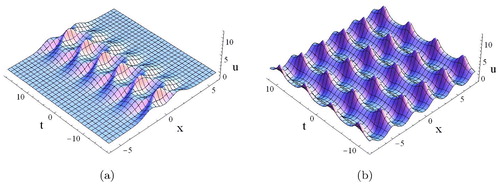
(see ).
Figure 1. Plots of the t-periodic solution (11) and the double periodic solution (12) for the Ito equation with α = 2, β = 5, , p = 1, y = 0: (a) t-periodic solution; (b) x − t double periodic solution. (a) m1 = 2, q = 5. (b)
, q = 3.
If and
is a real constant, we find a double periodic wave solution of the Ito EquationEquation (5)
(5)
(5)
(12)
(12)
when , this solution is non-singular. Taking α = 2, β = 5,
, p = 1, q = 3, the periods of the x-t double periodic wave solution Equation(12)
(12)
(12) of the Ito EquationEquation (5)
(5)
(5) are
and
(see ).
Case 2. Non-elastic interactional solutions
In this case, we take
(13)
(13)
where ai
are defined by Equation(7)
(7)
(7) .
Through the transformation Equation(4)(4)
(4) , we get a new solution of the Ito EquationEquation (5)
(5)
(5)
(14)
(14)
For the polynomial function with , as
and
, we find a lump solution and one can refer to Yang et al. (Citation2017); Ma et al. (Citation2017); Zou et al. (Citation2018) for its properties.
If we take
(15)
(15)
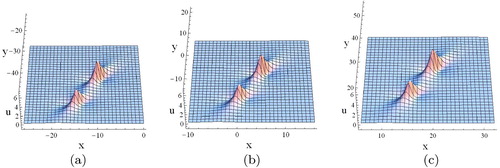
for given t = 0, this solution describes the non-elastic interactions of three different types of waves including a lump wave, a periodic wave and a solitary wave (see ). When
increases, the semi-lump wave (see ) which describes non-elastic interactions of a lump wave and a periodic wave tends to be swallowed by a solitary wave (see ).
Figure 2. Plots of the non-elastic interactional solution (14) with (13) and (15) for the Ito equation. (a) p = 0, q = 0, t = 0. (b) p = 0, q = 5, t = 0. (c) p = 4, q = 5, t = 0.
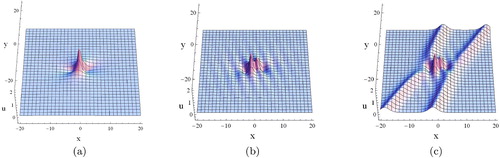
Figure 3. Plots of the non-elastic interactional solution (14) with (13) and (15) for the Ito equation. (a) p = 4, q = 5, t = −4. (b) p = 4, q = 5, t = −2. (c) p = 4, q = 5, t = 2. (d) p = 4, q = 5, t = 4.
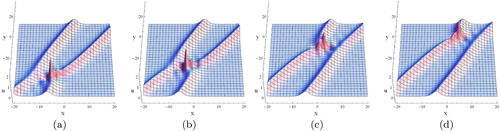
If we take
(16)
(16)
for
, this solution describes the non-elastic interactions of a solitary wave and a periodic wave (see ).
3. Elastic interactional solutions and two-lump wave solution
In this section, we propose the following novel test function
(17)
(17)
with
(18)
(18)
where ai, bi
and cj (j = 1, 2, 3) are real constants. Substituting Equation(17)
(17)
(17) into the bilinear form Equation(3)
(3)
(3) and equating all the coefficients of independent variables to zeros, we obtain a set of parameters:
(19)
(19)
(20)
(20)
In order to get non-singular solution of the Ito EquationEquation (5)(5)
(5) , we suppose
and
.
Note that g, h, satisfy the bilinear formEquation Equation (3)
(3)
(3) . Then we obtain three solutions of the Ito EquationEquation (5)
(5)
(5)
(21)
(21)
(22)
(22)
(23)
(23)
where g, h and ξ are defined by Equation(19)
(19)
(19) and Equation(20)
(20)
(20) . For given t, the stagnation points of u1 and u2 are
(24)
(24)
and
(25)
(25)
From EquationEquations (24)(24)
(24) and Equation(25)
(25)
(25) , we find that the velocities in x direction and y direction for u1 and u2 are
, respectively. Obviously, the solutions u1 and u2 are almost the same lump waves except for the difference of stagnations, and both of them move along the straight line
. Furthermore, u3 is a solitary wave, the velocities along the x-axis and the y-axis are
and
, respectively. The wave is parallel with the straight line
.
In the following, we present asymptotic analysis of the solution Equation(4)(4)
(4) with Equation(17)
(17)
(17) and we let
(26)
(26)
Taking and
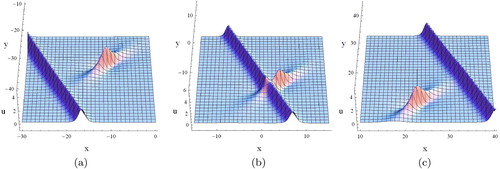
, we find an interactive phenomenon that the solitary wave catches up with the lump wave. In , the solitary wave u3 is behind the lump wave u2. Then the solitary wave u3 catches up with the lump wave u2 as shown in . Finally, the solitary wave surpasses the lump wave in . Due to the interaction with the solitary wave, the lump wave u2 is transformed into u1. The shapes, the amplitudes and the velocities of the two lump waves u1 and u2 are the same except for the phase shift. This phenomenon shows the elastic collision. The asymptotic behaviour is given by
where u1, u2 and u3 are defined byEquation Equations (21)–(23).
Figure 5. Plots of the elastic interactional solution (4) with (17), (19), (20) and (26) for the Ito equation. (a) t = −3. (b) t = 0. (c) t = 4.
When the exponential part of the test function EquationEquation (17)(17)
(17) is a function of x, y and t, the solution is an interactional solution with a solitary wave and a lump wave. In the following, we assume that the exponential part is a function of y and t only, that is
(27)
(27)
If we take
(28)
(28)
from , we find that the solution is a two-lump solution and the two-lump wave is located in a line which is parallel with
.
4. Conclusion
In this paper, by using Hirota’s bilinear method and by constructing new test functions, we obtained both non-elastic and elastic interactional solutions for the (2 + 1)-dimensional Ito equation. The non-elastic interactional solution showed the interactions among a lump wave, a periodic wave and a solitary wave. The elastic interactional solution showed the interactions between a lump wave and a solitary wave. The asymptotic behaviour of the elastic interaction was analysed. We also obtained periodic solution and two-lump solution of the (2 + 1)-dimensional Ito equation.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- Ablowitz, M. J., & Segur, H. (1981). Solitons and the inverse scattering transform. Philadelphia, PA: SIAM.
- Baronio, F., Degasperis, A., Conforti, M., & Wabnitz, S. (2012). Solutions of the vector nonlinear Schrödinger equations: Evidence for deterministic rogue waves. Physical Review Letters, 109, 044102(1)–044102(4).
- Chen, Y., Yan, Z. Y., & Zhang, H. Q. (2003). New explicit solitary wave solutions for (2 + 1)-dimensional Boussinesq equation and (3 + 1)-dimensional KP equation. Physics Letters A, 307(2–3), 107–113. doi: 10.1016/S0375-9601(02)01668-7
- Fokas, A. S., Pelinovsky, D. E., & Sulem, C. (2001). Interaction of lumps with a line soliton for the DSII equation. Physica D, 152–153, 189–198. doi: 10.1016/S0167-2789(01)00170-1
- Gu, C. H., Hu, H. S., & Zhou, Z. X. (2005). Darboux transformation in integral system: Theory and their applications to geometry. Mathematics Physics Studies (Vol. 26). New York, NY: Springer-Verlag.
- Hirota, R. (2004). The direct method in soliton theory. Cambridge: Cambridge University Press.
- Hu, X. B., & Li, Y. (1991). Nonlinear superposition formulae of the Ito equation and a model equation for shallow water waves. Journal of Physics A: Mathematical and General, 24(9), 1979–1986. doi: 10.1088/0305-4470/24/9/010
- Huang, L. L., & Chen, Y. (2017). Lump solutions and interaction phenomenon for (2 + 1)-dimensional Sawada-Kotera equation. Communications in Theoretical Physics, 67(5), 473–478. doi: 10.1088/0253-6102/67/5/473
- Ito, M. (1980). An extension of nonlinear evolution equations of the K-dV (mK-dV) type to higher orders. Journal of the Physical Society of Japan, 49(2), 771–778. doi: 10.1143/JPSJ.49.771
- Kaup, D. J. (1981). The lump solutions and the Bäcklund transformation for the three-dimensional three-wave resonant interaction. Journal of Mathematical Physics, 22(6), 1176–1181. doi: 10.1063/1.525042
- Li, C. X., & Zeng, Y. B. (2007). Soliton solutions to a higher order Ito equation: Pfaffian technique. Physics Letters A, 363(1–2), 1–4. doi: 10.1016/j.physleta.2006.10.080
- Li, D. L., & Zhao, J. X. (2009). Multiple-soliton solutions for the generalized (1 + 1)-dimensional and the generalized (2 + 1)-dimensional Ito equations. Applied Mathematics and Computation, 215(5), 1968–1974. doi: 10.1016/j.amc.2009.07.058
- Lu, Z. M., Tian, E. M., & Grimshaw, R. (2004). Interaction of two lump solitons described by the Kadomtsev-Petviashvili I equation. Wave Motion, 40(2), 123–135. doi: 10.1016/j.wavemoti.2003.12.017
- Luo, H. Y., Duan, M. Y., Liu, X., & Liu, J. (2010). Explicit periodic solitary wave solutions for the (2 + 1)-dimensional Boussinesq equation. Applied Mathematics and Computation, 217(2), 826–829. doi: 10.1016/j.amc.2010.06.023
- Ma, W. X. (2015). Lump solutions to the Kadomtsev-Petviashvili equation. Physics Letters A, 379(36), 1975–1978. doi: 10.1016/j.physleta.2015.06.061
- Ma, W. X., Yong, X. L., & Zhang, H. Q. (2017). Diversity of interaction solutions to the (2 + 1)-dimensional Ito equation. Computers and Mathematics with Applications. Advance Online Publication, 75, 289–295. doi: 10.1016/j.camwa.2017.09.013
- Rao, J. G., Cheng, Y., & He, J. S. (2017). Rational and semi-rational solutions of the nonlocal Davey-Stewartson equations. Studies in Applied Mathematics, 139(4), 568–598. doi: 10.1111/sapm.12178
- Rogers, C., & Schief, M. J. (2002). Bäcklund and Darboux transformations geometry and modern application in soliton theory. Cambridge: Cambridge University Press.
- Tang, Y. N., Tao, S. Q., & Guan, Q. (2016). Lump solitons and the interaction phenomena of them for two classes of Nonlinear Evolution equations. Computers and Mathematics with Applications, 72(9), 2334–2342. doi: 10.1016/j.camwa.2016.08.027
- Wang, X. B., Tian, S. F., Qin, C. Y., & Zhang, T. T. (2017). Dynamics of the breathers, rogue waves and solitary waves in the (2 + 1)-dimensional Ito equation. Applied Mathematics Letters, 68, 40–47. doi: 10.1016/j.aml.2016.12.009
- Wang, Y. H., Wang, H., Zhang, H. S., & Temuer, C. L. (2017). Exact interaction solutions of an extended (2 + 1)-dimensional Shallow Water Wave equation. Communications in Theoretical Physics, 68(2), 165–169. doi: 10.1088/0253-6102/68/2/165
- Wazwaz, A. M. (2008). Multiple-soliton solutions for the generalized (1 + 1)-dimensional and the generalized (2 + 1)-dimensional Ito equations. Applied Mathematics and Computation, 202(2), 840–849. doi: 10.1016/j.amc.2008.03.029
- Wazwaz, A. M. (2016). Kadomtsev-Petviashvili hierarchy: N-soliton solutions and distinct dispersion relations. Applied Mathematics Letters, 52, 74–79. doi: 10.1016/j.aml.2015.08.018
- Yang, J. Y., Ma, W. X., & Qin, Z. Y. (2017). Lump and lump-soliton solutions to the (2 + 1)-dimensional Ito equation. Analysis and Mathematical Physics, 1, 1–10.
- Zhang, C. C., & Chen, A. H. (2016). Bilinear form and new multi-soliton solutions of the classical Boussinesq-Burgers system. Applied Mathematics Letters, 58, 133–139. doi: 10.1016/j.aml.2016.02.015
- Zhang, Y., & Chen, D. Y. (1991). N-soliton-like solution of Ito equation. Communication in Theoretical Physics, 42, 641–644.
- Zhang, Y., Dong, H. H., Zhang, X. E., & Yang, H. W. (2017). Rational solutions and lump solutions to the generalized (3 + 1)-dimensional shallow water-like equation. Computers and Mathematics with Applications, 73(2), 246–252. doi: 10.1016/j.camwa.2016.11.009
- Zhang, W. G., Liu, G., & Ren, Y. C. (2008). Solitary wave solutions and periodic cosine wave solutions of nonlinear wave equations. Journal of University of Shanghai for Science and Technology, 30, 15–21.
- Zhao, Z. H., Dai, Z. D., & Wang, C. J. (2010). Extend three-wave method for the (1 + 2)-dimensional Ito equation. Applied Mathematics and Computation, 217(5), 2295–2300. doi: 10.1016/j.amc.2010.06.059
- Zou, L., Yu, Z. B., Tian, S. F., Feng, L. L., & Li, J. (2018). Lump solutions with interaction phenomena in the (2 + 1)-dimensional Ito equation. Modern Physics Letters B, 32(07), 1850104. doi: 10.1142/S021798491850104X