Effects of nonlocality and two temperature in a nonlocal thermoelastic solid due to ramp type heat source

Abstract

This investigation is focused on the effects of nonlocality due to 2-D deformations arising in a nonlocal homogeneous isotropic thermoelastic solid which is subjected to a ramp type heat source with two temperature. There has been the use of Laplace and Fourier transforms for solving the equations. The expressions for displacement components, stress components and conductive temperature have been computed in the transformed domain. The numerical inversion technique has been used for obtaining the results in the physical domain. The effect of nonlocal parameter on the displacement components, conductive temperature and stress components have been represented graphically.

Keywords:

• Eringen model of nonlocal theories
• Laplace and Fourier transforms
• nonlocal theory of thermoelasticity
• ramp type heat
• thermoelasticity

1. Introduction

The nonlocal theory of thermoelasticity considers that the various physical quantities are not just dependent upon the values of independent constitutive variables at that point only but upon those values for the whole system. Nonlocal effects are of dominant nature. Also, if the effects of strains at points other than the reference point are not considered then the results obtained are similar to the results of the classical theory. In the theory of thermoelasticity with two temperatures, the heat conduction is dependent upon the variations on two distinct temperatures; one of these is the conductive temperature while the other is thermodynamic temperature.

A Continuum theory for elastic materials was developed by Kroner (1967) for long range cohesive forces and proved the importance of range effects. A theory of nonlocal interactions was derived by Edelen and Laws (1971) agreeing to the concept of nonlocality as suggested by Kroner. Edelen, Green, and Laws (1971) obtained the constitutive equations for the theory of nonlocal elasticity termed as protoelasticity. Eringen and Edelen (1972) developed the nonlocal elasticity theory by making use of the global balance laws and the second law of thermodynamics. Wang and Dhaliwal (1993) established a reciprocity relation and addressed certain issues addressing nonlocal thermoelasticity and extended the concept of nonlocality further. Artan (1996) proved the superiority of nonlocal theory by comparing various results of both theories. The uniqueness results were derived by Marin (1997) for thermoelastic bodies with voids.

Polizzotto (2001) further refined the Eringen model of nonlocal elasticity theory. Eringen (2002) developed nonlocal continuum field theories. Paola, Failla, and Zingales (2010) presented a mechanical based approach to three-dimensional nonlocal elasticity theory and proved the high dependence of the results on the size. Simsek (2011) conducted a study for studying the influences of the nonlocal parameter. The problem of generalized thermoelasticity was discussed by Zenkour and Abbas (2014). Marin and Nicaise (2016) studied the thermoelastic behavior of dipolar bodies. Vasiliev and Lurie (2016) discussed different nonlocal elasticity theories. Marin and Craciun (2017) described that the nonlocal effects are shown by the micro-structured composites.

Khetir, Bouiadjra, Houari, Tounsi, and Mahmoud (2017) worked on the nanosized FG plates and proposed a new nonlocal deformation theory. Marin, Baleanu, and Vlase (2017) investigated the theory of micropolar thermoelastic bodies. Hassan, Marin, Ellahi, and Alamri (2018) studied the convective heat transfer. Bachher and Sarkar (2018) studied the theory of non-locality for thermoelastic materials having voids. Lata (2018a) discussed nonlocality effects for plane waves and Lata (2018b) continued the study in thermoelastic medium having sandwich layer. Lata and Singh (2019) studied the nonlocality effects for inclined load.

Chen and Gurtin (1968) investigated the heat conduction theory for the involvement of two temperatures. Youssef (2006) constructed a new theory in which the heat conduction theory for deformable bodies was considered. He gave the concept of dependence on two distinct temperatures. Abbas and Youssef (2009) analyzed the transient phenomena and proposed a new model for thermoelastic solids. Youssef and Al-Lehaibi (2010) further constructed a new model for elastic materials. Abbas and Youssef (2013) took this analysis further. Abbas (2014) extended this study to a spherical cavity. Carrera, Abouelregal, Abbas, and Zenkour (2015) studied the effect of two temperatures for a beam under the effects of a ramp type heat source. Kumar, Sharma, and Lata (2016a) investigated the disturbances under the combined effects of rotation, two temperature, Hall currents and magnetic field. Kumar, Sharma, and Lata (2016b) studied thermomechanical interactions under the effects of a rotating medium with magnetic effect and two temperature.

Ezzat, El-Karamany, and El-Bary (2016a) used a Kernel function for constructing a new model for thermoelastic materials while Ezzat and El-Bary (2016) did it for thermo viscoelastic materials. Ezzat and Ai-Bary (2017) gave a mathematical model which was based on fractional derivative heat transfer. Ezzat, El-Karamany, and El-Bary (2018) applied the memory-dependent derivatives to derive a model of magneto-thermoelasticity. Ezzat and El-Bary (2017) derived a new mathematical model based on two temperature theory along with fractional heat transfer. Lata and Singh (2020a) investigated the nonlocal parameter effects with hall current for a magneto-thermoelastic solid due to normal force and studied the effects of nonlocality on various components graphically.

Lata and Singh (2020b) studied the two temperature and nonlocal parameter effects on a homogeneous isotropic thermoelastic material in a frequency domain. Chen, Lin, and Wang (2019), Fang and Dai (2020), Wu and Dai (2020) and Wang, Lu, Dai, and Chen (2020) studied and investigated the Soliton solutions for nonlinear Schrodinger equations and discussed the diffraction effects, different nonlinear effects, evolution of optical wave etc. Abbas (2016) studied a thermoelastic body with a spherical cavity subjected to a thermal shock in the context of the theory of fractional order thermoelasticity and proved that the fractional parameter effect plays a significant role on all the physical quantities. Ezzat, El-Karamany, and El-Bary (2016b) developed a new mathematical model for magneto-thermoelastic materials with two temperature and showed the effects on various physical quantities. Abouelregal and Ahmad (2020) constructed a fractional thermoelastic modified Fourier’s law. Abo‐Dahab, Abouelregal, and Ahmad (2020) gave a thermoelastic model of fractional order and used it to discuss a problem of thermoelastic half‐space. Abdel-Khalek, Abo-Dahab, Ragab, Ahmad, and Rawa (2020) studied the dynamical behavior of the geometric phase based on the engineering of a three-level atomic configuration and the effect of energy dissipation of the dynamical properties of the geometric phase.

Here, in this paper the effects of nonlocality and two temperature in a homogeneous isotropic nonlocal homogeneous thermoelastic solid under ramp type heat source have been discussed and the effects on the displacement components, stress components and conductive temperature have been computed numerically and depicted graphically.

2. Basic equations

Following Youssef (2006) and Eringen (2002), the equations of motion and the constitutive relations for a homogeneous isotropic nonlocal thermoelastic solid with two temperature are given by (1) $$(\mathrm{\lambda }+2\mu )\nabla (\nabla .\mathit{u}\mathbf{)}-\mu (\nabla \times \nabla \times \mathit{u}\mathbf{)}-\beta \nabla \theta =(1-{ϵ}^2{\nabla }^2)\rho \frac{{\partial }^2\mathit{u}}{\partial t^2},$$(1) (2) $$K^{\mathrm{*}}{\nabla }^2\phi = \rho C^{\mathrm{*}}\frac{\partial \theta }{\partial t}+ \beta {\theta }_0\frac{\partial }{\partial t} (\nabla .u),$$(2)

where (3) $$\theta =\left(1-a{\nabla }^2\right) \phi ,$$(3) (4) $$t_{ij}=\lambda u_{k,k}{\delta }_{ij}+\mu \left(u_{i,j}+u_{j,i}\right)- \beta \theta {\delta }_{ij}.$$(4) where$ϵ$ is the nonlocal parameter, $\phi$ is the conductive temperature, $\rho$ corresponds to the mass density, the displacement vector corresponds to $\mathit{u}$=($u_1,0,u_3),$$a$ is two temperature parameter, ${\theta }_0$ is reference temperature while $\theta$ is thermodynamic temperature, $C^{*}$ is the specific heat, $K^{*}$ is the thermal conductivity coefficient, $\beta =(3+2\mathrm{\mu })\mathrm{\alpha }$ where $\lambda , \mu$ are material constants and$\mathrm{\alpha }$ is thermal expansion coefficient, $e_{ij}$ corresponds to strain tensor components, $e_{kk}$ is dilatation, ${\delta }_{ij}$ is the Kronecker delta and $t_{ij}$ are the stress tensor components.

3. Formulation of the problem

A nonlocal homogeneous isotropic thermoelastic solid is considered in an initially undeformed state at temperature${ \theta }_0.$ We take a rectangular Cartesian co-ordinate system $(x_1, x_2, x_3)$ with $x_3$-axis pointing normally into the half-space, which is thus represented by $x_3\ge 0.$ We consider the plane such that all particles on a line parallel to $x_2$-axis are equally displaced, so that the field components $u_2=0$ and $u_1,u_3$ and $\phi$ are independent of $x_2.$ We restrict our analysis to two-dimensional problem i.e., (5) $$\mathit{u} =(u_1,0,u_3).$$(5)

Using Equation (5)(5) $$\mathit{u} =(u_1,0,u_3).$$(5) in Equations (1)(1) $$(\mathrm{\lambda }+2\mu )\nabla (\nabla .\mathit{u}\mathbf{)}-\mu (\nabla \times \nabla \times \mathit{u}\mathbf{)}-\beta \nabla \theta =(1-{ϵ}^2{\nabla }^2)\rho \frac{{\partial }^2\mathit{u}}{\partial t^2},$$(1) and (2)(2) $$K^{\mathrm{*}}{\nabla }^2\phi = \rho C^{\mathrm{*}}\frac{\partial \theta }{\partial t}+ \beta {\theta }_0\frac{\partial }{\partial t} (\nabla .u),$$(2) , yields (6) $$\left(\lambda +\mu \right)\frac{\partial e}{\partial x_1}+\mu {\nabla }^2{u}_1-\beta \frac{\partial \theta }{\partial x_1}=\left(1-{ϵ}^2{\nabla }^2\right) \rho \frac{{\partial }^2{u}_1}{\partial t^2},$$(6) (7) $$\left(\lambda +\mu \right)\frac{\partial e}{\partial x_3}+\mu {\nabla }^2{u}_3-\beta \frac{\partial \theta }{\partial x_3}=\left(1-{ϵ}^2{\nabla }^2\right) \rho \frac{{\partial }^2{u}_3}{\partial t^2},$$(7) (8) $$K^{\mathrm{*}}{\nabla }^2\phi = \rho C^{\mathrm{*}}\frac{\partial \theta }{\partial t}+ \beta {\theta }_0\frac{\partial e}{\partial t},$$(8) where,$e=\frac{\partial u_1}{\partial x_1}+\frac{\partial u_3}{\partial x_3},$${ \nabla }^2=\frac{{\partial }^2}{\partial x_1^2}+\frac{{\partial }^2}{\partial x_3^2}.$

We define the following dimensionless quantities (9) $$\left(x_1^{\mathrm{\prime }}, x_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(x_{1,}{x}_3\right), \left(u_1^{\mathrm{\prime }}, u_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(u_{1,}{u}_3\right),t_{ij}^{\mathrm{\prime }}=\frac{t_{ij}}{\beta T_0}, t^{\mathrm{\prime }}={\omega }_{1}t, a^{\mathrm{\prime }}=\frac{{\omega }_1^2}{c_1^2}a \mathit{and} {\mathrm{K}}_n^{\mathrm{\prime }}=\frac{c_1}{\lambda {\omega }_1}{K}_n$$(9) where, $c_1^2=\frac{\mu }{\rho }$ and ${\omega }_1= \frac{\rho C^{\mathrm{*}}{c}_1^2}{K^{\mathrm{*}}}.$

Upon introducing the quantities defined by Equation (9)(9) $$\left(x_1^{\mathrm{\prime }}, x_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(x_{1,}{x}_3\right), \left(u_1^{\mathrm{\prime }}, u_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(u_{1,}{u}_3\right),t_{ij}^{\mathrm{\prime }}=\frac{t_{ij}}{\beta T_0}, t^{\mathrm{\prime }}={\omega }_{1}t, a^{\mathrm{\prime }}=\frac{{\omega }_1^2}{c_1^2}a \mathit{and} {\mathrm{K}}_n^{\mathrm{\prime }}=\frac{c_1}{\lambda {\omega }_1}{K}_n$$(9) in Equations (6)–(8)(6) $$\left(\lambda +\mu \right)\frac{\partial e}{\partial x_1}+\mu {\nabla }^2{u}_1-\beta \frac{\partial \theta }{\partial x_1}=\left(1-{ϵ}^2{\nabla }^2\right) \rho \frac{{\partial }^2{u}_1}{\partial t^2},$$(6) , and suppressing the primes, yields (10) $$\left(\frac{\lambda +2\mu }{\mu }\right)\frac{{\partial }^2{u}_1}{\partial {x_1}^2}+\left(\frac{\lambda +\mu }{\mu }\right)\frac{{\partial }^2{u}_3}{\partial x_1\partial x_3}+\frac{{\partial }^2{u}_1}{\partial {x_3}^2}-\beta \frac{{\theta }_0}{\mu }\frac{\partial \theta }{\partial x_1}=\left(1-{ϵ}^2{\nabla }^2\right)\frac{{\partial }^2{u}_1}{\partial t^2},$$(10) (11) $$\left(\frac{\lambda +2\mu }{\mu }\right)\frac{{\partial }^2{u}_3}{\partial {x_3}^2}+\left(\frac{\lambda +\mu }{\mu }\right)\frac{{\partial }^2{u}_1}{\partial x_1\partial x_3}+\frac{{\partial }^2{u}_3}{\partial {x_1}^2}-\beta \frac{{\theta }_0}{\mu }\frac{\partial \theta }{\partial x_3}=\left(1-{ϵ}^2{\nabla }^2\right)\frac{{\partial }^2{u}_3}{\partial t^2},$$(11) (12) $${\nabla }^2\phi -\frac{\rho C^{\mathrm{*}}{c_1}^2}{K^{\mathrm{*}}{\omega }_1}\frac{\partial }{\partial t}\left(1-a{\nabla }^2\right) \phi = \frac{\beta {c_1}^2}{K^{\mathrm{*}}{{\omega }_1}^2}\frac{\partial }{\partial t}\left(\frac{\partial {\mathrm{u}}_1}{\partial x_1}+\frac{\partial u_3}{\partial x_3}\right).$$(12)

Introducing potential functions defined by (13) $$u_1=\frac{\partial \mathrm{q}}{\partial x_1}-\frac{\partial \mathrm{\psi }}{\partial x_3}, u_3=\frac{\partial \mathrm{q}}{\partial x_3}+\frac{\partial \mathrm{\psi }}{\partial x_1}$$(13) where, $\mathrm{q}\left(x_1,x_3,t\right)$ and $\mathrm{\psi }\left(x_1,x_3,t\right)$ are scalar potential functions.

Using Equation (13)(13) $$u_1=\frac{\partial \mathrm{q}}{\partial x_1}-\frac{\partial \mathrm{\psi }}{\partial x_3}, u_3=\frac{\partial \mathrm{q}}{\partial x_3}+\frac{\partial \mathrm{\psi }}{\partial x_1}$$(13) in Equations (10)–(12)(10) $$\left(\frac{\lambda +2\mu }{\mu }\right)\frac{{\partial }^2{u}_1}{\partial {x_1}^2}+\left(\frac{\lambda +\mu }{\mu }\right)\frac{{\partial }^2{u}_3}{\partial x_1\partial x_3}+\frac{{\partial }^2{u}_1}{\partial {x_3}^2}-\beta \frac{{\theta }_0}{\mu }\frac{\partial \theta }{\partial x_1}=\left(1-{ϵ}^2{\nabla }^2\right)\frac{{\partial }^2{u}_1}{\partial t^2},$$(10) , and applying Laplace and Fourier transforms defined by (14) $$\overline{f}\left(x_1,x_3,s\right)={\int }_0^{\mathrm{\infty }}f\left(x_1,x_3,t\right)e^{-st}dt,$$(14) (15) $$\widehat{f}\left(\mathrm{\xi },x_3,s\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\overline{f}\left(x_1,x_3,s\right)e^{i\mathrm{\xi }{x}_1}d{x}_1.$$(15)

On the resulting equations, a system of homogeneous equations is obtained as follows, (16) $$\left[\left(a_1+{ϵ}^2{s}^2\right)\frac{d^2}{d{x}_3^2}-\left({a_1\xi }^2+s^2+{ϵ}^2{\mathrm{\xi }}^2\right)\right]\widehat{q}-a_2\left[1+a{\xi }^2-a\frac{d^2}{d{x}_3^2}\right]\widehat{\phi }=0,$$(16) (17) $$\left[\left(1+{ϵ}^2{\mathrm{s}}^2\right)\frac{d^2}{d{x}_3^2}-\left({\mathrm{s}}^2{+\xi }^2{+{ϵ}^2{\mathrm{s}}^2\xi }^2\right)\right]\widehat{\mathrm{\psi }}=0,$$(17) (18) $$\left\{a_{4}s\left({-\xi }^2+\frac{d^2}{d{x}_3^2}\right)\right\}\widehat{q}-\left\{(1+a{a}_{3}s)\frac{d^2}{d{x}_3^2}-({\xi }^2+a_{3}s+{aa}_{3}s{\xi }^2)\right\}\widehat{\phi }= 0.$$(18) where, $a_1=\frac{\lambda +2\mu }{\mu },$ $a_2=\beta \frac{{\theta }_0}{\mu },$ $a_3=\frac{\rho C^{\mathrm{*}}{c_1}^2}{K^{\mathrm{*}}{\omega }_1}$ and $a_4=\frac{\beta {c_1}^2}{K^{\mathrm{*}}{{\omega }_1}^2}.$

The system of Equations (16)–(18)(16) $$\left[\left(a_1+{ϵ}^2{s}^2\right)\frac{d^2}{d{x}_3^2}-\left({a_1\xi }^2+s^2+{ϵ}^2{\mathrm{\xi }}^2\right)\right]\widehat{q}-a_2\left[1+a{\xi }^2-a\frac{d^2}{d{x}_3^2}\right]\widehat{\phi }=0,$$(16) , will have a nontrivial solution if the determinant of coefficient $\widehat{q} \mathit{and} \widehat{\phi }$ is vanished to give characteristic equations as (19) $$\left[\mathrm{P}\frac{d^4}{d{x}_3^4}+Q\frac{d^2}{d{x}_3^2}+R\right](\widehat{q},\widehat{\phi })=0,$$(19) (20) $$\left[P\mathrm{\prime }\frac{d^2}{d{x}_3^2}-Q\mathrm{\prime } \right]\widehat{\mathrm{\psi }}=0.$$(20) where, $\mathrm{P}={-[a}_1+a{a}_1{a}_{3}s+{ϵ}^2{s}^2+a{a}_3{ϵ}^2{s}^3+a{a}_2{a}_{4}s],$ $$Q=2a_1{\xi }^2+{a_{2}a}_{4}s+2{a{a}_{2}a}_{4}s{\xi }^2+a{a}_{3}s{ϵ}^2{\mathrm{\xi }}^2\left(1+s^2\right)+{2aa}_1{a}_{3}s{\xi }^2+{a_{1}a}_{3}s+s^2+a{a}_3{s}^3+{ϵ}^2{\mathrm{\xi }}^2\left(1+s^2\right),$$ $$R=-\left[\right(a_1+a{a}_{3}s{ϵ}^2+{ϵ}^2+a{a}_1{a}_{3}s+{aa}_2{a}_{4}s){\xi }^4+(a_1{a}_{3}s+s^2+a{a}_3{s}^3+a_{3}s{ϵ}^2+a_2{a}_{4}s){\xi }^2+a_3{s}^3,$$

$P^{\mathrm{\prime }}=\left(1+{ϵ}^2{\mathrm{s}}^2\right)$ and $Q^{\mathrm{\prime }}=\left({\mathrm{s}}^2{+\xi }^2{+{ϵ}^2{\mathrm{s}}^2\xi }^2\right).$

The roots of Equation (19)(19) $$\left[\mathrm{P}\frac{d^4}{d{x}_3^4}+Q\frac{d^2}{d{x}_3^2}+R\right](\widehat{q},\widehat{\phi })=0,$$(19) are $\pm {\lambda }_i\left(i=1,2\right)$ and of (20(20) $$\left[P\mathrm{\prime }\frac{d^2}{d{x}_3^2}-Q\mathrm{\prime } \right]\widehat{\mathrm{\psi }}=0.$$(20) ) are $\pm {\lambda }_3$ which are obtained by using the radiation conditions that $\widehat{q},\widehat{\phi }\to 0$ as $x_3\to \infty .$ Then the solutions of these equations are written as, (21) $$\widehat{q}=A_1{e}^{-{{\lambda }_{1}x}_3}+A_2{e}^{-{{\lambda }_{2}x}_3},$$(21) (22) $$\widehat{\phi }=d_1{A}_1{e}^{-{{\lambda }_{1}x}_3}+d_2{A}_2{e}^{-{{\lambda }_{2}x}_3},$$(22) (23) $$\widehat{\mathrm{\psi }}=A_3{e}^{-{{\lambda }_{3}x}_3}.$$(23) where, $$d_i=\frac{\left(1+a{a}_{3}s\right){{\lambda }_i}^2-\left({\xi }^2+a_{3}s+{aa}_{3}s{\xi }^2\right)}{\left(a_1+{ϵ}^2{s}^2\right){{\lambda }_i}^2-\left({a_1\xi }^2+s^2+{ϵ}^2{\mathrm{\xi }}^2\right)} i=1,2.$$

3.1. Boundary conditions

The boundary conditions are given by: (24) $$\left(1\right) t_{33}\left(x_1,x_3,t\right)=0,$$(24) (25) $$\mathrm{(2)} t_{31}\left(x_1,x_3,t\right)=0.$$(25)

The boundary of the half-space is affected by ramp-type heating, which depends upon co-ordinate $x_1$ and time t of the form (26) $$(3) \phi \left(x_1,0,t\right)=G\left(t\right)\delta \left(x_1\right).$$(26) where, $\delta (x_1)$ is dirac delta function of $x_1$ while $G(t)$ is a function defined as follows: (27) $$G\left(t\right)=\{\begin{array}{l}0, t\le 0\\ T_1\frac{t}{t_0}, 0<t\le t_0\\ T_1, t>t_0\end{array},$$(27) where $t_0$ corresponds to the length of the time required to raise the heat while $T_1$ is a constant. It means that the boundary of the half space is at a fixed temperature${ t}_0$ and at rest initially. Then it is suddenly raised to a temperature which is equal to a function $G\left(t\right)\delta (x_1)$ and then is maintained at this temperature.

Laplace and Fourier transforms are applied to both sides of (26) so that we get, (28) $$\widehat{\overline{\phi }}\left(x_1,0,s\right)=\overline{G}\left(s\right),$$(28) where $\overline{G}\left(s\right)=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}.$

By making use of the dimensionless quantities defined by (9(9) $$\left(x_1^{\mathrm{\prime }}, x_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(x_{1,}{x}_3\right), \left(u_1^{\mathrm{\prime }}, u_3^{\mathrm{\prime }}\right)=\frac{{\omega }_1}{c_1}\left(u_{1,}{u}_3\right),t_{ij}^{\mathrm{\prime }}=\frac{t_{ij}}{\beta T_0}, t^{\mathrm{\prime }}={\omega }_{1}t, a^{\mathrm{\prime }}=\frac{{\omega }_1^2}{c_1^2}a \mathit{and} {\mathrm{K}}_n^{\mathrm{\prime }}=\frac{c_1}{\lambda {\omega }_1}{K}_n$$(9) ), with the aid of (4(4) $$t_{ij}=\lambda u_{k,k}{\delta }_{ij}+\mu \left(u_{i,j}+u_{j,i}\right)- \beta \theta {\delta }_{ij}.$$(4) ), (14(14) $$\overline{f}\left(x_1,x_3,s\right)={\int }_0^{\mathrm{\infty }}f\left(x_1,x_3,t\right)e^{-st}dt,$$(14) )–(15(15) $$\widehat{f}\left(\mathrm{\xi },x_3,s\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\overline{f}\left(x_1,x_3,s\right)e^{i\mathrm{\xi }{x}_1}d{x}_1.$$(15) ) and (21(21) $$\widehat{q}=A_1{e}^{-{{\lambda }_{1}x}_3}+A_2{e}^{-{{\lambda }_{2}x}_3},$$(21) )–(23(23) $$\widehat{\mathrm{\psi }}=A_3{e}^{-{{\lambda }_{3}x}_3}.$$(23) ), the displacement components, stress components and conductive temperature are obtained (29) $$\widehat{\overline{u_1}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{\mathrm{t}}_0{s}^2}\left\{\left[ \iota \xi (M_1+M_2)\right]+{\lambda }_3{M}_3\right\},$$(29) (30) $$\widehat{\overline{u_3}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}\left[{-\lambda }_1{M}_1{-\lambda }_2{M}_2+\iota \xi M_3\right],$$(30) (31) $$\widehat{\overline{t_{11}}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}\{[{\xi }^2(\lambda +2\mu )+\beta d_1(1+a{\xi }^2-a{{\lambda }_1}^2)](-M_1)+[{\xi }^2(\lambda +2\mu )+\beta d_2(1+a{\xi }^2-a{{\lambda }_2}^2)](-M_2)+\iota \xi (\lambda +2\mu ){\lambda }_3{M}_3\},$$(31) (32) $$\widehat{\overline{\theta }}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}\left\{M_1{d}_1+M_2{d}_2\right\},$$(32) (33) $$\widehat{\overline{t_{33}}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}\{[{{\lambda }_1}^2(\lambda +2\mu )-\beta d_1(1+a{\xi }^2-a{{\lambda }_1}^2)-\lambda {\xi }^2]M_1+[{{\lambda }_2}^2(\lambda +2\mu )-\beta d_2(1+a{\xi }^2-a{{\lambda }_2}^2)-\lambda {\xi }^2]M_2-\iota \xi (\lambda +2\mu ){\lambda }_3{M}_3\},$$(33) (34) $$\widehat{\overline{t_{31}}}=-\mu T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{t}_0{s}^2}\left\{2\iota \xi {(\lambda }_1{M}_1+{\lambda }_2{M}_2)+({{\lambda }_3}^2+{\mathit{\xi }}^2)M_3\right\},$$(34) $$\mathrm{where}, \Delta = \mu {{(\lambda }_3}^2+{\mathit{\xi }}^2\left){[\lambda {\mathit{\xi }}^2(d_2-d_1)+(\lambda +2\mu )({{\lambda }_2}^2{d}_1-{{\lambda }_1}^2{d}_2)]+\beta a\mu \frac{{\theta }_0{{\omega }_1}^2}{{c_1}^2}[{d_{1}d}_2({{\lambda }_2}^2-{{\lambda }_1}^2)({{\lambda }_3}^2+{\mathit{\xi }}^2)]-4{\mu }^2{\mathit{\xi }}^2\lambda }_3\right({\lambda }_2{d}_1-{\lambda }_1{d}_2).$$

4. Particular cases

1. If $\mathrm{a}=0,$ then from Equations (29)–(34)(29) $$\widehat{\overline{u_1}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{\mathrm{t}}_0{s}^2}\left\{\left[ \iota \xi (M_1+M_2)\right]+{\lambda }_3{M}_3\right\},$$(29) , the corresponding expressions for displacement components, stress components and conductive temperature for nonlocal homogeneous isotropic solid without effect of two temperature are obtained.

2. For $ϵ$ = 0, the corresponding expressions for isotropic solid without nonlocal effects and with two temperature are obtained from Equations (29)–(34)(29) $$\widehat{\overline{u_1}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{\mathrm{t}}_0{s}^2}\left\{\left[ \iota \xi (M_1+M_2)\right]+{\lambda }_3{M}_3\right\},$$(29) .

5. Inversion of the transformation

For obtaining the solution in physical domain, the transforms in Equations (29)–(34)(29) $$\widehat{\overline{u_1}}=T_1\frac{(1-e^{-s{t}_0})}{\mathrm{\Delta }{\mathrm{t}}_0{s}^2}\left\{\left[ \iota \xi (M_1+M_2)\right]+{\lambda }_3{M}_3\right\},$$(29) are to be inverted. The conductive temperature and the components for displacement and stresses are functions of $x_3,$ $s$ and $\xi$ respectively and thus of the form$f(\xi , x_3, s).$ So, for obtaining the function$f(x_1, x_3, t)$ in the physical domain, the Fourier transform will be inverted using (35) $$\overline{f}\left(x_1, x_3, s\right)=\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-i\xi x_1}\widehat{f}\left(\xi , x_3, s\right)d\xi =\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left|\text{cos}\left(\xi x_1\right)f_e-i\text{sin}\left(\xi x_1\right)f_0\right|d\xi$$(35) where $f_{0 }$ and $f_e$ are the odd and even parts of $\widehat{f}\left(\xi , x_3, s\right)$ respectively. So that Equation (35)(35) $$\overline{f}\left(x_1, x_3, s\right)=\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-i\xi x_1}\widehat{f}\left(\xi , x_3, s\right)d\xi =\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left|\text{cos}\left(\xi x_1\right)f_e-i\text{sin}\left(\xi x_1\right)f_0\right|d\xi$$(35) gives the Laplace transform $\overline{f}\left(x_1, x_3, s\right)$ of the function$f(x_1, x_3, t).$ Now, the Laplace transform function $\overline{f}\left(x_1, x_3, s\right)$ can be inverted to $f(x_1, x_3, t)$ using Honig and Hirdes (1984). Then, the integral in Equation (35)(35) $$\overline{f}\left(x_1, x_3, s\right)=\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-i\xi x_1}\widehat{f}\left(\xi , x_3, s\right)d\xi =\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left|\text{cos}\left(\xi x_1\right)f_e-i\text{sin}\left(\xi x_1\right)f_0\right|d\xi$$(35) is to be calculated. The method as prescribed in Press, Teukolshy, Vellerling, and Flannery (1986) has been applied for evaluation of this integral. Romberg’s integration with adequate step size along with the results from successive refinements of the extended trapezoidal rule have also been utilized for this purpose.

6. Numerical results

Magnesium material has been selected for numerical calculations. The physical data for which is given as below: $$\lambda =9.4\times {10}^{10}N{m}^{-2}, \mu =3.278\times {10}^{10}N{m}^{-2}, K^{\mathrm{*}}=1.7\times {10}^{2}W{m}^{-1}{K}^{-1}, \rho =1.74\times {10}^{3}K{gm}^{-3}, T_0=298 K, C^{\mathrm{*}}=10.4\times {10}^{2}JK{g}^{-1}{\mathrm{deg}}^{-1}, {\omega }_1=3.58, a=0.05.$$

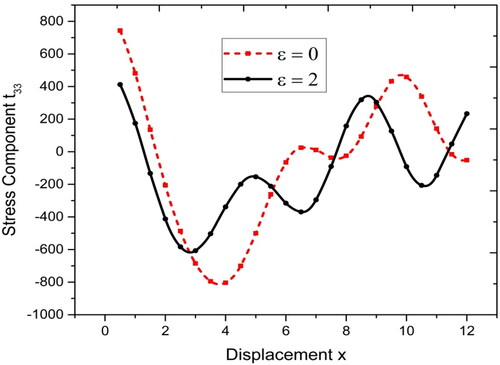
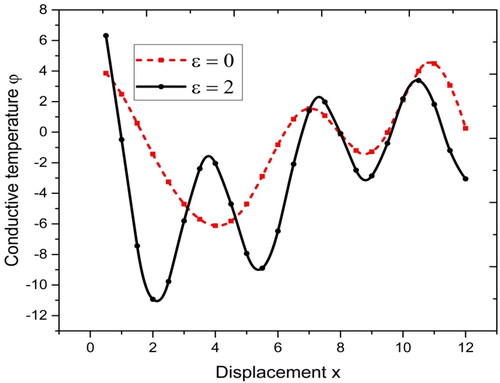
A comparison of values w.r.t. distance has been made for the components of displacements, stresses and conductive temperature for local $ϵ=0$ and nonlocal parameter $ϵ=2.0$ and is presented graphically in Figures 1–6.

Figure 1. Variation of displacement component $u_1$ with displacement.

Figure 2. Variation of displacement component$u_3$ with displacement.

Figure 3. Variation of stress component${ t}_{11}$ with displacement.

Figure 4. Variation of stress component$t_{31}$ with displacement.

Figure 5. Variation of stress component${ t}_{33}$ with displacement.

Figure 6. Variation of conductive temperature$\phi$ with displacement.

1. The solid line having black color with circles as center symbol corresponds to $ϵ=2.$

2. The dotted red colored line with squares as center symbol corresponds to $ϵ=0.$

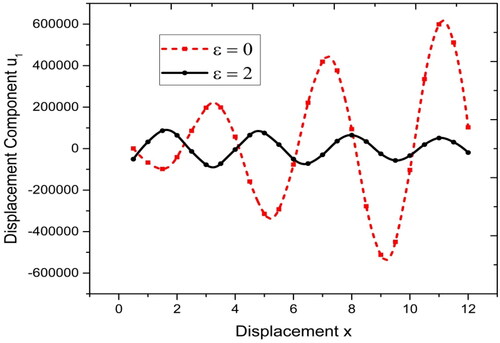
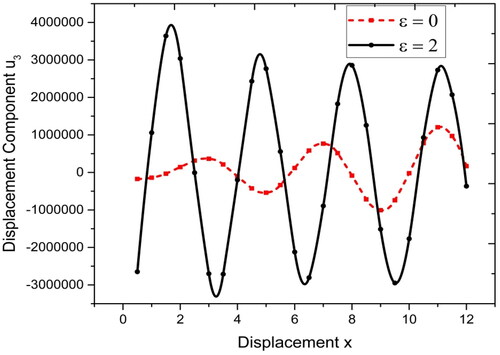
From Figure 1 it is clearly visible that the variations of normal displacement $u_1$ for local and non local parameters are different. For $\epsilon =0$ the variations are oscillatory and also there is an increase in upward and downward variations while for $\epsilon =2$ the variations are oscillatory but with constant variations. 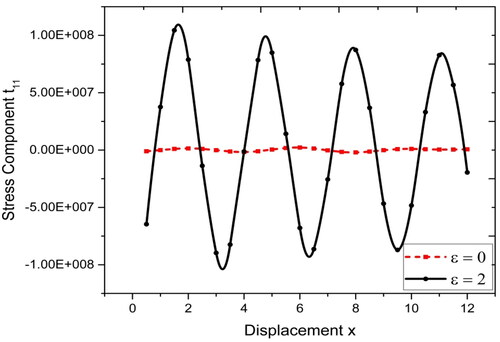From Figure 2, it has been observed that for both local and nonlocal parameters, the variations of normal displacement $u_3$ are different while for $\epsilon =0$ the variations are less oscillatory for $x<5$ and more oscillatory for $x>5$ but for $\epsilon =2$ the variations are oscillatory with more variations in the starting and with decreasing oscillations with increase in displacement. 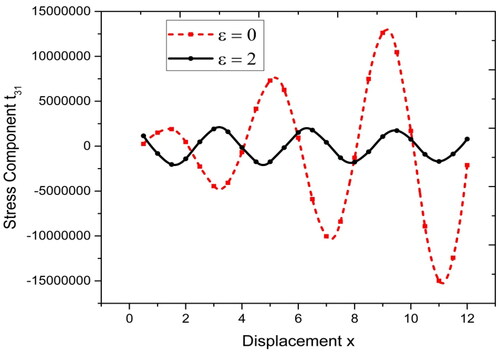As evident from Figure 3, for $\epsilon =2$ the variations for normal stress follow high variation oscillatory path with slightly decreasing variations later but with almost a constant path with slight oscillations for $\epsilon =0.$ From Figure 4, the variations of tangential stress $t_{11}$ for local and nonlocal parameters have been shown as following oscillatory path. For $\epsilon =0,$ the variations are more oscillatory and with increasing magnitude of variations while for $\epsilon =2,$ the variations are oscillatory with almost constant magnitude of variations. In Figure 5, the variations of normal stress $t_{33}$ with displacement are shown. It is clear that the variations for both local as well as nonlocal parameters decrease for starting values of x, then increasing with small oscillations. The variations for local and nonlocal parameters are clearly distinct in the figure. Form Figure 6. It is clear that the variations of conductive temperature $\phi$ for local and nonlocal parameters are distinctive and oscillatory in nature. For $\epsilon =0,$ the variations are slightly less oscillatory in terms of magnitude of oscillations as compared to $\epsilon =2.$

7. Conclusion

In the above discussion the numerical results have been computed and depicted graphically showing the effects of nonlocal parameter on conductive temperature and the components of displacements and stresses. From the graphs, it is concluded that variations for different components is following oscillatory paths for most of the values of displacement but the variations are different for nonlocal and local parameter. It is observed that there is a significant impact due to the concept of nonlocality and thus the parameter cannot be ignored. The Ramp type heat source used in this investigation has shown clear variations for the local and nonlocal parameters. These results can be of utmost importance for the researchers in the field of material sciences, mechanics, geophysics, acoustics etc.

Disclosure statement

There is no conflict of interest with anyone.