Homotopy analysis approach to study the dynamics of fractional deterministic Lotka-Volterra model

Abstract

The population dynamics of two species that is governed by the deterministic Lotka-Volterra model concerned with the interaction of predator and prey is investigated in this article as an application of homotopy analysis method. The analytical approximate solution in the form of convergent infinite series is obtained by considering the time-fractional derivatives in the Caputo sense. The simulation of obtained results exhibit the effect of variation in fractional parameters, auxiliary parameters and auxiliary linear operators on the mass concentration of both the biological species which in turn affects the structure of the system.

Keywords:

• Homotopy analysis method
• Lotka-Volterra model
• Caputo fractional derivative

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 92D25
• 65L03

1. Introduction and preliminaries

The ecological mathematics has emerged as a subject which has recently attracted the attention of mathematicians and biologists as it helps in understanding the evolution of the ecological system. The Lotka-Volterra model proposed by Lotka (Carmichael & Lotka, 1926) and Volterra (1926) in 1926 is one of the fundamental models in ecology comprising two populations interacting at a time, one being the predator and another being the prey. So, the Lotka-Volterra model is also known as the predator-prey equations. The model describes the struggle for coexistence of two species ensuring the survival of both species for long term and hence paves the way for the abidance of the system.

The predator prey interaction is basically a process that creates disturbances to the system and under simple hypotheses the interaction of two species tends to generate periodic oscillations in reciprocal manner. The predator prey model is a pair of first order coupled ODE’s formulated by simple birth death process.

To specify the model, certain assumptions are made such as:

1. Only two species exist.

2. When predators are absent, prey population grows exponentially. Similarly predator population will starve and lead to exponential death in absence of prey.

3. Prey are primary source of food for predators and can be consumed in infinite quantity by predators.

4. In a homogeneous environment both populations can move randomly with-out any complexity. With these assumptions, the predator-prey populations are governed by the pair of equations: $$\begin{array}{c}\frac{dx}{dt}=\alpha x-\beta xy,\\ \frac{dy}{dt}=\delta xy-\gamma y,\end{array}$$ where x and y are the cardinality of prey and predator respectively. $\alpha , \beta , \gamma , \delta$ are positive real parameters signifying the interaction between the two species.

Recently, many researchers have studied the traditional Lotka-Volterra models with various modifications. A simple high-dimensional Lotka-Volterra model exhibiting spatiotemporal chaos in one spatial dimension is described by Sprott, Wildenberg, and Azizi (2005), Xiao and Ruan (2001b). Tiwana, Maqbool, and Mann (2017) studied the global dynamics of a ratio-dependent system. In which they use homotopy perturbation Laplace transform method to solve the fractional non-linear reaction diffusion system of Lotka-Volterra type differential equation. This can be considered as predator-prey System. Qualitative behaviour of a predator-prey system with nonmonotonic functional response with a series of bifurcations is discussed by Xiao and Ruan (2001a). Maiti, Sen, and Samanta (2016) analyzed the deterministic and stochastic prey–predator model with herd behaviour in both. Integro-differential equations for Lotka-Volterra model were derived by Anisiu (2014). The Holling type-II Lotka-Volterra predator-prey system with impulsive immigration of predator has been studied by Liu and Chen (2003). Fractional Lotka-Volterra population model using Haar wavelet and Adams-Bashforth-Moulton methods was given by Kumar, Kumar, Agarwal, & Samet (2020). Stability analysis for deterministic and stochastic fluctuations of a predator-prey model has been done by Addison (2017).

Recently, numerous models in biology (Dave, Khan, Purohit, & Suthar, 2021; Khan, Purohit, Dave, & Suthar, 2021; Mistry, Khan, & Suthar, 2020), and dynamics (Alaria, Khan, Suthar, & Kumar, 2019) can be modelled with the help of fractional order derivatives. In the past few years, many researchers have been established and applied numerous schemes to gain the solutions of fractional order differential equations such as Abeye, Ayalew, Suthar, Purohit, and Jangid (2022), Ramani, Khan, and Suthar (2019), and Ramani, Khan, Suthar, and Kumar (2022). Homotopy analysis method has been applied successfully by the researchers to find approximate solutions of fractional nonlinear partial differential equations (Agarwal, Yadav, Albalawi, Nisar, & Shefeeq, 2022; Hassani, Tabar, Nemati, Domairry, & Noori, 2011; Nassar, Revelli, & Bowman, 2011; Pareek, Gupta, Agarwal, & Suthar, 2021; Song & Zhang, 2007; Wu, Wang, & Liao, 2005; Zurigat, Momani, Odibat, & Alawneh, 2010; Yadav, Agarwal, Suthar & Purohit, 2022) as it is not easy to attain the exact solution of these equations. Also HAM has an advantage over other techniques to control the convergence region of the solution by choosing the auxiliary parameter arbitrarily.

This paper is organized as follows. In Sec. 2, we discussed some fractional calculus theory which has been used in the main findings. In Sec. 3, HAM is implemented to solve the fractional deterministic model of Lotka-Volterra type and analytic approximate solution is also found in the form of infinite series. In Sec. 4, the numerical analysis for fractional and auxiliary parameters has also been done. Finally, in Sec. 5 is concerned with the conclusion.

2. Basic definitions

In this part, we will review some fundamental properties of fractional calculus theory that will be useful in our work (Agarwal, Kritika, & Purohit, 2021; Agarwal, Kritika, Purohit, & Kumar, 2021; Dave et al., 2021; Ghanbari, Kumar, & Kumar, 2020; Kritika & Agarwal, 2020; Kumar, Kumar, Samet, Gómez-Aguilar, and Osman, 2020; Miller & Ross, 1993; Oldham & Spanier, 1974; Podlubny, 1999; Suthar, Purohit, & Araci, 2020; Veeresha, Prakasha, & Kumar, 2020):

Definition 2.1.

If $\aleph (x),x>0$ is a real valued function, then it is said to be in the space $C_{\mu },\mu \in \mathfrak{R}$ if $\exists$ $p>\mu$ s.t.: $$\aleph (x)=x^p{\aleph }_{1}x$$ where ${\aleph }_1(x)\in C[0,\infty \}.$

Definition 2.2.

If $\aleph (x),x>0$ is a real valued function, then it is said to be in the space $C_{\mu }^n,m\in N\cup \left\{0\right\},if{\aleph }^{(m)}\in C_{\mu }.$

Definition 2.3.

The Riemann-Liouville fractional integral operator of order $\propto \ge 0,$ for a function $\aleph \in C_{\mu },\mu \ge 1$ is $$\begin{array}{c}{J}^{\propto }\aleph \left(x\right)=\frac{1}{\Gamma (\propto )}{\int }_0^x\begin{array}{c}{\left(x-t\right)}^{\propto -1}\aleph \left(t\right)dt;(\propto >0,x>0),\end{array}\\ J^0\aleph \left(x\right)=\aleph (x).\end{array}$$

Which follows the properties: $$\begin{array}{c}{J}^{\propto }{J}^{\beta }\aleph \left(x\right)=J^{\propto +\beta }\aleph \left(x\right),\\ J^{\propto }{x}^{\beta }=\frac{\Gamma (\beta +1)}{\Gamma (\propto +\beta +1)}{x}^{\alpha +\beta }.\end{array}$$

Definition 2.4.

The Caputo’s sense fractional derivative of $\aleph \in C_{-1}^n$ is: $$D^{\propto }\aleph \left(t\right)=\{\begin{array}{c}\frac{1}{\Gamma \left(n-\propto \right)}{\int }_0^t{\left(t-\tau \right)}^{n-\alpha -1}{\aleph }^n\left(\tau \right)d\tau ,n-1<\alpha <n,n\in N^{*},\\ \frac{d^n}{d{t}^n}\aleph \left(t\right),\propto =n.\end{array}$$ and $$D^{\propto }K=0;K\mathrm{is}\mathrm{a}\mathrm{constant},$$ $$D^{\propto }{t}^{\beta }=\{\begin{array}{c}\frac{\Gamma \left(\beta +1\right)}{\Gamma \left(\beta -\propto +1\right)}{t}^{\beta -\alpha } \beta >\alpha -1,\\ 0,\beta \le \alpha -1.\end{array}$$

3. Homotopy analysis methodology for fractional nonlinear PDE’s

HAM for nonlinear systems can be explained by the following equation: (3.1) $$N_i[u_i(t)]=0,$$(3.1) where N_i and u_i are nonlinear operators and unknown functions respectively and t is the independent variables. By ignoring all boundary or initial condition, the zeroth-order deformation equation can be constructed as: (3.2) $$(1-p)L_i[{\varphi }_i(t,p)-u_{i0}(t)]=p{h}_i{H}_i(t)N_i[{\varphi }_i(t,p)],$$(3.2) where $p\in [0,1]$ is an embedding parameter, h_i $\ne$ 0 are auxiliary parameters, L_i are auxiliary linear operators, ${\varphi }_i(t,p)$ are unknown function, $u_{i0}$ (t) are an initial guesses of u_i (t) and H_i (t) $\ne 0$ denote nonzero auxiliary functions.

At p = 0 and p = 1, Eq. (3.2)(3.2) $$(1-p)L_i[{\varphi }_i(t,p)-u_{i0}(t)]=p{h}_i{H}_i(t)N_i[{\varphi }_i(t,p)],$$(3.2) reduced into (3.3) $${\varphi }_i(t,0)=u_{i0}(t),{\varphi }_i(t,1)=u_i(t).$$(3.3)

Thus as p increases from 0 to 1, the solution varies from the initial guess $u_{i0}(t)$ to the solution $u_i(t).$ Expanding ${\varphi }_i(t,p)$ in Taylor series with respect to p, $${\varphi }_i\left(t,p\right)=u_{i0}\left(t\right)+\sum _{m=1}^{\infty }{u}_{im}\left(t\right)p^m,$$ where (3.4) $$u_{im}\left(t\right)=\frac{1}{m!}\frac{{\partial }^m{\varphi }_i\left(t,p\right)}{\partial q^m}$$(3.4)

The convergence of the series in (3.4)(3.4) $$u_{im}\left(t\right)=\frac{1}{m!}\frac{{\partial }^m{\varphi }_i\left(t,p\right)}{\partial q^m}$$(3.4) depends upon the auxiliary parameters $h_i$ and the auxiliary function $s{H}_i(t).$ If it is convergent at $p=1,$ we have (3.5) $$u_i\left(t\right)=u_{i0}\left(t\right)+\sum _{m=1}^{\infty }{u}_{im}\left(t\right).$$(3.5) which is definitely one of the solutions of the nonlinear system considered in (3.1)(3.1) $$N_i[u_i(t)]=0,$$(3.1) , as proven by Liao (1997, 2004) and Goufo et al. (Doungmo Goufo, Kumar, & Mugisha, 2020).

Defining the vector $$\overrightarrow{u_i}=(u_{i0}\left(t\right),u_{i1}\left(t\right),\dots ,u_{in}\left(t\right)).$$

The mth order deformation equation can be written as (3.6) $$L_i[u_{im}\left(t\right)-{\chi }_m{u}_{i(m-1)}(t)]=h_i{H}_i\left(t\right)R_{im}\left[\overrightarrow{u_{i(m-1)}}(t)\right]$$(3.6)

Subject to the initial condition $$u_{im}\left(0\right)=0,$$ where $$\begin{array}{c}{R}_{im}\left[\overrightarrow{u_{i(m-1)}}(t)\right]=\frac{1}{(\mathrm{m}-1)!}\frac{{\partial }^{\mathrm{m}-1}{N}_i\left[{\varphi }_i\left(\mathrm{t},\mathrm{p}\right)\right]}{\partial {\mathrm{p}}^{\mathrm{m}-1}}\\ {\chi }_m=\{\begin{array}{cc}0,& m\le 1\\ 1,& m>1.\end{array}\end{array}$$

If we choose $L_i=D^{{\alpha }_i},$ then according to (3.6)(3.6) $$L_i[u_{im}\left(t\right)-{\chi }_m{u}_{i(m-1)}(t)]=h_i{H}_i\left(t\right)R_{im}\left[\overrightarrow{u_{i(m-1)}}(t)\right]$$(3.6) , we have $$J^{{\alpha }_i}{D}^{{\alpha }_i}\left[u_{im}\left(t\right)-{\chi }_m{u}_{i(m-1)}(t)\right]=h_i{J}^{{\alpha }_i}\left[H_i\left(t\right)R_{im}\left\{\overrightarrow{u_{i(m-1)}}\left(t\right)\right\}\right],$$ which further gives (3.7) $$u_{im}\left(t\right)={\chi }_m{u}_{i(m-1)}\left(t\right)+h_i{J}^{{\alpha }_i}\left[H_i\left(t\right)R_{im}\left\{\overrightarrow{u_{i(m-1)}}\left(t\right)\right\}\right],$$(3.7) subject to the initial condition: $$u_{im}\left(0\right)=0.$$

For the special case when α = 1, (3.6)(3.6) $$L_i[u_{im}\left(t\right)-{\chi }_m{u}_{i(m-1)}(t)]=h_i{H}_i\left(t\right)R_{im}\left[\overrightarrow{u_{i(m-1)}}(t)\right]$$(3.6) reduces to (3.8) $$u_{im}\left(t\right)={\chi }_m{u}_{i(m-1)}\left(t\right)+h_i{\int }_0^t\left[H_i\left(t\right)R_{im}\left\{\overrightarrow{u_{i(m-1)}}\left(t\right)\right\}\right]d\tau .$$(3.8)

4. Numerical solution of Lotka-Volterra model

Consider the Lotka-Volterra model of predator-prey coupled time fraction differential equations given by (4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) where $0<p,q\le 1,$ p and $q$ are the time fractional parameters for prey and predator equations respectively, where x and y are the cardinality of prey and predator respectively. $\alpha , \beta , \gamma , \delta$ are positive real parameters denoting the natural growth rate of prey in the absence of predation, predation impact coefficient for prey, natural death rate of predators in absence of prey and coefficient of efficiency of predation respectively.

In order to solve (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) using HAM, let the auxiliary linear operators $L_i=\frac{d}{dt},$ auxiliary functions $H_1(t)=H_2(t)=1$ and the initial guesses for the prey and predator population be $x_0(t)=80$ and $y_0(t)=30.$

Now, the homotopy for the system of Eq. (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) can be constructed as (4.2) $$\begin{array}{c}{R}_{1m}\left[\overrightarrow{x_{m-1}}(t)\right]=D^p{x}_{m-1}\left(t\right)-\alpha x_{m-1}\left(t\right)+\beta \sum _{i=0}^{m-1}{x}_i\left(t\right)y_{m-i-1}(t),\\ R_{2m}\left[\overrightarrow{y_{m-1}}(t)\right]=D^p{y}_{m-1}\left(t\right)-\delta \sum _{i=0}^{m-1}{x}_i\left(t\right)y_{m-i-1}(t)+\gamma y_{m-1}\left(t\right),\end{array}$$(4.2) and accordingly by HAM, we have (4.3) $$\begin{array}{c}{x}_m(\mathrm{t})={\chi }_m{x}_{m-1}\left(t\right)+h_1{\int }_0^t{R}_{1m}\left[\overrightarrow{x_{m-1}}(\tau )\right]d\tau ,\\ y_m(\mathrm{t})={\chi }_m{y}_{m-1}\left(t\right)+h_2{\int }_0^t{R}_{2m}\left[\overrightarrow{y_{m-1}}(\tau )\right]d\tau .\end{array}$$(4.3)

Solving by HAM, the first few terms of the series solution for (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) are as follows: (4.4) $$\begin{array}{c}{x}_0=80,y_0=30,\\ x_1=-80h_1\left(\alpha -30\beta \right)t,y_1=30h_2(\gamma -80\delta )t,\\ x_2=-80h_1\left(\alpha -30\beta \right)t+40h_1{}^2{\left(\alpha -30\beta \right)}^2{t}^2\\ +1200\beta h_1{h}_2\left(\gamma -80\delta \right)t^2-80h_1{}^2\left(\alpha -30\beta \right)\frac{t^{2-p}}{\Gamma (3-p)},\\ y_2=30h_2\left(\gamma -80\delta \right)t+15h_2{}^2{\left(\gamma -80\delta \right)}^2{t}^2\\ +1200\delta h_1{h}_2\left(\alpha -30\beta \right)t^2+30h_2{}^2\left(\gamma -80\delta \right)\frac{t^{2-q}}{\Gamma (3-q)},\\ x_3=-80h_1\left(\alpha -30\beta \right)t+\left\{80h_1{}^2{\left(\alpha -30\beta \right)}^2+2400\beta h_1{h}_2\left(\gamma -80\delta \right)\right\}{t}^2\\ +\{-40h_1{}^3{\left(\alpha -30\beta \right)}^3-3600\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\\ +1200\beta h_1{h}_2{}^2{\left(\gamma -80\delta \right)}^2+96000\beta \delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\}\frac{t^3}{3}\\ +\left\{-160h_1{}^2\left(\alpha -30\beta \right)\right\}\frac{t^{2-p}}{\Gamma (3-p)}\\ +\left\{160h_1{}^3{\left(\alpha -30\beta \right)}^2+2400\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\\ +\left\{-80h_1{}^3\left(\alpha -30\beta \right)\right\}\frac{t^{3-2p}}{\Gamma (4-2p)}+\left\{2400\beta h_1{h}_2{}^2\left(\gamma -80\delta \right)\right\}\frac{t^{3-q}}{\Gamma (4-q)},\\ y_3=30h_2\left(\gamma -80\delta \right)t+\left\{30h_2{}^2{\left(\gamma -80\delta \right)}^2+2400\delta h_1{h}_2\left(\alpha -30\beta \right)\right\}{t}^2\\ +\{15h_2{}^3{\left(\gamma -80\delta \right)}^3+3600h_1{h}_2{}^2\delta \left(\gamma -80\delta \right)\left(\alpha -30\beta \right)-1200\delta h_1{}^2{h}_2{\left(\alpha -30\beta \right)}^2\\ -36000\beta \delta h_1{h}_2{}^2\left(\gamma -80\delta \right)\}\frac{t^3}{3}+\left\{60h_2{}^2\left(\gamma -80\delta \right)\right\}\frac{t^{2-q}}{\Gamma (3-q)}\\ +\left\{60h_2{}^3{\left(\gamma -80\delta \right)}^2+2400\delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\\ +\left\{30h_2{}^3\left(\gamma -80\delta \right)\right\}\frac{t^{3-2q}}{\Gamma (4-2q)}+\left\{2400\delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\end{array}$$(4.4) and so on.

Now taking the auxiliary linear operators $L_1=D^p$ and $L_2=D^q$ for the system (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) , then the homotopy is written as $$\begin{array}{c}{x}_m(\mathrm{t})={\chi }_m{x}_{m-1}\left(t\right)+h_1{J}^p\left[R_{1m}\left(\overrightarrow{x_{m-1}}(\tau )\right)\right],\\ y_m(\mathrm{t})={\chi }_m{y}_{m-1}\left(t\right)+h_2{J}^q\left[R_{2m}\left(\overrightarrow{y_{m-1}}(\tau )\right)\right].\end{array}$$

For this case, we get the consecutive terms of the series solution as (4.5) $$\begin{array}{c}{x}_0=80,y_0=30,\\ x_1=-80h_1\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)},y_1=30h_2(\gamma -80\delta )\frac{t^q}{\Gamma (1+q)},\\ x_2=-80h_1\left(1+h_1\right)\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+80h_1{}^2{\left(\alpha -30\beta \right)}^2\frac{t^{2p}}{\Gamma (1+2p)}\\ +2400\beta h_1{h}_2\left(\gamma -80\delta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ y_2=30h_2\left(1+h_2\right)\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+30h_2{}^2{\left(\gamma -80\delta \right)}^2\frac{t^{2q}}{\Gamma (1+2q)}\\ +2400\delta h_1{h}_2\left(\alpha -30\beta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ x_3=-80h_1{\left(1+h_1\right)}^2\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+\left\{160h_1{}^2\left(1+h_1\right){\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p}}{\Gamma (1+2p)}\\ +\left\{-80h_1{}^3{\left(\alpha -30\beta \right)}^3\right\}\frac{t^{3p}}{\Gamma (1+3p)}+\left\{2400\beta h_1{h}_2\left(2+h_1+h_2\right)\left(\gamma -80\delta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{2400\beta h_1{h}_2{}^2{\left(\gamma -80\delta \right)}^2\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}+\left\{-2400\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{80\delta }{\left(\gamma -80\delta \right)}\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)},\\ y_3=30h_2{\left(1+h_2\right)}^2\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+\left\{60h_2{}^2\left(1+h_2\right){\left(\gamma -80\delta \right)}^2\right\}\frac{t^{2q}}{\Gamma (1+2q)}\\ +\left\{30h_2{}^3{\left(\gamma -80\delta \right)}^3\right\}\frac{t^{3q}}{\Gamma (1+3q)}+\left\{2400\delta h_1{h}_2\left(2+h_1+h_2\right)\left(\alpha -30\beta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{-2400\delta h_1{}^2{h}_2{\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)}+\left\{2400\delta h_1{h}_2{}^2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{30\beta }{\left(\alpha -30\beta \right)}\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}\end{array}$$(4.5)

and so on.

Here we have taken only first four terms of the infinite series to construct the numerical solution of (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) , but further terms can also be found to improve the solution.

The graphical results for the solutions obtained in (4.4)(4.4) $$\begin{array}{c}{x}_0=80,y_0=30,\\ x_1=-80h_1\left(\alpha -30\beta \right)t,y_1=30h_2(\gamma -80\delta )t,\\ x_2=-80h_1\left(\alpha -30\beta \right)t+40h_1{}^2{\left(\alpha -30\beta \right)}^2{t}^2\\ +1200\beta h_1{h}_2\left(\gamma -80\delta \right)t^2-80h_1{}^2\left(\alpha -30\beta \right)\frac{t^{2-p}}{\Gamma (3-p)},\\ y_2=30h_2\left(\gamma -80\delta \right)t+15h_2{}^2{\left(\gamma -80\delta \right)}^2{t}^2\\ +1200\delta h_1{h}_2\left(\alpha -30\beta \right)t^2+30h_2{}^2\left(\gamma -80\delta \right)\frac{t^{2-q}}{\Gamma (3-q)},\\ x_3=-80h_1\left(\alpha -30\beta \right)t+\left\{80h_1{}^2{\left(\alpha -30\beta \right)}^2+2400\beta h_1{h}_2\left(\gamma -80\delta \right)\right\}{t}^2\\ +\{-40h_1{}^3{\left(\alpha -30\beta \right)}^3-3600\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\\ +1200\beta h_1{h}_2{}^2{\left(\gamma -80\delta \right)}^2+96000\beta \delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\}\frac{t^3}{3}\\ +\left\{-160h_1{}^2\left(\alpha -30\beta \right)\right\}\frac{t^{2-p}}{\Gamma (3-p)}\\ +\left\{160h_1{}^3{\left(\alpha -30\beta \right)}^2+2400\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\\ +\left\{-80h_1{}^3\left(\alpha -30\beta \right)\right\}\frac{t^{3-2p}}{\Gamma (4-2p)}+\left\{2400\beta h_1{h}_2{}^2\left(\gamma -80\delta \right)\right\}\frac{t^{3-q}}{\Gamma (4-q)},\\ y_3=30h_2\left(\gamma -80\delta \right)t+\left\{30h_2{}^2{\left(\gamma -80\delta \right)}^2+2400\delta h_1{h}_2\left(\alpha -30\beta \right)\right\}{t}^2\\ +\{15h_2{}^3{\left(\gamma -80\delta \right)}^3+3600h_1{h}_2{}^2\delta \left(\gamma -80\delta \right)\left(\alpha -30\beta \right)-1200\delta h_1{}^2{h}_2{\left(\alpha -30\beta \right)}^2\\ -36000\beta \delta h_1{h}_2{}^2\left(\gamma -80\delta \right)\}\frac{t^3}{3}+\left\{60h_2{}^2\left(\gamma -80\delta \right)\right\}\frac{t^{2-q}}{\Gamma (3-q)}\\ +\left\{60h_2{}^3{\left(\gamma -80\delta \right)}^2+2400\delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\\ +\left\{30h_2{}^3\left(\gamma -80\delta \right)\right\}\frac{t^{3-2q}}{\Gamma (4-2q)}+\left\{2400\delta h_1{}^2{h}_2\left(\alpha -30\beta \right)\right\}\frac{t^{3-p}}{\Gamma (4-p)}\end{array}$$(4.4) and (4.5)(4.5) $$\begin{array}{c}{x}_0=80,y_0=30,\\ x_1=-80h_1\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)},y_1=30h_2(\gamma -80\delta )\frac{t^q}{\Gamma (1+q)},\\ x_2=-80h_1\left(1+h_1\right)\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+80h_1{}^2{\left(\alpha -30\beta \right)}^2\frac{t^{2p}}{\Gamma (1+2p)}\\ +2400\beta h_1{h}_2\left(\gamma -80\delta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ y_2=30h_2\left(1+h_2\right)\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+30h_2{}^2{\left(\gamma -80\delta \right)}^2\frac{t^{2q}}{\Gamma (1+2q)}\\ +2400\delta h_1{h}_2\left(\alpha -30\beta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ x_3=-80h_1{\left(1+h_1\right)}^2\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+\left\{160h_1{}^2\left(1+h_1\right){\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p}}{\Gamma (1+2p)}\\ +\left\{-80h_1{}^3{\left(\alpha -30\beta \right)}^3\right\}\frac{t^{3p}}{\Gamma (1+3p)}+\left\{2400\beta h_1{h}_2\left(2+h_1+h_2\right)\left(\gamma -80\delta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{2400\beta h_1{h}_2{}^2{\left(\gamma -80\delta \right)}^2\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}+\left\{-2400\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{80\delta }{\left(\gamma -80\delta \right)}\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)},\\ y_3=30h_2{\left(1+h_2\right)}^2\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+\left\{60h_2{}^2\left(1+h_2\right){\left(\gamma -80\delta \right)}^2\right\}\frac{t^{2q}}{\Gamma (1+2q)}\\ +\left\{30h_2{}^3{\left(\gamma -80\delta \right)}^3\right\}\frac{t^{3q}}{\Gamma (1+3q)}+\left\{2400\delta h_1{h}_2\left(2+h_1+h_2\right)\left(\alpha -30\beta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{-2400\delta h_1{}^2{h}_2{\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)}+\left\{2400\delta h_1{h}_2{}^2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{30\beta }{\left(\alpha -30\beta \right)}\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}\end{array}$$(4.5) of the system (4.1)(4.1) $$\begin{array}{c}{D}_t^{p}x=\alpha x-\beta xy,\\ D_t^{q}y=\delta xy-\gamma y,\end{array}$$(4.1) are illustrated through Figures 1–6 for various values of the fractional parameters p and q, auxiliary parameters h₁ and h₂ and for the choice of auxiliary linear operators L_i as $\frac{d}{dt}$ 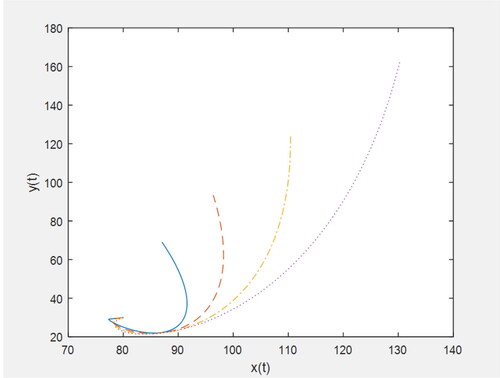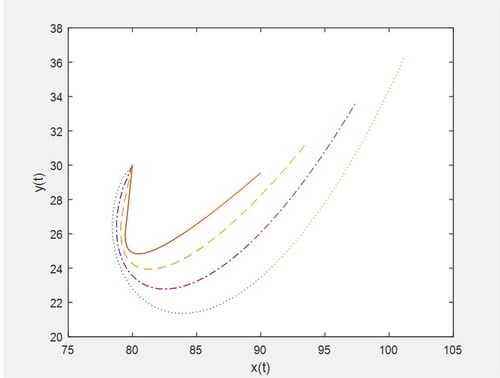or D^p and D^q respectively. Figures 7 and 8 depict the phase plots for (4.5)(4.5) $$\begin{array}{c}{x}_0=80,y_0=30,\\ x_1=-80h_1\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)},y_1=30h_2(\gamma -80\delta )\frac{t^q}{\Gamma (1+q)},\\ x_2=-80h_1\left(1+h_1\right)\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+80h_1{}^2{\left(\alpha -30\beta \right)}^2\frac{t^{2p}}{\Gamma (1+2p)}\\ +2400\beta h_1{h}_2\left(\gamma -80\delta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ y_2=30h_2\left(1+h_2\right)\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+30h_2{}^2{\left(\gamma -80\delta \right)}^2\frac{t^{2q}}{\Gamma (1+2q)}\\ +2400\delta h_1{h}_2\left(\alpha -30\beta \right)\frac{t^{p+q}}{\Gamma (1+p+q)},\\ x_3=-80h_1{\left(1+h_1\right)}^2\left(\alpha -30\beta \right)\frac{t^p}{\Gamma (1+p)}+\left\{160h_1{}^2\left(1+h_1\right){\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p}}{\Gamma (1+2p)}\\ +\left\{-80h_1{}^3{\left(\alpha -30\beta \right)}^3\right\}\frac{t^{3p}}{\Gamma (1+3p)}+\left\{2400\beta h_1{h}_2\left(2+h_1+h_2\right)\left(\gamma -80\delta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{2400\beta h_1{h}_2{}^2{\left(\gamma -80\delta \right)}^2\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}+\left\{-2400\beta h_1{}^2{h}_2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{80\delta }{\left(\gamma -80\delta \right)}\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)},\\ y_3=30h_2{\left(1+h_2\right)}^2\left(\gamma -80\delta \right)\frac{t^q}{\Gamma (1+q)}+\left\{60h_2{}^2\left(1+h_2\right){\left(\gamma -80\delta \right)}^2\right\}\frac{t^{2q}}{\Gamma (1+2q)}\\ +\left\{30h_2{}^3{\left(\gamma -80\delta \right)}^3\right\}\frac{t^{3q}}{\Gamma (1+3q)}+\left\{2400\delta h_1{h}_2\left(2+h_1+h_2\right)\left(\alpha -30\beta \right)\right\}\frac{t^{p+q}}{\Gamma (1+p+q)}\\ +\left\{-2400\delta h_1{}^2{h}_2{\left(\alpha -30\beta \right)}^2\right\}\frac{t^{2p+q}}{\Gamma (1+2p+q)}+\left\{2400\delta h_1{h}_2{}^2\left(\gamma -80\delta \right)\left(\alpha -30\beta \right)\right\}\\ \left\{1+\frac{\Gamma (1+p+q)}{\Gamma (1+p)\Gamma (1+q)}-\frac{30\beta }{\left(\alpha -30\beta \right)}\right\}\frac{t^{p+2q}}{\Gamma (1+p+2q)}\end{array}$$(4.5) for varying values of the p and q.

Figure 1. Plot for $L_i=\frac{d}{dt}$ when $p=q=1;$ solid line: $h_1=h_2=-1,$ dashed line: $h_1=-1.2,h_2=-1.2,$ dashed dotted line: $h_1=-1.4,h_2=-1.4.$

Figure 2. Plot for $L_i=\frac{d}{dt}$ when $p=0.7,q=0.9;$ solid line: $h_1=h_2=-1,$ dashed line: $h_1=-1.2,h_2=-1.2,$ dashed dotted line: $h_1=-1.4,h_2=-1.4.$

Figure 3. Plot for $L_1=D^p,L_2=D^q$ when $p=q=1;$ solid line: $h_1=h_2=-1,$ dashed line: $h_1=-1.2,h_2=-1.2,$ dashed dotted line: $h_1=-1.4,h_2=-1.4.$

Figure 4. Plot for $L_1=D^p,L_2=D^q$ when $p=0.7,q=0.9;$ solid line: $h_1=h_2=-1,$ dashed line: $h_1=-1.2,h_2=-1.2,$ dashed dotted line: $h_1=-1.4,h_2=-1.4.$

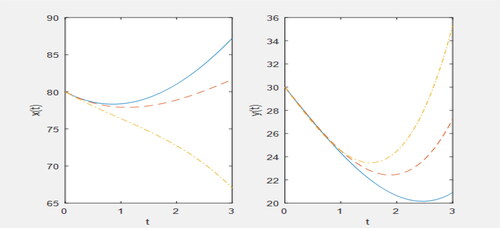
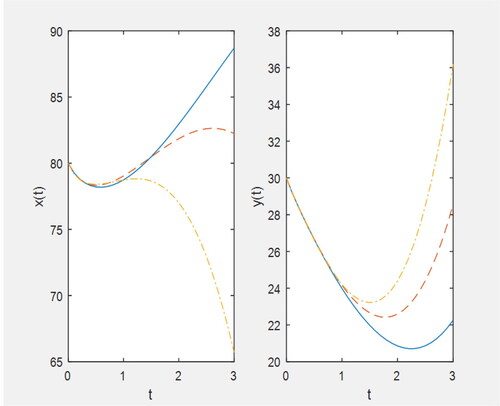
Figure 5. Plot for x(t) (i) for $L_1=\frac{d}{dt},$ (ii) for $L_1=D^p$ when $h_1=h_2=-1,q=0.9;$ solid line: p = 0.1, dashed line: p = 0.3, dashed dotted line: p = 0.5, dotted line: p = 0.7.

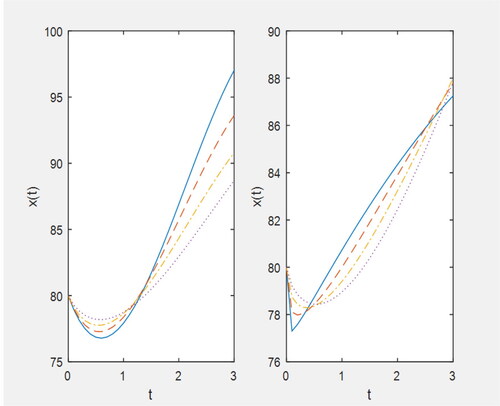
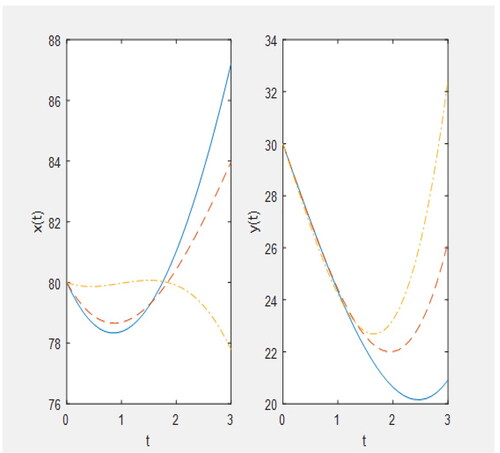
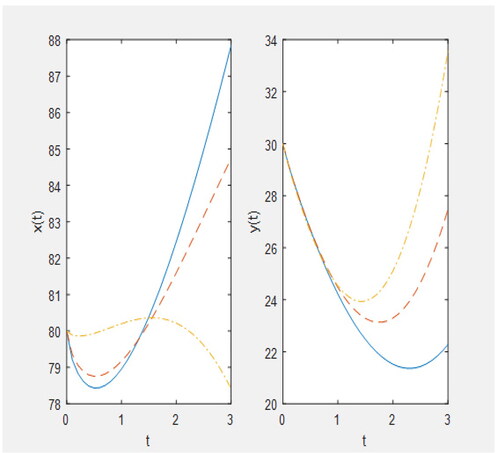
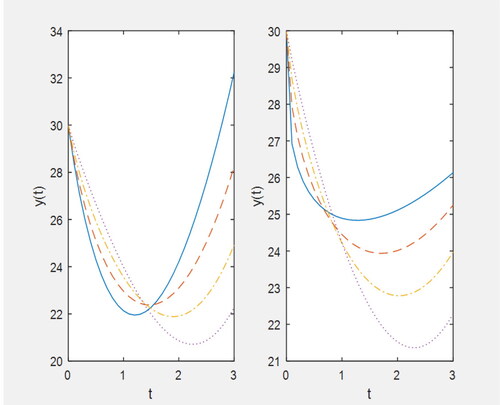
Figure 6. Plot for y(t) (i) for $L_2=\frac{d}{dt},$ (ii) for $L_2=D^q$ when $h_1=h_2=-1,p=0.7;$ solid line: q = 0.3, dashed line: q = 0.5, dashed dotted line: q = 0.7, dotted line: q = 0.9.

Figure 7. Plot for $L_1=D^p,L_2=D^q$ when $h_1=h_2=-1,q=0.9;$ solid line: p = 0.1, dashed line: p = 0.3, dashed dotted line: p = 0.5, dotted line: p = 0.7.

Figure 8. Plot for $L_1=D^p,L_2=D^q$ when $h_1=h_2=-1,p=0.7;$ solid line: q = 0.3, dashed line: q = 0.5, dashed dotted line: q = 0.7, dotted line: q = 0.9.

5. Concluding remark

1. Figures 1–2 and Figures 3–4 depict that for both the choices of auxiliary linear operators, decrease in the values of auxiliary parameters h₁ and h₂ shows the decay in mass concentration of prey species whereas that of predator shows a growth.

2. Figure 5 shows that for increase in the values of the fractional parameter p, prey population shows an increase for some time, although it decreases with time for different values of p but as the time goes on it shows the reverse trend i.e. greater values of p correspond to lesser values of prey population and it increases with the time t.

3. Figure 6 shows that for increase in the values of the fractional parameter q, predator population shows an increase for some time, although it decreases with time for different values of q but as the time goes on it shows the reverse trend i.e. greater values of q correspond to lesser values of predator population and it increases with the time t.

4. Figures 7 and 8 show the variation of predator population corresponding to the prey population for varying values of the fractional parameters p and q respectively.

5. These figures show that the mass concentration of prey increases and the same decreases for predator with the time t.

Authors’ contributions

The authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.

Acknowledgements

The authors are grateful to the editor and reviewers for their thorough review and comments, which contributed to improving this article.

Disclosure statement

The authors declare that they have no competing interests.