?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
This paper provides some methodological, didactical, and historiographical reflections on Egyptian pyramid volume formulas, responding to suggestions by Paul Shutler from 2009. These suggestions partly reiterate a historically documented proof by the Chinese Liu Hui (third century CE), although Lui Hui’s contribution was apparently unknown to Shutler. The latter came forward, in addition, with intuitive arguments which might have been used by the Egyptians to convince themselves of the correctness of their formula for the volume of the full pyramid. In a broad sense, the reflections in this paper may contribute to the use of history in the mathematical classroom. As a cautionary note: The paper is an abridged version of a longer manuscript that contains detailed explanations and discussions of historical secondary sources. Since the paper is somewhat outside the usual canon of mathematics historiography, I have deposited the longer manuscript on <arXiv.org>.
2020 Mathematics Subject Classification:
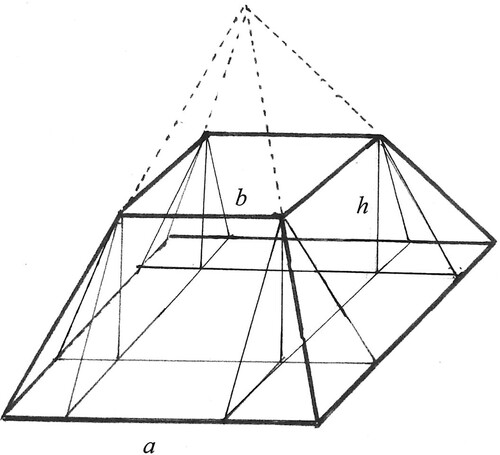
Egyptologists and historians of mathematics around 1930 (Struve, Gunn, Peet, Neugebauer, Thomas, Vogel etc.)Footnote1 did an admirable job in showing that problem 14 of the Moscow Papyrus (1850 BCE), found at the end of the nineteenth century, amounts to a general and exact calculation of the volume of a truncated pyramid with quadratic base (see ). Using modern algebraic terminology, the Egyptian procedure can be expressed by the following formula FT, where T stands for ‘truncated’:
(FT)
(FT) They were less successful in giving tentative explanations for how the Egyptians may have found the solution and what convinced them of its correctness.
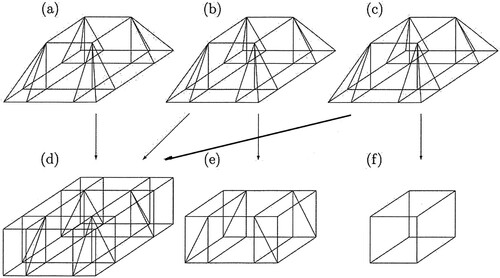
None of these works, to my knowledge, considered the ‘formula’ as expressing the rearrangement of three identical copies of the truncated pyramid (henceforth frustum, which is a general term for truncated solids) into three boxes although – in my opinion – the formula suggests this if one reads it as an average of three volumes. The only major problem during this rearrangement is to show that the volume of the 12 corner pyramids is equal to the volume of the four corner cuboids in the biggest of the resulting three boxes (see (d) in ). A few decades later, in the 1970s, historians of Chinese mathematics showed that such rearrangement was basically the method which Liu Hui had used in the third century CE in order to confirm an analogous ‘formula’ from the classical Nine Chapters of Chinese mathematics from the first millennium BCE.Footnote2 This method is expressed in Figure 2 from a paper by Paul Shutler (Citation2009), which stimulated this article.
Figure 2. From Shutler (Citation2009, 349). I have added the bold arrow from (c) to (d) to Shutler’s picture, replacing an erroneous arrow in Shutler which goes from (c) to (e).
The most authoritative modern textbook on the history of Egyptian mathematics contains only one passage directly related to the volume formula for the frustum:
There have been multiple attempts to explain how the Egyptian formula to calculate the volume of a truncated pyramid could have been achieved; some of these explanations use a clever modification of algebraic formulas—which were not used in Egyptian mathematics. Other explanations have tried to use practical experiences in form of woodworking. Another possibility would be the use of our knowledge of calculations of volumes of other objects from the hieratic mathematical texts. There are examples of calculations of the volumes of cylinders (e.g. papyrus Rhind, numbers 41 and 42) and a cube (papyrus Rhind, number 44). The underlying strategy for calculating their volumes is a multiplication of base and height. The procedure for calculating the volume of a truncated pyramid may be seen as a variation of that basic concept. Since the shape of the object indicates that a simple multiplication of the base and the height would result in a volume too big (i.e. that of the respective cuboid), a modification is put into place using three different ‘bases’ (the actual base, i.e. the square of the lower side), a rectangle made up of lower side and upper side, and the top area (a square of the upper side). To balance the sum of three areas (instead of one), they are then multiplied not by the height but by a third of the height. (Imhausen Citation2016, 75–76)
At the beginning of the quote, Imhausen reiterates a previous general remark from the introduction to her book, where she had critically alluded to several historians around 1930 and stated that by them several geometric problems were ‘phrased in anachronistic modern terminology … similar to our algebraic equations’ (Imhausen Citation2016, 5). At the end of this paper, I will come back to this justified criticism and will argue that this habit of some historians about 1930 led modern historians to scepticism with respect to any reasoning ‘to explain how the Egyptian formula to calculate the volume of a truncated pyramid could have been achieved.’
Mathematicians (Max Dehn and others) have shown that it requires ‘infinitesimal methods’ in the broadest sense to prove that the volume of a complete and symmetric pyramid is one third of the volume of the cuboid erected on the same square with the same height. This claim is, of course, a special case of the formula FT for the truncated pyramid with side length b = 0 for the top square. I allude to this in the title of my paper as the second, albeit implicit, Egyptian pyramid volume formula. However, this formula for the volume of the full pyramid can also be regarded as an axiom based on experience – practical engineering work on the pyramids or by weighing models, or ‘woodworking’ in the sense of Imhausen’s quote – and could thus hypothetically have been accepted by the Egyptians without proofFootnote4 if they were at all interested in justifications.
Although thus – strictly speaking – the proof of the ‘second formula’ can be separated from the dissection proof indicated in and its claim treated as a known fact, Paul Shutler in his paper of 2009 suggested, in addition, an intuitive proof which arguably was within the reach of Egyptian mathematical thinking. On this more below, but now back to .
Instead of the road taken by Liu Hui, and recently again by Shutler, historians around 1930 such as Gunn, Peet, and Neugebauer assumed the dissection of only one copy of the symmetrical frustum into nine parts – one central box (cuboid), four prisms and four asymmetrical corner pyramids – as a possible first step for the Egyptians to confirm ‘their formula’ FT. This dissection requires no algebraic manipulation because the volumes are represented by simple geometrical figures. In algebraic notation (which of course was not available to the Egyptians), this corresponds to the first line in the following formula, where the third term does not need to be interpreted yet as a volume formula for an asymmetric pyramid and can just be considered as an abbreviation for the volumes of the four asymmetric corner pyramids (TA stands for truncated, alternative):
(FTA)
(FTA) This is quite analogous to what is done with each of the three frustums in Shutler’s diagram (). But now the same historians assumed two further steps. First, one can intuitively – again without algebra – combine the first (1 + 4) = five volumes into a box with volume abh, which corresponds in above to the arrow from (b) to (e). The four asymmetric corner pyramids – here each designated by
– can then be easily assembled to form a symmetric (!) pyramid on a square with the area (a–b)2. These two further steps result in the final version of the equation above. The problem with this procedure of dissecting and recomposing one frustum is, however, that from now on a direct and intuitive way to the classical formula FT of the Moscow Papyrus is barred.Footnote5
I call formula FTA, which is equally as exact and general as FT, the ‘alternative volume-formula’ of the truncated pyramid. However, it cannot be called an ‘Egyptian formula’ because it is only assumed by historians as being plausible to the Egyptians. Gunn, Peet, and Neugebauer now further assumed that the Egyptians would have seen the need to ‘simplify’ FTA: for example by taking out the common factor h which leads to
This elementary arithmetic simplification for avoiding repeated multiplication, which is reminiscent of the algorithm in the Moscow Papyrus and thus of FT, was according to the authors ‘well known to the Egyptians’ (Gunn and Peet Citation1929, 182), also documented in other texts as in the Rhind Papyrus. This operation of taking out a common factor is also assumed by Imhausen in the quote above and cannot be disputed in its legitimacy. However, one can dispute its usefulness or expediency.
First one may dispute that the previous version of the formula FTA – before taking out the common factor h – is any more complicated than the classical formula FT. Gunn and Peet refer to the ease of memorizing the latter formula. Here one might object that this feeling may result from its algebraic symmetry and its similarity with the expression for (a + b)2 = (a2 +2ab + b2) which we may associate with it, based on our algebraic knowledge. Above all, however, the classical formula FT is much more ‘intuitive’ in the sense of relating to averages of areas or volumes, as indicated in the quote from Imhausen above. By way of contrast, the area ab + (a–b)2 in the ‘simplified’ form of FTA has no visible relation to the intuitive upper and lower bounds of areas for the base of the frustum, which can be seen in
in FT.
The ‘historians around 1930’ now tried to find a way from formula FTA to the classical volume formula FT for the truncated pyramid, which is in the Moscow Papyrus. Of course, none of those historians was so naive as to simply replace (a–b)2 in the formula FTA by a2 – 2ab + b2 which would lead directly to FT. Instead, they fell back on searching – without appeal to either two or three-dimensional intuition – for a base area derivable from FTA which, when multiplied by the height h, would produce exactly the desired formula FT. In doing so, these historians, in my opinion, succumbed to an axiomatic, deductive habit, acquired from Euclid, of initially viewing three-dimensional geometric problems as being based on and developed from plane geometry, a habit which can sometimes obstruct an original and intuitive approach that would make more pedagogical sense. The habit described could be considered a kind of ‘geometric algebra’ in a slightly generalized sense compared to the well-known historiographic discussion,Footnote6 namely as an unintuitive manipulation with plane figures. In any case, the possible intuitive interpretation of formula FT as a transformation of three identical frustums is thereby lost.Footnote7
As remarked before, both formulas, the classical and the alternative, have to rely on the fact that the volume of a full symmetric pyramid can be considered to be exactly one third of the volume of a box with the same height h and the same base.
Here the brilliant idea of Paul Shutler comes into play. He realizes that in the original numerical example of the Moscow Papyrus the side of the top square is half of the side of the bottom square (a = 4, b = 2). But this entails that the missing top pyramid VP in is congruent with the symmetric pyramid composed of the four asymmetric corner pyramids. At the same time, the completed pyramid with height 2h and a = 2b has eight times the volume of the top pyramid which is ‘similar’ – in a very intuitive and simple sense which does not require formal definition – to the full pyramid. This follows from simple intuitive arguments (which Shutler does not provide) such as approximately filling the two pyramids with the same number of identical cubes and then diminishing the sizes of the cubes indefinitely. This results in two independent ‘equations’ – understood as pure geometric identities – from which the volume formula for the full pyramid follows.
In some more detail: twice the volume of the top pyramid VP plus the remaining parallelepiped box hab equal in volume eight times the top pyramid VP. Thus the box has the same volume as six times the top pyramid. Thus 6VP = hab = 2hb2, since a = 2b. This means that the volume of a pyramid VP with base b2 is always equal to b2 because b can be arbitrarily chosen.
Shutler now seems to assume that the choice of the numbers for a and b in the Moscow Papyrus points to the fact that the Egyptians used exactly this argument to convince themselves of the correctness of the volume formula for the full symmetric pyramid. Be that as it may, Shutler’s idea seems to me a very fruitful speculation, one which can be used with profit in mathematics teaching.Footnote8 It may thus contribute to the use of history in mathematical education.Footnote9 Shutler’s proposal could be called ‘exact intuition’ as opposed to the ‘inexact’ one which is conveyed by the classical formula FT, as explained above. In any case, this proof method can be easily made rigorous by using fundamental notions of modern mathematics.
If the Egyptians should indeed have been impressed by the intuitiveness of their classical formula – as Imhausen seems to assume in her quote – and may even have had means – as we assumed further above – to convince themselves of its validity, the question still remains how they may have found the formula in the first place.
In fact, it comes as a kind of surprise that the three copies of the truncated pyramid produce exactly three simple boxes ha2, hab, and hb2, whose volume can be easily calculated. One probably has to take into account the practical context both in Egypt and China. Playing with models might have been encouraged or even been triggered by the ‘mathematical idea’ that dissecting exactly three copies of the frustum would in any case guarantee the production of simple volumes because the 12 corner pyramids would then equal 4 cuboids in volume. But the final result, the small number of only three simple boxes, was in a way ‘coincidental’. The resulting ‘symmetry’ and relative ‘simplicity’ of the formula FT are in my opinion not predictable. Admittedly, this is reminiscent of the typical unpredictability of formulas resulting from manipulations in algebra, and in this very restricted sense the Egyptians may have possessed some ‘algebraic thinking’, although performed with models (mentally or physically) and certainly without symbols. This is the core of what I consider the most convincing hypothetical way how the formula FT both in the Moscow Papyrus and in the Chinese Nine Chapters may have been found originally.
Although modern historians of Egyptian mathematics acknowledge – as we have seen – the intuitive potential of the classical formula FT, they do not seem to have considered manipulating with several copies of the frustum as a starting point for a possible Egyptian method. It seems to me that the Chinese proof method, discovered only in the 1970s (Wagner Citation1979), could stimulate a discussion whether the Egyptians might have used some similar argument 2000 years earlier. The authoritative account of Egyptian mathematics discussed above (Imhausen Citation2016) does not mention the example of Chinese mathematics (or other mathematical cultures such as the Indian) at all. Shutler, who is not a historian of mathematics, did not refer to the Chinese method either, although he may have known it subconsciously. The reason for the reluctance of modern Egyptologists and historians of Egyptian mathematics to use historical comparison in this sense seems to me to lie both in the scarcity of documentary source material and in the described methodological recklessness of the historians around 1930. The latter’s attempts at a hypothetical reconstruction of an Egyptian proof can even be called ‘presentist’, namely as inspired by Euclid (1,500 years after the Egyptians), and partly also by modern, algebraic thinking. Since such a ‘presentist’ view of history, later taken to extremes by Van der Waerden (Citation1983), among others, is now discredited, increased methodological caution has probably set in among some modern historians. As a result, however, in my opinion, an opportunity to exploit the great intuitive and pedagogical potential of the possible Egyptian and the actual Chinese procedure of pyramid truncation has been lost. With all due methodological caution, I believe that a discussion of a hypothetical Egyptian proof can be justified. This is valid particularly today, when such discussion can be based on the prominent historical comparative example of Liu Hui, who, like the Egyptians, had no algebraic methods, as we understand them, at his disposal. Of course, it must be emphasized that such a methodological and pedagogical discussion cannot solve the problem of what the actual procedure of the ancient Egyptians was and whether they had any desire for the justification of their formulas.
Acknowledgments
I am grateful to the following colleagues and friends for reading earlier versions of this manuscript and giving helpful advice: June Barrow-Green (London), Reinhard Bölling (Berlin), Karine Chemla (Paris), Joseph Dauben (New York), Simon Goodchild (Kristiansand), Christopher Hollings (Oxford), Jesper Lützen (Copenhagen), Nathan Sidoli (Tokyo), and Donald Wagner (Copenhagen). I thank the editor of BJHM for supporting this publication which is somewhat on the border between history, methodology, and pedagogy.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Notes
1 I call them in this paper summarily ‘historians around 1930’, being aware that among them were Egyptologists and mathematicians with different aims and competences. Imhausen refers – apparently with some critical intent – to several of these works in footnote 21 of her book (Imhausen Citation2016, 5).
2 In the full manuscript (Siegmund-Schultze Citation2022) I revisit Lui Hui’s proof, but I will not do so here. The proof is presented and commented on in detail in (Wagner Citation1979) and (Chemla and Guo Citation2004, 387–395, 817–818.)
3 Because the factor h/3 is applied at the end of the algorithm expressed by formula FT and therefore here written in the beginning, the interpretations as an average of area or volume seem equally plausible. In the Chinese version of the formula, the factor 1/3 is applied separately at the very end of the algorithm. This makes its interpretation as an average of volumes very likely from the outset.
4 Throughout this paper, I consider ‘proof’ generally as a rational argument which contributes to the conviction of correctness of some mathematical claim and is historically variable. See Chemla (Citation2012).
5 Interestingly, Liu Hui derives formula FTA additionally, but he is content with it and does not use it at all to derive the classical formula FT once again.
6 In the course of this debate one of the most famous historians of ancient mathematics, Otto Neugebauer, was at times accused of unduly insinuating a hidden algebraic agenda among ancient mathematicians. See the most recent contribution (Blåsjö Citation2016), which recognizes the dangers of projecting modern algebraic methodology on the past but also acknowledges the relative merits of such procedure in the historical reconstruction of ancient geometry.
7 More details in (Siegmund-Schultze Citation2022).
8 The famous historian Otto Neugebauer, who started his historical work with Egyptian mathematics before 1930, assumed without any explanation that the Egyptians were in possession of Cavalieri’s principle which would have allowed them to compare the volumes of symmetric and oblique pyramids (Neugebauer Citation1934, 128). Shutler in his ‘speculation’ assumes much less because his argument is based on two symmetrical (!) pyramids which are in a very intuitive sense ‘similar’.
9 The present author goes as far as accepting even an occasional use of counterfactual history, which is of course not the case in the present example because we cannot rule out that the Egyptians used exactly this argument.
Bibliography
- Blåsjö, Viktor, ‘In defence of geometrical algebra’, Archive for History of Exact Sciences, 70 (2016), 325–359.
- Chemla, Karine (ed), The history of mathematical proofs in ancient traditions, Cambridge: Cambridge University Press, 2012.
- Chemla, Karine, and Guo, Shuchun (eds), Les neuf chapitres: Le classique mathématique de la chine ancienne et ses commentaires. Édition critique bilingue traduite, présentée et annotée, Paris: Dunod, 2004.
- Gunn, Battiscombe, and Peet, Thomas E, ‘Four geometrical problems from the Moscow mathematical papyrus’, Journal of Egyptian Archaeology, 15 (1929), 167–185.
- Imhausen, Annette, Egyptian mathematics. A contextual history, Princeton: Princeton University Press, 2016.
- Neugebauer, Otto, Vorgriechische Mathematik, Berlin: Springer, 1934.
- Shutler, Paul, ‘The problem of the pyramid or Egyptian mathematics from a postmodern perspective’, International Journal of Mathematical Education in Science and Technology, 40 (2009), 341–352.
- Siegmund-Schultze, Reinhard, Intuitive, didactically useful, and historically possible proofs for the two Egyptian pyramid volume “formulas” (1850 BCE): thoughts on the border between history and didactics of mathematics, 2022, 39pp. http://arxiv.org/abs/2207.04427.
- Waerden, B L v d, Geometry and algebra in ancient civilizations, Berlin: Springer, 1983.
- Wagner, Donald B, ‘An ancient Chinese derivation of the volume of a pyramid: Liu Hui, third century A.D.’, Historia Mathematica, 6 (1979), 164–188.