Estimation of variance of the difference-cum-ratio-type exponential estimator in simple random sampling

ABSTRACT

In this article, we have suggested a class of estimators for the estimation of the population variance of the variable of interest. The proposed estimators used some certain known information of the auxiliary variable, such as kurtosis, coefficient of variation, and the minimum and maximum values. The properties of the suggested class of estimators such as the bias and mean squared error (MSE) are obtained up to the first order of approximation. In order to check the performances of the estimators and to verify the theoretical results, we conducted a simulation study. The results of the simulation study show that the proposed class of estimators have lower MSE than other existing estimators. This holds for all simulation scenarios. In the application part, we used data from Statistical Bureau of Pakistan, and from the Textbook of Cochran, which also confirms that the suggested class of estimators is more efficient than the usual unbiased variance estimator, ratio estimator, traditional regression estimator, and other existing estimators in survey literature.

KEYWORDS:

• Study variable
• auxiliary information
• variance estimation
• minimum and maximum values
• bias
• MSE

1. Introduction

The purpose of survey sampling is to get accurate information about the characteristics of the population for improving the efficiency of the estimators under study at the lowest costs, less time and human efforts (for more details, see Yang et al. (2020)). In several populations, there has been a few extreme values and to estimate the unknown population parameters without including this information is very sensitive. In which case, the results will be underestimated or overestimated. To solve this issue, it is important to use this information in estimating the population parameters. Isaki (1983), Bahl and Tuteja (1991), Upadhyaya and Singh (1999), Kadilar and Cingi (2006), Dubey and Sharma (2008), H. Singh and Chandra (2008), Shabbir and Gupta (2010), H. P. Singh and Solanki (2013), and Yadav et al. (2015) have all suggested some wider classes of estimators for estimating finite population variance. Consider a finite population $U=\left(U_1,U_2,U_3,\dots ,U_N\right)$ of size $N$ units. Let $y_i$ and $x_i$ be the values of the study variable $Y$ and the auxiliary variable $X$ for the $ith$ units respectively. Let $\bar{Y}=\left(1/N\right){\sum }_{i=1}^N{Y}_i$ and $\bar{X}=\left(1/N\right){\sum }_{i=1}^N{X}_i$ be the population mean of the study and the auxiliary variable, respectively. It is further assumed that $S_y^2=\left(1/N-1\right){\sum }_{i=1}^N{\left(Y_i-\bar{Y}\right)}^2$ and $S_x^2=\left(1/N-1\right){\sum }_{i=1}^N{\left(X_i-\bar{X}\right)}^2$ be the population variances of the study as well as auxiliary variable, respectively.

To estimate the unknown population parameter $\bar{Y}$, we select a random sample of size $n$ units from the population by using simple random sampling without replacement (SRSWOR). Let $\bar{y}=\left(1/n\right){\sum }_{i=1}^n{y}_i$ and $\bar{x}=\left(1/n\right){\sum }_{i=1}^n{x}_i$ be the sample means of the study and the auxiliary variables, respectively, and their corresponding sample variances are ${\hat{S}}_y^2=\left(1/n-1\right){\sum }_{i=1}^n{\left(y_i-\bar{y}\right)}^2$ and ${\hat{S}}_x^2=\left(1/n-1\right){\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2$, respectively.

To find the bias and MSE for different estimators, we define the following terms. Let $e_0=\left(\frac{s_y^2-S_y^2}{S_y^2}\right)$, $e_1=\left(\frac{s_x^2-S_x^2}{S_x^2}\right)$ and $e_2=\left(\frac{\bar{x}-\bar{X}}{\bar{X}}\right)$ such that $E\left(e_i\right)=0$ for i = 0, 1, 2.$E\left(e_0^2\right)=\theta {\lambda }_{40}^{\ast },E\left(e_1^2\right)=\theta {\lambda }_{04}^{\ast },E\left(e_2^2\right)=\theta C_x^2,E\left(e_0{e}_1\right)=\theta {\lambda }_{22}^{\ast },E\left(e_0{e}_2\right)=\theta C_x{\lambda }_{21}$

$E\left(e_1{e}_2\right)=\theta C_x{\lambda }_{03},$

where ${\lambda }_{40}^{\ast }=({\lambda }_{40}-1)$, ${\lambda }_{04}^{\ast }=({\lambda }_{04}-1)$, ${\lambda }_{22}^{\ast }=({\lambda }_{22}-1)$, $\theta =\left(\frac{1}{n}-\frac{1}{N}\right)$. Also ${\lambda }_{rs}=\frac{{\mu }_{rs}}{{\mu }_{20}^{r/2}{\mu }_{02}^{s/2}}$, where ${\mu }_{rs}=\frac{{\sum }_{i=1}^N{\left(Y_i-\bar{Y}\right)}^r{\left(X_i-\bar{X}\right)}^s}{N-1}$. Here ${\lambda }_{40}={\beta }_{2(y)}$ and ${\lambda }_{04}={\beta }_{2(x)}$ are the population coefficients of kurtosis.

The usual variance estimator of ${\hat{S}}_y^2=s_y^2$ [1] for population variance is given by

(1.1) $Var({\hat{S}}_y^2)=\theta S_y^4{\lambda }_{40}^{\ast }.$(1.1)

Isaki (1983) suggested a ratio-type estimator for the variance of the study variable $Y$, which is denoted by ${\hat{S}}_R^2$ [2], and is given by

(1.2) ${\hat{S}}_R^2=s_y^2\left(\frac{S_x^2}{s_x^2}\right),$(1.2)

Expressions for bias and MSE of ${\hat{S}}_R^2$, in sample random sampling (SRS) are given by

(1.3) $Bias\left({\hat{S}}_R^2\right)\cong \theta S_y^4\left({\lambda }_{04}^{\ast }-{\lambda }_{22}^{\ast }\right),$(1.3)

and

(1.4) $MSE\left({\hat{S}}_R^2\right)\cong \theta S_y^4\left({\lambda }_{40}^{\ast }+{\lambda }_{04}^{\ast }-2{\lambda }_{22}^{\ast }\right).$(1.4)

The classical regression estimator ${\hat{S}}_{lr}^2$ [3] in SRS is given by

(1.5) ${\hat{S}}_{lr}^2=s_y^2+b_{(s_y^2,s_x^2)}\left(S_x^2-s_x^2\right),$(1.5)

where $b_{(s_y^2,s_x^2)}=\frac{s_y^2{\hat{\lambda }}_{22}^{\ast }}{s_x^2{\hat{\lambda }}_{04}^{\ast }}$ is the sample regression coefficient. The MSE of the estimator ${\hat{S}}_{lr}^2$, is given by

(1.6) $MSE\left({\hat{S}}_{lr}^2\right)\cong \theta S_y^4{\lambda }_{40}^{\ast }\left(1-{\rho }^{\ast 2}\right),$(1.6)

where

(1.7) ${\rho }^{\ast }=\frac{{\lambda }_{22}^{\ast }}{\sqrt{{\lambda }_{40}^{\ast }}\sqrt{{\lambda }_{04}^{\ast }}}$(1.7)

.

Bahl and Tuteja (1991) suggested an exponential ratio-type estimator for the population variance of the study variable $Y$, which is denoted by ${\hat{S}}_{BT}^2$ [4] and is given by:

(1.8) ${\hat{S}}_{BT}^2=s_y^{2}exp\left(\frac{S_x^2-s_x^2}{S_x^2+s_x^2}\right),$(1.8)

Expressions for bias and MSE respectively of ${\hat{S}}_{BT}^2$, are given by

(1.9) $Bias\left({\hat{S}}_{BT}^2\right)\cong \frac{1}{2}\theta S_y^2\left(\frac{3{\lambda }_{04}^{\ast }}{4}-{\lambda }_{22}^{\ast }\right),$(1.9)

and

(1.10) $MSE\left({\hat{S}}_{BT}^2\right)\cong \theta S_y^4\left({\lambda }_{40}^{\ast }+\frac{{\lambda }_{04}^{\ast }}{4}-{\lambda }_{22}^{\ast }\right).$(1.10)

Upadhyaya and Singh (1999) proposed a ratio-type estimator ${\hat{S}}_{US}^2$ [5], that uses the kurtosis of an auxiliary variable in SRS, given by

(1.11) ${\hat{S}}_{US}^2=s_y^2\left(\frac{S_x^2+{\lambda }_{04}}{s_x^2+{\lambda }_{04}}\right),$(1.11)

Expressions for bias and MSE respectively of ${\hat{S}}_{US}^2$, are given by

(1.12) $Bias\left({\hat{S}}_{US}^2\right)\cong \theta S_y^2{g}_0\left(g_0{\lambda }_{04}^{\ast }-{\lambda }_{22}^{\ast }\right),$(1.12)

and

(1.13) $MSE\left({\hat{S}}_{US}^2\right)\cong \theta S_y^4\left({\lambda }_{40}^{\ast }+g_0^2{\lambda }_{04}^{\ast }-2g_0{\lambda }_{22}^{\ast }\right),$(1.13)

where

(1.14) $g_0=\frac{S_x^2}{S_x^2+{\lambda }_{04}}$(1.14)

.

Kadilar and Cingi (2006) suggested a class of ratio estimators ${\hat{S}}_{KCi}^2$ [6–8] which are given by

(1.15) ${\hat{S}}_{KC1}^2=s_y^2\left(\frac{S_x^2+C_x}{s_x^2+C_x}\right),$(1.15)

(1.16) ${\hat{S}}_{KC2}^2=s_y^2\left(\frac{{\lambda }_{04}{S}_x^2+C_x}{{\lambda }_{04}{s}_x^2+C_x}\right),$(1.16)

(1.17) ${\hat{S}}_{KC3}^2=s_y^2\left(\frac{C_x{S}_x^2+{\lambda }_{04}}{C_x{s}_x^2+{\lambda }_{04}}\right),$(1.17)

where $C_x=\frac{S_x}{\bar{X}}$ is the population coefficient of variation.

Expressions for bias and MSE’s respectively of ${\hat{S}}_{KCi}^2(i=1,2,3)$, in SRS are given by

(1.18) $Bias\left({\hat{S}}_{KCi}^2\right)\cong \theta S_y^2{g}_i\left(g_i{\lambda }_{04}^{\ast }-{\lambda }_{22}^{\ast }\right),$(1.18)

and

(1.19) $MSE\left({\hat{S}}_{KCi}^2\right)\cong \theta S_y^4\left({\lambda }_{40}^{\ast }+g_i^2{\lambda }_{04}^{\ast }-2g_i{\lambda }_{22}^{\ast }\right),$(1.19)

where

(1.20) $g_1=\frac{S_x^2}{S_x^2+C_x},g_2=\frac{{\lambda }_{04}{S}_x^2}{{\lambda }_{04}{S}_x^2+C_x},g_3=\frac{C_x{S}_x^2}{C_x{S}_x^2+{\lambda }_{04}}.$(1.20)

2. Proposed estimators

Motivated by Daraz et al. (2018), we proposed an improved class of estimators for estimating the finite population variance $S_y^2$ using certain known population parameters under simple random sampling scheme. The proposed estimator is given by

(2.1) ${\hat{S}}_D^2=\left[k_1{s}_y^2{\left(\frac{S_x^2}{s_x^2}\right)}^{{\alpha }_1}+k_2\left(\bar{X}-\bar{x}\right){\left(\frac{S_x^2}{s_x^2}\right)}^{{\alpha }_2}\right]exp\left(\frac{a_1(s_x^2-S_x^2)}{a_1(s_x^2+S_x^2)+2b_1}\right),$(2.1)

where $k_1$ and $k_2$ are the unknown constants whose values are to be determined such that the MSE’s are minimum, $a_1$ and $b_1$ are the parameters of the auxiliary variables. Also, ${\alpha }_1$ and ${\alpha }_2$ are the scalar quantities which contain the values (0, −1, 1) from (2.1) we can generate the different classes of proposed estimator which are given in Table 1.

Table 1. Some classes of the proposed estimator

Subsets of the proposed estimator ${\hat{S}}_D^2$	${\alpha }_1$	${\alpha }_2$	$a_1$	$b_1$
[9] ${\hat{S}}_{D1}^2=\left[k_1{s}_y^2\left(\frac{S_x^2}{s_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{s_x^2}{S_x^2}\right)\right]L$	$1$	$-1$	$-{\beta }_{2(x)}$
[10] ${\hat{S}}_{D2}^2=\left[k_1{s}_y^2\left(\frac{S_x^2}{s_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\right]L$	$1$	$0$	$x_M-x_m$
[11] ${\hat{S}}_{D3}^2=\left[k_1{s}_y^2\left(\frac{s_x^2}{S_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{s_x^2}{S_x^2}\right)\right]L$	$-1$	$-1$	$x_M-x_m$
[12] ${\hat{S}}_{D4}^2=\left[k_1{s}_y^2+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{S_x^2}{s_x^2}\right)\right]L$	$0$	$1$	$x_M-x_m$
[13] ${\hat{S}}_{D5}^2=\left[k_1{s}_y^2+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{s_x^2}{S_x^2}\right)\right]L$	$0$	$-1$	${\beta }_{2(x)}$
[14] ${\hat{S}}_{D6}^2=\left[k_1{s}_y^2\left(\frac{S_x^2}{s_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{S_x^2}{s_x^2}\right)\right]L$	$1$	$1$	$x_M-x_m$
[15] ${\hat{S}}_{D7}^2=\left[k_1{s}_y^2\left(\frac{s_x^2}{S_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\left(\frac{S_x^2}{s_x^2}\right)\right]L$	$-1$	$1$	$-c_x$
[16] ${\hat{S}}_{D8}^2=\left[k_1{s}_y^2\left(\frac{s_x^2}{S_x^2}\right)+k_2\left(\bar{X}-\bar{x}\right)\right]L$	$-1$	$0$	$c_x$

where

(2.2) $L=exp\left(\frac{a_1(s_x^2-S_x^2)}{a_1(s_x^2+S_x^2)+2b_1}\right)$(2.2)

.

Properties of the proposed estimator

Rewriting (2.1) in term of errors, we have

(2.2) $\begin{array}{r}{\hat{S}}_D^2=\left[k_1{S}_y^2\left(1+e_0\right){\left(1+e_1\right)}^{-{\alpha }_1}-k_2\bar{X}{e}_2{\left(1+e_1\right)}^{-{\alpha }_2}\right]\\ exp\left[\frac{-g_4{e}_1}{2}{\left(1+\frac{g_4}{2}{e}_1\right)}^{-1}\right]\end{array}$(2.2)

where

(2.3) $g_4=\frac{a_1{S}_x^2}{a_1{S}_x^2+b_1}$(2.3)

.

By using Taylor series up to the first order of approximation, we have

(2.3) $\begin{array}{c}{\hat{S}}_D^2-S_y^2\cong -S_y^2+k_1{S}_y^2\left[1+e_0-e_1\left({\alpha }_1+\frac{g_4}{2}\right)+e_1^2\left(\frac{{\alpha }_1{g}_4}{2}+\frac{3g_4^2}{8}+\frac{{\alpha }_1\left({\alpha }_1+1\right)}{2}\right)\right.\left.-e_0{e}_1\left({\alpha }_1+\frac{g_4}{2}\right)\right]\\ -k_2\bar{X}\left[e_2-e_1{e}_2\left({\alpha }_2+\frac{g_4}{2}\right)\right]\end{array}$(2.3)

Using (2.3), the bias of ${\hat{S}}_D^2$, is given by

(2.4) $Bias\left({\hat{S}}_D^2\right)\cong -\left[S_y^2-k_1{S}_y^{2}D-k_{2}G\right],$(2.4)

where $D=\left[1+\theta \left\{{\lambda }_{04}^{\ast }\left(\frac{3g_4^2+4{\alpha }_1\left(g_4+{\alpha }_1+1\right)}{8}\right)-\left.{\lambda }_{22}^{\ast }\left(\frac{{\alpha }_1+g_4}{2}\right)\right\}\right.\right]$, and $G=\theta S_x{\lambda }_{03}\left(\frac{{\alpha }_2+g_4}{2}\right)$. By squaring and taking expectation on both sides of Equation (2.3)(2.3) $\begin{array}{c}{\hat{S}}_D^2-S_y^2\cong -S_y^2+k_1{S}_y^2\left[1+e_0-e_1\left({\alpha }_1+\frac{g_4}{2}\right)+e_1^2\left(\frac{{\alpha }_1{g}_4}{2}+\frac{3g_4^2}{8}+\frac{{\alpha }_1\left({\alpha }_1+1\right)}{2}\right)\right.\left.-e_0{e}_1\left({\alpha }_1+\frac{g_4}{2}\right)\right]\\ -k_2\bar{X}\left[e_2-e_1{e}_2\left({\alpha }_2+\frac{g_4}{2}\right)\right]\end{array}$(2.3) , we get the mean squared error by using the first order of approximation, which is given by

(2.5) $MSE\left({\hat{S}}_D^2\right)\cong \left[S_y^4+k_1^2{S}_y^{4}A+k_2^{2}B-2k_1{S}_y^{4}D-2k_2{S}_y^{2}G+2k_1{k}_2{S}_y^{2}F\right],$(2.5)

where

$A=\left.\left[1+\theta \left\{{\lambda }_{40}^{\ast }+{\lambda }_{04}^{\ast }\left\{{\left({\alpha }_1+\frac{g_4}{2}\right)}^2+\left.\left({\alpha }_1{g}_4+\frac{3g_4^2}{4}+\frac{{\alpha }_1\left({\alpha }_1+1\right)}{2}\right)\right\}\right.\right.\right.-\left.2{\lambda }_{22}^{\ast }\left(2{\alpha }_1+g_4\right)\right\}\right]$

,

$B=\theta S_x^2$, and $F=\theta S_x\left[{\lambda }_{03}({\alpha }_1+{\alpha }_2+g_4)-{\lambda }_{21}\right]$.

The optimum values of $k_1$ and $k_2$ obtained by minimizing (2.5) are $k_{1\left(opt\right)}=\frac{BD-FG}{AB-F^2}$, and $k_{2\left(opt\right)}=\frac{S_y^2\left(AG-DF\right)}{AB-F^2}$. By substituting the optimum values of $k_1$ and $k_2$ in (2.5), we get the minimum MSE of ${\hat{S}}_D^2$, which is given below:

(2.6) $MSE{\left({\hat{S}}_D^2\right)}_{min}\cong S_y^4\left[1-\frac{\left(A{G}^2+B{D}^2-2DFG\right)}{AB-F^2}\right].$(2.6)

3. Mathematical comparison

In this section, we compare the suggested class of estimator ${\hat{S}}_D^2$ with the existing estimators ${\hat{S}}_y^2,{\hat{S}}_R^2,{\hat{S}}_{lr}^2,{\hat{S}}_{BT}^2,{\hat{S}}_{US}^2$, and ${\hat{S}}_{KCi}^2$.

Condition (i): By (1.1) and (2.6), $Var({\hat{S}}_y^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta {\lambda }_{40}^{\ast }+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

Condition (ii): By (1.4) and (2.6), $MSE({\hat{S}}_R^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta \left({\lambda }_{40}^{\ast }+{\lambda }_{04}^{\ast }-2{\lambda }_{22}^{\ast }\right)+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

Condition (iii): By (1.6) and (2.6), $MSE({\hat{S}}_{lr}^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta {\lambda }_{40}^{\ast }\left(1-{\rho }^{\ast 2}\right)+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

Condition (iv): By (1.9) and (2.6), $MSE({\hat{S}}_{BT}^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta \left({\lambda }_{40}^{\ast }+\frac{{\lambda }_{04}^{\ast }}{4}-{\lambda }_{22}^{\ast }\right)+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

Condition (v): By (1.12) and (2.6), $MSE({\hat{S}}_{US}^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta \left({\lambda }_{40}^{\ast }+g_0^2{\lambda }_{04}^{\ast }-2g_0{\lambda }_{22}^{\ast }\right)+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

Condition (vi): By (1.17) and (2.6), $MSE({\hat{S}}_{KCi}^2)>MSE{\left({\hat{S}}_D^2\right)}_{min}$ if

$\theta \left({\lambda }_{40}^{\ast }+g_i^2{\lambda }_{04}^{\ast }-2g_i{\lambda }_{22}^{\ast }\right)+\left(\frac{A{G}^2+B{D}^2-2DFG}{AB-F^2}\right)>1.$

4. Simulation study

In order to verify the theoretical results in Section 3, we have conducted a simulation study by using the idea from Agarwal et al. (2012). We generated six different artificial populations of the auxiliary variable $X$ by using the following probability distributions.

• $X\sim Exponential(\lambda =3)$ and $X\sim Exponential(\lambda =7)$, • $X\sim Uniform(b_3=0,b_4=1)$ and $X\sim Uniform(b_3=3,b_4=5)$,

• $X\sim Gamma({\alpha }_3=4,{\alpha }_4=6)$ and $X\sim Gamma({\alpha }_3=8,{\alpha }_4=10)$.

After that, the study variable $Y$is computed as $Y=r_{yx}\times X+e$, taking $r_{yx}=0.80$, where $r_{yx}$ is the correlation coefficient between the study and the auxiliary variables and $e\sim N(0,1)$ is the error term.

We considered the following steps in R-Software to obtain the MSE’s of the proposed class of estimators:

Step 1: In the first step, we generated a population of size 1000 using a certain type of probability distributions.

Step 2: We obtained population total, minimum and maximum values of the auxiliary variable from Step 1. We also computed the optimum values of the unknown constants of the proposed estimator.

Step 3: We considered different sample sizes for each population to generate the samples using SRSWOR.

Step 4: For each sample size, the values of bias’s and MSE’s are computed for all the estimators considered in this paper.

Step 5: The process in Step 3 and Step 4 is repeated 50,000 times and the results for artificial populations are reported in Table 2, whereas the results of the real data sets are summarized in Table 3.

Table 2. Mean squared error (MSE) of the estimators using the artificial populations

Estimator	$X\sim Exp(3)$	$X\sim Exp(7)$	$X\sim Uni(0,1)$	$X\sim Uni(3,5)$	$X\sim Gam(4,6)$	$X\sim Gam(8,10)$
[1] ${\hat{S}}_y^2$	1.10e-3	9.70e-4	9.00e-4	1.40e-3	2.66e-2	1.10e-3
[2] ${\hat{S}}_R^2$	8.00e-4	8.80e-4	8.00e-4	1.20e-3	2.19e-2	1.00e-3
[3] ${\hat{S}}_{lr}^2$	8.00e-4	7.70e-4	7.00e-4	1.10e-3	2.16e-2	1.00e-3
[4] ${\hat{S}}_{BT}^2$	7.00e-4	7.40e-4	7.00e-4	1.10e-3	2.16e-2	1.00e-3
[5] ${\hat{S}}_{US}^2$	7.00e-4	7.50e-4	7.00e-4	1.10e-3	2.20e-2	1.00e-3
[6] ${\hat{S}}_{KC1}^2$	7.00e-4	7.10e-4	7.00e-4	1.00e-3	2.12e-2	1.00e-3
[7] ${\hat{S}}_{KC2}^2$	7.00e-4	7.10e-4	7.00e-4	1.10e-3	2.14e-2	1.00e-3
[8] ${\hat{S}}_{KC3}^2$	7.00e-4	7.20e-4	7.00e-4	1.00e-3	2.17e-2	9.00e-4
[9] ${\hat{S}}_{D1}^2$	2.00e-4	1.40e-4	2.00e-4	2.60e-4	3.80e-3	1.00e-4
[10] ${\hat{S}}_{D2}^2$	1.00e-4	1.00e-4	1.00e-4	1.00e-4	1.30e-3	5.00e-5
[11] ${\hat{S}}_{D3}^2$	2.40e-4	1.50e-4	1.20e-4	1.50e-4	3.50e-3	1.00e-4
[12] ${\hat{S}}_{D4}^2$	2.00e-4	1.60e-4	1.70e-4	2.00e-4	3.70e-3	1.00e-4
[13] ${\hat{S}}_{D5}^2$	2.50e-4	2.00e-4	2.00e-4	3.00e-4	4.20e-3	1.00e-4
[14] ${\hat{S}}_{D6}^2$	2.50e-4	2.00e-4	2.00e-4	2.70e-4	5.30e-3	1.60e-4
[15] ${\hat{S}}_{D7}^2$	1.20e-4	1.00e-4	1.40e-4	2.00e-4	2.70e-3	1.00e-4
[16] ${\hat{S}}_{D8}^2$	2.00e-5	2.00e-5	3.00e-5	4.00e-5	6.00e-4	2.00e-5

Table 3. Mean squared error (MSE) of the estimators using empirical data sets

Estimator	MSE: Data 1	MSE: Data 2	MSE: Data 3
[1] ${\hat{S}}_y^2$	1.21e+21	1.13e+21	8140.74
[2] ${\hat{S}}_R^2$	1.42e+21	1.40e+21	5702.73
[3] ${\hat{S}}_{lr}^2$	1.20e+21	1.13e+21	5667.55
[4] ${\hat{S}}_{BT}^2$	1.28e+21	1.19e+21	6442.13
[5] ${\hat{S}}_{US}^2$	1.40e+21	1.40e+21	5712.85
[6] ${\hat{S}}_{KC1}^2$	1.42e+21	1.40e+21	5703.41
[7] ${\hat{S}}_{KC2}^2$	1.42e+21	1.40e+21	5703.06
[8] ${\hat{S}}_{KC3}^2$	1.42e+21	1.40e+21	5785.88
[9] ${\hat{S}}_{D1}^2$	3.79e+20	2.09e+20	5401.90
[10] ${\hat{S}}_{D2}^2$	3.74e+20	5.21e+20	5084.03
[11] ${\hat{S}}_{D3}^2$	5.94e+20	5.60e+20	4759.47
[12] ${\hat{S}}_{D4}^2$	5.52e+20	3.11e+20	4340.05
[13] ${\hat{S}}_{D5}^2$	5.42e+20	4.74e+20	4233.81
[14] ${\hat{S}}_{D6}^2$	5.01e+20	3.01e+20	3594.18
[15] ${\hat{S}}_{D7}^2$	4.57e+20	7.33e+19	3068.23
[16] ${\hat{S}}_{D8}^2$	1.99e+19	2.85e+19	510.23

Finally, the MSE’s of the estimators over all replications are obtained by using the following formula. $MSE({\hat{S}}_k^2{)}_{min}=\frac{{\sum }_{g=1}^{50000}{\left({\hat{S}}_k^2-S_y^2\right)}^2}{50000}$, for $k=R,lr,BT,US,KCi,D1,D2,\dots ,D8$.

Figure 1. Graphical display of the MSE’s results of the estimators using the artificial data

Note: The vertical line of the figures shows the MSE’s of the estimators, while the horizontal line indicates the corresponding estimators. For easiness, we denote the estimators by different numbers starting from 1 to 16. For more details, see Table 2. Source: Own computations.

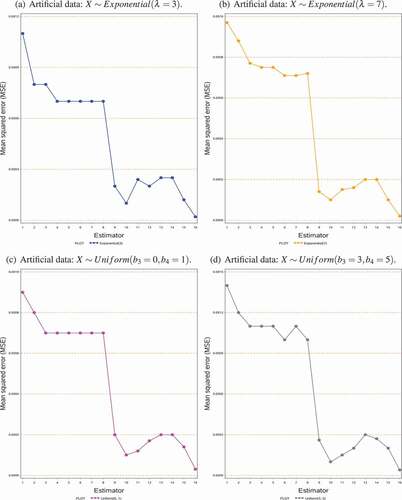
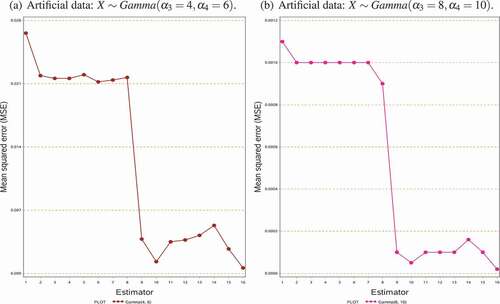
Figure 2. Graphical display of the MSE’s results of the estimators using the artificial data

Note: The vertical line of the figures shows the MSE’s of the estimators, while the horizontal line indicates the corresponding estimators. For easiness, we denote the estimators by different numbers starting from 1 to 16. For more details. see Table 2. Source: Own computations.

5. Numerical examples

To check the performances of the suggested class of estimators, we used three real data sets to compare the MSE’s of different estimators. The description and summary statistics are given by

Data 1. (Bureau of Statistics (2013), p. 135)

$Y$: Total number of students enrolls in 2012,

$X$: Total number of government primary and secondary schools for boys and girls 2012.

The summary statistics are given below:

$\begin{array}{c}N=36,n=15,\bar{Y}=148718.70,\bar{X}=1054.39,S_y=182315.10,S_x=402.61,\\ X_M=2370,X_m=388,C_x=0.38,C_y=1.23,{\lambda }_{40}=2365,{\lambda }_{04}=4698,{\lambda }_{03}=4697,\\ {\lambda }_{21}=4698,{\lambda }_{22}=8975,{\rho }_{yx}=\mathrm{0.18.}\end{array}$

Data 2. (Bureau of Statistics (2013), p. 226)

$Y$: Employment level in 2012 by divisions,

$X$: Number of registered factories in 2012 by divisions.

The summary statistics are given below:

$\begin{array}{c}N=36,n=15,\bar{Y}=52432.86,\bar{X}=335.78,S_y=178201.10,S_x=451.14,\\ X_M=2055,X_m=24,C_x=1.34,C_y=3.3986,{\rho }_{yx}=0.39,{\lambda }_{40}=2365,\\ {\lambda }_{04}=4698,{\lambda }_{03}=4697,{\lambda }_{21}=4698,{\lambda }_{22}=8975.\end{array}$

.

Data 3. ((Cochran (1963), p. 24)

$Y$: Food cost of families employment,

$X$: Weekly income of families.

The summary statistics are given below:

$\begin{array}{c}N=33,n=5,\bar{Y}=27.49,\bar{X}=72.55,S_y=10.13,S_x=10.58,X_M=95,\\ X_m=58,C_x=0.15,C_y=0.37,{\rho }_{yx}=0.25,{\lambda }_{40}=5.55,{\lambda }_{04}=2.08,{\lambda }_{03}=0.51,\\ {\lambda }_{21}=0.54,{\lambda }_{22}=\mathrm{2.22.}\end{array}$

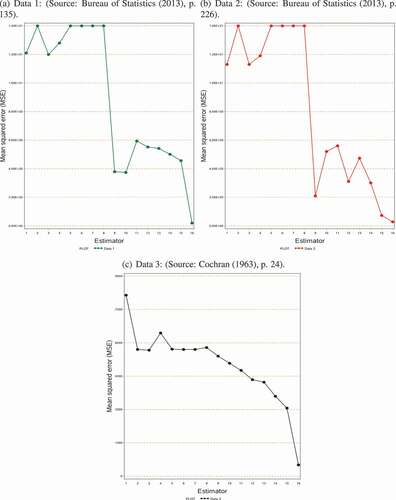
Figure 3. Graphical display of the MSE’s results of the estimators using the empirical data

Note: The vertical line of the Figures shows the MSE’s of the estimators, while the horizontal line indicates the corresponding estimators. For easiness, we denote the estimators by different numbers starting from 1 to 16. For more details, see Table 3. Source: Own computations.

6. Conclusion

In this paper, we proposed a class of estimators for estimating the population variance of the study variable using some known information of the auxiliary variable. The properties of the proposed class of estimators are compared with other existing estimators. For this purpose, we reported some theoretical conditions in Section 3 under which the proposed estimators are more efficient than the existing estimators. These theoretical conditions are verified through the help of a simulation study and some empirical data sets. MSE’s results of various estimators over the simulation setup are demonstrated in Table 2. In comparing the MSE’s of the estimators, it is clear from the table that the proposed class of estimators performs the best over the cited existing estimators. The MSE’s results of various estimators in Table 2 are plotted in Figures 1 and 2 which demonstrates that the MSE’s of the purposed class of estimators are significantly smaller than the MSE’s of other estimators. Similar results are obtained from the empirical data, which also confirms the theoretical results in Section 3. The empirical results are displayed in Table 3, which is then graphically shown in Figure 3. Hence, based on our simulation results as well as through empirical results, we observed that the proposed class of estimators ${\hat{S}}_{Di}^2(i=9,10,11,\dots ,16)$ are more efficient than the other considered estimators. Among the suggested class of estimators, ${\hat{S}}_{D8}^2$ is preferable because of its least MSE.

PUBLIC INTEREST STATEMENT

In this article, we have suggested a class of estimators for the estimation of the population variance by using the maximum and minimum values of independent variable. In order to check the performance of the estimators and to verify the theoretical results we conducted a simulation study from different distribution and also used the data sets from real life application and display it graphically which confirmed that the suggested class of estimator is more efficient than the existent estimators because it’s least mean squared errors.

Acknowledgment

This work was supported by NSFC of China with grant [12071329]. We are very thankful to the two unknown referees, and the editor for their insightful comments and suggestions which greatly improved this paper.

Disclosure statement

The authors declare that there is no conflict of interests regarding the publication of this article.

Additional information

Notes on contributors

Umer Daraz

Umer Daraz received his M.Phil degree in Survey Sampling from Quaid-i-Azam University, Islamabad, Pakistan in 2016. He is currently pursuing his PhD degree under the supervision of Prof. Tang Yu at Soochow University, Suzhou, China. His research interests lie in the survey sampling, design experiment and combination design.

Mursala Khan

Mursala Khan got his Doctorate degree from Free University Berlin, Germany. His field of specialization is survey sampling. Currently, he is working as an assistant professor in the Department of Mathematics and Statistics, Riphah International University, Islamabad, Pakistan.