Stokeslet parallèle entre deux disques rigides antidérapants positionnés de manière coaxiale : une approche aux équations intégrales duales

RÉSUMÉ

Les interactions hydrodynamiques induites par le confinement des particules colloïdales sont d’un intérêt de longue date. Cependant, les effets des géométries de confinement partiellement étendues ont reçu peu d’attention malgré leur applicabilité potentielle dans la manipulation des particules à travers des dispositifs microfluidiques. Nous élucidons comment l’hydrodynamique d’une microparticule colloïdale est altérée lorsqu’elle est confinée entre deux parois de taille finie. La microparticule a été modélisée par une force ponctuelle ou Stokelet, tandis que la finitude des confinements a été modélisée par deux disques circulaires de rayon fini. Nous rapportons les résultats d’une théorie semi-analytique basée sur une formulation intégrale duale qui nous permet d’analyser le problème basé sur une règle de quadrature unidimensionnelle au lieu d’effectuer des simulations numériques tridimensionnelles complètes. Nous démontrons l’existence de tourbillons de recirculation asymétriques dans le domaine fluide délimité par les deux disques. Notre analyse révèle que ces tourbillons ne se forment que lorsque la taille des substrats de confinement dépasse une certaine limite. La compréhension approfondie des structures d’écoulement et de leur dépendance à la taille du confinement peut potentiellement aider à concevoir de nouveaux dispositifs microfluidiques et à obtenir un contrôle avancé sur les propriétés d’écoulement en ajustant l’étendue des substrats enveloppants.

ABSTRACT

The hydrodynamic interactions induced by the confinement of colloidal particles have been of interest for a long time. However, the effects of partially extended containment geometries have received little attention despite their potential applicability in the manipulation of particles through microfluidic devices. We elucidate how the hydrodynamics of a colloidal microparticle is altered when it is confined between two walls of finite size. The microparticle was modeled by a point force or Stokeslet, while the finitude of the confinements was modeled by two circular discs of finite radius. We report the results of a semi-analytical theory based on a dual integral formulation that allows us to analyze the problem based on a one-dimensional quadrature rule instead of performing full three-dimensional numerical simulations. We demonstrate the existence of asymmetric recirculating vortices in the fluid domain delimited by the two disks. Our analysis reveals that these vortices only form when the size of the confining substrates exceeds a certain limit. In-depth understanding of flow structures and their dependence on containment size can potentially help design new microfluidic devices and gain advanced control over flow properties by adjusting the extent of confining substrates.

MOTS CLÉS:

• Interactions hydrodynamiques
• écoulement de Stokes
• mobilité hydrodynamique
• écoulements près des confinements
• écoulements visqueux
• équations intégrales

KEYWORDS:

• Hydrodynamic interactions
• Stokes flow
• hydrodynamic mobility
• flows near confinements
• viscous flows
• integral equations

1. Introduction

Les interactions hydrodynamiques à médiation fluide entre les particules colloïdales dans un milieu solvant sous confinement sont omniprésentes dans la nature et trouvent des applications dans divers processus industriels et technologiques (Graham, 2011 ; Martínez-Pedrero & Tierno, 2018 ; Tsori, 2020). Une compréhension approfondie de l’effet du confinement sur la dynamique et la rhéologie des suspensions colloïdales est d’une importance primordiale dans la conception et le développement de systèmes microfluidiques (Driscoll & Delmotte, 2019). Des notables exemples incluent la manipulation de particules/cellules dans les puces microfluidiques (Laumann et al., 2019 ; Nilsson et al., 2009 ; Shen et al., 2016 ; S. Zhang et al., 2020), l’analyse de séparation et de génotypage de l’ADN dans des canaux nano-capillaires (Kan et al., 2004 ; Wang et al., 2008 ; N. Zhang et al., 1999), et le sondage de structures complexes dans des mesures de microscopie à force atomique (AFM; François et al., 2009, 2008). Au cours des dernières décennies, d’énormes efforts de recherche ont été consacrés à la révélation du comportement des écoulements en suspension de particules dans des confinements étroits (Puertas et al., 2015).

Aux petites échelles de longueur et de temps, les fluides en écoulement sont régis par l’hydrodynamique à faible nombre de Reynolds, tant que les forces visqueuses dominent les forces d’inertie. Dans ces situations, une description complète des interactions mutuelles entre les particules en suspension dans un milieu visqueux est fournie par les mobilités hydrodynamiques (Kim & Karrila, 2013) qui relient les vitesses des particules aux forces exercées sur elles. De même, les particules interagissent hydrodynamiquement avec des confinements qui influencent les écoulements fluides induits. Cet effet se traduit par des expressions modifiées de la mobilité hydrodynamique. Des expressions analytiques des fonctions de mobilité sont tabulées pour divers types de confinements géométriques, par exemple, dans le manuel classique de Happel et Brenner (1983). Jusqu’à présent, les résultats analytiques disponibles incluent la solution pour la mobilité hydrodynamique et le mouvement brownien d’une particule se déposant près d’une paroi plane rigide (Bevan & Prieve, 2000 ; Franosch et al., 2011 ; Holmqvist et al., 2007 ; Hsu & Ganatos, 1989 ; Lisicki, 2015 ; Lisicki et al., 2012, 2014 ; Padding & Briels, 2010; Pagonabarraga et al., 1998 ; Rogers et al., 2012), une interface avec un glissement partiel (Felderhof, 2012 ; Lauga & Squires, 2005), une interface recouverte de surfactant (Blawzdziewicz, Cristini et al., 1999 ; Blawzdziewicz, Wajnryb et al., 1999 ; Shaik & Ardekani, 2017), une surface rugueuse (Kurzthaler et al., 2020), une membrane élastique soumise au cisaillement et/ou flexion (Bertin, 2021 ; Bertin et al., 2021 ; Bickel, 2006, 2007, 2014 ; Daddi-Moussa-Ider & Gekle, 2016, 2018 ; Daddi-Moussa-Ider et al., 2016a ; Daddi-Moussa-Ider, Lisicki, Gekle et al., 2018 ; Daddi-Moussa-Ider, Rallabandi et al., 2018 ; Hoell et al., 2019; Rallabandi et al., 2018, 2017; Saintyves et al., 2016 ; Salez & Mahadevan, 2015 ; Z. Zhang et al., 2020), ou une surface séparant deux liquides non miscibles entre eux (Fulford & Blake, 1983; Wang & Huang, 2014).

Dans un travail fondateur, le mouvement à faible nombre de Reynolds d’une particule colloïdale se déplaçant dans un canal délimité par deux plaques infiniment étendues a été examiné par Faxén (1921). Dans sa thèse de doctorat à l’université de Uppsala en Suède, Faxén a fourni des expressions perturbatives de la mobilité translationnelle pour le mouvement parallèle aux deux parois lorsque la particule se déplace dans le plan médian du canal ou dans un plan situé à une distance d’un quart de la largeur du canal (Happel & Brenner, 1983). Une solution exacte pour le mouvement arbitraire d’une particule ponctuelle se déplaçant dans un canal a été obtenue plus tard par Liron & Mochon (1976) en utilisant la technique d’images. La même méthode a été utilisée pour dériver la solution fondamentale dans un film liquide afin d’examiner l’hydrodynamique des micro-organismes (Mathijssen et al., 2016). De même, le mouvement arbitraire d’une particule vraiment étendue dans un canal à fente a été étudié en utilisant l’expansion multipolaire (Bhattacharya & Blawzdziewicz, 2002 ; Swan & Brady, 2010) ou via des techniques numériques (Ganatos et al., 1980 ; Gentile et al., 2015 ; Lee et al., 2018). Les prédictions théoriques ont été vérifiées en utilisant l’imagerie directe (Dufresne et al., 2001), la diffusion dynamique de la lumière (Lobry & Ostrowsky, 1996), ainsi que la microscopie vidéo (Faucheux & Libchaber, 1994) en combinaison avec des pincettes optiques (Lin et al., 2000 ; Tränkle et al., 2016).

Dans la présente contribution, nous étudions les caractéristiques d’écoulement induit par une force ponctuelle située le long de l’axe central entre deux disques positionnés coaxialement. La force est dirigée parallèlement aux surfaces des disques de confinement. En raison de l’asymétrie dans la direction du mouvement par rapport à l’axe central commun des disques, le champ d’écoulement devient de nature tridimensionnelle. Ainsi, la présente analyse va au-delà des caractéristiques du cas d’une force ponctuelle axisymétrique présenté précédemment (Daddi-Moussa-Ider, Sprenger et al., 2020). Nous décrivons d’abord en détail le problème physique étudié. Par la suite, le problème hydrodynamique est formulé en introduisant les équations régissant le mouvement des fluides ainsi que les conditions aux limites sous-jacentes. Nous adoptons une technique semi-analytique basée sur l’approche aux équations intégrales duales pour résoudre le problème des valeurs limites mixtes dérivé de la situation physique complexe en cours. Les résultats ainsi obtenus sont validés par des simulations 3D par éléments finis. Il a été constaté qu’un emplacement de décalage vertical de la force ponctuelle par rapport au centre géométrique du système et une variation de la taille du disque peuvent donner lieu à une multitude de caractéristiques uniques dans le champ d’écoulement ainsi qu’à la mobilité en translation d’une particule ponctuelle. En raison de la linéarité de l’écoulement de Stokes, une superposition linéaire des champs d’écoulement provenant du mouvement d’une force ponctuelle perpendiculaire et parallèle aux disques permet de prédire ses caractéristiques le long d’une direction arbitraire dans l’espace entre les deux disques.

2. Formulation mathématique

Comme présenté ci-dessus, nous examinons l’écoulement de fluide à faible nombre de Reynolds induit par une singularité de Stokeslet agissant tangente aux surfaces de deux disques rigides de même rayon $R$ positionnés coaxialement. Les disques sont situés à une distance $H$ l’un de l’autre, dans les plans $z=-H/2$ et $z=H/2$ du repère cartésien, voir Figure 1 pour une illustration schématique du système. De plus, les disques sont supposés être infiniment minces. Plus précisément, on considère la situation dans laquelle le Stokeslet est situé sur l’axe passant par les centres des disques positionnés coaxialement, décrit ici par l’axe $z$. On suppose que l’écoulement préserve le volume du fluide, et on note par $\eta$ la viscosité dynamique du fluide newtonien environnant remplissant tout l’espace.

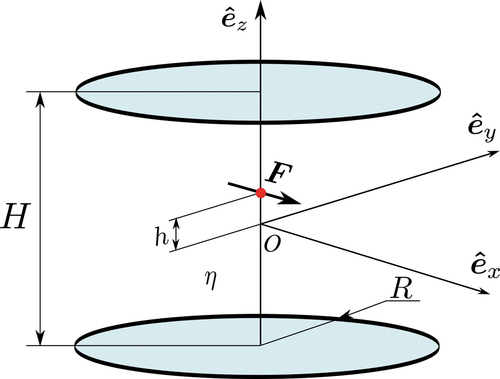
Figure 1. Description schématique montrant deux disques de rayon $R$ et de séparation $H$ positionnés coaxialement, et une singularité de force ponctuelle (Stokeslet) agissant entre eux à une hauteur $h$ au-dessus du point central coïncidant avec l’origine du système de coordonnés $O$. Ce Stokeslet est orienté transversalement, c’est-à-dire agissant perpendiculairement à l’axe de symétrie du montage. Le système est noyé dans un milieu fluide newtonien de viscosité dynamique $\eta$.

2.1. Équations directrices

Dans des conditions d’écoulement rampant, l’hydrodynamique est alors régie par les équations de Stokes (Happel & Brenner, 1983)

(1a) $-\mathrm{\nabla }p+\eta {\mathrm{\nabla }}^2\mathit{v}+\mathbf{F}\delta (\mathit{r}-{\mathit{r}}_0)=\mathbf{0},$(1a)

(1b) $\mathrm{\nabla }\cdot \mathit{v}=0,$(1b)

où $\mathit{v}$ et $p$ désignent respectivement les champs de vitesse et de pression du fluide. De plus, $\mathbf{F}$ est une force ponctuelle concentrée agissant sur le fluide environnant à la position $r_0=h{\hat{e}}_z$ tangente aux deux disques, où $h\in [-H/2,H/2]$. Le vecteur unitaire ${\hat{e}}_z$ est dirigé perpendiculairement aux plans contenant les disques. Nous choisissons l’origine de notre système de coordonnées comme le point central entre les deux disques. Sans perte de généralité, nous supposons que la force ponctuelle est orientée le long de la direction positive des $x$ telle que $\mathrm{F}=F{\hat{e}}_x$.

Avant d’aller plus loin, il convient de noter que le système étudié dans la présente contribution est complètement caractérisé par seulement deux paramètres sans dimension, $h/H$ et $R/H$. Par la suite, nous mettons à l’échelle toutes les longueurs par la distance de séparation $H$.

On identifie par l’indice 1 le domaine fluide sous le plan contenant le disque inférieur défini par $z\in [-\mathrm{\infty },-1/2]$, par l’indice 2 la région délimitée par les plans contenant les deux disques telle que $z\in [-1/2,1/2]$, et par l’indice 3 le domaine au dessus du plan contenant le disque supérieur, défini par $z\in [1/2,+\mathrm{\infty }]$.

La solution des équations de la dynamique des fluides (1) dans un milieu fluide non borné en l’absence des deux disques est exprimée en fonction de la fonction de Green en espace libre (Happel & Brenner, 1983). Les composantes de vitesse correspondantes $(v_r^{\mathrm{S}},v_{\varphi }^{\mathrm{S}},v_z^{\mathrm{S}})$ sont données dans le système de coordonnées cylindriques $(r,\varphi ,z)$ par

(2a) $v_r^{\mathrm{S}}=\frac{K}{\rho }\left(1+\frac{r^2}{{\rho }^2}\right)cos\varphi ,$(2a)

(2b) $v_{\varphi }^{\mathrm{S}}=-\frac{K}{\rho }sin\varphi ,$(2b)

(2c) $v_z^{\mathrm{S}}=\frac{Kr\left(z-h\right)}{{\rho }^3}cos\varphi ,$(2c)

où nous avons utilisé l’abréviation $K=F/\left(8\pi \eta \right)$. De plus, le champ de pression correspondant est exprimé sous la forme

(3) $p^{\mathrm{S}}=\frac{2Kr}{{\rho }^3}cos\varphi ,$(3)

où $\rho =|r-r_0|={\left(r^2+{(z-h)}^2\right)}^{1/2}$ représente la distance d’un point mesuré à partir de la position du Stokeslet.

La présence de disques de confinement peut être incorporée dans la solution du problème d’écoulement en considérant une solution complémentaire $(v^{\ast },p^{\ast })$ telle que sa superposition linéaire avec l’écoulement non borné

(4) $v=v^{\mathrm{S}}+v^{\ast },p=p^{\mathrm{S}}+p^{\ast },$(4)

satisfasse la régularité sous-jacente ainsi que les conditions aux limites. La solution complémentaire $(v^{\ast },p^{\ast })$ est aussi parfois appelée la solution image (Blake, 1971).

Étant donné que le Stokeslet agit perpendiculairement à l’axe central du système, le problème d’écoulement devient asymétrique par rapport à l’axe central. Dans ce cas, la solution de l’écoulement de Stokes peut commodément être exprimée par (Shail & Packham, 1987)

(5a) $v^{\ast }=\mathrm{\nabla }\mathrm{\Pi }+z\mathrm{\nabla }\mathrm{\Phi }-\mathrm{\Phi }{\hat{e}}_z+\mathrm{\nabla }\times \left(\mathrm{\Omega }{\hat{e}}_z\right),$(5a)

(5b) $p^{\ast }=2\eta \frac{\mathrm{\partial }\mathrm{\Phi }}{\mathrm{\partial }z}.$(5b)

Ici $\mathrm{\Pi }$, $\mathrm{\Psi }$ et $\mathrm{\Omega }$ sont trois fonctions harmoniques satisfaisant l’équation de Laplace, à savoir, ${\mathrm{\nabla }}^2\mathrm{\Pi }={\mathrm{\nabla }}^2\mathrm{\Psi }={\mathrm{\nabla }}^2\mathrm{\Omega }=0$. De plus

(6) $\mathrm{\Phi }=\mathrm{\Psi }+\frac{\mathrm{\partial }\mathrm{\Pi }}{\mathrm{\partial }z}.$(6)

La solution de l’équation de Laplace dans la géométrie actuelle peut être exprimée d’une manière générale en termes d’intégrales de Fourier-Bessel de la forme

(7a) ${\mathrm{\Pi }}_i=Kcos\varphi {\int }_0^{\mathrm{\infty }}\left(A_i^{+}{e}^{\lambda z}+A_i^{-}{e}^{-\lambda z}\right)J_1(\lambda r)\mathrm{d}\lambda ,$(7a)

(7b) ${\mathrm{\Psi }}_{\mathrm{i}}=Kcos\varphi {\int }_0^{\mathrm{\infty }}\left(B_i^{+}{e}^{\lambda z}+B_i^{-}{e}^{-\lambda z}\right)J_1(\lambda r)\mathrm{d}\lambda ,$(7b)

(7c) ${\mathrm{\Omega }}_{\mathrm{i}}=Ksin\varphi {\int }_0^{\mathrm{\infty }}\left(C_i^{+}{e}^{\lambda z}+C_i^{-}{e}^{-\lambda z}\right)J_1(\lambda r)\mathrm{d}\lambda ,$(7c)

où $i\in \{1,2,3\}$ identifie le domaine fluide considéré. Ici, $\lambda$ désigne le nombre d’onde (avec une dimension de longueur inverse), $J_1$ représente la fonction de Bessel de première espèce de premier ordre (Abramowitz & Stegun, 1965), et $(A_i^{\pm },B_i^{\pm },C_i^{\pm })$ sont des fonctions inconnues dépendantes du nombre d’onde qui doivent encore être déterminées à partir des conditions de régularité ainsi que des conditions aux limites décrites ci-dessous.

2.2. Régularité et conditions aux limites

Loin de la position de singularité, nous avons besoin de champs hydrodynamiques qui s’évanouissent à l’infini comme $\rho \to \mathrm{\infty }$. Cela nous conduit à $A_1^{-}=B_1^{-}=C_1^{-}=A_3^{+}=B_3^{+}=C_3^{+}=0$, réduisant considérablement le nombre de quantités inconnues. Ci-après, nous allégeons les notations en utilisant $A_1^{+}\equiv A_1$, $B_1^{+}\equiv B_1$, $C_1^{+}\equiv C_1$ dans le domaine 1, et $A_3^{-}\equiv A_3$, $B_3^{-}\equiv B_3$, $C_3^{-}\equiv C_3$ dans le domaine 3.

Comme conditions aux limites, nous exigeons la continuité des vitesses de fluide aux interfaces de domaine. Spécifiquement,

(8) ${\mathit{v}}_1-{\mathit{v}}_2{|}_{z=-\frac{1}{2}}={\mathit{v}}_2-{\mathit{v}}_3{|}_{z=\frac{1}{2}}=\mathbf{0}(r>0).$(8)

De plus, nous imposons, d’une part, des conditions aux limites de non-glissement et de non-pénétration (Lauga & Squires, 2005) au domaine interne $(r<R)$ défini par la surface du disque, ce qui donne

(9) ${\mathit{v}}_1{|}_{z=-\frac{1}{2}}={\mathit{v}}_2{|}_{z=\pm \frac{1}{2}}={\mathit{v}}_3{|}_{z=\frac{1}{2}}=\mathbf{0}(r<R).$(9)

D’autre part, nous demandons dans la région externe $(r>R)$ la continuité naturelle des contraintes normales aux interfaces entre les domaines fluides. Spécifiquement,

(10) ${\left.{\mathit{T}}_2-{\mathit{T}}_1\right|}_{z=-\frac{1}{2}}={\left.{\mathit{T}}_3-{\mathit{T}}_2\right|}_{z=\frac{1}{2}}=\mathbf{0}(r>R),$(10)

où ${\mathit{T}}_i:={\mathit{\sigma }}_i\cdot {\hat{e}}_z$ désigne le vecteur de contrainte hydrodynamique, ayant la forme suivante en coordonnées cylindriques

(11) $\begin{array}{cc}{T}_i& =\eta \left(\frac{\mathrm{\partial }{v_r}_i}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{v_z}_i}{\mathrm{\partial }r}\right){\hat{e}}_r+\eta \left(\frac{\mathrm{\partial }{v_{\varphi }}_i}{\mathrm{\partial }z}+\frac{1}{r}\frac{\mathrm{\partial }{v_z}_i}{\mathrm{\partial }\varphi }\right){\hat{e}}_{\varphi }\\ \hspace{0.17em}& +\left(-p_i+2\eta \frac{\mathrm{\partial }{v_z}_i}{\mathrm{\partial }z}\right){\hat{e}}_z,\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{r}i\in \{1,2,3\}.\end{array}$(11)

2.3. La formulation intégrale duale

En mécanique des fluides, l’approche aux équations intégrales duales a déjà été utilisée avec succès pour calculer l’écoulement visqueux axisymétrique dû au mouvement de deux disques coaxiaux de même taille (Kim & Chung, 1985), ou pour traiter l’écoulement induit par un Stokeslet près d’un disque antidérapant (Daddi-Moussa-Ider, Lisicki et al., 2020 ; Kim, 1983) ou une membrane élastique de taille finie (Daddi-Moussa-Ider, 2020 ; Daddi-Moussa-Ider et al., 2019), pour examiner l’écoulement visqueux entre deux disques rigides positionnés coaxialement (Daddi-Moussa-Ider, Sprenger et al., 2020, 2021), ainsi que pour décrire le mouvement auto-phorétique d’une sphère active automotrice à proximité d’un disque reposant sur une interface fluide-fluide plane (Daddi-Moussa-Ider, Vilfan et al., 2021). Suivant une approche similaire, les conditions aux limites de vitesse nulle à la surface des disques énoncées par Equation (9)(9) ${\mathit{v}}_1{|}_{z=-\frac{1}{2}}={\mathit{v}}_2{|}_{z=\pm \frac{1}{2}}={\mathit{v}}_3{|}_{z=\frac{1}{2}}=\mathbf{0}(r<R).$(9) dans la région interne $(r<R)$ peuvent être réarrangées pour donner les six équations intégrales suivantes,

(12a) ${\int }_0^{\mathrm{\infty }}{f}_1^{-}(\lambda )e^{-\frac{\lambda }{2}}{J}_0(r\lambda )\mathrm{d}\lambda ={\xi }_0^{+}(r)(r<R),$(12a)

(12b) ${\int }_0^{\mathrm{\infty }}{f}_3^{-}(\lambda )e^{-\frac{\lambda }{2}}{J}_0(r\lambda )\mathrm{d}\lambda ={\xi }_0^{-}(r)(r<R),$(12b)

(12c) ${\int }_0^{\mathrm{\infty }}{q}_1^{-}(\lambda )e^{-\frac{\lambda }{2}}{J}_1(r\lambda )\mathrm{d}\lambda ={\xi }_1^{+}(r)(r<R),$(12c)

(12d) ${\int }_0^{\mathrm{\infty }}{q}_3^{+}(\lambda )e^{-\frac{\lambda }{2}}{J}_1(r\lambda )\mathrm{d}\lambda ={\xi }_1^{-}(r)(r<R),$(12d)

(12e) ${\int }_0^{\mathrm{\infty }}{f}_1^{+}(\lambda )e^{-\frac{\lambda }{2}}{J}_2(r\lambda )\mathrm{d}\lambda ={\xi }_2^{+}(r)(r<R),$(12e)

(12f) ${\int }_0^{\mathrm{\infty }}{f}_3^{+}(\lambda )e^{-\frac{\lambda }{2}}{J}_2(r\lambda )\mathrm{d}\lambda ={\xi }_2^{-}(r)(r<R),$(12f)

où nous avons défini, par commodité, les abréviations

(13a) $f_1^{\pm }(\lambda )=\frac{1}{2}\lambda \left(\left(\lambda -2\right)A_1+B_1\pm 2C_1\right),$(13a)

(13b) $f_3^{\pm }(\lambda )=\frac{1}{2}\lambda \left(\left(\lambda -2\right)A_3-B_3\pm 2C_3\right),$(13b)

(13c) $q_i^{\pm }(\lambda )=\frac{1}{2}\left(\pm A_i{\lambda }^2-(\lambda +2)B_i\right)$(13c)

et utilisé la fameuse relation de récurrence des fonctions de Bessel de première espèce (Abramowitz & Stegun, 1965)

(14) $\frac{2k}{\lambda r}{J}_k(\lambda r)=J_{k-1}(\lambda r)+J_{k+1}(\lambda r).$(14)

Les fonctions radiales apparaissant à droite des équations (12) portent la signature du champ de vitesse dû au Stokeslet en espace libre et sont explicitement données par

(15a) ${\xi }_0^{\pm }(r)=\frac{3r^2+2(h\pm \frac{1}{2}{)}^2}{{\left(r^2+{(h\pm \frac{1}{2})}^2\right)}^{3/2}},$(15a)

(15b) ${\xi }_1^{\pm }(r)=\frac{(h\pm \frac{1}{2})r}{{\left(r^2+{(h\pm \frac{1}{2})}^2\right)}^{3/2}},$(15b)

(15c) ${\xi }_2^{\pm }(r)=\frac{-r^2}{{\left(r^2+{(h\pm \frac{1}{2})}^2\right)}^{3/2}}.$(15c)

Par la suite, les conditions aux limites liées à la continuité des contraintes tangentielles dans la région externe $(r>R)$ énoncées par Equation (10)(10) ${\left.{\mathit{T}}_2-{\mathit{T}}_1\right|}_{z=-\frac{1}{2}}={\left.{\mathit{T}}_3-{\mathit{T}}_2\right|}_{z=\frac{1}{2}}=\mathbf{0}(r>R),$(10) peuvent également être exprimées en termes d’équations intégrales comme

(16a) ${\int }_0^{\mathrm{\infty }}{g}_i(\lambda )J_1(\lambda r)\mathrm{d}\lambda =0(r>R),i\in \{1,4\},$(16a)

(16b) ${\int }_0^{\mathrm{\infty }}{g}_i(\lambda )J_0(\lambda r)\mathrm{d}\lambda =0(r>R),i\in \{2,5\},$(16b)

(16c) ${\int }_0^{\mathrm{\infty }}{g}_i(\lambda )J_2(\lambda r)\mathrm{d}\lambda =0(r>R),i\in \{3,6\},$(16c)

où $g_i$ forment le vecteur $g=(g_1,g_2,g_3,g_4,g_5,g_6{)}^{\mathrm{T}}$ et sont des quantités inconnues dépendantes du nombre d’onde, données par

(17) $g={\mathrm{\Lambda }}_{13}\cdot {\mathcal{Z}}_{13}+{\mathrm{\Lambda }}_2\cdot {\mathcal{Z}}_2.$(17)

Ici,

(18) ${\mathrm{\Lambda }}_{13}=\left(\begin{array}{cc}{\mathrm{\Lambda }}^{+}& \mathbf{0}\\ \mathbf{0}& {\mathrm{\Lambda }}^{-}\end{array}\right),$(18)

où nous avons défini les sous-matrices

(19) ${\mathrm{\Lambda }}^{\pm }=\left(\begin{array}{ccc}-\lambda {\sigma }^{-}& \mp {\phi }_{+}^{-}& 0\\ \pm \lambda {\phi }_{-}^{-}& {\sigma }^{-}& \mp {\sigma }^{-}\\ \pm \lambda {\phi }_{-}^{-}& {\sigma }^{-}& \pm {\sigma }^{-}\end{array}\right),$(19)

avec ${\phi }_{+}^{\pm }=\lambda \left(\lambda +2\right)e^{\pm \frac{\lambda }{2}}$, ${\phi }_{-}^{\pm }=\lambda \left(\lambda -2\right)e^{\pm \frac{\lambda }{2}}$, et ${\sigma }^{\pm }={\lambda }^2{e}^{\pm \frac{\lambda }{2}}$. En plus

(20) ${\mathrm{\Lambda }}_2=\left(\begin{array}{cc}{\mathrm{\Lambda }}_1^{+}& {\mathrm{\Lambda }}_2^{+}\\ {\mathrm{\Lambda }}_1^{-}& {\mathrm{\Lambda }}_2^{-}\end{array}\right),$(20)

où nous avons défini

(21) ${\mathrm{\Lambda }}_1^{\pm }=\left(\begin{array}{ccc}\pm \lambda {\sigma }^{\mp }& \mp \lambda {\sigma }^{\pm }& \pm {\phi }_{\pm }^{\mp }\\ \mp \lambda {\phi }_{\mp }^{\mp }& \mp \lambda {\phi }_{\pm }^{\pm }& \mp {\sigma }^{\mp }\\ \mp \lambda {\phi }_{\mp }^{\mp }& \mp \lambda {\phi }_{\pm }^{\pm }& \mp {\sigma }^{\mp }\end{array}\right)$(21)

et

(22) ${\mathrm{\Lambda }}_2^{\pm }=\left(\begin{array}{ccc}\pm {\phi }_{\mp }^{\pm }& 0& 0\\ \pm {\sigma }^{\pm }& {\sigma }^{\mp }& -{\sigma }^{\pm }\\ \pm {\sigma }^{\pm }& -{\sigma }^{\mp }& {\sigma }^{\pm }\end{array}\right).$(22)

Ici, ${\mathcal{Z}}_2={\left(A_2^{-},B_2^{-},C_2^{-},A_2^{+},B_2^{+},C_2^{+}\right)}^{\mathrm{T}}$ sont les constantes dépendantes du nombre d’onde du domaine 2 et ${\mathcal{Z}}_{13}={\left(A_1,B_1,C_1,A_3,B_3,C_3\right)}^{\mathrm{T}}$ sont les constantes dépendantes du nombre d’onde des domaines 1 et 3.

Enfin, en utilisant les conditions aux limites de continuité de vitesse énoncées par Equation (8)(8) ${\mathit{v}}_1-{\mathit{v}}_2{|}_{z=-\frac{1}{2}}={\mathit{v}}_2-{\mathit{v}}_3{|}_{z=\frac{1}{2}}=\mathbf{0}(r>0).$(8) , les fonctions dépendantes du nombre d’onde associées au domaine 2 (abrégé par ${\mathcal{Z}}_2$) peuvent facilement être exprimées en termes de ceux associés aux domaines 1 et 3 (abrégés par ${\mathcal{Z}}_{13}$). En raison de leur complexité et de leur longueur, les expressions correspondantes ont été omises ici.

Suivant les recettes bien établies par Sneddon (1960) et Copson (1961), nous introduisons de nouvelles fonctions inconnues ${\mathcal{G}}_i:[0,R]\to \mathbb{R}$, pour $i=1,\dots ,6$, et cherchons la solution des équations intégrales énoncées par Equation (16) sous la forme intégrale suivante

(23a) $g_i(\lambda )=2{\lambda }^{\frac{1}{2}}{\int }_0^R{\mathcal{G}}_i(t)J_{\frac{3}{2}}(\lambda t)\mathrm{d}t,i\in \{1,4\},$(23a)

(23b) $g_i(\lambda )=2{\lambda }^{\frac{1}{2}}{\int }_0^R{\mathcal{G}}_i(t)J_{\frac{1}{2}}(\lambda t)\mathrm{d}t,i\in \{2,5\},$(23b)

(23c) $g_i(\lambda )=2{\lambda }^{\frac{1}{2}}{\int }_0^R{\mathcal{G}}_i(t)J_{\frac{5}{2}}(\lambda t)\mathrm{d}t,i\in \{3,6\}.$(23c)

Le principal avantage de l’adoption de cette forme de solution est que les conditions aux limites de la région externe (16) sont automatiquement satisfaites en utilisant l’identité suivante (Abramowitz & Stegun, 1965),

(24) ${\int }_0^{\mathrm{\infty }}{\lambda }^{\frac{1}{2}}{J}_k(\lambda r)J_{k+\frac{1}{2}}(\lambda t)\mathrm{d}\lambda =0(0<t<r),$(24)

où $k$ est un entier positif arbitraire.

Ensuite, en changeant l’ordre d’intégration par rapport aux variables $t$ et $\lambda$, le problème interne (12) se réduit à un ensemble de six équations intégrales de la forme

(25) $\sum _{j=1}^6{\int }_0^R{K}_{ij}(r,t){\mathcal{G}}_j(t)\mathrm{d}t={\mathrm{\Xi }}_i(r),i=1,\dots ,6,$(25)

où $\mathbf{\Xi }:=\left({\xi }_0^{+},{\xi }_0^{-},{\xi }_1^{+},{\xi }_1^{-},{\xi }_2^{+},{\xi }_2^{-}\right)$ sont les fonctions données précédemment par Equation (15). Les fonctions noyau $K_{ij}$, avec $i,j=1,\dots ,6$, comportent des intégrales impropres (infinies) par rapport au nombre d’onde $\lambda$ (voir Appendix A pour leurs expressions), qui peuvent être évaluées à la fois numériquement (Tanzosh & Stone, 1996) et analytiquement. Dans le présent travail, nous avons adopté cette dernière voie et obtenu des expressions explicites de ces intégrales. En outre, Equation (25)(25) $\sum _{j=1}^6{\int }_0^R{K}_{ij}(r,t){\mathcal{G}}_j(t)\mathrm{d}t={\mathrm{\Xi }}_i(r),i=1,\dots ,6,$(25) forment un système couplé d’équations intégrales de Fredholm de première espèce pour les six fonctions inconnues ${\mathcal{G}}_i(t)$.

2.3.1. Résolution numérique d’équations intégrales

Les fonctions noyaux compliquées apparaissant dans Equation (25)(25) $\sum _{j=1}^6{\int }_0^R{K}_{ij}(r,t){\mathcal{G}}_j(t)\mathrm{d}t={\mathrm{\Xi }}_i(r),i=1,\dots ,6,$(25) nous empêchent d’obtenir des solutions analytiques pour les fonctions ${\mathcal{G}}_i(t)$. Par conséquent, nous adoptons une procédure numérique. Nous employons la quadrature Legendre-Gauss (Golub & Welsch, 1969) et évaluons les intégrales aux $N$ nœuds gaussiens dans l’intervalle $[0,R]$. Cela réduit le système d’équations intégrales à un système linéaire de $6N$ équations, qui peut être facilement résolu en utilisant des méthodes numériques standards (Ostrowski, 2016). Avec les valeurs discrètes connues de ${\mathcal{G}}_i(t_j)$, où $i=1,\dots ,6$ et $j=1,\dots ,N$, nous utilisons à nouveau une technique de quadrature similaire pour évaluer les intégrations dans Equation (23) par rapport à la variable $t$.

Pour aborder les intégrales impropres par rapport à la variable $\lambda$ sur l’intervalle $[0,+\mathrm{\infty }]$ dans Equation (7), nous employons une transformation de variable de la forme $\lambda =tanu$. Cela fournit des intégrandes dans la limite d’intégration modifiée, $u\in [0,\pi /2]$. Ensuite, nous utilisons à nouveau la règle de quadrature de Legendre-Gauss pour évaluer les valeurs discrètes de $g_i(u_m)$ à $M$ nœuds gaussiens, où $m\in [1,M]$.

Après avoir obtenu les variables $g_i(u_m)$, nous procédons à la récupération des quantités dépendantes du nombre d’onde ${\mathcal{Z}}_{13}$ et ${\mathcal{Z}}_2$ en utilisant Equation (17)(17) $g={\mathrm{\Lambda }}_{13}\cdot {\mathcal{Z}}_{13}+{\mathrm{\Lambda }}_2\cdot {\mathcal{Z}}_2.$(17) et obtenons les champs de vitesse en effectuant des intégrations par rapport au nombre d’onde $\lambda$, comme indiqué par Equation (7). Bien que la méthodologie actuelle puisse sembler compliquée à première vue, la méthode atténue la nécessité de résoudre une équation différentielle en utilisant une technique de discrétisation directe dans un domaine tridimensionnel et fournit une formulation alternative ne nécessitant qu’une quadrature numérique unidimensionnelle. Un test détaillé d’indépendance de la grille lié au choix des points de quadrature a été fourni en Appendix B. Nous montrons dans Figure B1 l'erreur de quadrature dans l'évaluation de la vitesse d'écoulement par rapport au nombre de nœuds.

2.3.2. Comparaison avec des simulations numériques par la méthode des éléments finis

Pour la validation, nous comparons les solutions avec des simulations numériques par éléments finis. Pour discrétiser les équations de Stokes, des éléments finis quadratiques sont utilisés sur une grille hexaédrique irrégulière. Comme l’approche quadratique d’ordre égal n’est pas stable inf-sup, une stabilisation de la projection locale est ajoutée (Becker & Braack, 2001). Le domaine de calcul est artificiellement restreint à un hexaèdre avec des côtés $10R\times 10R\times 10$. Sur la limite extérieure, la condition de contrainte nulle $\left(\eta (\mathrm{\nabla }v+\mathrm{\nabla }{v}^T)-pI\right)\cdot n=0$ est définie. L’écoulement est entraîné par la force ponctuelle qui s’intègre exactement dans la formulation faible comme un Dirac du côté droit. Des éléments finis isoparamétriques quadratiques (Richter, 2017 ; Section 4.2.3) sont utilisés pour approximer la géométrie des deux disques.

Afin de résoudre la singularité, le maillage de calcul est affiné de manière adaptative avec la résolution la plus élevée le long des deux disques et en particulier à la position de la singularité. La discrétisation la plus fine utilisée pour produire les résultats implique environ 15 millions de degrés de liberté. Les systèmes d’équations linéaires résultants sont inversés avec un solveur multigrille parallèle (Failer & Richter, 2020). Tous les calculs sont effectués dans la bibliothèque logicielle d’éléments finis Gascoigne 3d (Becker et al., 2020).

2.4. Limite de plaque infinie, tel que $R\to \mathrm{\infty }$

Dans la limite des disques infiniment étendus, le problème interne énoncé par Equation (12) devient valable dans tout le domaine semi-infini $r\in [0,+\mathrm{\infty }]$. Ensuite, les fonctions inconnues $g_i(\lambda )$ peuvent être déterminées en transformant les fonctions auxiliaires définies dans Equation (15). Ceci est obtenu en appliquant la transformée de Hankel (Piessens, 2000) de la forme

(26) ${\hat{\xi }}_k^{\pm }(\lambda )={\int }_0^{\mathrm{\infty }}r{\xi }_k^{\pm }(r)J_k(\lambda r)\mathrm{d}rk\in \{0,1,2\}.$(26)

Une utilisation ultérieure de la propriété d’orthogonalité des fonctions de Bessel (Abramowitz & Stegun, 1965)

(27) ${\int }_0^{\mathrm{\infty }}r{J}_k(\lambda r)J_k(\lambda { }^{\mathrm{\prime }}r)\mathrm{d}r={\lambda }^{-1}\delta \left(\lambda -\lambda { }^{\mathrm{\prime }}\right)$(27)

nous laisse avec un système d’équations linéaires à résoudre pour $g={\left(g_1,g_2,g_3,g_4,g_5,g_6\right)}^{\mathrm{T}}$. Spécifiquement,

(28) $\mathbf{\Lambda }\cdot \mathbf{g}=\stackrel{\mathbf{ˆ}}{\xi },$(28)

où

(29) $\mathbf{\Lambda }=\left(\begin{array}{cccccc}0& 3{\delta }_1& -{\delta }_1& 2{\delta }_2& {\delta }_4& {\delta }_3\\ 2{\delta }_2& -{\delta }_4& -{\delta }_3& 0& -3{\delta }_1& {\delta }_1\\ 2{\delta }_1& 0& 0& -2{\delta }_3& -{\delta }_2& -{\delta }_2\\ 2{\delta }_3& -{\delta }_2& -{\delta }_2& -2{\delta }_1& 0& 0\\ 0& -{\delta }_1& 3{\delta }_1& 2{\delta }_2& {\delta }_3& {\delta }_4\\ 2{\delta }_2& -{\delta }_3& -{\delta }_4& 0& {\delta }_1& -3{\delta }_1\end{array}\right),$(29)

où nous avons défini ${\delta }_1=1/\left(8{\lambda }^2\right)$, ${\delta }_2=e^{-\lambda }/\left(8\lambda \right)$, ${\delta }_3=\left(\lambda +1\right)e^{-\lambda }/\left(8{\lambda }^2\right)$, et ${\delta }_4=\left(\lambda -3\right)e^{-\lambda }/\left(8{\lambda }^2\right)$. De plus, $\hat{\xi }={\left({\tau }_1^{+},{\tau }_1^{-},{\tau }_2^{+},{\tau }_2^{-},{\tau }_3^{+},{\tau }_3^{-}\right)}^{\mathrm{T}}$ où ${\tau }_1^{\pm }=\left(3/\lambda \mp h-1/2\right)e^{-\lambda \left(1/2\pm h\right)}$, ${\tau }_2^{\pm }=\pm \left(1/2\pm h\right)e^{-\lambda \left(1/2\pm h\right)}$, et ${\tau }_3^{\pm }=-\left(1/\lambda \pm h+1/2\right)e^{-\lambda \left(1/2\pm h\right)}$.

Le système linéaire énoncé par Equation (28)(28) $\mathbf{\Lambda }\cdot \mathbf{g}=\stackrel{\mathbf{ˆ}}{\xi },$(28) peut être facilement résolu analytiquement par inversion matricielle, donnant des expressions compactes pour les fonctions inconnues $g$. Les expressions pour ${\mathcal{Z}}_2$ et ${\mathcal{Z}}_{13}$ peuvent ensuite être obtenues en utilisant Equation (17).

3. Résultats et discussions

3.1. Hydrodynamic mobility

Dans l’étude de la mécanique des suspensions (Batchelor, 2000 ; Guazzelli & Morris, 2011), la fonction de mobilité hydrodynamique sert à relier la vitesse des particules à la force qu’elles subissent. Dans le cas d’une particule sphérique se translatant dans un fluide newtonien non borné, la loi de Stokes connue énonce la mobilité des particules comme ${\mu }_0=(6\pi \eta a{)}^{-1}$, où $a$ est le rayon de la particule. Pour étudier l’influence des disques sur la force de traînée subie par une particule ponctuelle qui est forcée de se déplacer parallèlement aux surfaces du disque et qui, au moment de l’observation, se trouve juste sur l’axe central de la configuration, nous analysons la correction d’ordre dominant à la mobilité hydrodynamique par rapport à la situation en l’absence des disques. Cette quantité peut être obtenue en évaluant le champ de la solution image à la position de la particule. Spécifiquement,

(30) $\mathrm{\Delta }\mu =F^{-1}\underset{(r,z)\to (0,h)}{lim}{v}_x^{\ast }.$(30)

En rééchelonnant par la mobilité en bulk ${\mu }_0$, nous définissons le facteur de correction d’ordre principal mis à l’échelle à la mobilité de Stokes tel que

(31) $k=-\frac{1}{a}\frac{\mathrm{\Delta }\mu }{{\mu }_0}.$(31)

En utilisant la solution exacte, le facteur de correction peut être écrit sous la forme intégrale

(32) $\begin{array}{cc}k& =\frac{3}{8}{\int }_0^{\mathrm{\infty }}\lambda (\left(\left(A_2^{-}\lambda -B_2^{-}\right)h-A_2^{-}-C_2^{-}\right)e^{-\lambda h}\\ \hspace{0.17em}& -e^{\lambda h}\left(\left(A_2^{+}\lambda +B_2^{+}\right)h+A_2^{+}+C_2^{+}\right))\mathrm{d}\lambda .\end{array}$(32)

La Figure 2 représente la variation du facteur de correction de mobilité d’ordre dominant en fonction du rayon des disques positionnés coaxialement pour différents emplacements verticaux de la singularité. Dans la limite extrême où le rayon du disque est suffisamment large pour présenter les caractéristiques des deux plaques planes infiniment étendues, le facteur $k$ atteint une valeur asymptotique. L’amplitude décroissante du facteur de correction de mobilité $k$ avec le rayon décroissant des disques indique une résistance réduite au mouvement des particules. Dans la limite $R\to \mathrm{\infty }$, le facteur de correction est en plein accord avec la solution rapportée par Swan and Brady (2010) qui ont utilisé une technique de transformée de Fourier bidimensionnelle.

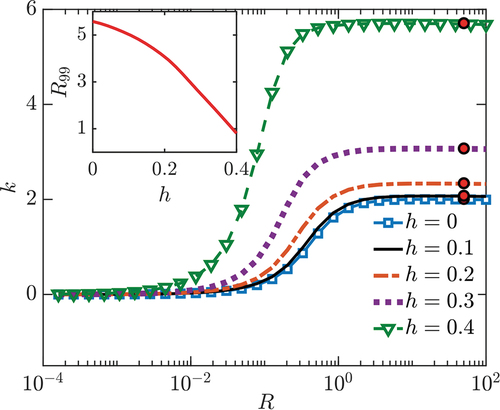
Figure 2. Facteur de correction de mobilité $k$ en fonction du rayon des disques $R$ pour une particule ponctuelle forcée située à différentes distances verticales $h$ du centre entre les deux disques disposés coaxialement. Les marqueurs rouges représentent les résultats obtenus par Swan and Brady (2010). L’encart montre les variations du rayon $R_{99}$, une mesure de la taille du disque à partir de laquelle la mobilité devient presque identique à celle entre les disques infiniment étendus, avec la distance $h$.

Pour quantifier le rayon de coupure en dessous duquel la taille finie du disque devient importante, nous calculons le rayon du disque, $R_{99}$, pour lequel 99% de la correction de mobilité entre des disques infiniment étendus est atteint. L’encart de Figure 2 montre que le rayon $R_{99}$ est maximum à $h=0$ avec une valeur de $R_{99}\simeq 5,58$. Cette valeur peut facilement être comparée à la valeur correspondante d’environ 0,62 rapportée précédemment pour un Stokeslet agissant normalement aux disques (Daddi-Moussa-Ider, Sprenger et al., 2020). Cela suggère une nature intrinsèquement distincte de l’effet de disque fini sur le mouvement de particules ponctuelles orientées différemment. De plus, la diminution progressive de $R_{99}$ avec la distance $h$ signifie le fait que la finitude du disque devient de plus en plus cruciale à mesure que le Stokeslet est éloigné de la surface du disque le plus proche.

3.1.1. Comparaison avec l’approximation d’Oseen

En présence de deux obstacles suffisamment séparés, le facteur de correction peut être adéquatement approché en superposant les contributions individuelles résultant de chaque obstacle (Benesch et al., 2003; Daddi-Moussa-Ider et al., 2016b ; Daddi-Moussa-Ider, Lisicki, Mathijssen et al., 2018 ; Daddi-Moussa-Ider, Löwen et al., 2021 ; Dufresne et al., 2001; Mathijssen et al., 2016 ; Polin et al., 2006). Dans ce qui suit, nous examinons la précision et la pertinence de l’approximation de superposition linéaire suggérée originellement par Oseen (1928). Dans cette approche, la mobilité hydrodynamique entre deux parois parallèles pourrait être déterminée de manière appropriée en superposant les contributions individuelles provenant de chaque paroi indépendamment. Par conséquent, les conditions aux limites mixtes ne sont plus satisfaites au niveau des plans contenant les deux disques. Pour évaluer le succès de cette approximation pour la finitude des disques de confinement, nous utilisons la solution monodisque rapportée précédemment par Miyazaki (1984). En utilisant notre notation, le facteur de correction de mobilité à proximité d’un seul disque peut être écrit sous la forme suivante (Daddi-Moussa-Ider, 2020)

(33) $\frac{\mathrm{\Delta }\mu }{{\mu }_0}=-\frac{3}{4\pi }\left(\frac{3+5{\xi }^2}{{\left(1+{\xi }^2\right)}^2}+\frac{3}{\xi }arctan\left(\frac{1}{\xi }\right)\right)\frac{a}{R},$(33)

où $\xi =b/R$ avec $b$ désignant la distance entre la particule et le centre du disque considéré.

Suivant l’approche d’Oseen, le facteur de correction d’ordre dominant de la mobilité hydrodynamique peut être approximé simplement en ajoutant les corrections d’ordre dominant résultant des disques individuels. Puis,

(34) $k_{\mathrm{S}\mathrm{u}\mathrm{p}}=-\frac{1}{a}\left({\left.\frac{\mathrm{\Delta }\mu }{{\mu }_0}\right|}_{b=\frac{1}{2}-h}+{\left.\frac{\mathrm{\Delta }\mu }{{\mu }_0}\right|}_{b=\frac{1}{2}+h}\right).$(34)

Pour tester la pertinence de l’approximation d’Oseen, nous calculons l’erreur $\mathcal{E}$ par rapport à la solution exacte présentée dans la Section 3.1. Dans Figure 3 nous traçons l’erreur maximale ${\mathcal{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ obtenue dans l’approximation de superposition pour une distance verticale $h$ séparant la particule ponctuelle de l’origine. Nous décrivons également le rayon des disques correspondant à cette erreur maximale $R_{\mathrm{m}\mathrm{a}\mathrm{x}}$. La figure montre que les résultats approximatifs sont en quelque sorte erronés quand la particule se localise vers le plan médian entre les disques, ce qui implique jusqu’à environ 20% d’erreur pour $h=0$. Cette erreur maximale se trouve atteinte pour le rayon des disques $R\simeq 1$. L’erreur la plus élevée est particulièrement importante compte tenu du fait que la taille finie des disques a un impact significatif sur la mobilité dans cette situation particulière, comme quantifié dans Figure 2. On peut également déduire de Figure 3 que, comme la particule est située plus près de l’un des disques, l’erreur maximale diminue de manière monotone et finit par disparaître complètement comme $h\to 1/2$. Le rayon des disques $R_{\mathrm{m}\mathrm{a}\mathrm{x}}$ correspondant à l’erreur maximale augmente de façon monotone avec $h$ et diverge à l’infini pour $h\to 1/2$.

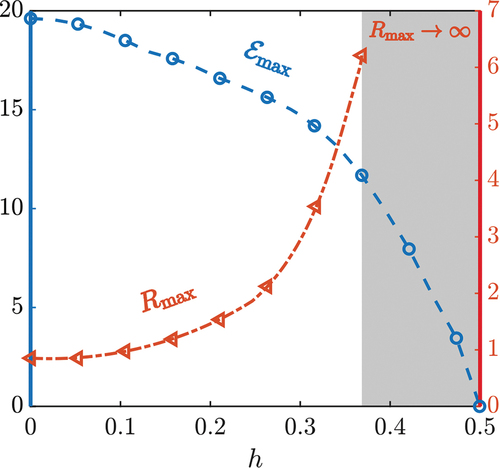
Figure 3. L’axe de gauche est associé à l’erreur relative maximale dans le facteur de correction de mobilité en utilisant la superposition d’Oseen par rapport à notre solution exacte. De plus, l’axe de droite identifie le rayon du disque pour lequel chaque valeur de ${\mathcal{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ a été obtenue. Dans la région marquée en gris, $R_{\mathrm{m}\mathrm{a}\mathrm{x}}$ continue de diverger vers l’infini.

Par conséquent, on peut conclure que l’approximation par superposition peut généralement bien fonctionner, sauf dans la région proche du plan médian entre les deux disques où l’approximation ne parvient pas à capturer la tendance correcte de variation du facteur de correction de mobilité.

3.2. Description du champ d’écoulement

Pour examiner la nature tridimensionnelle du champ d’écoulement asymétrique, nous montrons dans Figure 4 un quiver tracé du champ d’écoulement induit par des Stokeslets positionnés à (a) $h=0$ et (b) $h=0.25$ agissant entre deux disques parallèles (affichés en gris.) Les lignes de courant sont présentées dans les trois plans normaux donnés par $x=2$, $y=1$ et $z=-1$. Contrairement au champ d’écoulement axisymétrique simpliste précédemment étudié (Daddi-Moussa-Ider, Sprenger et al., 2020), la configuration asymétrique considérée dans la présente étude révèle un comportement d’écoulement fondamentalement différent. En particulier, la présence des deux disques de confinement conduit à une forte altération des lignes de courant notamment dans le plan $z=-1$ parallèle aux surfaces des disques. Les perturbations d’écoulement créées par la singularité de force ponctuelle pointant dans une direction entre les deux disques dépendent fortement de l’emplacement vertical $h$ de la singularité.

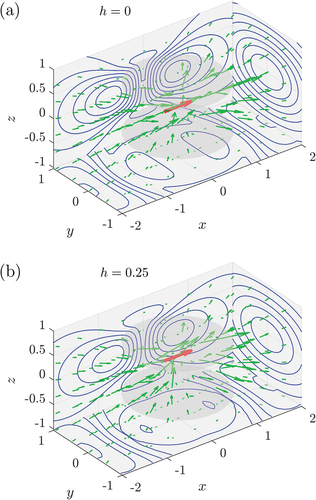
Figure 4. Tracé tridimensionnel du champ d’écoulement induit par une singularité de force ponctuelle (indiquée par une flèche rouge) agissant tangente à deux disques antidérapants positionnés coaxialement (en gris.) Les résultats sont présentés pour deux valeurs différentes de l’emplacement de la singularité pour (a) $h=0$ et (b) $h=0.25$. Les lignes d’écoulement sont représentées sur trois coupes planes perpendiculaires pour mettre en évidence la nature asymétrique de l’écoulement.

Dans Figure 5, les lignes de vitesse ainsi que la magnitude de la vitesse ont été évaluées pour trois valeurs de $h$ tandis que le rayon des disques est fixé à $R=1$. Les résultats correspondants des simulations numériques par éléments finis dans les panneaux de droite montrent un très bon accord avec notre théorie semi-analytique. Pour $h=0$, le champ de vitesse est symétrique par rapport au plan médian, comme prévu. On peut également observer l’existence de petits tourbillons situés à proximité des deux disques. Néanmoins, à mesure que le Stokeslet s’approche de l’un des disques, ce motif symétrique est considérablement déformé. En raison de la continuité de l’écoulement, un renforcement correspondant au motif d’écoulement circulatoire est observée à côté du disque plus loin du Stokeslet.

Figure 5. Champ d’écoulement induit par un Stokeslet situé à différents emplacements verticaux $h$. Les panneaux de haut en bas représentent respectivement les cas avec $h=0,0,25\mathrm{e}\mathrm{t}0,375$. Les panneaux de gauche (a, c, e) représentent les résultats de la présente théorie semi-analytique, tandis que les résultats des simulations numériques correspondantes sont présentés à des fins de comparaison dans les panneaux de droite (b, d, f). Dans tous les cas, $R=1$ a été choisi.

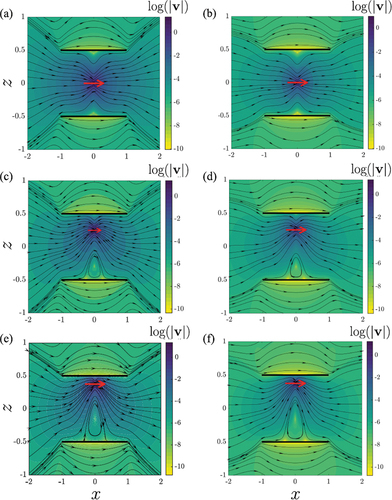
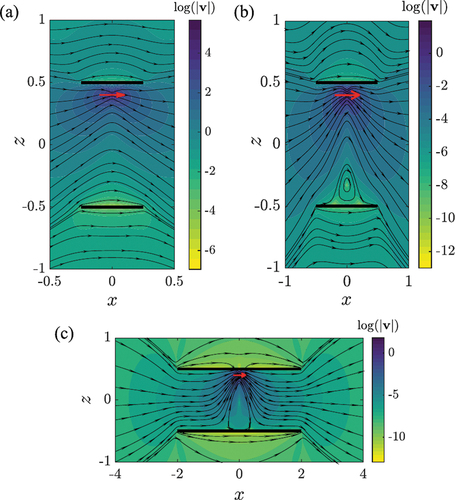
Alors que l’emplacement variable du Stokeslet donne essentiellement une évaluation de l’entrave à l’écoulement par la paroi, le rayon variable du disque indique les contributions relatives des surfaces solides et des zones sans obstacle situées dans les plans $z=\pm 1/2$. Ainsi, pour modifier les motifs d’écoulement, nous avons montré le champ de vitesse pour un rayon de disque variable, mais pour un emplacement fixe du Stokeslet en Figure 6. Apparemment, le plus gros vortex près du disque le plus éloigné devient plus fort avec l’augmentation du rayon du disque, et une suppression correspondante de l’autre vortex se produit.

Figure 6. Tourbillons de plus en plus prononcés avec un rayon de disque croissant. Les panels (a–c) correspondent respectivement aux cas de $R=0,25,0,5\mathrm{e}\mathrm{t}2$. Dans tous les cas, nous choisissons $h=0,4$.

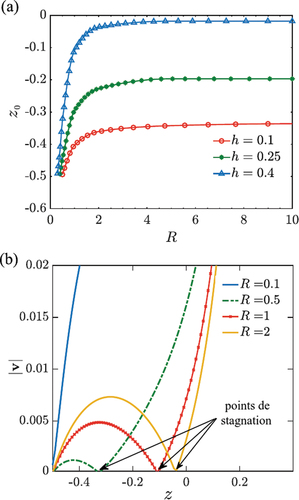
Une évaluation systématique de l’existence et de la localisation du vortex est effectuée en analysant la localisation verticale $z_0$ des points de stagnation qui apparaissent dans le champ d’écoulement à $x=0$. Selon Figure 7(a), un tel point de stagnation apparaîtrait lorsque le rayon du disque dépasse une valeur minimale. Cette limite inférieure a été trouvée comme $R=0,4\mathrm{e}\mathrm{t}0,3$ pour $h=0,1\mathrm{e}\mathrm{t}0,4$, respectivement. Avec une augmentation supplémentaire du rayon du disque, la contribution non-glissement dans le champ d’écoulement sur les surfaces des disques commence à dominer l’influence de la zone de continuité des contraintes dans les plans du disque à $z=\pm 1/2$ pour $r>R$. Le point de stagnation s’éloigne du disque voisin avec un rayon $R$ croissant des disques, comme le montre Figure 7(b). Enfin, dans la limite de $R\to \mathrm{\infty }$, l’emplacement des points de stagnation analysés ne change plus et sature à une valeur constante pour cet emplacement vertical particulier $h$ du Stokeslet.

Figure 7. (a) Variation de la position verticale du point de stagnation $z_0$ avec l’augmentation du rayon du disque $R$ pour différents emplacements verticaux $h$ du Stokeslet inducteur d’écoulement. Le panneau (b) met en évidence l’emplacement des points de stagnation lorsque nous traversons verticalement du disque inférieur à l’emplacement $(x,z)=\left(0,0,4\right)$ du Stokeslet.

4. Conclusions

Pour résumer, nous avons présenté une théorie semi-analytique qui décrit le champ d’écoulement induit par une singularité ponctuelle de force agissant parallèlement aux surfaces de deux disques rigides infiniment minces positionnés coaxialement. La singularité est située le long de l’axe des disques. Des conditions de non-glissement prévalent sur les surfaces des disques. Nous avons formulé le problème dans le régime à faible nombre de Reynolds comme un problème aux limites mixtes que nous avons ensuite réduit en un système d’équations intégrales duales. Cela a réduit la méthodologie de résolution des fonctions de Green à une quadrature numérique unidimensionnelle et a ainsi réduit la nécessité de résoudre les équations hydrodynamiques en utilisant des techniques de discrétisation directe dans l’ensemble du domaine spatial tridimensionnel. Ensuite, nous avons fourni une formulation intégrale de la correction d’ordre dominant de la fonction de mobilité hydrodynamique pour une particule ponctuelle et évalué la précision et la pertinence de l’approximation de superposition simpliste qui traite l’influence des deux disques séparément l’un de l’autre. Nous avons constaté que cette approximation fonctionne raisonnablement bien à proximité des disques, mais peut conduire à une erreur allant jusqu’à 20 % dans le cas contraire. Les résultats montrent qu’une distance de décalage vertical du Stokeslet par rapport au centre géométrique du système conduit à une force de rupture de symétrie dans la distribution de l’écoulement du fluide. D’autre part, la finitude des disques joue un rôle clé dans la dictée du modèle de vorticité asymétrique dans la région entre les disques. Au fur et à mesure que le rayon du disque augmente, un décalage correspondant du point de stagnation vers l’emplacement de la singularité a été observé.

Ces résultats pourraient être pertinents dans un certain nombre d’applications biologiques et technologiques. En génomique, par exemple, les mobilités dérivées ici pourraient fournir des informations sur la translocation de petites particules à travers les nanopores, ce qui est important pour le séquençage des nanopores (Deamer et al., 2016). De même, en nanotechnologie, nos travaux pourraient être pertinents pour le mouvement des points quantiques (QD) dans les nanoconstrictions de graphène (Todd et al., 2009). À leur tour, les points quantiques peuvent être utilisés pour démêler la dynamique de diffusion des récepteurs de la glycine en biologie cellulaire (Dahan et al., 2003).

Les solutions dérivées ici pourraient être liées fermement à l’hydrodynamique des micro-nageurs et particules actives automotrices (Bechinger et al., 2016; Cates & Tailleur, 2015; Elgeti et al., 2015 ; Gompper et al., 2020 ; Illien et al., 2017 ; Lauga, 2016, 2020 ; Lauga & Powers, 2009 ; Menzel, 2015 ; Shaebani et al., 2020 ; Zöttl & Stark, 2016). Plus précisément, l’écoulement de Stokeslet peut être utilisé pour construire une expansion multipolaire, ce qui permet de prédire les interactions hydrodynamiques de micro-organismes ou de micro-robots avec leurs environnements confinés (Daddi-Moussa-Ider, Lisicki et al., 2018 ; Daddi-Moussa-Ider, Lisicki, Mathijssen et al., 2020 ; Mathijssen et al., 2016 ; Poddar et al., 2021, 2020 ; Sprenger et al., 2020). Un autre aspect intéressant qui pourrait être exploré est de savoir comment les disques de taille finie pourraient entraîner un effet de blindage, où les écoulements sont amortis par le confinement partiel. On pourrait envisager que des organismes puissent se cacher entre des parois, de sorte que les écoulements qu’ils génèrent ne soient pas détectés par des prédateurs mécano-sensibles (Mathijssen et al., 2019). On pourrait alors se demander quelle doit être la taille des disques pour réduire d’un certain facteur les écoulements multipolaires en un point extérieur à la cage.

Plus généralement, les fonctions de Green présentées pourraient être appliquées à l’hydrodynamique des systèmes de matière vivante et active (Marchetti et al., 2013 ; Needleman & Dogic, 2017). Alors que l’injection d’énergie locale conduit souvent à des instabilités hydrodynamiques et à des turbulences dites actives, le confinement peut aider à stabiliser cette dynamique (Wioland et al., 2013) et conduire à une auto-organisation (Doostmohammadi et al., 2018 ; Lushi et al., 2014). Le contrôle de systèmes actifs avec des confinements partiels, illustrés par des disques de taille finie, pourrait être d’un intérêt considérable.

Dans la présente contribution, nous avons supposé pour simplifier que la force ponctuelle est située sur l’axe central des deux disques rigides positionnés coaxialement. Il serait très intéressant d’ailleurs d’étudier la situation générale du positionnement arbitraire. Différentes voies d’approche du problème peuvent consister à utiliser des fonctions de Green et de Neumann complétées par la technique des fonctions de bord (Miyazaki, 1984). Des composantes supplémentaires du tenseur de mobilité, y compris les couplages hydrodynamiques et les mobilités en rotation, devraient être élaborés. Ces aspects seraient d’un grand intérêt pour être examinés dans une future enquête.

Déclaration de divulgation

L’auteur ne déclare aucun intérêt concurrent.

Remerciements

L’auteur tient à remercier profondément A. Poddar pour sa collaboration précoce et son soutien technique, pour diverses discussions stimulantes, ainsi que pour son assistance et son aide dans la préparation des figures de ce manuscrit. En outre, je tiens à remercier sincèrement S. Chakraborty et A. Bandopadhyay pour une discussion précieuse, T. Richter pour avoir généreusement partagé les données de simulations par éléments finis, A. M. Menzel et H. Löwen pour des suggestions perspicaces. Je voudrais également remercier le soutien de la Deutsche Forschungsgemeinschaft (DFG – Fondation Allemande pour la Recherche) à travers le projet DA 2107/1-1 et de la Max-Planck-Gesellschaft (MPG – Société Max Planck).

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Deutsche Forschungsgemeinschaft [DA 2107/1–1].

Appendix A.

Expressions analytiques des fonctions du noyau

Dans cette Annexe, nous fournissons des expressions des fonctions noyau $K_{ij}(r,t)$, pour $i,j=1,\dots ,6$, apparaissant dans le système d’équations intégrales énoncé par Equation (25)(25) $\sum _{j=1}^6{\int }_0^R{K}_{ij}(r,t){\mathcal{G}}_j(t)\mathrm{d}t={\mathrm{\Xi }}_i(r),i=1,\dots ,6,$(25) du corps principal de l’article. Elles sont donnés sous forme de matrice $6\times 6$. Nous avons

(A1) $K=\left(\begin{array}{cccccc}0& K_a& K_b& K_c& K_d& K_e\\ K_c& -K_d& -K_e& 0& -K_a& -K_b\\ K_f& 0& 0& K_g& K_h& K_i\\ -K_g& K_h& K_i& -K_f& 0& 0\\ 0& K_j& K_k& K_l& K_m& K_n\\ K_l& -K_m& -K_n& 0& -K_j& -K_k\end{array}\right).$(A1)

Les éléments non nuls de la matrice noyau sont des fonctions de $r$ et $t$. Ils peuvent être exprimés en termes d’intégrales impropres convergentes sur le nombre d’onde $\lambda$ tels que

(A2) $K_a=\frac{3}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{-\frac{1}{2}}{J}_0\left(\lambda r\right)J_{\frac{1}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A2)

(A3) $K_b=-\frac{1}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{-\frac{1}{2}}{J}_0\left(\lambda r\right)J_{\frac{5}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A3)

(A4) $K_f=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\lambda }^{-\frac{1}{2}}{J}_1\left(\lambda r\right)J_{\frac{3}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A4)

(A5) $K_j=-\frac{1}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{-\frac{1}{2}}{J}_2\left(\lambda r\right)J_{\frac{1}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A5)

(A6) $K_k=\frac{3}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{-\frac{1}{2}}{J}_2\left(\lambda r\right)J_{\frac{5}{2}}\left(\lambda t\right)\mathrm{d}\lambda .$(A6)

Comme nous le montrerons dans la suite, les intégrales infinies données par Equations (A2) à (A6) peuvent être exprimées sous forme de fonctions analytiques. De plus, nous définissons

(A7) $K_c=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\lambda }^{\frac{1}{2}}{e}^{-\lambda }{J}_0\left(\lambda r\right)J_{\frac{3}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A7)

(A8) $K_l=\frac{1}{2}{\int }_0^{\mathrm{\infty }}{\lambda }^{\frac{1}{2}}{e}^{-\lambda }{J}_2\left(\lambda r\right)J_{\frac{3}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A8)

(A9) $K_h=-\frac{1}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{\frac{1}{2}}{e}^{-\lambda }{J}_1\left(\lambda r\right)J_{\frac{1}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A9)

(A10) $K_i=-\frac{1}{4}{\int }_0^{\mathrm{\infty }}{\lambda }^{\frac{1}{2}}{e}^{-\lambda }{J}_1\left(\lambda r\right)J_{\frac{5}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A10)

ensemble avec

(A11) $K_e=\frac{1}{4}{\int }_0^{\mathrm{\infty }}\left({\lambda }^{\frac{1}{2}}+{\lambda }^{-\frac{1}{2}}\right)e^{-\lambda }{J}_0(\lambda r)J_{\frac{5}{2}}(\lambda t)\mathrm{d}\lambda ,$(A11)

(A12) $K_m=\frac{1}{4}{\int }_0^{\mathrm{\infty }}\left({\lambda }^{\frac{1}{2}}+{\lambda }^{-\frac{1}{2}}\right)e^{-\lambda }{J}_2\left(\lambda r\right)J_{\frac{1}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A12)

(A13) $K_g=-\frac{1}{2}{\int }_0^{\mathrm{\infty }}\left({\lambda }^{\frac{1}{2}}+{\lambda }^{-\frac{1}{2}}\right)e^{-\lambda }{J}_1(\lambda r)J_{\frac{3}{2}}(\lambda t)\mathrm{d}\lambda ,$(A13)

(A14) $K_n=\frac{1}{4}{\int }_0^{\mathrm{\infty }}\left({\lambda }^{\frac{1}{2}}-3{\lambda }^{-\frac{1}{2}}\right)e^{-\lambda }{J}_2\left(\lambda r\right)J_{\frac{5}{2}}\left(\lambda t\right)\mathrm{d}\lambda ,$(A14)

(A15) $K_d=\frac{1}{4}{\int }_0^{\mathrm{\infty }}\left({\lambda }^{\frac{1}{2}}-3{\lambda }^{-\frac{1}{2}}\right)e^{-\lambda }{J}_0(\lambda r)J_{\frac{1}{2}}(\lambda t)\mathrm{d}\lambda .$(A15)

La présence de la fonction exponentielle dans les intégrandes des Equations (A7) à (A15) empêche une évaluation directe de ces intégrales infinies. Par conséquent, nous utilisons des concepts d’analyses complexes pour évaluer ces intégrales analytiquement. Pour référence future, nous fournissons la représentation intégrale suivante

(A16) $\frac{sin(\lambda t)}{\lambda }={\int }_0^{t}cos(\lambda u)\mathrm{d}u,$(A16)

(A17) $\frac{cos(\lambda t)}{\lambda }=\frac{1}{\lambda }-{\int }_0^{t}sin(\lambda u)\mathrm{d}u,$(A17)

(A18) $\frac{sin(\lambda t)}{{\lambda }^2}=\frac{t}{\lambda }-{\int }_0^t{\int }_0^{u}sin(\lambda v)\mathrm{d}v\mathrm{d}u,$(A18)

(A19) $\frac{cos(\lambda t)}{{\lambda }^2}=\frac{1}{{\lambda }^2}-{\int }_0^t{\int }_0^{u}cos(\lambda v)\mathrm{d}v\mathrm{d}u,$(A19)

(A20) $\frac{sin(\lambda t)}{{\lambda }^3}=\frac{t}{{\lambda }^2}-{\int }_0^t{\int }_0^u{\int }_0^{v}cos(\lambda w)\mathrm{d}w\mathrm{d}v\mathrm{d}u.$(A20)

De plus, nous utiliserons les expressions des fonctions de Bessel de première espèce,

(A21) $J_{\frac{1}{2}}(\vartheta )={\left(\frac{2}{\pi \vartheta }\right)}^{\frac{1}{2}}sin(\vartheta ),$(A21)

(A22) $J_{\frac{3}{2}}(\vartheta )={\left(\frac{2}{\pi \vartheta }\right)}^{\frac{1}{2}}\left(\frac{sin(\vartheta )}{\vartheta }-cos(\vartheta )\right),$(A22)

(A23) $J_{\frac{5}{2}}(\vartheta )={\left(\frac{2}{\pi \vartheta }\right)}^{\frac{1}{2}}\left(\left(\frac{3}{{\vartheta }^2}-1\right)sin\vartheta -\frac{3}{\vartheta }cos\vartheta \right).$(A23)

A1. Expressions de $K_a$, $K_b$, $K_f$, $K_j$ et $K_k$

Nous définissons par commodité $\alpha =t/r$, ${\beta }_1={\left(\pi /\left(2t\right)\right)}^{\frac{1}{2}}$, ${\beta }_2={\left(2\pi t\right)}^{-\frac{1}{2}}$ et ${\chi }_1=arcsin\alpha$. De plus, nous désignons par $\mathrm{\Theta }(\cdot )$ la fonction pas de Heaviside.

Les expressions de $K_a$, $K_b$, $K_f$, $K_j$ et $K_k$ pour lesquelles l’intégrande n’implique pas la fonction exponentielle peuvent facilement être trouvées dans des tables mathématiques standard ou être obtenues en utilisant des systèmes de calcul formel tels que Mathematica (Wolfram, 1991). Ils sont explicitement donnés par

(A24) $K_a=\frac{3}{4}{\beta }_1\mathrm{\Theta }(t-r)+\frac{3}{2}{\beta }_2{\chi }_1\mathrm{\Theta }(r-t),$(A24)

(A25) $K_b=\frac{1}{4}{\beta }_1\left(1+\frac{3}{4}\left({\alpha }^{-2}-2\right)\right)\mathrm{\Theta }(t-r)-\frac{1}{4}{\beta }_2\left(\frac{3}{2}{\left({\alpha }^{-2}-1\right)}^{\frac{1}{2}}+\left(1-\frac{3}{2}{\alpha }^{-2}\right){\chi }_1\right)\mathrm{\Theta }(r-t),$(A25)

(A26) $K_f=\frac{1}{4}{\beta }_1{\alpha }^{-1}\mathrm{\Theta }(t-r)+\frac{1}{2}{\beta }_2\left({\alpha }^{-1}{\chi }_1-{\left(1-{\alpha }^2\right)}^{\frac{1}{2}}\right)\mathrm{\Theta }(r-t),$(A26)

(A27) $K_j=-\frac{1}{2}{\beta }_2\alpha {\left(1-{\alpha }^2\right)}^{\frac{1}{2}}\mathrm{\Theta }(r-t),$(A27)

(A28) $K_k=\frac{9}{32}{\alpha }^{-2}{\beta }_1\mathrm{\Theta }(t-r)+\frac{3}{4}{\beta }_2\left(\frac{3}{4}\left({\alpha }^{-2}{\chi }_1+{\left({\alpha }^{-2}-1\right)}^{\frac{1}{2}}\left(2{\alpha }^2-1\right)\right)-2\alpha {\left(1-{\alpha }^2\right)}^{\frac{1}{2}}\right)\mathrm{\Theta }(r-t).$(A28)

A.2. Evaluation des intégrales restantes

L’idée centrale de notre approche consiste à exprimer les fonctions de Bessel de première espèce d’ordre $k+\frac{1}{2}$, $k\in \{0,1,2\}$ en termes de fonctions trigonométriques en utilisant Equations (A21)–(A23). Ensuite, en utilisant les expressions intégrales (A16)–(A20) avec la classique formule d’Euler en analyse complexe, $e^{i\vartheta }=cos\vartheta +isin\vartheta$, les intégrales infinies peuvent commodément être exprimées sous la forme de transformées de Laplace de fonctions de Bessel de première espèce. Pour cela, nous définissons

(A29) ${\mathcal{C}}_k(r,t)={\int }_0^{\mathrm{\infty }}{J}_k(\lambda r)e^{-\lambda }cos(\lambda t)\mathrm{d}\lambda ,$(A29)

(A30) ${\mathcal{S}}_k(r,t)={\int }_0^{\mathrm{\infty }}{J}_k(\lambda r)e^{-\lambda }sin(\lambda t)\mathrm{d}\lambda .$(A30)

Nous définissons en outre les abréviations ${\chi }_2=arcsin\left(\left(t+i\right)/r\right)$, ${\chi }_3=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left(r^{-1}\right)$ et ${\chi }_4={\left(1+r^2\right)}^{\frac{1}{2}}$. En définissant la variable de la transformée de Laplace $s=\left(1-it\right)/r$, on remarque aisément que

(A31) $\mathcal{L}\left\{J_k\right\}(s)=r\left({\mathcal{C}}_k(r,t)+i{\mathcal{S}}_k(r,t)\right),$(A31)

avec $\mathcal{L}$ représentant l’opérateur de transformation de Laplace. On note que (Widder, 2015)

(A32) $\mathcal{L}\left\{J_k\right\}(s)={\left(1+s^2\right)}^{-\frac{1}{2}}{\left(s+{\left(1+s^2\right)}^{\frac{1}{2}}\right)}^{-k}.$(A32)

1. Évaluation de $K_c$

En utilisant la représentation intégrale (A29), l’intégrale (A7) peut être écrite sous la forme

(A33) $K_c={\beta }_2\left(-K_c^{(1)}+t^{-1}{K}_c^{(2)}\right),$(A33)

où

(A34) $K_c^{(1)}={\mathcal{C}}_0(r,t),$(A34)

(A35) $K_c^{(2)}={\int }_0^t{\mathcal{C}}_0(r,u)\mathrm{d}u.$(A35)

En définissant les abréviations $S={\left(1+s^2\right)}^{-\frac{1}{2}}$, il résulte de Equation (A31) que $K_c^{(1)}=r^{-1}Re\left\{\mathcal{L}\left\{J_0\right\}(s)\right\}=S/r$. En définissant $f(u)=(1-iu)/r$, on obtient

(A36) $K_c^{(2)}=\frac{1}{r}Re\left\{{\int }_0^t{\left(1+f{(u)}^2\right)}^{-\frac{1}{2}}\mathrm{d}u\right\}={\chi }_2.$(A36)

En collectant les termes, Equation (A33) prend la forme simplifiée finale

(A37) $K_c={\beta }_{2}Re\left\{\frac{{\chi }_2}{t}-\frac{S}{r}\right\}.$(A37)

2. Évaluation de $K_l$

Nous définissons par commodité les abréviations ${\sigma }_k=S{\left(s+S^{-1}\right)}^{-k}$ pour $k\in \{1,2\}$ avec ${\sigma }_3=(t+i)/S$. Par analogie avec la procédure d’intégration décrite ci-dessus, Equation (A8) peut également être exprimée sous la forme

(A38) $K_l={\beta }_2\left(-K_l^{(1)}+t^{-1}{K}_l^{(2)}\right),$(A38)

où

(A39) $K_l^{(1)}={\mathcal{C}}_2(r,t)=\frac{1}{r}Re\left\{{\sigma }_2\right\},$(A39)

(A40) $K_l^{(2)}={\int }_0^t{\mathcal{C}}_2(r,u)\mathrm{d}u=\frac{1}{r}\left(Re\left\{{\sigma }_3\right\}-\frac{2t}{r}\right).$(A40)

En collectant les termes, Equatiom (A38) se simplifie en

(A41) $K_l=\frac{{\beta }_2}{r}\left(Re\left\{\frac{{\sigma }_3}{t}-{\sigma }_2\right\}-\frac{2}{r}\right).$(A41)

3. Évaluation de $K_h$

L’intégrale énoncée par (A9) a une forme simple et peut facilement être évaluée comme

(A42) $K_h=-\frac{{\beta }_2}{2}{\mathcal{S}}_1(r,t)=-\frac{{\beta }_2}{2r}\mathrm{I}\mathrm{m}\left\{{\sigma }_1\right\}.$(A42)

4. Évaluation de $K_i$

Ensuite, l’intégrale (A10) peut être exprimée sous la forme

(A43) $K_i=-K_h-\frac{3}{2t}{\beta }_2\left(K_i^{(1)}-t^{-1}{K}_i^{(2)}\right),$(A43)

où $K_h$ est exprimé par Equation (A42) et

(A44) $K_i^{(1)}={\int }_0^t{\mathcal{S}}_1(r,u)\mathrm{d}u,$(A44)

(A45) $K_i^{(2)}={\int }_0^t{\int }_0^u{\mathcal{S}}_1(r,v)\mathrm{d}v\mathrm{d}u.$(A45)

L’évaluation analytique des Equations (A44) et (A45) donne

(A46) $K_i^{(1)}=\frac{{\chi }_4}{r}-\mathrm{I}\mathrm{m}\left\{\frac{i}{S}\right\},$(A46)

(A47) $K_i^{(2)}=\alpha {\chi }_4+\frac{r}{2}\mathrm{I}\mathrm{m}\left\{\frac{s}{S}-i{\chi }_2\right\}.$(A47)

En collectant les termes, Equation (A3) prend la forme finale

(A48) $K_i=\frac{{\beta }_2}{2}\mathrm{I}\mathrm{m}\left\{\frac{{\sigma }_1}{r}+\frac{3}{t}\left(\frac{i}{S}+\frac{r}{2t}\left(\frac{s}{S}-i{\chi }_2\right)\right)\right\}.$(A48)

5. Évaluation de $K_e$

L’évaluation de l’intégrale infinie (A11) est délicate du fait de la présence de ${\lambda }^{-3}$ dans l’intégrande. On peut montrer que l’intégrale transformée peut être présentée sous la forme

(A49) $\begin{array}{cc}{K}_e& =-\frac{{\beta }_2}{2}(K_e^{(1)}+K_e^{(2)}-3t^{-1}\left(K_e^{(3)}+K_e^{(4)}\right)\\ \hspace{0.17em}& +3t^{-2}\left(K_e^{(5)}+K_e^{(6)}\right)),\end{array}$(A49)

où nous avons défini

(A50) $K_e^{(1)}={\mathcal{S}}_0(r,t),$(A50)

(A51) $K_e^{(2)}={\int }_0^t{\mathcal{C}}_0(r,u)\mathrm{d}u,$(A51)

(A52) $K_e^{(3)}={\int }_0^t{\mathcal{S}}_0(r,u)\mathrm{d}u,$(A52)

(A53) $K_e^{(4)}={\int }_0^t{\int }_0^u{\mathcal{C}}_0(r,v)\mathrm{d}v\mathrm{d}u,$(A53)

(A54) $K_e^{(5)}={\int }_0^t{\int }_0^u{\mathcal{S}}_0(r,v)\mathrm{d}v\mathrm{d}u,$(A54)

(A55) $K_e^{(6)}={\int }_0^t{\int }_0^u{\int }_0^v{\mathcal{C}}_0(r,w)\mathrm{d}w\mathrm{d}v\mathrm{d}u.$(A55)

Ces dernières intégrales peuvent être évaluées analytiquement. Ils sont donnés par

(A56) $K_e^{(1)}=\frac{1}{r}\mathrm{I}\mathrm{m}\left\{S\right\},$(A56)

(A57) $K_e^{(2)}=\mathrm{R}\mathrm{e}\left\{{\chi }_2\right\},$(A57)

(A58) $K_e^{(3)}=\mathrm{I}\mathrm{m}\left\{{\chi }_2\right\}-{\chi }_3,$(A58)

(A59) $K_e^{(4)}={\mathrm{\Phi }}_2+\mathrm{R}\mathrm{e}{\mathrm{\Phi }}_1,$(A59)

(A60) $K_e^{(5)}=\mathrm{I}\mathrm{m}\{{\mathrm{\Phi }}_1\}-t{\chi }_3,$(A60)

(A61) $K_e^{(6)}=t{\mathrm{\Phi }}_2+\frac{1}{4}\mathrm{R}\mathrm{e}\left\{{\chi }_2{\mathrm{\Lambda }}_1+3r{\sigma }_3\right\},$(A61)

avec ${\mathrm{\Phi }}_1=(t+i){\chi }_2+r/S$ et ${\mathrm{\Phi }}_2={\chi }_3-{\chi }_4$. De plus, ${\mathrm{\Lambda }}_1=r^2+2t^2-2+4it$. En rassemblant les résultats, l’intégrale (A11) peut être évaluée telle que

(A62) $K_e=\frac{{\beta }_2}{8}\mathrm{R}\mathrm{e}\left\{\frac{3r{\sigma }_3}{t^2}-{\chi }_2\left(\frac{3}{{\alpha }^2}+\frac{6}{t^2}-2\right)+\frac{4iS}{r}\right\}.$(A62)

6. Évaluation de $K_m$

Nous procédons suivant une approche analogue et exprimons l’intégrale (A12) comme

(A63) $K_m=\frac{{\beta }_2}{2}\left(K_m^{(1)}+K_m^{(2)}\right),$(A63)

où nous avons défini

(A64) $K_m^{(1)}={\mathcal{S}}_2(r,t)=\frac{1}{r}\mathrm{I}\mathrm{m}\left\{{\sigma }_2\right\},$(A64)

(A65) $K_m^{(2)}={\int }_0^t{\mathcal{C}}_2(r,u)\mathrm{d}u=\frac{1}{r}\left(\mathrm{R}\mathrm{e}\left\{{\sigma }_3\right\}-2\alpha \right).$(A65)

La combinaison des résultats nous amène à

(A66) $K_m=\frac{{\beta }_2}{2r}\left(\mathrm{R}\mathrm{e}\left\{{\sigma }_3\right\}+\mathrm{I}\mathrm{m}\left\{{\sigma }_2\right\}-2\alpha \right).$(A66)

7. Évaluation de $K_g$

L’intégrale (A13) peut être exprimée sous la forme

(A67) $K_g={\beta }_2\left(K_g^{(1)}-K_g^{(2)}-t^{-1}\left(K_g^{(3)}-K_g^{(4)}\right)\right),$(A67)

où nous avons défini

(A68) $K_g^{(1)}={\mathcal{C}}_1(r,t),$(A68)

(A69) $K_g^{(2)}={\int }_0^t{\mathcal{S}}_1(r,u)\mathrm{d}u,$(A69)

(A70) $K_g^{(3)}={\int }_0^t{\mathcal{C}}_1(r,u)\mathrm{d}u,$(A70)

(A71) $K_g^{(4)}={\int }_0^t{\int }_0^u{\mathcal{S}}_1(r,v)\mathrm{d}v\mathrm{d}u.$(A71)

L’évaluation de ces intégrales donne

(A72) $K_g^{(1)}=\frac{1}{r}\left(1-\mathrm{R}\mathrm{e}\left\{sS\right\}\right),$(A72)

(A73) $K_g^{(2)}=\frac{{\chi }_4}{r}-\mathrm{R}\mathrm{e}\left\{S^{-1}\right\},$(A73)

(A74) $K_g^{(3)}=\alpha +\mathrm{I}\mathrm{m}\left\{S^{-1}\right\},$(A74)

(A75) $K_g^{(4)}=\alpha {\chi }_4+\frac{r}{2}\mathrm{I}\mathrm{m}\left\{s{S}^{-1}-i{\chi }_2\right\}.$(A75)

Enfin, on obtient

(A76) $K_g=\frac{{\beta }_2}{t}Re\left\{{\sigma }_3-\frac{r{\chi }_2}{2}-\frac{irs}{2S}-\alpha sS\right\}.$(A76)

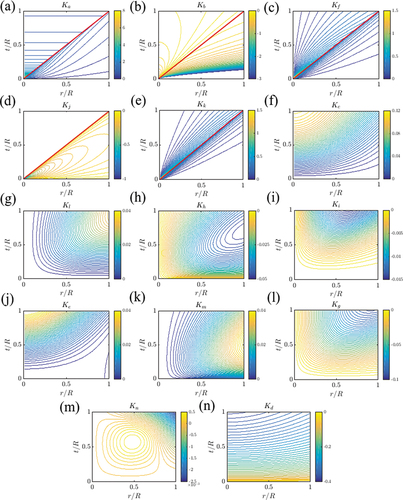
Figure A1. Tracés de contour des fonctions du noyau données par Equations (A2) à (A15). Les lignes rouges dans les sous-figures (a) à (e) correspondent à la première bissectrice.

8. Évaluation de $K_n$

L’intégrale (A14) peut être exprimée comme

(A77) $\begin{array}{cc}{K}_n& =-\frac{{\beta }_2}{2}(K_n^{(1)}-3K_n^{(2)}-3t^{-1}\left(K_n^{(3)}-3K_n^{(4)}\right)\\ \hspace{0.17em}& +3t^{-2}\left(K_n^{(5)}-3K_n^{(6)}\right)),\end{array}$(A77)

où $K_n^{(1)}=K_m^{(1)}$ et $K_n^{(2)}=K_m^{(2)}$. En plus,

(A78) $K_n^{(3)}={\int }_0^t{\mathcal{S}}_2(r,u)\mathrm{d}u,$(A78)

(A79) $K_n^{(4)}={\int }_0^t{\int }_0^u{\mathcal{C}}_2(r,v)\mathrm{d}v\mathrm{d}u,$(A79)

(A80) $K_n^{(5)}={\int }_0^t{\int }_0^u{\mathcal{S}}_2(r,v)\mathrm{d}v\mathrm{d}u,$(A80)

(A81) $K_n^{(6)}={\int }_0^t{\int }_0^u{\int }_0^v{\mathcal{C}}_2(r,w)\mathrm{d}w\mathrm{d}v\mathrm{d}u.$(A81)

L’évaluation des intégrales (A78) à (A81) nous amène à

(A82) $K_n^{(3)}={\alpha }^2-\frac{{\chi }_4}{r^2}+\frac{1}{r}\mathrm{I}\mathrm{m}\left\{{\sigma }_3\right\},$(A82)

(A83) $K_n^{(4)}=\frac{{\chi }_4^3}{3r^2}-{\alpha }^2-\frac{r}{3}\mathrm{R}\mathrm{e}\left\{S^{-3}\right\},$(A83)

(A84) $K_n^{(5)}=\frac{{\alpha }^{2}t}{3}-\frac{t{\chi }_4}{r^2}-\frac{r}{3}\mathrm{I}\mathrm{m}\left\{S^{-3}\right\},$(A84)

(A85) $K_n^{(6)}=\frac{t{\chi }_4^3}{3r^2}-\frac{{\alpha }^{2}t}{3}-\frac{r}{8}\mathrm{R}\mathrm{e}\left\{r{\chi }_2+{\sigma }_3{\mathrm{\Lambda }}_2\right\},$(A85)

avec ${\mathrm{\Lambda }}_2=1+2{\left(3S^2\right)}^{-1}$. Mettre les résultats ensemble donne

(A86) $K_n={\beta }_2\left(\frac{\alpha }{r}+\frac{3}{16}Re\left\{{\mathrm{\Psi }}_1\right\}+\frac{1}{2r}Im\left\{{\mathrm{\Psi }}_2\right\}\right),$(A86)

où

(A87) ${\mathrm{\Psi }}_1=\frac{6}{\alpha S^3}-\frac{\left(3{\alpha }^{-2}-8\right)}{r}{\sigma }_3-\frac{3{\chi }_2}{{\alpha }^2},$(A87)

(A88) ${\mathrm{\Psi }}_2=\frac{7}{4{\alpha }^2{S}^3}+\frac{3{\sigma }_3}{\alpha r}-{\sigma }_2.$(A88)

9. Évaluation de $K_d$

Enfin, l’intégrale (A15) peut s’écrire sous la forme

(A89) $K_d=\frac{{\beta }_2}{2}\left(K_e^{(1)}-3K_e^{(2)}\right),$(A89)

où $K_e^{(1)}$ et $K_e^{(2)}$ ont été précédemment définis par Equations (A50) et (A51), respectivement. On obtient

(A90) $K_d=\frac{{\beta }_2}{2}\left(\frac{1}{r}\mathrm{I}\mathrm{m}\left\{S\right\}-3\mathrm{R}\mathrm{e}\left\{{\chi }_2\right\}\right).$(A90)

Nous présentons dans Figure A1 les courbes de niveau des fonctions noyaux dans le plan $(r/R,t/R)$.

Appendix B.

Test d’indépendance de la grille

Figure B1. Erreur de quadrature dans l’évaluation de la vitesse d’écoulement par rapport au nombre de nœuds dans la quadrature de Legendre Gauss. La légende montre les coordonnées des trois points représentatifs dans le champ d’écoulement. Ici, les différents paramètres sont $M=10N,R=1$ et $h=0,25$.

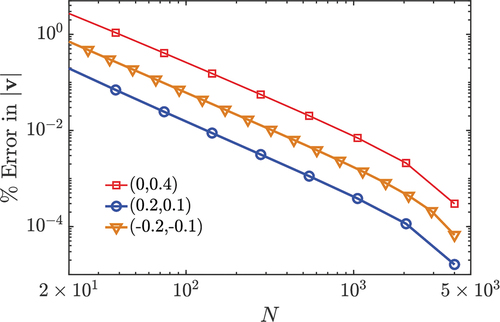
Ici, la seule source d’erreur numérique provient de l’approximation d’intégration utilisant une règle de quadrature. Des expériences numériques suggèrent qu’un nombre suffisamment grand de points de quadrature est nécessaire pour obtenir la précision numérique souhaitée. Afin d’estimer les erreurs dans la solution numérique, nous calculons le champ de vitesse pour un nombre croissant de points de quadrature, $N$, et observons l’erreur relative de calcul par rapport à une taille de grille plus fine pour $N=5000$ et $M=10N$. Ces observations sont résumées dans Figure A1 pour trois points représentatifs dans le champ d’écoulement. Un ajustement linéaire montre que l’erreur de calcul diminue avec $N$ comme $N^{-3/2}$. Notamment, l’erreur reste inférieure à 10⁻³% pour $N\ge 4000$. Sauf indication contraire, nous prenons dans ce manuscrit au nombre minimum de points de collocation $N=3000$ et fixons systématiquement $M=10N$.