γ-fuzzy filters and space of γ -- fuzzy filters in P-algebra

ABSTRACT

In this paper, we introduce the concept of $\gamma -\text{fuzzy}$ filters in a pseudo-complemented distributive lattices. We study the special class of fuzzy filters called $\gamma -\text{fuzzy}$ filters, which is isomorphic to the set of all fuzzy ideals of the lattice of boosters. We observe that every $\gamma -\text{fuzzy}$ filters is the intersection of all prime $\gamma -\text{fuzzy}$ filters containing it. We also topologize the set of all prime $\gamma -\text{fuzzy}$ filters of a pseudo-completed distributive lattice. Properties of the space also studied. We show that there is a one to one correspondence between the class of $\gamma -\text{fuzzy}$ filters and the lattice of all open sets in ${\mathcal{P}}_{\gamma }$. It is proved that the space ${\mathcal{P}}_{\gamma }$ is a T₀ space.

KEYWORDS:

• pseudo-complemented distributive lattice
• fuzzy ideal
• fuzzy filter

MATHEMATICS SUBJECT CLASSIFICATION:

• 06D72
• 08A72
• 03E72

1. Introduction

Classical set theory is based on the fundamental concept of a set, in which individuals are either a member or not a member. A sharp, crisp, and unambiguous distinction exists between a member and a non-member for any well-defined set of entities in this theory, and there is a very precise and clear boundary to indicate if an entity belongs to a set or not. Thus, in classical set theory an element is not allowed to be in a set or not in a set at the same time. This means that many real-world problems cannot be handled by classical set theory. Many of the collections and categories we commonly employ, however, do not exhibit this characteristic. Instead their boundaries seem vague, and the transition from member to nonmember appears gradual rather than abrupt. Thus fuzzy set introduces vagueness by eliminating the sharp boundary dividing members of the class from nonmembers. Real situations are very often not crisp and deterministic and they can not be described precisely. Such situations in our real life which are characterized by vagueness or imprecision can not be answered just in yes or no. In 1965 (Zadeh, 1965) mathematically formulated the fuzzy subset concept. He defined fuzzy subset of a non-empty set as a collection of objects with grade of membership in a continuum, with each object being assigned a value between 0 and 1 by a membership function. In 1971, A. Rosenfeld used the notion of a fuzzy subset of a set to introduce the notion of a fuzzy subgroup of a group (Rosenfeld, 1971) and his paper inspired the development of fuzzy abstract algebra. Since then, several authors have developed interesting results on fuzzy theory; see (Abou-Zaid, 1993; Addis & Engidaw, 2020; Ajmal & Thomas, 1994; Alemayehu & Wondifraw, 2021; Asaad, 1991; Liu, 1982; Muhiuddin et al., 2021; Norahun & Dvorák, 2020; Norahun & Zeleke, 2021; Yuan & Wu, 1990).

The theory of pseudo-complementation was introduced and extensively studied in semi-lattices and particularly in distributive lattices by (Frink, 1962) and (Birkhoff, 1948). Later, pseudo-complement in Stone algebra has been studied by several authors like (Balbes & Horn, 1970), G. Gr$\ddot{a}$tzer (Frink, 1963) etc. In (Badawy, 2016), A. E. Badawy studied the concept of filters of p-algebras with respect to a closure operator. Motivated by Badawy’s work, in this paper, we study the fuzzy aspect of $\gamma -\text{fuzzy}$ filters in a p-algebra.

In this paper, we introduce the concept of $\gamma -\text{fuzzy}$ filters in pseudo-complemented distributive lattice. Basic properties of $\gamma -\text{fuzzy}$ filters also investigated. We observe that there is a homomorphism mapping between the class of all fuzzy filters and the class of all fuzzy ideals of the boosters. We also study the special class of fuzzy filters called $\gamma -\text{fuzzy}$ filters. We prove that these fuzzy filters forms a complete distributive lattice and isomorphic to the set of fuzzy ideals of the lattice of boosters $B_{\ast }(L)$. Furthermore, we show that there is a one to one correspondence between the class of prime $\gamma -\text{fuzzy}$ filters of a p-algebra L and the set of all prime ideals of $B_{\ast }(L)$. We observe that every $\gamma -\text{fuzzy}$ filter is the intersection of all prime $\gamma -\text{fuzzy}$ filters containing it. We give the definition of prime fuzzy filter using the concept of fuzzy points. Moreover, we study the space of all prime $\gamma -\text{fuzzy}$ filters in a pseudo-complemented distributive lattice. The set of prime $\gamma -\text{fuzzy}$ filters of L is denoted by ${\mathcal{P}}_{\gamma }$. For a $\gamma -\text{fuzzy}$ filter ν of L, open subset of ${\mathcal{P}}_{\gamma }$ is of the form $\mathcal{P}(\nu )=\{\lambda \in {\mathcal{P}}_{\gamma }:\nu ⊈\lambda \}$ and $\mathrm{\Gamma }(\nu )=\{\lambda \in {\mathcal{P}}_{\gamma }:\nu \subseteq \lambda \}$ is a closed set. We also show that the set of all open sets of the form $\mathcal{P}(a_{\alpha })=\{\lambda \in {\mathcal{P}}_{\gamma }:a_{\alpha }⊈\lambda ,a\in L,\alpha \in (0,1]\}$ forms a basis for the open sets of ${\mathcal{P}}_{\gamma }$. Finally, we observe that there is a one to one correspondence between the class of all $\gamma -\text{fuzzy}$ filters of L and the lattice of all open sets of prime $\gamma -\text{fuzzy}$ filters ${\mathcal{P}}_{\gamma }$.

2. Preliminaries

We refer (Badawy, 2016; Birkhoff, 1948) for the elementary concepts of lattices and γ-filters of a pseudo-complemented distributive lattice. We also take a reference (Swamy & Raju, 1998; Zadeh, 1965), for the elementary concepts of fuzzy set theory and fuzzy ideals of a lattice.

An algebra $L=(L;\wedge ,\vee ,\ast ,0,1)$ is of type $(2,2,1,0,0)$ is a pseudo-complemented distributive lattice , if the following conditions hold:

(1)	$(L;\wedge ,\vee ,0,1)$ is a bounded distributive lattice,
(2)	for all $a,b\in L,a\wedge b=0\iff a\wedge b^{\ast }=a$.

Definition 2.1.

(Badawy, 2016) Let L be a pseudo-complemented distributive lattice. Then for any $a\in L$, define the booster of a as follows:

$\begin{array}{l}(a{)}^{+}=\{x\in L:a\le x^{\ast \ast }\}.\end{array}$

Then it can be easily observed that $(a{)}^{+}$ is a filter of L containing a.

The set of all boosters of a pseudo-complemented lattice is denoted by $B_{\ast }(L)$. (Badawy, 2016).

Lemma 2.2.

For any $x,y\in L$, the following conditions hold.

(1)	$(x{)}^{+}=(x^{\ast \ast }{)}^{+}$
(2)	$x\le y\Rightarrow (y{)}^{+}\subseteq (x{)}^{+}$
(3)	$(x\vee y{)}^{+}=(x{)}^{+}\cap (y{)}^{+}$
(4)	$(x{)}^{+}=L$ if and only if x=0.

Definition 2.3.

(Swamy & Raju, 1998) A fuzzy subset µ of a lattice L is called a fuzzy ideal of L if, for all $x,y\in L$ the following condition satisfies:

(1)	$\mu (0)=1$
(2)	$\mu (x\vee y)\ge \mu (x)\wedge \mu (y)$
(3)	$\mu (x\wedge y)\ge \mu (x)\vee \mu (y)$

Definition 2.4.

(Swamy & Raju, 1998) A fuzzy subset µ of a lattice L is called a fuzzy filter of L if, for all $x,y\in L$ the following condition satisfies:

(1)	$\mu (1)=1$
(2)	$\mu (x\vee y)\ge \mu (x)\vee \mu (y)$
(3)	$\mu (x\wedge y)\ge \mu (x)\wedge \mu (y)$

The set of all fuzzy filters of L is denoted by FF(L).

Let µ be a fuzzy subset of a lattice L. The smallest fuzzy filter of L containing µ is called a fuzzy filter of L induced by µ and denoted by $[\mu )$ and

$\begin{array}{l}[\mu )=\bigcap \{\theta \in FF(L):\mu \subseteq \theta \}.\end{array}$

The binary operations ”+” and “·” on the set of all fuzzy subsets of a distributive lattice L as:

$\begin{array}{ll}(\mu +\theta )(x)=& Sup\{\mu (y)\wedge \theta (z):y,z\in L,y\vee z=x\}\mathrm{and}\\ (\mu \cdot \theta )(x)=& Sup\{\mu (y)\wedge \theta (z):y,z\in L,y\wedge z=x\}.\end{array}$

If µ and θ are fuzzy ideals of L, then $\mu \cdot \theta =\mu \wedge \theta =\mu \cap \theta$ and $\mu +\theta =\mu \vee \theta$.

If µ and θ are fuzzy filters of L, then $\mu +\theta =\mu \wedge \theta$ and $\mu \cdot \theta =\mu \vee \theta$

Lemma 2.5.

(Alaba & Norahun, 2018) For any two fuzzy subsets µ and θ of a distributive lattice L, we have

$\begin{array}{l}(\mu \cdot \theta ]=(\mu ]\wedge (\theta ].\end{array}$

The above result works dually, that is

For any two fuzzy subsets µ and θ of a distributive lattice L, we have

$\begin{array}{l}[\mu +\theta )=[\mu )\wedge [\theta ).\end{array}$

3. $\gamma -\text{fuzzy}$ filters

In this section, we introduce the concept of $\gamma -\text{fuzzy}$ filters in a pseudo-complemented distributive lattice. We study some basic properties of the class of $\gamma -\text{fuzzy}$ filters. We prove that the class of $\gamma -\text{fuzzy}$ filters forms a complete distributive lattice and isomorphic to the class of fuzzy filters of $B_{\ast }(L)$. We also show that there is a one to one correspondence between the set of all prime $\gamma -\text{fuzzy}$ filters of L and prime fuzzy ideals of $B_{\ast }(L)$. Finally, we observe that every $\gamma -\text{fuzzy}$ filters is the intersection of all prime $\gamma -\text{fuzzy}$ filters containing it.

Throughout the rest of this paper L stands for a pseudo-complemented distributive lattice unless otherwise mentioned.

Theorem 3.1.

For any fuzzy filter η of L, the fuzzy subset $\gamma (\eta )$ of $B_{\ast }(L)$ defined by:

$\begin{array}{l}\gamma (\eta )((a{)}^{+})=Sup\{\eta (b):(b{)}^{+}=(a{)}^{+},b\in L\}\end{array}$

is a fuzzy ideal of $B_{\ast }(L)$.

Proof.

Let η be a fuzzy filter of L. Then it can be easily verified that $\gamma (\eta )((1{)}^{+})=1$. Now, for any $(x{)}^{+},(y{)}^{+}\in B_{\ast }(L)$,

$\begin{array}{lll}\gamma (\eta )((x{)}^{+})\wedge \gamma (\eta )((y{)}^{+})& =& Sup\{\eta (a):(a{)}^{+}=(x{)}^{+},a\in L\}\\ & & \wedge Sup\{\eta (b):(b{)}^{+}=(y{)}^{+},b\in L\}\\ & \le & Sup\{\eta (a\wedge b):(a{)}^{+}\underset{―}{\vee }(b{)}^{+}=(x{)}^{+}\underset{―}{\vee }(y{)}^{+}\}\\ & =& Sup\{\eta (a\wedge b):(a\wedge b{)}^{+}=(x\wedge y{)}^{+}\}\\ & \le & Sup\{\eta (c):(c{)}^{+}=(x\wedge y{)}^{+}\}\\ & =& \gamma (\eta )((x{)}^{+}\underset{―}{\vee }(y{)}^{+})\end{array}$

Thus, $\gamma (\eta )((x{)}^{+}\underset{―}{\vee }(y{)}^{+})\ge \gamma (\eta )((x{)}^{+})\wedge \gamma (\eta )((y{)}^{+})$.

On the other hand,

$\begin{array}{lll}\gamma (\eta )((x{)}^{+})& =& Sup\{\eta (a):(a{)}^{+}=(x{)}^{+}\}\\ & \le & Sup\{\eta (a\vee y):(a{)}^{+}\wedge (y{)}^{+}=(x{)}^{+}\wedge (y{)}^{+}\}\\ & \le & Sup\{\eta (c):(c{)}^{+}=(x\vee y{)}^{+}\}\\ & =& \gamma (\eta )((x{)}^{+}\cap (y{)}^{+})\end{array}$

This shows that $$\begin{gathered} \gamma (\eta )((x{)}^{+}\cap (y{)}^{+})\ge \gamma (\eta )((x{)}^{+})\vee \gamma (\eta ) \\ ((y{)}^{+}) \end{gathered}$$. Hence $\gamma (\theta )$ is a fuzzy ideal of $B_{\ast }(L)$.

Lemma 3.2.

Let λ be a fuzzy ideal of $B_{\ast }(L)$. Then the fuzzy subset $\overleftarrow{\gamma }(\lambda )$ of L defined as $\overleftarrow{\gamma }(\lambda )(a)=\lambda ((a{)}^{+})$ is a fuzzy filter of L.

Proof.

Since $(1{)}^{+}$ is the smallest element of $B_{\ast }(L)$, we get $\overleftarrow{\gamma }(\lambda )(1)=1$. For any $a,b\in L$,

$\begin{array}{l}\overleftarrow{\gamma }(\lambda )(a\wedge b)=\lambda ((a{)}^{+})\underset{―}{\vee }\lambda ((b{)}^{+})=\overleftarrow{\gamma }(\lambda )(a)\wedge \overleftarrow{\gamma }(\lambda )(b).\end{array}$

Thus $\overleftarrow{\gamma }(\lambda )$ is a fuzzy filter of L.

Lemma 3.3.

If λ and ν are fuzzy filters of L, then $\lambda \subseteq \nu$ implies $\gamma (\lambda )\subseteq \gamma (\nu )$.

Lemma 3.4.

If $\lambda ,\nu$ are fuzzy ideals of $B_{\ast }(L)$, then $\lambda \subseteq \nu$ implies $\overleftarrow{\gamma }(\lambda )\subseteq \overleftarrow{\gamma }(\nu )$.

Theorem 3.5.

The set $FI(B_{\ast }(L))$ of all fuzzy ideals of $B_{\ast }(L)$ forms a complete distributive lattice, where the infimum and supremum of any family $\{{\lambda }_j:j\in J\}$ of fuzzy ideals is given by:

$\begin{array}{l}\bigwedge {\lambda }_j=\bigcap {\lambda }_{j}and\bigvee {\lambda }_j=(\bigcup {\lambda }_j].\end{array}$

Theorem 3.6.

The mapping γ is a homomorphism of FF(L) into $FI(B_{\ast }(L))$.

Proof.

Let $\lambda ,\nu$ be two fuzzy filters of L. Then by Lemma 3.3, we have $\gamma (\lambda \cap \nu )\subseteq \gamma (\lambda )\cap \gamma (\nu )$ and $$\begin{gathered} \gamma (\lambda ) \\ \underset{―}{\vee }\gamma (\nu )\subseteq \gamma (\lambda \vee \nu ) \end{gathered}$$. For any $(x{)}^{+}\in B_{\ast }(L)$,

$\begin{array}{lll}\gamma (\lambda )((x{)}^{+})\wedge \gamma (\nu )((x{)}^{+})& =& Sup\{\lambda (a):(a{)}^{+}=(x{)}^{+}\}\wedge Sup\{\nu (b):(b{)}^{+}=(x{)}^{+}\}\\ & \le & Sup\{\lambda (a\vee b):(a\vee b{)}^{+}=(x{)}^{+}\}\\ & & \wedge Sup\{\nu (a\vee b):(a\vee b{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{\lambda (a\vee b)\wedge \nu (a\vee b):(a\vee b{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{(\lambda \cap \nu )(a\vee b):(a\vee b{)}^{+}=(x{)}^{+}\}\\ & \le & Sup\{(\lambda \cap \nu )(c):(c{)}^{+}=(x{)}^{+}\}\\ & =& \gamma (\lambda \cap \nu )((x{)}^{+})\end{array}$

Thus $\gamma (\lambda )\cap \gamma (\nu )=\gamma (\lambda \cap \nu )$.

And

$\begin{array}{lll}\gamma (\lambda \vee \nu )((x{)}^{+})& =& Sup\{(\lambda \vee \nu )(a):(a{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{Sup\{\lambda (y)\wedge \nu (z):a=y\wedge z\},(y\wedge z{)}^{+}=(x{)}^{+}\}\\ & \le & Sup\{Sup\{\lambda (b_1)\wedge \nu (b_2):(b_1{)}^{+}=(y{)}^{+},(b_2{)}^{+}=(z{)}^{+}\},\\ & & (y\wedge z{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{Sup\{\lambda (b_1):(b_1{)}^{+}=(y{)}^{+}\}\\ & & \wedge Sup\{\nu (b_2):(b_2{)}^{+}=(z{)}^{+}\},(y\wedge z{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{\gamma (\lambda )(y{)}^{+}\wedge \gamma (\nu )(z{)}^{+}:(y\wedge z{)}^{+}=(x{)}^{+}\}\\ & =& Sup\{\gamma (\lambda )(y{)}^{+}\wedge \gamma (\nu )(z{)}^{+}:(y{)}^{+}\underset{―}{\vee }(z{)}^{+}=(x{)}^{+}\}\\ & =& (\gamma (\lambda )\underset{―}{\vee }\gamma (\nu ))((x{)}^{+})\end{array}$

Thus $\gamma (\lambda \vee \nu )=\gamma (\lambda )\underset{―}{\vee }\gamma (\nu )$. So γ is a homomorphism.

Corollary 3.7.

For any two fuzzy filters λ and ν of L,

$\begin{array}{l}\overleftarrow{\gamma }\gamma (\lambda \cap \nu )=\overleftarrow{\gamma }\gamma (\lambda )\cap \overleftarrow{\gamma }\gamma (\nu ).\end{array}$

Lemma 3.8.

Let λ be a fuzzy ideal of $B_{\ast }(L)$. Then $\gamma \overleftarrow{\gamma }(\lambda )=\lambda$.

Proof.

Since λ is a fuzzy ideal of $B_{\ast }(L)$, by Lemma 3.2, $\overleftarrow{\gamma }(\lambda )$ is a fuzzy filter of L and $\gamma \overleftarrow{\gamma }(\lambda )$ is a fuzzy ideal of $B_{\ast }(L)$. Now, $\gamma \overleftarrow{\gamma }(\lambda )((x{)}^{+})=Sup\{\overleftarrow{\gamma }(\lambda )(a):(a{)}^{+}=(x{)}^{+}\}=Sup\{\lambda ((a{)}^{+}):(a{)}^{+}=(x{)}^{+}\}=\lambda ((x{)}^{+})$. Thus $\gamma \overleftarrow{\gamma }(\lambda )=\lambda$.

Now we define $\gamma -\text{fuzzy}$ filter.

Definition 3.9.

A fuzzy filter θ of L is called a $\gamma -\text{fuzzy}$ filter of L if $\theta =\overleftarrow{\gamma }\gamma (\theta )$.

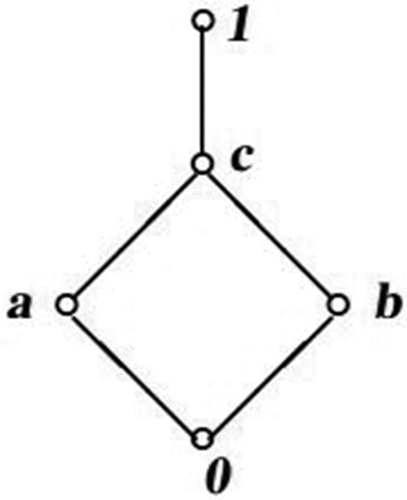
Example 3.10.

Consider the p-algebra $L=\{0,a,b,c,1\}$ whose Hasse diagram is given below.

Define fuzzy subsets λ and ν of L as follows:

$\begin{array}{l}\lambda (c)=\mu (1)=1,\lambda (a)=\lambda (b)=0.7,\lambda (0)=0.4\mathrm{and}\\ \nu (0)=0.3,\nu (b)=0.7,\nu (a)=0.8,\nu (c)=0.9,\mathrm{and}\nu (1)=1.\end{array}$

Then it can be easily verified that λ is a $\gamma -\text{fuzzy}$ filter of L. But ν is a fuzzy filter of L but not a $\gamma -\text{fuzzy}$ filter of L.

Theorem 3.11.

For a nonempty fuzzy subset θ of L , θ is a $\gamma -\text{fuzzy}$ filter if and only if each level subset of θ is a γ-filter of L.

Proof.

Let θ be a $\gamma -\text{fuzzy}$ filter of L. Then ${\theta }_t=(\overleftarrow{\gamma }\gamma (\theta ){)}_t$. To prove each level subset of θ is a γ-filter of L, it is enough to show $\overleftarrow{\gamma }\gamma ({\theta }_t)=(\overleftarrow{\gamma }\gamma (\theta ){)}_t$ for all $t\in [0,1]$. Clearly, $(\overleftarrow{\gamma }\gamma (\theta ){)}_t\subseteq \overleftarrow{\gamma }\gamma ({\theta }_t)$. Let $x\in \overleftarrow{\gamma }\gamma ({\theta }_t)$. Then $(x{)}^{+}\in \gamma ({\theta }_t)$ and there is $y\in {\theta }_t$ such that $(x{)}^{+}=(y{)}^{+}$. Which implies $Sup\{\theta (a):(a{)}^{+}=(x{)}^{+}\}\ge t$. This shows that $x\in (\overleftarrow{\gamma }\gamma (\theta ){)}_t$. Thus, ${\theta }_t=\overleftarrow{\gamma }\gamma ({\theta }_t)$ and hence each level subset of θ is a γ-filter of L.

Conversely, assume that each level subset of θ is a γ-filter. Then θ is a fuzzy filter and $\theta \subseteq \overleftarrow{\gamma }\gamma (\theta )$. Let $t=\overleftarrow{\gamma }\gamma (\theta )(x)=Sup\{\theta (y):(y{)}^{+}=(x{)}^{+}\}$. Then for each ϵ > 0, there is $a\in L$ such that $(a{)}^{+}=(x{)}^{+}$ and $\theta (a)>t-ϵ$.

$\begin{array}{lll}& \Rightarrow & a\in {\theta }_{t-ϵ},(a{)}^{+}=(x{)}^{+}\\ & \Rightarrow & x\in \overleftarrow{\gamma }\gamma ({\theta }_{t-ϵ})={\theta }_{t-ϵ}\\ & \Rightarrow & x\in \bigcap _{ϵ>0}{\theta }_{t-ϵ}={\theta }_t\\ & \Rightarrow & x\in {\theta }_t\\ & \Rightarrow & \theta (x)\ge t\\ & \Rightarrow & \overleftarrow{\gamma }\gamma (\theta )(x)\subseteq \theta (x)\end{array}$

Thus $\overleftarrow{\gamma }\gamma (\theta )\subseteq \theta$ and hence θ is a $\gamma -\text{fuzzy}$ filter of L.

Corollary 3.12.

For a nonempty subset F of L, F is a γ-filter if and only if χ_F is a $\gamma -\text{fuzzy}$ filter of L.

Theorem 3.13.

Let λ be a fuzzy filter of L. Then λ is a $\gamma -\text{fuzzy}$ filter if and only if for each $a,b\in L,(a{)}^{+}=(b{)}^{+}$ imply $\lambda (a)=\lambda (b)$.

Lemma 3.14.

Let λ be a $\gamma -\text{fuzzy}$ filter of L. Then $\lambda (a)=\lambda (a^{\ast \ast })$ for all $a\in L$.

Proof.

Let λ be a $\gamma -\text{fuzzy}$ filter of L. For any $a\in L$, we know that $(a{)}^{+}=(a^{\ast \ast }{)}^{+}$. Thus, by Theorem 3.13, we get that $\lambda (a)=\lambda (a^{\ast \ast })$.

Lemma 3.15.

For any fuzzy filter λ of L, the map $\lambda ⟶\overleftarrow{\gamma }\gamma (\lambda )$ is a closure operator on FF(L). That is.

(1)	$\lambda \subseteq \overleftarrow{\gamma }\gamma (\lambda )$
(2)	$\overleftarrow{\gamma }\gamma (\overleftarrow{\gamma }\gamma (\lambda ))=\overleftarrow{\gamma }\gamma (\lambda )$
(3)	$\lambda \subseteq \nu \Rightarrow \overleftarrow{\gamma }\gamma (\lambda )\subseteq \overleftarrow{\gamma }\gamma (\nu )$ for any two fuzzy filters $\lambda ,\nu$ of L

$\gamma -\text{fuzzy}$ filters are simply the closed elements of FF(L) with respect to the closure operator.

Let us denote the set of all $\gamma -\text{fuzzy}$ filters of L by $F{F}_{\gamma }(L)$.

Lemma 3.16.

If $\lambda ,\nu \in F{F}_{\gamma }(L)$, then the supremum of λ and ν is given by:

$\begin{array}{l}\lambda \underset{―}{\vee }\nu =\overleftarrow{\gamma }\gamma (\lambda \vee \nu ).\end{array}$

Proof.

Clearly $\lambda \underset{―}{\vee }\nu$ is a $\gamma -\text{fuzzy}$ filter of L. Now we proceed to show that $\lambda \underset{―}{\vee }\nu$ is the least upper bound of $\{\lambda ,\nu \}$. Since $\lambda ,\nu \subseteq \lambda \vee \nu \subseteq \lambda \underset{―}{\vee }\nu$, $\lambda \underset{―}{\vee }\nu$ is an upper bound of $\{\lambda ,\nu \}$. Let η be any upper bound for $\lambda ,\nu$ in $F{F}_{\gamma }(L)$. Then $\lambda \vee \nu \subseteq \eta$. Which implies that $\overleftarrow{\gamma }\gamma (\lambda \vee \nu )\subseteq \overleftarrow{\gamma }\gamma (\eta )=\eta$. Therefore, $\overleftarrow{\gamma }\gamma (\lambda \vee \nu )$ is the supremum of both $\{\lambda ,\nu \}$ in $F{F}_{\gamma }(L)$.

Theorem 3.17.

The class $F{F}_{\gamma }(L)$ of all γ-fuzzy filters of L forms a complete distributive lattice with respect to set inclusion.

Proof.

Clearly $(F{F}_{\gamma }(L),\subseteq )$ is a partially ordered set. For $\lambda ,\nu \in F{F}_{\gamma }(L)$, define

$\begin{array}{l}\lambda \wedge \nu =\lambda \cap \nu \mathrm{and}\lambda \underset{―}{\vee }\nu =\overleftarrow{\gamma }\gamma (\lambda \vee \nu ).\end{array}$

Then clearly $\lambda \wedge \nu ,\lambda \underset{―}{\vee }\nu \in F{F}_{\gamma }(L)$. Hence $(F{F}_{\gamma }(L),\wedge ,\underset{―}{\vee })$ is a lattice.

We now prove the distributivity. Let $\eta ,\nu ,\lambda \in F{F}_{\gamma }(L)$. Then

$\begin{array}{lll}\eta \underset{―}{\vee }(\nu \cap \lambda )& =& \overleftarrow{\gamma }\gamma (\eta \vee (\nu \cap \lambda ))\\ & =& \overleftarrow{\gamma }\gamma ((\eta \vee \nu )\cap (\eta \vee \lambda ))\\ & =& \overleftarrow{\gamma }\gamma (\eta \vee \nu )\cap \overleftarrow{\gamma }\gamma (\eta \vee \lambda )\\ & =& (\eta \underset{―}{\vee }\nu )\cap (\eta \underset{―}{\vee }\lambda )\end{array}$

Thus $F{F}_{\gamma }(L)$ is a distributive lattice. Next we prove the completeness. Since $(1{)}^{+}$ and L are γ-filters, ${\chi }_{(1{)}^{+}}$ and χ_L are least and greatest elements of $F{F}_{\gamma }(L)$ respectively. Let $\{{\nu }_i:i\in I\}\subseteq F{I}_{\gamma }(L)$. Then $\bigcap _{i\in I}{\nu }_i$ is a fuzzy filter of L and $\bigcap _{i\in I}{\nu }_i\subseteq \overleftarrow{\gamma }\gamma (\bigcap _{i\in I}{\nu }_i)$.

$\begin{array}{lll}\bigcap _{i\in I}{\nu }_i\subseteq {\nu }_i,\mathrm{\forall }i\in I& \Rightarrow & \overleftarrow{\gamma }\gamma (\bigcap _{i\in I}{\nu }_i)\subseteq {\nu }_i,\mathrm{\forall }i\in I\\ & \Rightarrow & \overleftarrow{\gamma }\gamma (\bigcap _{i\in I}{\nu }_i)\subseteq \bigcap _{i\in I}{\nu }_i\end{array}$

Thus $\overleftarrow{\gamma }\gamma (\bigcap _{i\in I}{\nu }_i)=\bigcap _{i\in I}{\nu }_i$. So $F{F}_{\gamma }(L),\wedge ,\underset{―}{\vee })$ is a complete distributive lattice.

Theorem 3.18.

The set $F{F}_{\gamma }(L)$ is isomorphic to the lattice of fuzzy ideals of $B_{\ast }(L)$.

Proof.

Define

$\begin{array}{l}f:F{F}_{\gamma }(L)⟶FI(B_{\ast }(L)),f(\nu )=\gamma (\nu ),\mathrm{\forall }\eta \in F{F}_{\gamma }(L).\end{array}$

Let $\eta ,\nu \in F{F}_{\gamma }(L)$ and $f(\eta )=f(\nu )$. Then $\gamma (\eta )=\gamma (\nu )$. Thus $\overleftarrow{\gamma }\gamma (\eta )=\overleftarrow{\gamma }\gamma (\nu )$. So $\eta =\nu$. Hence f is one to one.

Let $\lambda \in FI(B_{\ast }(L))$. Then by Lemma 3.2, $\overleftarrow{\gamma }(\lambda )$ is a fuzzy filter of L. Now we proceed to show that $\overleftarrow{\gamma }(\lambda )$ is a $\gamma -\text{fuzzy}$ filter of L. Let $x\in L$. Then $\overleftarrow{\gamma }\gamma (\overleftarrow{\gamma }(\lambda ))(x)=\gamma \overleftarrow{\gamma }(\lambda )((x{)}^{+})$. Thus by Lemma 3.8, we get that $\gamma \overleftarrow{\gamma }(\lambda )((x{)}^{+})=\overleftarrow{\gamma }(\eta )(x)$. So $\overleftarrow{\gamma }(\lambda )=\overleftarrow{\gamma }\gamma (\overleftarrow{\gamma }(\lambda ))$. Thus for each $\lambda \in FI(B_{\ast }(L)),f(\overleftarrow{\gamma }(\lambda ))=\lambda$. Therefore, f is onto.

Now for any $\eta ,\theta \in F{I}_{\gamma }(L)$, $f(\eta \underset{―}{\vee }\theta )=f(\overleftarrow{\gamma }\gamma (\eta \vee \theta ))=\gamma (\overleftarrow{\gamma }\gamma (\eta \vee \theta ))=\gamma (\eta \vee \theta )=\gamma (\eta )\vee \gamma (\theta )=f(\eta )\vee f(\theta )$. Similarly $f(\eta \cap \theta )=f(\eta )\cap f(\theta )$. Therefore, f is an isomorphism of $F{F}_{\gamma }(L)$ onto the lattice of fuzzy filters of $B_{\ast }(L)$

Theorem 3.19.

The following are equivalent for each non-constant $\gamma -\text{fuzzy}$ filter λ of L.

(1)	For all $\theta ,\eta \in FF(L)$, $\begin{array}{l}\theta \cap \eta \subseteq \lambda \Rightarrow \theta \subseteq \lambda \mathrm{or}\eta \subseteq \lambda .\end{array}$
(2)	For any fuzzy points xα and yβ of L, $\begin{array}{l}{x}_{\alpha }+y_{\beta }\subseteq \lambda \Rightarrow x_{\alpha }\subseteq \lambda \mathrm{or}{y}_{\beta }\subseteq \lambda .\end{array}$
(3)	For all $\theta ,\eta \in F{I}_{\gamma }(L)$, $\begin{array}{l}\theta \cap \eta \subseteq \lambda \Rightarrow \theta \subseteq \lambda \mathrm{or}\eta \subseteq \lambda .\end{array}$

Proof.

$1\Rightarrow 2$: Let $x,y\in L$ such that $x_{\alpha }+y_{\beta }\subseteq \lambda$. Then $[x_{\alpha }+y_{\beta })\subseteq \lambda$. Since L is a distributive lattice, by Lemma 3.3 of (Norahun & Zeleke, 2021), we have $[x_{\alpha })\cap [y_{\beta })\subseteq \lambda$. Since $[x_{\alpha })$ and $[y_{\beta })$ are fuzzy filters of L, by the assumption, $[x_{\alpha })\subseteq \lambda$ or $[y_{\beta })\subseteq \lambda$. This shows that $x_{\alpha }\subseteq \lambda$ or $y_{\beta }\subseteq \lambda$.

$2\Rightarrow 3$: Let $\theta ,\eta \in F{I}_{\gamma }(L)$ such that $\theta \cap \eta \subseteq \lambda$. Now we need to show $\theta \subseteq \lambda$ or $\eta \subseteq \lambda$. Suppose not. Then $\theta ⊈\lambda$ and $\eta ⊈\lambda$. Which implies there exist $x,y\in L$ such that $\theta (x)>\lambda (x)$ and $\eta (y)>\lambda (y)$. Put $\theta (x)=\alpha$ and $\eta (y)=\beta$. Then $x_{\alpha }⊈\lambda$ and $y_{\beta }⊈\lambda$. Since $x_{\alpha }+y_{\beta }\subseteq \theta \cap \eta$, we have $x_{\alpha }+y_{\beta }\subseteq \lambda$. By the assumption, we get that $x_{\alpha }\subseteq \lambda$ or $y_{\beta }\subseteq \lambda$. Which is a contradiction. Thus $\theta \subseteq \lambda$ or $\eta \subseteq \lambda$.

$3\Rightarrow 1$: Suppose $\theta ,\eta \in FF(L)$ such that $\theta \cap \eta \subseteq \lambda$. Then by Corollary 3.7 we have $\overleftarrow{\gamma }\gamma (\theta )\cap \overleftarrow{\gamma }\gamma (\eta )\subseteq \lambda$. Since $\overleftarrow{\gamma }\gamma (\theta )$ and $\overleftarrow{\gamma }\gamma (\eta )$ are $\gamma -\text{fuzzy}$ filters, by the assumption, we get that $\overleftarrow{\gamma }\gamma (\theta )\subseteq \lambda$ or $\overleftarrow{\gamma }\gamma (\eta )\subseteq \lambda$. Which implies $\theta \subseteq \lambda$ or $\eta \subseteq \lambda$.

Definition 3.20.

By a prime $\gamma -\text{fuzzy}$ filter, we mean a non-constant $\gamma -\text{fuzzy}$ filter of L satisfying (1) and hence all of the condition of Theorem 3.19.

We have proved in Theorem 3.18 that, there is an order isomorphism between the class of $\gamma -\text{fuzzy}$ filters and the set of fuzzy ideals of $B_{\ast }(L)$. Now, we show that there is an isomorphism between the prime $\gamma -\text{fuzzy}$ filters and the prime fuzzy ideals of the lattice of boosters of L.

Theorem 3.21.

There is an isomorphism between the prime $\gamma -\text{fuzzy}$ filters and the prime fuzzy ideals of the lattice of booster.

Proof.

By Theorem 3.18 the map f is an isomorphism from $F{F}_{\gamma }(L)$ into $FI(B_{\ast }(L))$. Let σ be a prime $\gamma -\text{fuzzy}$ filter of L. Then $\gamma (\sigma )\in FI(B_{\ast }(L))$. Now we prove $\gamma (\sigma )$ is a prime fuzzy ideal of $FI(B_{\ast }(L))$. Let $\theta ,\eta \in FI(B_{\ast }(L))$ such that $\theta \cap \eta \subseteq \gamma (\sigma )$. Since f is onto, there exist $\lambda ,\mu \in F{F}_{\gamma }(L)$ such that $f(\lambda )=\theta$ and $f(\mu )=\eta$. Thus $\gamma (\lambda \cap \mu )\subseteq \gamma (\sigma )$. Since $\overleftarrow{\gamma }$ is an isotone, we have $\overleftarrow{\gamma }\gamma (\lambda \cap \mu )\subseteq \overleftarrow{\gamma }\gamma (\sigma )$. Thus $\lambda \cap \mu \subseteq \sigma$. Since σ is a prime fuzzy filter, either $\lambda \subseteq \sigma$ or $\mu \subseteq \sigma$. This shows that either $\gamma (\lambda )\subseteq \gamma (\sigma )$ or $\gamma (\mu )\subseteq \gamma (\sigma )$. Thus $\theta \subseteq \gamma (\sigma )$ or $\eta \subseteq \gamma (\sigma )$. Hence $\gamma (\sigma )$ is a prime fuzzy ideal of $B_{\ast }(L)$.

Conversely, suppose that θ is a prime fuzzy ideal in $B_{\ast }(L)$. Since f is onto, there exists a $\gamma -\text{fuzzy}$ filter σ in $F{F}_{\gamma }(L)$ such that $\theta =\gamma (\sigma )$. Let $\eta ,\lambda \in FF(L)$ such that $\eta \cap \lambda \subseteq \sigma$. Since γ is an isotone, we get $\gamma (\eta \cap \lambda )\subseteq \gamma (\sigma )=\theta$. Thus $\gamma (\eta )\cap \gamma (\lambda )\subseteq \gamma (\sigma )$. Since $\gamma (\sigma )$ is a prime fuzzy ideal of $B_{\ast }(L)$, either $\gamma (\eta )\subseteq \gamma (\sigma )$ or $\gamma (\lambda )\subseteq \gamma (\sigma )$. This implies $\eta \subseteq \overleftarrow{\gamma }\gamma (\sigma )$ or $\lambda \subseteq \overleftarrow{\gamma }\gamma (\sigma )$. Since σ is a $\gamma -\text{fuzzy}$ filter, we get $\eta \subseteq \sigma$ or $\lambda \subseteq \sigma$. Thus σ is prime fuzzy filter in $F{F}_{\gamma }(L)$. So the prime $\gamma -\text{fuzzy}$ filters corresponds to prime fuzzy ideals of $B_{\ast }(L)$.

Theorem 3.22.

Let θ be a $\gamma -\text{fuzzy}$ filter of L and η be a fuzzy ideal of L such that $\theta \cap \eta \le \alpha$, $\alpha \in [0,1)$. Then there exists a prime $\gamma -\text{fuzzy}$ filter λ of L such that $\theta \subseteq \lambda$ and $\lambda \cap \eta \le \alpha$.

Proof.

Put $\mathcal{P}=\{\sigma \in F{F}_{\gamma }(L):\sigma \subseteq \eta \mathtt{\text{and}}\eta \cap \sigma \le \alpha \}$. Since $\theta \in \mathcal{P}$, $\mathcal{P}$ is nonempty and it forms a poset together with the inclusion ordering of fuzzy sets. Let $\mathcal{A}=\{{\theta }_i{\}}_{i\in I}$ be any chain in $\mathcal{P}$. Then clearly $\bigcup _{i\in I}{\theta }_i$ is a $\gamma -\text{fuzzy}$ filter. Since ${\theta }_i\cap \eta \le \alpha$ for each $i\in I$, we get that $(\bigcup _{i\in I}{\theta }_i)\cap \eta \le \alpha$. Thus $\bigcup _{i\in I}{\theta }_i\in \mathcal{A}$. By applying Zorn’s lemma we get a maximal element, let say $\sigma \in \mathcal{P}$; that is σ is a $\gamma -\text{fuzzy}$ filter of L such that $\theta \subseteq \sigma$ and $\sigma \cap \eta \le \alpha$.

Now we proceed to show σ is a prime fuzzy filter. Assume that σ is not prime fuzzy filter. Let ${\mu }_1\cap {\mu }_2\subseteq \theta$ such that ${\mu }_1⊈\theta$ and ${\mu }_2⊈\theta ,{\mu }_1,{\mu }_2\in FF(L)$. If we put ${\sigma }_1=\overleftarrow{\gamma }\gamma ({\mu }_1\vee \sigma )$ and ${\sigma }_2=\overleftarrow{\gamma }\gamma ({\mu }_2\vee \sigma )$, then both σ₁ and σ₂ are $\gamma -\text{fuzzy}$ filters of L properly containing σ. Since σ is maximal in $\mathcal{P}$, we get ${\sigma }_1,{\sigma }_2\notin \mathcal{P}$. Thus ${\sigma }_1\cap \eta \nleqq \alpha$ and ${\sigma }_2\cap \eta \nleqq \alpha$. This implies there exist $x,y\in L$ such that $({\sigma }_1\cap \eta )(x)>\alpha$ and $({\sigma }_2\cap \eta )(y)>\alpha$. Which implies $(({\sigma }_1\cap {\sigma }_2)\cap \eta )(x\wedge y)>\alpha \Rightarrow (\overleftarrow{\gamma }\gamma (\sigma \vee ({\mu }_1\wedge {\mu }_2))(x\wedge y)\wedge \eta (x\wedge y)>\alpha$. This shows that $(\theta \cap \eta )(x\wedge y)>\alpha$. This is a contradiction. Thus σ is prime $\gamma -\text{fuzzy}$ filter of L.

Corollary 3.23.

Let θ be a $\gamma -\text{fuzzy}$ filter of L, $a\in L$ and $\alpha \in [0,1)$. If $\theta (a)\le \alpha$, then there exists a prime $\gamma -\text{fuzzy}$ filter η of L such that $\theta \subseteq \eta$ and $\eta (a)\le \alpha$.

Proof.

Put $\mathcal{P}=\{\sigma \in F{F}_{\gamma }(L):\theta \subseteq \sigma \mathtt{\text{and}}\sigma (a)\le \alpha \}$. Since $\theta \in \mathcal{P}$, $\mathcal{P}$ is nonempty and it forms a poset together with the inclusion ordering of fuzzy sets. Let $\mathcal{A}=\{{\theta }_i{\}}_{i\in I}$ be any chain in $\mathcal{P}$. Clearly $\bigcup _{i\in I}{\theta }_i$ is a $\gamma -\text{fuzzy}$ filter. Since ${\theta }_i(a)\le \alpha$ for each $i\in I$, α is an upper bound of $\{{\theta }_i(a):i\in I\}$. Thus $\bigcup _{i\in I}{\theta }_i(a)\le \alpha$. So $\bigcup _{i\in I}{\theta }_i$ is a $\gamma -\text{fuzzy}$ filter containing θ and $\bigcup _{i\in I}{\theta }_i(a)\le \alpha$. Hence $\bigcup _{i\in I}{\theta }_i\in \mathcal{P}$. By applying Zorn’s lemma we get a maximal element, let say $\sigma \in \mathcal{P}$; that is σ is a $\gamma -\text{fuzzy}$ filter of L such that $\theta \subseteq \sigma$ and $\sigma (a)\le \alpha$.

Now we proceed to show σ is a prime fuzzy filter. Assume that σ is not prime fuzzy filter. Let ${\mu }_1\cap {\mu }_2\subseteq \sigma$ and ${\mu }_1⊈\sigma$ and ${\mu }_2⊈\sigma ,{\mu }_1,{\mu }_2\in FF(L)$. If we put ${\sigma }_1=\overleftarrow{\gamma }\gamma ({\mu }_1\vee \sigma )$ and ${\sigma }_2=\overleftarrow{\gamma }\gamma ({\mu }_2\vee \sigma )$, then both σ₁ and σ₂ are $\gamma -\text{fuzzy}$ filters of L properly containing σ. Since σ is maximal in $\mathcal{P}$, we get ${\sigma }_1,{\sigma }_2\notin \mathcal{P}$. Thus ${\sigma }_1(a)>\alpha$ and ${\sigma }_2(a)>\alpha$. Now $$\begin{gathered} (sigm{a}_1\cap {\sigma }_2)(a)=\overleftarrow{\gamma }\gamma (({\mu }_1\vee \sigma )\cap ({\mu }_2\vee \sigma )) \\ (a)=\overleftarrow{\gamma }\gamma (({\mu }_1\cap {\mu }_2)\vee \sigma ))(a)=\sigma (a)>\alpha \end{gathered}$$. This is a contradiction. Hence σ is prime $\gamma -\text{fuzzy}$ filter.

Corollary 3.24.

For any $\gamma -\text{fuzzy}$ filter of L is the intersection of all prime $\gamma -\text{fuzzy}$ filters containing it.

Proof.

Let θ be a proper $\gamma -\text{fuzzy}$ filter of L. Consider the following.

$\begin{array}{l}\lambda =\bigcap \{\eta :\eta \mathit{\text{is a prime}}\gamma -\text{fuzzy}\mathit{\text{filter and}}\theta \subseteq \eta \}.\end{array}$

Clearly $\theta \subseteq \lambda$. Assume that $\lambda ⊈\theta$. Then there is $a\in L$ such that $\lambda (a)>\theta (a)$. Let $\theta (a)=\alpha$. Consider the set

$\begin{array}{l}\mathcal{P}=\{\eta \in F{I}_{\gamma }(L):\theta \subseteq \eta \mathtt{\text{and}}\eta (a)\le \alpha \}.\end{array}$

By the above corollary we can find a prime $\gamma -\text{fuzzy}$ filter µ of L such that $\theta \subseteq \mu$ and $\mu (a)\le \alpha$. This implies $\lambda \subseteq \mu$. This shows that $\lambda (a)\le \alpha$. Which is a contradiction. Thus $\lambda \subseteq \theta$. So $\lambda =\theta$.

4. The space of prime γ-fuzzy filters

In this section, we study the space of prime $\gamma -\text{fuzzy}$ filters of a pseudo-complemented distributive lattice and some properties of the space also studied.

Let ${\mathcal{P}}_{\gamma }$ be the set of all prime $\gamma -\text{fuzzy}$ filters of a pseudo-complemented distributive lattice. Let $\mathrm{\Gamma }(\lambda )=\{\nu \in {\mathcal{P}}_{\gamma }:\lambda \subseteq \nu \}$ where λ is a fuzzy subset of L and $\mathcal{P}(\lambda )=\{\nu \in {\mathcal{P}}_{\gamma }:\lambda ⊈\nu \}={\mathcal{P}}_{\gamma }-\mathrm{\Gamma }(\lambda )$. We let ${\gamma }_{\ast }={\gamma }_1$, i.e. ${\gamma }_{\ast }=\{x\in L:\gamma (x)=1\}$.

Lemma 4.1.

Let η and ν be fuzzy filters of L. Then

(1)	$\eta \subseteq \nu \Rightarrow \mathcal{P}(\eta )\subseteq \mathcal{P}(\nu )$
(2)	$\mathcal{P}(\eta \vee \nu )=\mathcal{P}(\eta )\cup \mathcal{P}(\nu )$
(3)	$\mathcal{P}(\eta \cap \nu )=\mathcal{P}(\eta )\cap \mathcal{P}(\nu )$

Proof.

1. Let $\eta \subseteq \nu$ and $\delta \in \mathcal{P}(\eta )$. Then $\eta ⊈\delta$ and $\nu ⊈\delta$. Thus $\delta \in \mathcal{P}(\nu )$.

2. By (1), we have $\mathcal{P}(\eta )\cup \mathcal{P}(\nu )\subseteq \mathcal{P}(\eta \vee \nu )$. To show the other inclusion, let $\delta \in \mathcal{P}(\eta \vee \nu )$. Then $\eta \vee \nu ⊈\delta$. Thus either $\eta ⊈\delta$ or $\nu ⊈\delta$. So $\delta \in \mathcal{P}(\eta )\cup \mathcal{P}(\nu )$. Hence $\mathcal{P}(\eta \vee \nu )=\mathcal{P}(\eta )\cup \mathcal{P}(\nu )$.

3. It can be easily verified that $\mathcal{P}(\eta \cap \nu )\subseteq \mathcal{P}(\eta )\cap \mathcal{P}(\nu )$. To show the other inclusion, let $\delta \in \mathcal{P}(\eta )\cap \mathcal{P}(\nu )$. Then $\eta ⊈\delta \mathtt{\text{and}}\nu ⊈\delta$. Since δ is a prime fuzzy filter, we have $\eta \cap \nu ⊈\delta$. Thus $\delta \in \mathcal{P}(\eta \cap \nu )$. So $\mathcal{P}(\eta \cap \nu )=\mathcal{P}(\eta )\cap \mathcal{P}(\nu )$.

Lemma 4.2.

Let λ be a fuzzy subset of L. Then $\mathcal{P}(\lambda )=\mathcal{P}([\lambda ))$.

Proof.

Since $\lambda \subseteq [\lambda )$, we have $\mathcal{P}(\lambda )\subseteq \mathcal{P}([\lambda ))$. Let $\delta \in \mathcal{P}([\lambda ))$. Then $[\lambda )⊈\delta$. We need to show $\lambda ⊈\delta$. Assume that $\lambda \subseteq \delta$. Then $[\lambda )\subseteq \delta$. Which is a contradiction. Thus $\lambda ⊈\delta$. So $\mathcal{P}(\lambda )=\mathcal{P}([\lambda ))$.

Theorem 4.3.

Let $a,b\in L$ and $\alpha \in (0,1]$. Then

1.	$\mathcal{P}((a\wedge b{)}_{\alpha })=\mathcal{P}(a_{\alpha })\cup \mathcal{P}(b_{\alpha })$
2.	$\mathcal{P}((a\vee b{)}_{\alpha })=\mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })$
3.	$\bigcup _{a\in L,\alpha \in (0,1]}\mathcal{P}(a_{\alpha })={\mathcal{P}}_{\gamma }$.

Proof.

(1) If $\nu \in \mathcal{P}(a_{\alpha })\cup \mathcal{P}(b_{\alpha })$, then either $a_{\alpha }⊈\nu$ or $b_{\alpha }⊈\nu$. Which implies either $\alpha >\nu (a)$ or $\alpha >\nu (b)$. This shows that $\alpha >\nu (a)\wedge \nu (b)=\nu (x\wedge y)$. Thus $(a\wedge b{)}_{\alpha }⊈\nu$. Hence $\nu \in \mathcal{P}((a\wedge b{)}_{\alpha })$. To show the other inclusion, let $\nu \in \mathcal{P}(a\wedge b{)}_{\alpha }$. Then $\alpha >\nu (a\wedge b)=\nu (a)\wedge \nu (b)$. This implies either $a_{\alpha }⊈\nu$ or $b_{\alpha }⊈\nu$. Thus $\nu \in \mathcal{P}(a_{\alpha })\cup \mathcal{P}(b_{\alpha })$.

(2) If $\nu \in \mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })$, then $a_{\alpha }⊈\nu$ and $b_{\alpha }⊈\nu$. This implies $\alpha >\nu (a)$ and $\alpha >\nu (b)$. This shows that $a,b\notin {\nu }_{\ast }$. Since ν is prime fuzzy filter, card Im ν = 2 and ${\nu }_{\ast }$ is prime. Thus $a\vee b\notin {\nu }_{\ast }$. Which implies $\alpha >\nu (a\vee b)$. Thus $(a\vee b{)}_{\alpha }⊈\nu$ and hence $\mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })\subseteq \mathcal{P}((a\wedge b{)}_{\alpha })$.

Conversely, let $\nu \in \mathcal{P}((a\vee b{)}_{\alpha })$. Then $(a\vee b{)}_{\alpha }⊈\nu$. Which implies $\alpha >\nu (a\vee b)\ge \nu (a)\vee \nu (b)$. Thus $\alpha >\nu (a)$ and $\alpha >\nu (b)$. This shows that $a_{\alpha }⊈\nu$ and $b_{\alpha }⊈\nu$. Thus $\nu \in \mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })$. So $\mathcal{P}((a\vee b{)}_{\alpha })\subseteq \mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })$. Therefore, $\mathcal{P}((a\vee b{)}_{\alpha })=\mathcal{P}(a_{\alpha })\cap \mathcal{P}(b_{\alpha })$.

(3) To show ${\mathcal{P}}_{\gamma }\subseteq \bigcup _{a\in L,\alpha \in (0,1]}\mathcal{P}(a_{\alpha })$, let $\nu \in {\mathcal{P}}_{\gamma }$. Since ν is prime fuzzy filter, ν is two valued. Thus $Im\nu =\{1,\beta \},\beta \in [0,1)$. This implies that there is $a\in L$ such that $\nu (a)=\beta$. Let us take some $\alpha \in (0,1]$ such that $\alpha >\beta$. Then $a_{\alpha }(a)=\alpha$. Which implies that $a_{\alpha }(a)>\nu (a)$. Thus $a_{\alpha }⊈\nu$ and hence ${\mathcal{P}}_{\gamma }\subseteq \bigcup _{a\in L,\alpha \in (0,1]}\mathcal{P}(a_{\alpha })$. Therefore, ${\mathcal{P}}_{\gamma }=\bigcup _{a\in L,\alpha \in (0,1]}\mathcal{P}(a_{\alpha })$.

Lemma 4.4.

Let ${\alpha }_1,{\alpha }_1\in (0,1]$; $\alpha =min\{{\alpha }_1,{\alpha }_2\}$ and $a,b\in L$. Then

$\begin{array}{l}\mathcal{P}(a_{{\alpha }_1})\cap \mathcal{P}(b_{{\alpha }_2})=\mathcal{P}((a\vee b{)}_{\alpha }).\end{array}$

Proof.

If $\nu \in \mathcal{P}(a_{{\alpha }_1})\cap \mathcal{P}(b_{{\alpha }_2})$, then $a_{{\alpha }_1}⊈\nu$ and $a_{{\alpha }_2}⊈\nu$. This implies that ${\alpha }_1>\nu (x)$ and ${\alpha }_2>\nu (y)$. Since ${\nu }_{\ast }$ is prime filter and $a,b\notin {\nu }_{\ast }$, we have $a\vee b\notin {\nu }_{\ast }$ and $\nu (a)=\nu (b)=\nu (a\vee b)$. This shows that $\alpha >\nu (a\vee b)$. Thus $(a\vee b{)}_{\alpha }⊈\nu$ and hence $\nu \in \mathcal{P}((a\vee b{)}_{\alpha })$. To show the other inclusion, let $\nu \in \mathcal{P}((a\vee b{)}_{\alpha })$. Then $\alpha >\nu (a\vee b)\ge \nu (a)\vee \nu (b)$. This implies ${\alpha }_1>\nu (a)$ and ${\alpha }_2>\nu (b)$. Thus $a_{{\alpha }_1}⊈\nu$ and $b_{{\alpha }_2}⊈\nu$. So $\nu \in \mathcal{P}(a_{{\alpha }_1})\cap \mathcal{P}(b_{{\alpha }_2})$. Hence $\mathcal{P}(a_{{\alpha }_1})\cap \mathcal{P}(b_{{\alpha }_2})=\mathcal{P}((a\vee b{)}_{\alpha })$.

Lemma 4.5.

Let $\{{\lambda }_i:i\in I\}$ be any family of fuzzy filters of L. Then

$\bigcap _{i\in I}\mathrm{\Gamma }({\lambda }_i)=\mathrm{\Gamma }([\bigcup _{i\in I}{\lambda }_i)).$

Proof.

Since ${\lambda }_i\subseteq [\bigcup _{i\in I}{\lambda }_i)$ for each $i\in I$, we have $\mathrm{\Gamma }([\bigcup _{i\in I}{\lambda }_i))\subseteq \mathrm{\Gamma }({\lambda }_i)$ for each $i\in I$. Thus $\mathrm{\Gamma }([\bigcup _{i\in I}{\lambda }_i))\subseteq \bigcap _{i\in I}\mathrm{\Gamma }({\lambda }_i)$.

Conversely, let $\lambda \in \bigcap _{i\in I}\mathrm{\Gamma }({\lambda }_i)$. Then $\lambda \in \mathrm{\Gamma }({\lambda }_i)$ for each $i\in I$. This implies ${\lambda }_i\subseteq \lambda$. Thus for any $a\in L$, $\lambda (a)$ is an upper bound of $\{{\lambda }_i(a):i\in I\}$. This implies that $Sup\{{\lambda }_i(a):i\in I\}\le \lambda (a)$. This shows that $\bigcup _{i\in I}{\lambda }_i\subseteq \lambda$ and $[\bigcup _{i\in I}{\lambda }_i)\subseteq \lambda$. So $\lambda \in \mathrm{\Gamma }([\bigcup _{i\in I}{\theta }_i))$. Thus $\bigcap _{i\in I}\mathrm{\Gamma }({\lambda }_i)\subseteq \mathrm{\Gamma }((\bigcup _{i\in I}{\lambda }_i])$. Hence $\bigcap _{i\in I}V({\lambda }_i)=\mathrm{\Gamma }([\bigcup _{i\in I}{\lambda }_i))$.

Theorem 4.6.

The collection $$\begin{gathered} \mathcal{T}=\{\mathcal{P}(\nu ):\nu \mathit{\text{is a fuzzy}} \\ \mathit{\text{filter of L}}\}\mathit{\text{is a topology on}}{\mathcal{P}}_{\gamma } \end{gathered}$$.

Proof.

Consider the fuzzy subsets ${\nu }_1,{\nu }_2$ of L defined as: ${\nu }_1(a)=0$ and ${\nu }_2(a)=1$ for all $a\in L$. Clearly $[{\nu }_1)$ and ν₂ are fuzzy filters of L. Again, $[{\nu }_1)\subseteq \lambda$, for all $\lambda \in {\mathcal{P}}_{\gamma }$. Then $\mathrm{\Gamma }([{\nu }_1))={\mathcal{P}}_{\gamma }$ and thus $\mathcal{P}({\nu }_1)=\varphi$. Since each $\lambda \in {\mathcal{P}}_{\gamma }$ is non-constant, ${\nu }_2⊈\lambda$ for all $\lambda \in {\mathcal{P}}_{\gamma }$. So $\mathcal{P}({\nu }_2)={\mathcal{P}}_{\gamma }$. Hence $\varphi ,{\mathcal{P}}_{\gamma }\in \mathcal{T}$.

Next, let $\mathcal{P}({\nu }_1),\mathcal{P}({\nu }_2)\in \mathcal{T}$. Since ν₁ and ν₂ are fuzzy filters of L, then by Lemma 4.1, we get that $\mathcal{P}({\nu }_1)\cap \mathcal{P}({\nu }_2)=\mathcal{P}({\nu }_1\cap {\nu }_2)$. Then $\mathcal{T}$ is closed under finite intersection.

Finally, let $\{{\nu }_i:i\in I\}$ be any family of fuzzy filters of L. Then by Lemma 4.5 we have

$\begin{array}{l}\bigcap _{i\in I}\mathrm{\Gamma }({\nu }_i)=\mathrm{\Gamma }([\bigcup _{i\in I}{\nu }_i)).\end{array}$

Which implies $\bigcup _{i\in I}\mathcal{P}({\nu }_i)=\mathcal{P}([\bigcup _{i\in I}{\nu }_i))$. Thus by Lemma 4.2, we get that

$X(\bigcup _{i\in I}{\nu }_i)=\mathcal{P}([\bigcup _{i\in I}{\nu }_i)).$

So $\mathcal{T}$ is closed under arbitrary union. Consequently, $\mathcal{T}$ is a topology on ${\mathcal{P}}_{\gamma }$. The space $({\mathcal{P}}_{\gamma },\mathcal{T})$ will be called the space of prime $\gamma -\text{fuzzy}$ filters in L.

In the above theorem we proved that, the family of $\mathcal{P}(\lambda )$ is a topology on ${\mathcal{P}}_{\gamma }$. In the following result, we show that the set of all open sets of the form $\mathcal{P}(x_{\alpha })$ is a basis for the topology on ${\mathcal{P}}_{\gamma }$.

Theorem 4.7.

The collection $\mathcal{B}=\{\mathcal{P}(a_{\alpha }):a\in L,\alpha \in (0,1]\}$ forms base for some topology ${\mathcal{P}}_{\gamma }$.

Proof.

Let $\mathcal{P}(\nu )$ be any open set in ${\mathcal{P}}_{\gamma }$ and $\lambda \in \mathcal{P}(\nu )$. Then $\nu ⊈\lambda$ and there is $a\in L$ such that $\nu (a)>\lambda (a)$. Put $\nu (a)=\alpha$, then $a_{\alpha }\subseteq \nu$ and $\lambda \in \mathcal{P}(a_{\alpha })$. To show $\mathcal{P}(a_{\alpha })\subseteq \mathcal{P}(\nu )$, let $\eta \in \mathcal{P}(a_{\alpha })$. Then $a_{\alpha }⊈\eta$ and $\nu (a)>\eta (a)$. Which implies $\eta \in \mathcal{P}(\nu )$. Thus $\lambda \in \mathcal{P}(a_{\beta })\subseteq \mathcal{P}(\nu )$. Hence for any open set $\mathcal{P}(\nu )$ in ${\mathcal{P}}_{\gamma }$ we can find $\mathcal{P}(a_{\alpha })$ in $\mathcal{B}$ such that $\mathcal{P}(a_{\alpha })\subseteq \mathcal{P}(\nu )$. Therefore, $\mathcal{B}$ is a base for $\mathcal{T}$.

Theorem 4.8.

The space ${\mathcal{P}}_{\gamma }$ is a T₀-space.

Proof.

Let $\nu ,\lambda \in {\mathcal{P}}_{\gamma }$ such that $\nu \ne \lambda$. Then either $\nu ⊈\lambda$ or $\lambda ⊈\nu$. Without loss of generality, we can assume that $\nu ⊈\lambda$. Then $\lambda \in \mathcal{P}(\nu )$ and $\nu \notin \mathcal{P}(\nu )$. Thus ${\mathcal{P}}_{\gamma }$ is a T₀-space.

Theorem 4.9.

For any fuzzy filter λ of L, $\mathcal{P}(\lambda )=\mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda ))$.

Proof.

For any fuzzy filter λ of L, we have $\lambda \subseteq \overleftarrow{\gamma }\gamma (\lambda )$ and $\mathcal{P}(\lambda )\subseteq \mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda ))$. Let $\nu \in \mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda ))$. Then $\overleftarrow{\gamma }\gamma (\lambda ))⊈\nu$. Suppose $\nu \notin \mathcal{P}(\lambda )$, then $\lambda \subseteq \nu$. This implies $\overleftarrow{\gamma }\gamma (\lambda )\subseteq \overleftarrow{\gamma }\gamma (\nu ))=\nu$. Which is impossible. Thus $\nu \in \mathcal{P}(\lambda )$ and hence $\mathcal{P}(\lambda )=\mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda ))$.

In the following result, we show that there is a one to one correspondence between the class of $\gamma -\text{fuzzy}$ filters and the lattice of all open sets in ${\mathcal{P}}_{\gamma }$.

Theorem 4.10.

The lattice $F{F}_{\gamma }(L)$ is isomorphic with the lattice of all open sets in ${\mathcal{P}}_{\gamma }$.

Proof.

The lattice of all open sets in X_γ is $(\mathcal{T},\cap ,\cup )$. Define the mapping

$\begin{array}{l}f:F{F}_{\gamma }(L)⟶\mathcal{T}\mathrm{by}f(\lambda )=\mathcal{P}(\lambda )\mathrm{for}\mathrm{all}\lambda \in {\mathcal{P}}_{\gamma }.\end{array}$

Since $\mathcal{P}(\lambda )=\mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda ))$ and $\overleftarrow{\gamma }\gamma (\lambda )$ is a $\gamma -\text{fuzzy}$ filter, every open subset of ${\mathcal{P}}_{\gamma }$ is of the form $\mathcal{P}(\theta )$ for some $\theta \in F{F}_{\gamma }(L)$. Hence the map is onto.

Let $f(\lambda )=f(\theta )$. If $\lambda \ne \theta$, then there is $x\in L$ such that either $\lambda (x)<\theta (x)$ or $\theta (x)<\lambda (x)$. Without loss of generality, we can assume that $\lambda (x)<\theta (x)$. Put $\lambda (x)=\beta$. Then by Corollary 3.23, we can find a prime $\gamma -\text{fuzzy}$ filter η such that $\lambda \subseteq \eta$ and $\eta (x)\le \beta$. Thus $\eta \notin \mathcal{P}(\lambda )$ and $\theta ⊈\eta$. So $\eta \notin \mathcal{P}(\lambda )$ and $\eta \in \mathcal{P}(\theta )$. This is a contradiction. Hence $\lambda =\theta$.

Now we show that f is homomorphism. Let $\lambda ,\theta \in F{I}_{\gamma }(L)$. Then $f(\lambda \underset{―}{\vee }\theta )=\mathcal{P}(\overleftarrow{\gamma }\gamma (\lambda \vee \theta ))=\mathcal{P}(\lambda \vee \theta )=f(\lambda )\cup f(\theta )$. Similarly, $f(\lambda \cap \theta )=f(\lambda )\cap f(\theta )$. This shows that f is a homomorphism. Hence f is an isomorphism.

For any fuzzy subset λ of L, $\mathcal{P}(\lambda )=\{\nu \in {\mathcal{P}}_{\gamma }:\lambda ⊈\nu \}$ is an open set of ${\mathcal{P}}_{\gamma }$ and $\mathrm{\Gamma }(\lambda )=\{\nu \in {\mathcal{P}}_{\gamma }:\lambda \subseteq \nu \}={\mathcal{P}}_{\gamma }-\mathrm{\Gamma }(\theta )$ is a closed set of ${\mathcal{P}}_{\gamma }$. In the following result we prove the closure of a fuzzy set.

Theorem 4.11.

For any family $\mathcal{C}\subseteq {\mathcal{P}}_{\gamma }$, closure of $\mathcal{C}$ is given by $\bar{\mathcal{C}}=\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$.

Proof.

We know that closure of $\mathcal{C}$ is the smallest closed set containing $\mathcal{c}$. To prove our claim, it is enough to show that $\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$ is the smallest closed set containing $\mathcal{C}$. Since the set of all $\gamma -\text{fuzzy}$ filter is a complete distributive lattice, $\bigcap _{\nu \in \mathcal{C}}\nu$ is a $\gamma -\text{fuzzy}$ filter and $\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$ is a closed set in ${\mathcal{P}}_{\gamma }$. If $\delta \in \mathcal{C}$, then $\bigcap _{\nu \in \mathcal{C}}\nu \subseteq \delta$. Thus $\delta \in \mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$. This implies that $\mathcal{C}\subseteq \mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$. Let $\mathrm{\Gamma }(\eta )$ be any closed set in ${\mathcal{P}}_{\gamma }$ containing $\mathcal{C}$. Then $\eta \subseteq \nu$, for each $\nu \in \mathcal{C}$. Thus $\eta \subseteq \bigcap _{\nu \in \mathcal{C}}\nu$ and $\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )\subseteq \mathrm{\Gamma }(\eta )$. So $\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$ is the smallest closed set containing $\mathcal{C}$. Hence $\bar{\mathcal{C}}=\mathrm{\Gamma }(\bigcap _{\nu \in \mathcal{C}}\nu )$.

5. Conclusion

In this work, we studied the concept of $\gamma -\text{fuzzy}$ filters of a pseudo-complemented distributive lattice. We have shown that the set of all $\gamma -\text{fuzzy}$ filters of a distributive lattice forms a complete distributive lattice and isomorphic to the set of all fuzzy ideals of $B_{\ast }(L)$. We observed that every $\gamma -\text{fuzzy}$ filter is the intersection of all $\gamma -\text{fuzzy}$ filters containing it. We also studied the space of all prime $\gamma -\text{fuzzy}$ filters in a distributive lattice. Our future work will focus on σ-fuzzy ideals in a 0–1 distributive lattice.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

No data were used to support this study.