Analysis of fractional order model on the employees’ negative attitudes towards their workplace

ABSTRACT

In most countries throughout the world, the negative attitude of employees toward their workplace is a major concern through government as well as non-government institutions. The main objective of this study is to construct and analyze a novel employee negative attitude towards their workplace dissemination fractional order model and investigate the impacts of protection and improvement (rehabilitation) strategies. The qualitative analyses of the proposed model proved the model solutions non-negativity as well as boundedness, computed the model negative attitude-free, as well as negative attitude persistence equilibrium points, proved the local stability of equilibrium points, it also proved that the existence of backward bifurcation whenever the associated effective reproduction number is less unity. Numerical simulations have been carried out to verify the qualitative results and investigate the parameter effects and solutions behavior. Eventually, from the qualitative and numerical results, we observed and recommended that an optimal effort to implement the protection and improvement (rehabilitation) strategies simultaneously is the best possible strategy to reduce employees’ negative attitudes towards their workplace from the employees in the population under consideration.

KEYWORDS:

• employee
• negative attitude
• workplace
• fractional order model

1. Introduction

Attitude is a state of mind willingness organized with experience, exerting a dynamic influence on individual response to all situations it is related, and it can be either positive, negative, or neutral (Briñol et al., 2019; Saari & Judge, 2004). Employee attitude is everything, both within and without organizations or companies, for the growth and survival of an organization in today’s competitive environment of many organizations (Brayfield & Crockett, 1955; Ekhsan Abang Othman & Suleiman, 2013). In a workplace, the negative attitudes of employees harm the organization’s development which is why researchers suggest organizational research that applies positive psychology has to be focused on the fundamental organizational and individual factors that harm employee well-being at the workplace (Ekhsan Abang Othman & Suleiman, 2013; Tian et al., 2022; Williams et al., 2017). In the history of social psychology, the attitude has three fundamental components. These components are cognitive knowledge or beliefs that affect feelings or emotions and behavior like pre-disposition (Briñol et al., 2019; Saari & Judge, 2004).

Fractional order derivatives are naturally related to most dynamical systems and are crucial to studying the memory and hereditary properties, epidemiological properties, biological properties, and hereditary effects of any complex processes and materials that are neglected in classical integer-order models (Bedi et al., 2020, 2021; Kaushik et al., 2023; Panja, 2019c). Furthermore, it plays a fundamental role in controlling the chaotic nature of real-world dynamics situations in various disciplines (Dhaniya et al., 2023). Many researchers have investigated the significance of integer order derivatives in different fields, for instance, see the studies (Ketema Mamo, 2020; Panja, 2019b; Samuel Kotola et al., 2022; Tessema Alemneh & Yizengaw Alemu, 2021; Wondimagegnhu Teklu & Baye Terefe, 2022) and the fractional order derivatives in the field of mathematical biology, ecology, sociology, for instance, see the studies like (Barman et al., 2021; Mandal et al., 2020; Omame et al., 2022; Panja, 2019a; Wondimagegnhu Teklu, 2023, 2024, 2024; Wondimagegnhu Teklu et al., 2024). Therefore, mathematical models represented by the derivative of fractional order have been mostly used in different fields of research (Mandal et al., 2020). As discussed in paragraph one above different social sciences studies reveal the negative attitudes of employees towards their workplace but no one has studied the impacts of negative attitudes of employees towards their workplace using either integer order modeling or fractional order modeling approach. Having this in mind, we are motivated to formulate and analyze a fractional order model on employees’ negative attitudes towards their workplace. To gather information for constructing a fractional order model on employees’ negative attitudes towards their workplace we have reviewed relevant published literature such as (Wondimagegnhu Teklu, 2024) investigated the impacts of the proposed optimal control intervention strategies on the corruption dissemination in the community using fractional order derivatives. From the results of the numerical simulations, they recommended that implementing the three proposed time-dependent controlling strategies significantly minimizes corruption in the community. Wondimagegnhu Teklu & Baye Terefe (2022) formulated and examined a compartmental modeling approach to control the spreading of university students’ animosity towards mathematics with optimal control theory. Both the qualitative and numerical results show prevention and treatment control measures are the best strategies to minimize and possibly eradicate the animosity-infection in the university students’ community. Tessema Alemneh & Yizengaw Alemu (2021) investigated a mathematical model of social media addiction with optimal control strategies. The result suggested that educating the negative effects of social media, treating the addicted individuals and advertising are the best-integrated control strategies to fight against social media addiction. Wondimagegnhu Teklu (2023) constructed and analyzed a fractional order model on the dissemination dynamics of higher institution students’ anxiety towards mathematics with optimal control strategies. Belela and Teklu (Samuel Kotola et al., 2022) investigated the racism and corruption co-existence dissemination in the community using an integer order modeling approach. Barman et al. (2021) constructed a fractional-order prey-predator model to investigate the effects of predator-incited fear and prey refuge. Having the results of the above-reviewed literature above, we have formulated and analyzed novel employees’ negative attitudes towards their workplace factional order model (12). The study is organized as: section two discusses basic preliminaries important for the study, section three formulates the integer order model, section four re-formulated and analyzes the Caputo fractional order model, section five carries out the numerical simulations of the Caputo fractional-order model given in section four and conclusions are given in section six of the study.

2. Mathematical preliminaries

In this section, we recall some basic definitions of fractional calculus.

Definition 1.

(Carpinteri & Mainardi, 2014) The Caputo fractional order derivative with order θ for a function $\mathit{h}\in C^n$ is defined as

(1) $\begin{array}{ll}{}^c{D}_t^{\theta }\mathit{h}(\mathit{t})=& \frac{1}{\mathrm{\Gamma }(\mathit{n}-\mathit{\theta })}{\int }_0^t{h}^n(\mathit{\xi })\frac{(\mathit{t}-\mathit{\xi }{)}^{\mathit{n}-\mathit{\theta }}}{\mathit{t}-\mathit{\xi }}\mathit{d\xi },\\ & \mathit{n}-1<\mathit{\theta }\le \mathit{n}\in \mathit{N}.\end{array}$(1)

Note: ${}^c{D}_t^{\theta }\mathit{h}(\mathit{t})$ tends to h(t) as θ → 1.

Definition 2.

(Carpinteri & Mainardi, 2014) The Caputo fractional order integral with order θ > 0 for a function $\mathit{h}\in C^n$ is defined as

(2) ${}^C{I}_t^{\theta }\mathit{h}(\mathit{t})=\frac{1}{\mathrm{\Gamma }(\mathit{\theta })}{\int }_0^t\mathit{h}(\mathit{\xi })\frac{(\mathit{t}-\mathit{\xi }{)}^{\mathit{\theta }}}{\mathit{t}-\mathit{\xi }}\mathit{d\xi },0<\mathit{\theta }<1,\mathit{t}>0.$(2)

Definition 3.

(Atangana & Baleanu, 2016) The Atangana-Baleanu-Caputo (ABC) fractional operator of order $\mathit{\theta }\in [0,1]$ is defined as follows

(3) ${}_a^{ABC}{D}_t^{\theta }\mathit{h}(\mathit{t})=\frac{\mathit{ABC}(\mathit{\theta })}{1-\mathit{\theta }}{\int }_a^{\theta }\mathit{h}(\mathit{\xi })E_{\theta }[-\mathit{\theta }\frac{(\mathit{t}-\mathit{\xi }{)}^{\mathit{\theta }}}{\mathit{t}-\mathit{\theta }}]\mathit{d\xi },$(3)

where $E_{\theta }(.)$ is the Mittag-Leffler function, defined by,

(4) $E_{\theta }(t^{\mathit{\theta }})=\sum _{\mathit{k}=1}^{\mathrm{\infty }}\frac{t^{\mathit{\theta }}}{\mathrm{\Gamma }(\mathit{\theta K}+1)}.$(4)

Definition 4.

(Atangana & Baleanu, 2016) The associated ABC fractional integral of order θ is defined as follows

(5) $\begin{array}{ll}{}_a^{ABC}{I}_t^{\theta }\mathit{h}(\mathit{t})=& \frac{1-\mathit{\theta }}{\mathit{B}(\mathit{\theta })}\mathit{h}(\mathit{t})+\frac{\theta }{\mathit{B}(\mathit{\theta })\mathrm{\Gamma }(\mathit{\theta })}{\int }_a^t\mathit{h}(\mathit{\xi })\frac{(\mathit{t}-\mathit{\xi }{)}^{\mathit{\theta }-1}}{1-\mathit{\theta }}\mathit{d\xi },\\ & \mathit{\theta }\in [0,1].\end{array}$(5)

Definition 5.

(Milici et al., 2018) The constant point ${\delta }^{\ast }$ is an equilibrium point of the Caputo-fractional model, then

(6) ${}^C{D}_t^{\theta }\mathit{\delta }(\mathit{t})=\mathit{h}(\mathit{t},\mathit{\delta }(\mathit{t})),\mathit{\theta }\in [0,1]\text{if and only if}\mathit{h}(\mathit{t},{\delta }^{\ast })=0.$(6)

3. Integer order model formulation

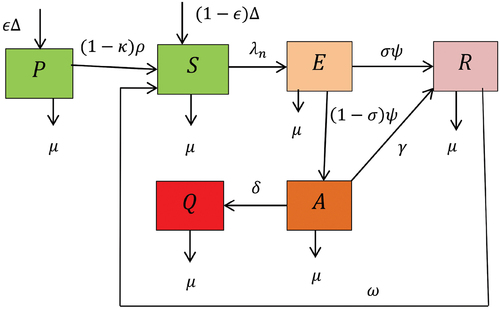
In this section, we have constructed a nonlinear SPEAQR integer order model on negative attitudes of employees towards their workplace to investigate the impacts of protection and improvement strategies on the dissemination dynamics of employees’ negative attitude towards their workplace. To formulate the employees’ negative attitude towards their workplace integer order model we have subdivided the total number of employees’ population N(s) at time s into six mutually exclusive classes such as: S(s) is the number of employees who are free from a negative attitude towards their workplace but at risk for negative attitude towards their workplace, P(s) is the number of employees who are protected against negative attitude towards their workplace, E(s) is the number of employees who are exposed to a negative attitude towards their workplace, A(s) is the number of employees who developed a negative attitude towards their workplace, Q(s) is the number of employees who developed a negative attitude towards their workplace permanently, R(s) is the number of employees that improved their negative attitude towards their workplace through psychological treatment such that:

$\begin{array}{l}\mathit{N}(\mathit{t})=\mathit{S}(\mathit{s})+\mathit{P}(\mathit{s})+\mathit{E}(\mathit{s})+\mathit{A}(\mathit{s})+\mathit{Q}(\mathit{s})+\mathit{R}(\mathit{s}).\end{array}$

For the formulation of the proposed model, employees who are free from negative attitudes towards their workplace but at risk for negative attitudes towards their workplace acquire a negative attitude at the rate given by:

(7) ${\mathit{\lambda }}_n(\mathit{s})=\frac{\mathit{\beta }(\mathit{A}(\mathit{s})+\mathit{\varphi Q}(\mathit{s}))}{N}.$(7)

Basic assumptions: Some portion of the recruited employees who entered into protected class and into the class that contains employees’ who are free from negative attitude towards their workplace but at risk for negative attitude towards their workplace at the rates Δϵ and $\mathrm{\Delta }(1-\mathit{ϵ})$ respectively, where ϵ is a protection coverage and Δ is employees recruitment rate, protection is not 100% efficient and protected individuals lost protection by the rate $(1-\mathit{\kappa })\mathit{\rho }$, where ρ is protection waning rate and κ is portion of protection boosting, the exposed individuals stays hesitant to the negative attitude towards their workplace for a period of $1/\mathit{\psi }$, and some portion of it improved their negative attitude with a probability σ and its complement entered into individuals who developed negative attitude, due to the fading of individuals attitudes, individuals who improved their negative attitudes towards their workplace lose improvement and become at risk for negative attitude towards their workplace at the rate ω, individuals who developed negative attitude can improve from their negative attitude at the rate γ or developed permanent negative attitude towards their workplace at a rate δ, employees are homogeneously mixing in each distinct class, and employees are died by natural mortality rate µ.

Table 1. Explanations of parameters stated in the model

Symbol	Explanation
µ	Human natural mortality rate
Δ	Employees recruitment rate
δ	Progression rate
γ	Improvement(rehabilitation) rate of negative attitude
ρ	Protection lose rate
β	Negative attitude dissemination rate
ϵ	protection coverage
ω	Rehabilitation lose rate
σ	Rehabilitation probability of exposed
ψ	Rate of employees out from exposed group
ϕ	Modification parameter
κ	protection boosting rate

According to the integer order model formulation, Tables 1 and 2, and basic assumptions described above the schematic diagram for employees’ negative attitude towards their workplace dissemination is given by Figure 1.

Table 2. Definitions of state variables

Variable	Definition
S	Employees who are at risk for negative attitude
P	Employees who are protected against negative attitudes
E	Employees who are exposed to negative atittude
A	Employees who have ordinary negative attitude
Q	Employees who have permanent negative attitude
R	Employees rehabilitated from negative attitude

Figure 1. Flow chart of negative attitude employees.

Using the schematic diagram given by Figure 1, the nonlinear ordinary differential equations (model) governed by the basic assumptions described above are represented by:

(8) $\begin{array}{ll}{\displaystyle \frac{\mathit{dS}}{\mathit{dt}}}=& (1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S},\\ {\displaystyle \frac{\mathit{dP}}{\mathit{dt}}}=& \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P},\\ {\displaystyle \frac{\mathit{dE}}{\mathit{dt}}}=& ={\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E},\\ {\displaystyle \frac{\mathit{dA}}{\mathit{dt}}}=& (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A},\\ {\displaystyle \frac{\mathit{dQ}}{\mathit{dt}}}=& \mathit{\delta A}-\mathit{\mu Q},\\ {\displaystyle \frac{\mathit{dR}}{\mathit{dt}}}=& \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R},\end{array}$(8)

with initial data

(9) $\begin{array}{l}\mathit{S}(0)>0,\mathit{P}(0)\ge 0,\mathit{E}(0)\ge 0,\mathit{A}(0)\ge 0,\mathit{Q}(0)\ge 0,\\ \text{and}\mathit{R}(0)\ge 0.\end{array}$(9)

The total sum of each differential equation in (8) gives

(10) $\frac{\mathit{dN}}{\mathit{dt}}=\mathrm{\Delta }-\mathit{\mu N}.$(10)

4. Model derivation in Caputo fractional order operator

In this section, we re-formulate the employees’ negative attitude Caputo fractional order model to observe the memory effects and gain more insights about the employees’ negative attitude dynamics towards their workplace. System (8) in terms of integral form is followed by substituting the value of kernel as a power-law correlation function. After applying the Caputo fractional derivative of $\mathit{\theta }-1$, we have determined the results given by:

(11) $\begin{array}{ll}{}^C{D}_t^{\theta -1}\left[\frac{\mathit{dS}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[(1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}\\ & +(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}],\\ {}^C{D}_t^{\theta -1}\left[\frac{\mathit{dP}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[\mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}],\\ {}^C{D}_t^{\theta -1}\left[\frac{\mathit{dE}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[{\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E}],\\ {}^C{D}_t^{\theta -1}\left[\frac{\mathit{dA}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[(1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A}],\\ {}^C{D}_t^{\theta -1}\left[\frac{\mathit{dQ}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[\mathit{\delta A}-\mathit{\mu Q}],\\ {}^C{D}_t^{\theta -1}\left[\frac{\mathit{dR}}{\mathit{dt}}\right]=& {}^C{D}_t^{\theta -1}{I}_t^{\theta -1}[\mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R}].\end{array}$(11)

Both the left and right sides of (11) are the inverse operators, we have gotten the employees’ negative attitude dynamical system (8) in the Caputo fractional order operator form as:

(12) $\begin{array}{ll}{}^c{D}_t^{\theta }\mathit{S}=& (1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S},\\ {}^c{D}_t^{\theta }\mathit{P}=& \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P},\\ {}^c{D}_t^{\theta }\mathit{E}=& {\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E},\\ {}^c{D}_t^{\theta }\mathit{A}=& (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A},\\ {}^c{D}_t^{\theta }\mathit{Q}=& \mathit{\delta A}-\mathit{\mu Q},\\ {}^c{D}_t^{\theta }\mathit{R}=& \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R}.\end{array}$(12)

The initial conditions for the fractional order derivatives(12) are given as:

(13) $\begin{array}{l}\begin{array}{ll}\mathit{S}(0)\ge 0,& \mathit{P}(0)\ge 0,\mathit{E}(0)\ge 0,\\ \mathit{A}(0)\ge 0,& \mathit{Q}(0)\ge 0,\mathit{R}(0)\ge 0.\end{array}\end{array}$(13)

4.1. Basic properties of the Caputo fractional order model (12)

In the study, since we are dealing with the number of employees that cannot be negative, we have to show there is a non-negative solution in the given region to the fractional order model (12). For various quantitative as well as qualitative aspects, the model we proposed has been analyzed by proving important theorems and incorporating basic algebraic calculations.

Theorem 1.

Solutions to the fractional order model (12) with initial data $\mathit{S}(0)\ge 0,\mathit{P}(0)\ge 0,\mathit{E}(0)\ge 0,\mathit{A}(0)\ge 0,\text{break}\mathit{Q}(0)\ge 0,\mathit{R}(0)\ge 0$ are non-negative.

Proof.

Now we prove the fractional order model (8) solutions non-negativity as follows: Let $\mathit{\tau }=\mathit{sup}\{\mathit{s}>0:\mathit{S}(\mathit{s})>0,\mathit{P}(\mathit{s})>0,\mathit{E}(\mathit{s})>0,\mathit{A}(\mathit{s})>0,\mathit{Q}(\mathit{s})>0,\mathit{R}(\mathit{s})>0\}.$ each functions $\mathit{S}(\mathit{s}),\mathit{P}(\mathit{s}),\mathit{E}(\mathit{s}),\mathit{A}(\mathit{s}),\mathit{Q}(\mathit{s}),$ and R(s) are continuous we observed that τ > 0. Whenever $\mathit{\tau }=\mathrm{\infty }$, then non-negativity holds, but, whenever $0<\mathit{\tau }<+\mathrm{\infty },\mathit{S}(\mathit{\tau })=0$ or $\mathit{P}(\mathit{\tau })=0$ or $\mathit{E}(\mathit{\tau })=0$ or $\mathit{A}(\mathit{\tau })=0$ or $\mathit{Q}(\mathit{\tau })=0$ or $\mathit{R}(\mathit{\tau })=0$.

Let us take the first equation of the model(12) ${}^c{D}_t^{\theta }\mathit{S}=(1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}$. We have determined that

(14) ${}^c{D}_t^{\theta }\mathit{S}>({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}.$(14)

Take the Laplace transform of (14) we have got

(15) $\begin{array}{ll}& \mathcal{L}\{D_t^{\theta }\mathit{S}\}>\mathcal{L}\{({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}\},\\ ⟹& r^{\mathit{\theta }}\mathcal{L}\{\mathit{S}\}-r^{\mathit{\theta }-1}\mathit{S}(0)>({\mathit{\lambda }}_n+\mathit{\mu })\mathcal{L}\{\mathit{S}\},\\ ⟹& (r^{\mathit{\theta }}+({\mathit{\lambda }}_n+\mathit{\mu }))\mathcal{L}\{\mathit{s}\}>r^{\mathit{\theta }-1}\mathit{S}(0),\\ ⟹& \mathcal{L}\{\mathit{S}\}>\frac{{\mathit{r}}^{\mathit{\theta }-1}\mathit{S}(0)}{(r^{\mathit{\theta }}+({\mathit{\lambda }}_n+\mathit{\mu }))}.\end{array}$(15)

Applying the inverse Laplace transform to (15), we have got $\mathit{S}>\mathit{S}(0)E_{\mathit{\theta },1}(-({\mathit{\lambda }}_n+\mathit{\mu })t^{\mathit{\theta }})$, since $\mathit{S}(0)>0$ and $0<E_{\mathit{\theta },1}(-({\mathit{\lambda }}_n+\mathit{\mu })t^{\mathit{\theta }})<1,\mathit{S}>0$ for all t > 0 that is $\mathit{S}(\mathit{\tau })>0$ which is not equal to $\mathit{S}(\mathit{\tau })=0$.

Also from equation two of the dynamical system (12) ${}^c{D}_t^{\theta }\mathit{P}=\mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}$ then we do have

(16) ${}^c{D}_t^{\theta }\mathit{P}\ge -((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}.$(16)

Take the Laplace transform of (16) and we have got

$\begin{array}{ll}{r}^{\mathit{\theta }}\mathcal{L}\{\mathit{P}\}-r^{\mathit{\theta }-1}\mathit{P}(0)& >((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}\mathcal{L}\{\mathit{P}\},\\ \mathcal{L}\{\mathit{P}\}& >\frac{{\mathit{r}}^{\mathit{\theta }-1}\mathit{P}(0)}{r^{\mathit{\theta }}+(1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu }}.\end{array}$

Applying the inverse Laplace transform to (16), we have got $\mathit{P}>\mathit{P}(0)E_{\mathit{\theta },1}(-\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho }{t}^{\mathit{\theta }})$, since $\mathit{P}(0)>0$ and $0<E_{\mathit{\theta },1}(-\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho }{t}^{\mathit{\theta }}<1,\mathit{P}>0$ for all t > 0 that is $\mathit{P}(\mathit{\tau })>0$ which is not equal to $\mathit{P}(\mathit{\tau })=0$.

Similarly, it holds for all $\mathit{E}(\mathit{\tau })>0$ which is not equal to $\mathit{E}(\mathit{\tau })=0,\mathit{A}(\mathit{\tau })>0$ which is not equal to $\mathit{A}(\mathit{\tau })=0,\mathit{Q}(\mathit{\tau })>0$ which is not equal to $\mathit{Q}(\mathit{\tau })=0$ and $\mathit{R}(\mathit{\tau })>0$ which is not equal to $\mathit{R}(\mathit{\tau })=0$. Thus $\mathit{\tau }=\mathrm{\infty }$ and hence all the model (12) solutions are positive for all t > 0 implying that the model has non-negative roots.

Theorem 2.

The set $\mathrm{\Omega }=\{(\mathit{S},\mathit{P},\mathit{E},\mathit{A},\mathit{Q},\mathit{R})R_{+}^6:\mathit{N}\le \frac{\mathrm{\Delta }}{\mu }\}$ bounded in $R_{+}^6$.

Proof.

Considering there is no negative attitude throughout employees and applying Equation (10)(10) $\frac{\mathit{dN}}{\mathit{dt}}=\mathrm{\Delta }-\mathit{\mu N}.$(10) and the proof of non-negativity theorem above, we computed the expression $\frac{\mathit{dN}(\mathit{s})}{\mathit{ds}}\le \mathrm{\Delta }-\mathit{\mu N}(\mathit{s})$. We separate the equation and write as $\int \frac{\mathit{dN}(\mathit{s})}{\mathrm{\Delta }-\mathit{\mu N}(\mathit{s})}\le \int \mathit{ds}$ and after integration, it gives $-\frac{1}{\mu }\mathit{ln}(\mathrm{\Delta }-\mathit{\mu N}(\mathit{s}))\le \mathit{s}+\mathit{k}$, here k is an arbitrary fixed number and when we computed a number of steps we can determine the result $0\le \mathit{N}(\mathit{s})\le \frac{\mathrm{\Delta }}{\mu }$ that means each root of the proposed modeling system positive initial data stated in(13) enter into the set Ω.

4.2. Qualitative analysis of the fractional order model (12)

4.2.1. The dynamical system negative attitude-free equilibrium point

For the employees’ negative attitude-free stationary point of the proposed model (12), we have ${}^c{D}_t^{\theta }\mathit{S}={}^c{D}_t^{\theta }\mathit{P}={}^c{D}_t^{\theta }\mathit{E}={}^c{D}_t^{\theta }\mathit{A}={}^c{D}_t^{\theta }\mathit{Q}={}^c{D}_t^{\theta }\mathit{R}=0.$ Then after some steps of computations the employees’ negative attitude-free equilibrium point of the employees’ negative attitude fractional model (12) is denoted by $E_{NA}^0=(S^0,P^0,E^0,A^0,Q^0,R^0)$ and is given by

(17) $E_{NA}^0=(\frac{(1-\mathit{ϵ})\mathrm{\Delta \mu }+(1-\mathit{\kappa })\mathit{\rho }}{\mathit{\mu }(\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho })},\frac{\mathit{ϵ}\mathrm{\Delta }}{(\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho })},0,0,0,0).$(17)

4.2.2. The fractional order model (12) effective reproduction number

In this manuscript, the stated in reference (Van den Driessche & Watmough, 2002) is used to derive the proposed model reproduction ratio (number) ${\mathcal{R}}_{\mathit{eff}}$ for transmission dynamics of employees’ negative attitude. Employees’ negative attitude reproduction ratio represented by ${\mathcal{R}}_{\mathit{eff}}$ is the estimated number of newly negative attitude employees generated by one negative attitude employee in a susceptible employees community whenever some controlling measures are taken. Here ${\mathcal{R}}_{\mathit{eff}}$ is the dominant eigenvalue in magnitude for the matrix

$\mathit{F}{V}^{-1}=\left[{\displaystyle \frac{\mathit{\partial }{\mathcal{F}}_i(E_{NA}^0)}{\mathit{\partial }{x}_j}}\right]{\left[{\displaystyle \frac{\mathit{\partial }{\mathcal{V}}_i(E_{NA}^0)}{\mathit{\partial }{x}_j}}\right]}^{-1}$ where ${\mathcal{F}}_i$ is the rate at which newly negative attitude infected employees appear in compartment $\mathit{i},V_i$ is the transfer of employees who have a negative attitude from existing class i to another class and $E_{NA}^0$ be the employees’ negative attitude-free stationary point. Let $\mathit{X}={(\mathit{E},\mathit{A},\mathit{Q})}^T$, then we have ${\displaystyle \frac{\mathit{dX}}{\mathit{dt}}}=\mathit{F}-\mathit{V}$ and after some calculations, we determined the following matrices: $\mathit{F}=\left[\begin{array}{lll}0& \frac{\beta S^0}{S^0+P^0}& \frac{\beta \varphi S^0}{S^0+P^0}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$, and $\mathit{V}=\left[\begin{array}{lll}\mathit{\mu }+\mathit{\psi }& 0& 0\\ -(1-\mathit{\sigma })\mathit{\psi }& \mathit{\delta }+\mathit{\gamma }+\mathit{\mu }& 0\\ 0& -\mathit{\delta }& \mathit{\mu }\end{array}\right]$.

The next-generation matrix is of the form

$\begin{array}{l}\mathit{F}{V}^{-1}=\left[\begin{array}{lll}\frac{\beta (1-\sigma )\psi S^0}{D_1(S^0+P^0)}+\frac{\beta (1-\sigma )\psi \delta S^0}{\mathit{\mu }{D}_1(S^0+P^0)}& \frac{\beta S^0}{(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })(S^0+P^0)}+\frac{\beta \varphi \delta S^0}{\mathit{\mu }(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })(S^0+P^0)}& \frac{\beta \varphi S^0}{\mathit{\mu }(S^0+P^0)}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],\end{array}$

where $D_1=(\mathit{\varphi }+\mathit{\mu })(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu }).$ Then the dominant eigenvalue in magnitude of FV⁻¹ known as employees negative-attitude model (12) effective reproduction number given by

(18) $\begin{array}{ll}{\mathcal{R}}_{\mathit{eff}}=& \frac{\beta (1-\sigma )\psi S^0}{D_1(S^0+P^0)}+\frac{\beta (1-\sigma )\psi \delta S^0}{\mathit{\mu }{D}_1(S^0+P^0)}\\ =& \frac{\mathit{\beta }(1-\mathit{\sigma })\mathit{\psi }(\mathit{\varphi \delta }+\mathit{\mu })[(1-\mathit{ϵ})\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho }]}{\mathit{\mu }(\mathit{\mu }+\mathit{\psi })(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })}.\end{array}$(18)

4.2.3. Stability of employees negative attitude-free stationary point

Theorem 3.

Employees’ negative attitude-free stationary point $E_{NA}^0$ of the model (12) has local asymptotic stability whenever ${\mathcal{R}}_{\mathit{eff}}<1$, unsuitability’s whenever ${\mathcal{R}}_{\mathit{eff}}>1$.

Proof 1:

The local asymptotic stability of the employees’ negative attitude-free stationary point of the dynamical system (12) at the employees’ negative attitude-free stationary point

$\begin{array}{ll}{E}_{NA}^0=& (S^0,P^0,E^0,A^0,Q^0,R^0)\\ =& (\frac{(1-\mathit{ϵ})\mathrm{\Delta \mu }+(1-\mathit{\kappa })\mathit{\rho }}{\mathit{\mu }(\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho })},\frac{\mathit{ϵ}\mathrm{\Delta }}{(\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho })},0,0,0,0),\end{array}$

is studied by applying the method stated in the reference (Wondimagegnhu Teklu, 2022). The Jacobian of the proposed model illustrated in (12) at the employees’ negative attitude-free stationary point is presented as

$\begin{array}{l}\mathit{J}(E_{NA}^0)=\left[\begin{array}{llllll}-\mathit{\mu }& \mathit{\varphi }& 0& -\frac{\beta S^0}{S^0+P^0}& -\frac{\beta \varphi S^0}{S^0+P^0}& \mathit{\omega }\\ 0& -((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })& 0& 0& 0& 0\\ 0& 0& -(\mathit{\psi }+\mathit{\mu })& \frac{\beta S^0}{S^0+P^0}& \frac{\beta \varphi S^0}{S^0+P^0}& 0\\ 0& 0& (1-\mathit{\sigma })\mathit{\psi }& (\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })& 0& 0\\ 0& 0& 0& \mathit{\delta }& -\mathit{\mu }& 0\\ 0& 0& \mathit{\sigma \psi }& \mathit{\gamma }& 0& -(\mathit{\omega }+\mathit{\mu })\end{array}\right].\end{array}$

After long calculations the solutions for the characteristics equation of the matrix $\mathit{J}(E_{NA}^0)$ are ${\mathit{\lambda }}_1=-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu }),{\mathit{\lambda }}_2=-(\mathit{\omega }+\mathit{\mu }),{\mathit{\lambda }}_3=-\mathit{\mu }$ and

(19) $a_3{\lambda }^3+a_2{\lambda }^2+a_1\mathit{\lambda }+a_0=0,$(19)

where

$\begin{array}{ll}{a}_3=& 1,a_2=(\mathit{\psi }+\mathit{\mu })+\mathit{\mu }(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu }),\\ a_1=& (\mathit{\psi }+\mathit{\mu })+\frac{\beta \varphi \delta S^0}{S^0+P^0}+(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\\ & (1+\mathit{\mu }+\mathit{\mu }(\mathit{\psi }+\mathit{\mu })(1-{\mathcal{R}}_{\mathit{eff}})),\text{and}\\ a_0=& \mathit{\mu }(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })(\mathit{\psi }+\mathit{\mu })(1-{\mathcal{R}}_{\mathit{eff}}).\end{array}$

Using the local stability criteria stated in (Wondimagegnhu Teklu, 2022) all the eigenvalues of $\mathit{J}(E_{NA}^0)$ are negative whenever ${\mathcal{R}}_{\mathit{eff}}<1$. Thus, the proposed dynamical system (12) has a local asymptotic stable employees’ negative attitude-free stationary point whenever ${\mathcal{R}}_{\mathit{eff}}<1$. Its physical meaning is the employees’ negative attitude towards the workplace can die of the population (whenever the threshold value, ${\mathcal{R}}_{\mathit{eff}}<1$) when the initial data of the dynamical system (8) is in the basin of attraction of the model stationary point ($E_{NA}^0$).

4.2.4. Stability of an endemic stationary point

The negative attitude endemic stationary equilibrium point occurs when the negative attitude exists in the employees’ population. To determine the Caputo fractional order model negative attitude persistence (endemic) stationary point makes the right-hand side of all equations of the system equal to zero. Let $E_{NA}^{\ast }=(S^{\ast },P^{\ast },E^{\ast },A^{\ast },Q^{\ast },R^{\ast })$ be the endemic stationary point of the model (12) and ${\lambda }_n^{\ast }=\frac{\beta }{N}(A^{\ast }(\mathit{t})+\mathit{\varphi }{Q}^{\ast }(\mathit{t})),$ be the employees’ negative attitude infection rate at the endemic stationary point. The proposed model endemic stationary point(s) can derived with respect to ${\lambda }_n^{\ast }=\frac{\beta }{N}(A^{\ast }(\mathit{t})+\mathit{\varphi }{Q}^{\ast }(\mathit{t}))$ at an endemic stationary point. Making the right-hand sides of (8) equal to zero as follows

(20) $\begin{array}{ll}(1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}& =0,\\ \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}& =0,\\ {\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E}& =0,\\ (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A}& =0,\\ \mathit{\delta A}-\mathit{\mu Q}& =0,\\ \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R}& =0.\end{array}$(20)

Solving Equation (20)(20) $\begin{array}{ll}(1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S}& =0,\\ \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P}& =0,\\ {\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E}& =0,\\ (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A}& =0,\\ \mathit{\delta A}-\mathit{\mu Q}& =0,\\ \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R}& =0.\end{array}$(20) we have the employee’s negative attitude endemic point(s)

(21) $\begin{array}{ll}{S}^{\ast }=& \frac{m_8}{m_9{\lambda }_n^{\ast }+m_{10}},P^{\ast }=m_3,E^{\ast }=\frac{m_8{\lambda }_n^{\ast }}{m_{11}{\lambda }_n^{\ast }+m_{12}},\\ A^{\ast }=& \frac{m_5{m}_8{\lambda }_n^{\ast }}{m_{13}{\lambda }_n^{\ast }+m_{14}},Q^{\ast }=\frac{m_5{m}_8{\lambda }_n^{\ast }}{m_{15}{\lambda }_n^{\ast }+m_{16}},\\ R^{\ast }=& \frac{m_5{m}_8\mathit{\gamma }{\lambda }_n^{\ast }+m_6{m}_8{\lambda }_n^{\ast }}{m_4{m}_6{m}_7(m_9{\lambda }_n^{\ast }+m_{10})},\end{array}$(21)

at

(22) $\begin{array}{ll}{m}_1& =(1-\mathit{ϵ})\mathrm{\Delta },m_2=(1-\mathit{\kappa })\mathit{\rho },m_3=\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho },\\ m_4& =\mathit{\mu }+\mathit{\psi },m_5=(1-\mathit{\sigma })\mathit{\psi },\\ m_6& =\mathit{\mu }+\mathit{\gamma }+\mathit{\delta },m_7=\mathit{\mu }+\mathit{\omega },\\ m_8& =m_1{m}_3{m}_4{m}_6{m}_7+m_2{m}_4{m}_6{m}_7\mathit{ϵ}\mathrm{\Delta },\\ m_9& =m_3{m}_4{m}_6{m}_7-m_5\mathit{\omega \gamma }-m_6\mathit{\sigma \omega \varphi },\\ m_{10}& =m_3{m}_4{m}_6{m}_7\mathit{\mu },,m_{11}=m_4{m}_9,\\ m_{12}& =m_4{m}_{10},m_{13}=m_3{m}_4^2{m}_6^2{m}_7-m_4{m}_5{m}_6\mathit{\omega \gamma }\\ & -m_4{m}_6^2\mathit{\sigma \omega \psi },\mathit{and}\\ m_{14}& =m_3{m}_4^2{m}_6^2{m}_7\mathit{\mu },m_{15}=m_{13}\mathit{\mu },\text{and}{m}_{16}=m_{14}\mathit{\mu }.\end{array}$(22)

We substitute (21) with (22) into the expression ${\lambda }_n^{\ast }(\mathit{s})=\frac{\beta }{N}(A^{\ast }(\mathit{s})+\mathit{\varphi }{Q}^{\ast }(\mathit{s})$ with $N^{\ast }=S^{\ast }+P^{\ast }+E^{\ast }+A^{\ast }+Q^{\ast }+R^{\ast }$ and simplifying long computations we have carried out gives us

(23) $a_2{\mathit{\lambda }}_{n^{\ast }}^2+a_1{\lambda }_n^{\ast }+a_0=0,$(23)

at

(24) $\begin{array}{ll}{a}_2=& \mathit{ϵ}\mathrm{\Delta }{m}_4{m}_6{m}_7{m}_9{m}_{13}+m_8{m}_6{m}_7{m}_3{m}_{13}\\ & +m_5{m}_3{m}_8{m}_4{m}_6{m}_7{m}_9\\ & +m_3{m}_5{m}_8{m}_4{m}_6{m}_7{m}_9\mathit{\delta }\\ & +m_3{m}_5{m}_8{m}_{13}\mathit{\gamma }+m_3{m}_6{m}_8{m}_{13}\mathit{\sigma \psi }>0,\\ a_1=& m_8{m}_3{m}_4{m}_6{m}_7{m}_{13}\mathit{\mu }+m_4{m}_6{m}_7{m}_{10}{m}_{13}\mathit{ϵ}\mathrm{\Delta }\\ & +m_4{m}_6{m}_7{m}_9{m}_{14}\mathit{\mu ϵ}\mathrm{\Delta }+m_8{m}_6{m}_7{m}_3{m}_{14}\mathit{\mu }\\ & +m_5{m}_3{m}_8{m}_4{m}_6{m}_7{m}_{10}\mathit{\mu }+m_3{m}_5{m}_8{m}_4{m}_6{m}_7{m}_{10}\mathit{\delta }\\ & +m_{14}{m}_3{m}_5{m}_8\mathit{\gamma \mu }+m_3{m}_6{m}_8{m}_{1}4\mathit{\mu \sigma }\mathrm{\Psi }\\ & -\mathit{\beta }{m}_3{m}_5{m}_8{m}_4{m}_6{m}_7{m}_9\\ & -\mathit{\beta \varphi }{m}_3{m}_5{m}_8{m}_4{m}_6{m}_7{m}_9\mathit{\delta },\text{and}\\ a_0=& \mathit{ϵ}\mathrm{\Delta }{m}_4{m}_6{m}_7{m}_{10}{m}_{14}(1-{\mathcal{R}}_{\mathit{eff}})>0\text{iff}{\mathcal{R}}_{\mathit{eff}}<1.\end{array}$(24)

Since parameters are not negative one can be seen from (22) and (24) that $a_2>0$. Moreover, $a_0>0$ whenever ${\mathcal{R}}_{\mathit{eff}}<1$. Therefore, the potential number of positive real roots in Equation (23)(23) $a_2{\mathit{\lambda }}_{n^{\ast }}^2+a_1{\lambda }_n^{\ast }+a_0=0,$(23) is dependent on the sign of a1. We analyzed it using the rule of signs discovered by Descartes on the polynomial $\mathit{f}(\mathit{x})=a_2{x}^2+a_1\mathit{x}+a_0$ (with $\mathit{x}={\lambda }_n^{\ast }$).

Theorem 4.

The employees’ negative attitude dissemination dynamics model (12)

1. has a unique negative attitude endemic stationary point whenever ${\mathcal{R}}_{\mathit{eff}}<1$ and either of the next two conditions holds

   1. $a_1>0$,

   2. $a_1<0$,

2. could have two endemic equilibrium if ${\mathcal{R}}_{\mathit{eff}}<1$ whenever a1 has negative sign.

Theorem 4 condition (b) suggests the possibility of the existence of multiple endemic equilibria whenever ${\mathcal{R}}_{\mathit{eff}}<1$ (which typically shows the existence of the phenomenon of backward bifurcation (Gumel et al., 2018; Nwankwo & Okuonghae, 2018; Wondimagegnhu Teklu, 2022). The existence of backward bifurcation is characterized by the co-existence of a stable employees’ negative attitude-free stationary point and a stable employee negative attitude endemic stationary point if the associated dynamical system reproduction ratio is below one.

Theorem 5.

The employee negative attitude dissemination dynamics model (12(12) $\begin{array}{ll}{}^c{D}_t^{\theta }\mathit{S}=& (1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S},\\ {}^c{D}_t^{\theta }\mathit{P}=& \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P},\\ {}^c{D}_t^{\theta }\mathit{E}=& {\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E},\\ {}^c{D}_t^{\theta }\mathit{A}=& (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A},\\ {}^c{D}_t^{\theta }\mathit{Q}=& \mathit{\delta A}-\mathit{\mu Q},\\ {}^c{D}_t^{\theta }\mathit{R}=& \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R}.\end{array}$(12) ) shows bifurcation in the backward direction at ${\mathcal{R}}_{\mathit{eff}}=1$ at ${\mathit{\vartheta }}_2>{\mathit{\vartheta }}_1$ where ${\mathit{\vartheta }}_2=2\frac{{\mu }^2(\mathit{\mu }+\mathit{\omega })[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi \delta \mu }{z}_1^0}(1+\frac{\mu }{\delta })$ and ${\mathit{\vartheta }}_1=\frac{\beta (\mu +\omega )(\mu +\delta \varphi )}{\delta (z_1^0+z_2^0)z_1^0}(1+\frac{2\mathit{\mu }}{\mathit{\delta \varphi }})+\frac{{\mu }^2\mathit{\sigma }(\mathit{\mu }+\mathit{\gamma }+\mathit{\delta })+\mathit{\mu }(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi \delta }{z}_1^0}\text{break}(2+\frac{\mu }{\mathit{\delta \varphi }})+\frac{\mu }{z_1^0+z_2^0}(1+\frac{{\mu }^2}{\mathit{\varphi }{\delta }^2}).$

The proof of Theorem 5, based on using center manifold theory stated in Castillo-Chavez & Song (2004) is given in Appendix A. The behavioral implication of Theorem 5 is that the basic requirement to have ${\mathcal{R}}_{\mathit{eff}}<1$, is necessary, but not sufficient for the total control of (or eradication of) the employees’ negative attitude from employer’s in the population.

5. Numerical simulations

5.1. Simulations of the model parameters

In this section of the study, we need to verify the quantitative analyses described and proved in the previous sections and sub-sections, to investigate the parameter effects on the employees’ negative attitude towards their workplace dissemination (or on the model effective reproduction number given by R_eff), and investigate the model state variables behaviors by performing numerical simulations. To make simulations of the proposed fractional order model for achieving the above-mentioned objectives we assumed the reasonable baseline parameter values illustrated as $\mathrm{\Delta }=0.01$, µ = 0.01, κ = 0.9, ψ = 0.1, σ = 0.5, β = 0.5, γ = 0.005, ρ = 0.05, ϕ = 1.75, δ = 0.2.

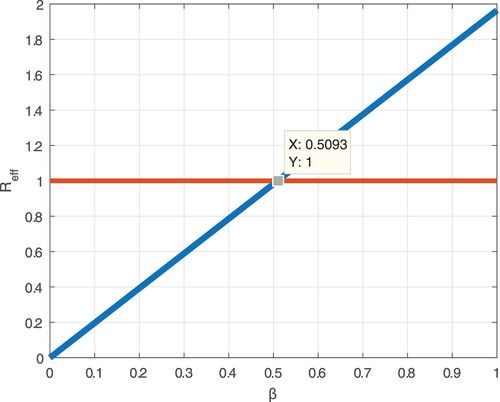
In Figure 2, we show the employees’ negative attitude towards their workplace dissemination rate β influence on the fractional order model effective reproduction number R_eff. The result shows that whenever the value of β increases the dissemination of the negative attitudes of employees toward the workplace goes up. Also, if the information scope is beyond 50%, then the outcome of a negative attitude will flow to a dangerous phase, and the work setting becomes at risk. Thus, implementing the intervention strategies against this negative attitude dispersal is vital to downsize the β value to less than 0.5093.

Figure 2. β vs R_eff.

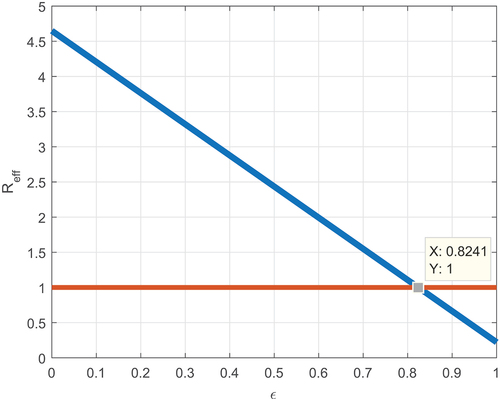
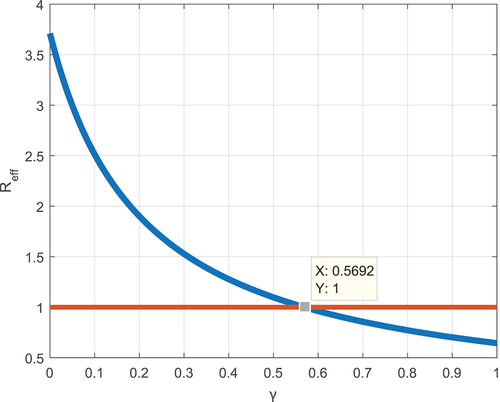
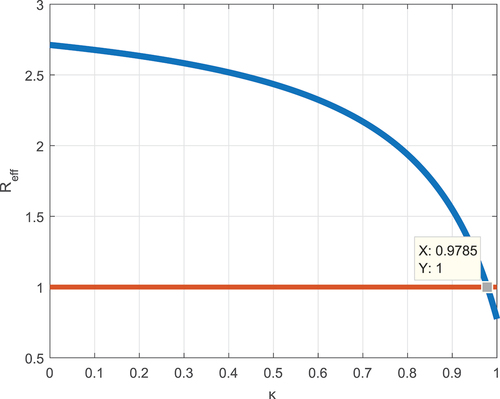
In Figures 3–5, we show the effect of a portion of protection coverage, improvement, and protection boosting strategies against employees’ negative attitude correlating with R_eff. Simulation illustrated by Figure 3 investigated the affinity between ϵ versus R_eff, and the simulation result exhibits approximately surpassing 82.41% protection scope is required to protect the employee from developing a negative attitude towards their workplace. The shield stimulating rate κ has also a significant influence on mitigating the employees’ negative attitude dissemination (see Figure 5). Besides, about 57% of negative attitude improvement strategies enhance the malicious workplace status and decline the wicked attitude persistence (see Figure 4). Therefore, implementing integrated protection and improvement strategies minimizes employees’ negative attitudes toward their workplace and boosts the productivity and quality of the company.

Figure 3. Ε vs R_eff.

Figure 4. γ vs R_eff.

Figure 5. κ vs R_eff.

5.2. Simulations of the model state variables

In this section, we conduct numerical solutions of system (8). For numerical solutions of the proposed system dynamic model, the initial conditions have non-negative values since the number of individuals in each compartment cannot be negative. All numerical computations were performed in MATLAB R2016a using the ode45 embedded Runge-Kutta numerical method. Now, we start to investigate the stability of equilibrium points, examine the influences of various parameters, and explore the impact of intervention strategies. For simulation purposes, we specified the non-negative initial values $(\mathit{S}(0),\mathit{P}(0),\mathit{E}(0),\mathit{A}(0),\mathit{Q}(0),\mathit{R}(0))=(0.96,0.01,0.01,0.01,0.01,0)$ and baseline parameter values $\mathrm{\Delta }=0.01,\mathit{\mu }=0.01,\mathit{\kappa }=0.9,\mathit{\psi }=0.1,\mathit{\sigma }=0.5,\mathit{\beta }=0.5,\mathit{\omega }=0.005,\mathit{\rho }=0.05,\mathit{\varphi }=1.75,\mathit{\delta }=0.2$.

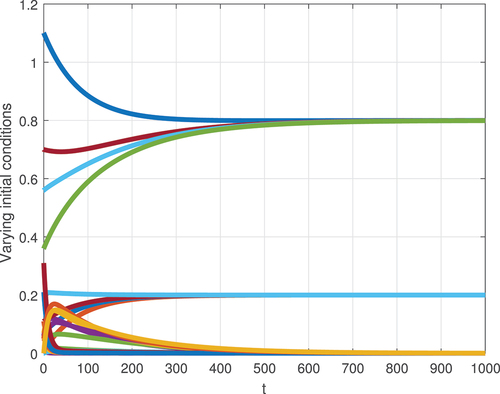
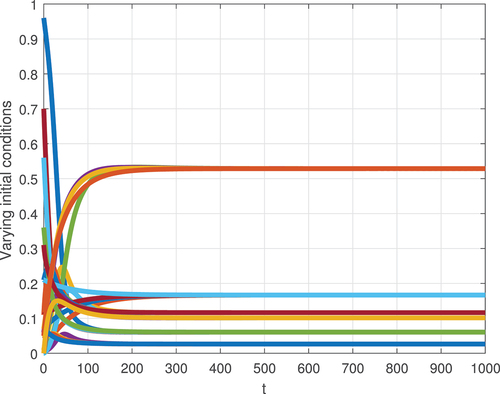
In this first scenario, we illustrate the dynamical anticipation of the model(8) over time when the value of $R_{\mathit{eff}}<1$. This numerical evaluation confirms the theoretical proof of Theorem 3.

The effective reproduction number is computed in the formula (18), and ${\mathcal{R}}_{\mathit{eff}}=0.0629$. The system (8) has only the disease-free equilibrium of $E_{NA}^0=(0.8333,0.1667,0,0,0,0)$. The numerical simulation of system (8) with four distinct initial conditions is exemplified in Figure 6, where all trajectories converge to $E_{NA}^0$. Ultimately, the numerical simulation and the theoretical analysis in Theorem 3 are compatible.

Figure 6. The time series evaluation of system(8) by varying the initial condition and ${\mathcal{R}}_{\mathit{eff}}<1$.

Now, we turn to investigate the stability of negative attitude endemic equilibrium $E_{NA}^{\ast }$ where ${\mathcal{R}}_{\mathit{eff}}>1$ in the same way as carried out above. This numerical evaluation verifies the theoretical proof of Theorem 4.

All the numerical routines in Figure 7 show that numerical solutions trajectories attract toward the endemic stable equilibrium of the system. Figure 7 depicts the time series evaluation of the model (8) with baseline parameter values noted above. Now, a computed in the formula (18), and acquire ${\mathcal{R}}_{\mathit{eff}}=2.5826$, which is greater than one. This estimation implies that two negative attitudes of addiction can pollute more than five susceptible. This time series evaluation shows that the system dynamic solution trajectories are uncertain to their respective extreme values and then asymptotically steady towards the endemic equilibrium $E_{NA}^{\ast }=(0.060,0.1818,0.1213,0.0276,0.5512,0.0576).$

Figure 7. The time series evaluation of system 8(8) $\begin{array}{ll}{\displaystyle \frac{\mathit{dS}}{\mathit{dt}}}=& (1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega R}+(1-\mathit{\kappa })\mathit{\rho P}-({\mathit{\lambda }}_n+\mathit{\mu })\mathit{S},\\ {\displaystyle \frac{\mathit{dP}}{\mathit{dt}}}=& \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })\mathit{P},\\ {\displaystyle \frac{\mathit{dE}}{\mathit{dt}}}=& ={\mathit{\lambda }}_n\mathit{S}-(\mathit{\psi }+\mathit{\mu })\mathit{E},\\ {\displaystyle \frac{\mathit{dA}}{\mathit{dt}}}=& (1-\mathit{\sigma })\mathit{\psi E}-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })\mathit{A},\\ {\displaystyle \frac{\mathit{dQ}}{\mathit{dt}}}=& \mathit{\delta A}-\mathit{\mu Q},\\ {\displaystyle \frac{\mathit{dR}}{\mathit{dt}}}=& \mathit{\gamma A}+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })\mathit{R},\end{array}$(8) by varying the initial condition and ${\mathcal{R}}_{\mathit{eff}}>1$.

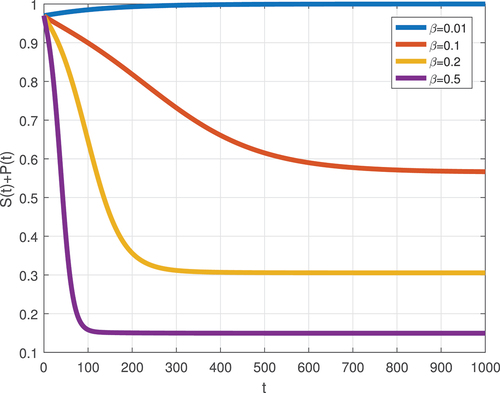
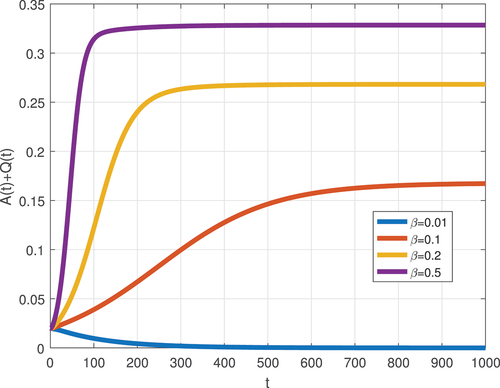
We simulated the model to evaluate the impact of transmission rate β on cumulative susceptible ($\mathit{S}(\mathit{t})+\mathit{P}(\mathit{t})$ and cumulative addicted ($\mathit{A}(\mathit{t})+\mathit{Q}(\mathit{t})$ individuals.

The influence of dissemination rate is evaluated via simulation of the model (8) using the baseline parameter values and various levels of $\mathit{\beta }=0.01,0.1,0.2,0.5$. The results brought, depicted in Figures 8 and 9, show that as the (β value proliferation, hostile attitude dissemination advances to an apex status, and the susceptible individual is consequently addicted to a negative attitude. Also, it has entirely fostered the negative attitude density. From this result, we comprehend that suitable intervention strategies are mandated to remove negative attitudes from the workplace by lowering the contact rate or treating malicious individuals. In our model, implementing efficient protection and treating ordinary negative attitudes toward the workplace are nominee interventions.

Figure 8. The impact of β on the $\mathit{S}(\mathit{t})+\mathit{P}(\mathit{t})$.

Figure 9. The impact of β on the $\mathit{A}(\mathit{t})+\mathit{Q}(\mathit{t})$.

The purpose here is to assess the impact of contemporary employee protection on the propagation dynamics of negative attitudes in the employee community. Hence, employee protection is proposed to minimize susceptibility to a negative attitude, thereby reducing the peril of a negative attitude in the workplace. It is prudent to model the effect of employee protection by reducing the recruitment rate Δ to $(1-\mathit{ϵ})\mathrm{\Delta }$ where $0<\mathit{ϵ}\le 1$ is the protection scope rate of the employee protection strategy embraced. The effect of employee protection is assessed in the absence of any intervention strategy with deviating values of ϵ.

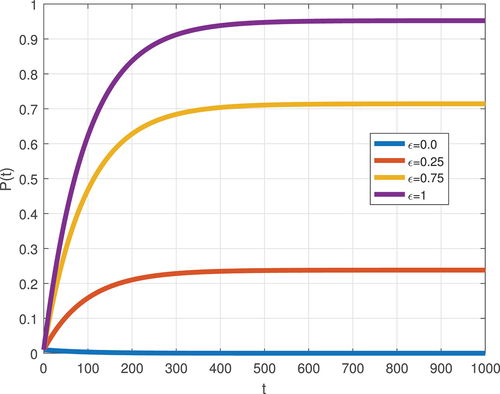
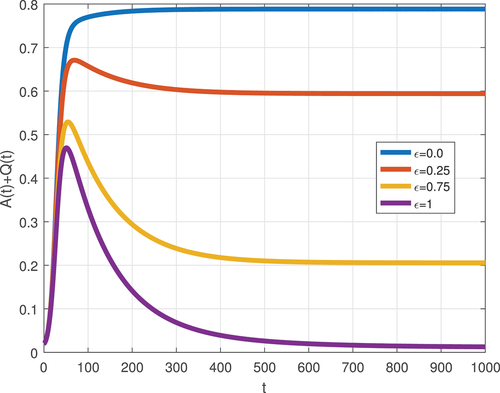
The impact of employee protection is assessed by setting various values of the protection parameter $\mathit{ϵ}=0,0.25,0.75,1$. Figures 10 and Figure 11 depict the solution profiles acquired, showing the worst-case, nearly all workers being contagious by negative attitude and approximately 78% the total employees becomes negative attitude addicted. If implemented at its baseline rate, protection reduces the size of the negative attitude number of new addictions and boosts the protected individuals from zero to 23.8%. Specifically, a 75% refinement in protection intervention will reduce the anticipated number of negative attitudes to approximately from 78% to 20.57% and improves the protected individual up to 71.43%. The result suggests that implementing high coverage protection with appropriate efficiency has a significant role in fruitful workplace establishment.

Figure 10. The impact of ϵ on the P(t).

Figure 11. The impact of ϵ on the $\mathit{A}(\mathit{t})+\mathit{Q}(\mathit{t})$.

An individual negative attitude can have devastating effects on the whole workplace. The encounter of bad attitudes from employees leads to clients’ loss. According to blown task deadlines and incomplete fulfillment of orders, clients aren’t interested in inscribing an agreement with snippy hirelings. The status of negativity in the workplace is like an infection, and even the most promising firms aren’t immune. The negative attitude of employees spoils resilience via declined productivity and quality, the downfall of skill, and client joy. Nevertheless, no one can stop the right attitude of individuals from accomplishing their destination. The result suggests that rescuing employees from poisonous mindsets and enriching optimistic attitudes toward the workplace could reduce the consequences of negative attitudes.

Although this clearly shows that the effectiveness of employee protection has also an undeniable influence.

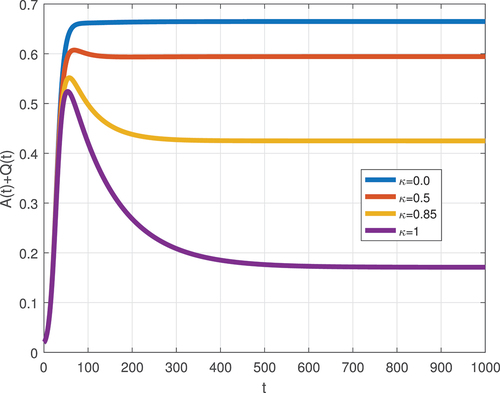
Numerical simulations were further carried out to assess the protection of the role lose boosting rate by running the model (8) with various values of $\mathit{\kappa }=0,0.5,0.85,1$. The results obtained and depicted in Figures 12 and 13 show the number of negative attitudes downsizes whenever we reduce protection waning momentum via protection effectiveness. Further, using efficacious protection, such as protection of efficacy 85%, can decline the negative attitude curve and associated booms in the workplace. Nevertheless, boosting protection efficiency will fail to the ultimate elimination of attitude dissemination (see Figure 13). It is suggested that introducing auxiliary mitigation strategies is also demanded to annihilate hostile attitudes from all employees.

Figure 12. The impact of κ on the P(t).

Figure 13. The impact of κ on the $\mathit{A}(\mathit{t})+\mathit{Q}(\mathit{t})$.

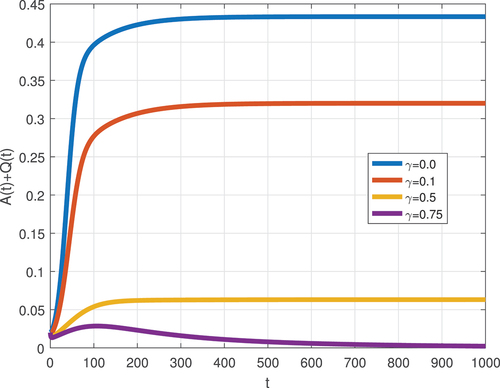
Similarly, we assess the impact of treatment on an ordinary negative attitude to individuals. The time series evaluation is carried out to assess the impact of treatment by varying values of $\mathit{\gamma }=0,0.1,0.5,0.75$. Figure 14 shows that convenient treatment reduces and stems the propagation of negative attitudes among employees. The simulation depicts $50\mathrm{\%}$ treatment of ordinary negative attitude individuals leads to reduce the density of negative attitude from $41\mathrm{\%}$ to 11%. Our simulation results confirm that effective treatment is necessary for containing malicious attitude dissemination. Further, it supports our theoretical analysis, where we ascertained that treatment effectively reduces the reproduction number of the model.

Figure 14. The impact of γ on $\mathit{A}(\mathit{t})+\mathit{Q}(\mathit{t})$.

Intrinsically, negative attitudes exist at a high prevalence, but it’s explicit to acquire cleaned away by negativity. Executives should commence by coaching extraordinary workforce fellows who can assist and guide their colleagues to more cheerful perspectives. Rigorously, the cost of operating negative attitudes at the workplace is an asset that nourishes a restorative rescue. Likewise, positive attitudes can also be transmissible and spread throughout the institution. Therefore, creating a positive attitude in the workplace empowers the rejection ability of employees.

6. Conclusion

In this study, we have constructed and analyzed a six distinct class fractional order model on the employees’ negative attitude towards their workplace, using the Caputo fractional derivative approach. The positivity and boundedness of the model solutions were determined by the Laplace transform method. The negative attitude-free, as well as negative attitude-persistence stationary points of the dynamical system were determined. The model’s negative attitude-free stationary point stability is proved via Routh-Hurwitz stability conditions and is locally asymptotically stable whenever its effective reproduction number is less than one. We have proved that the dynamical system exhibits bifurcation in the backward direction if its effective reproduction number is less than unity which implies that the positive negative attitude-free and negative attitude persistence stationary points co-existed if the corresponding effective reproduction number is below one. Based on the parameters baseline values, we carried out multiple numerical simulations of the model to verify the qualitative results presented in the previous sections, to assess the effectiveness of the protection and improvement (rehabilitation) intervention strategies incorporated in the model construction section, the effectiveness of parameters defined in the dynamical system reproduction number, and to assess the impacts of parameters on state variables of the proposed dynamical system. The simulation graphs demonstrate that all proposed interventions’ parameter values are sensitive to the reproduction number and the negative attitude dissemination rate is the most influential parameter where stakeholders should emphasize to minimize its value by considering suitable intervention measures. The time series evaluation of the model exhibits the same result as the theoretical analysis. The solution trajectories converge toward their respective steady state. We strive to show the impact of dissemination rate β on susceptible, protected, and negative attitude compartments within various values. Numerical simulations illustrated in the absence of a proactive and effective intervention strategy, negative attitudes dissemination in the employees’ workplace could manipulate a perilous work environment. We simulated the roles of employee protection in curtailing the impact of negative attitudes in the workplace. This study shows that employee protection with relevance protection boosting reduces negative attitude dissemination among employees. Ordinary negative attitude improvement (rehabilitation) strategy has a mimic role in the reduction of negative attitude burden and dissemination scope. For instance, this study depicts that negative attitudes can be minimized in the employees’ workplace if the employee protection measure is combined with a negative attitude improvement (rehabilitation) strategy, with moderate protection boosting.

This study did not include the stochastic method, impacts of the work environment, managerial role, leadership style, and real employees’ population primary epidemiological data. Potential researchers can extend this model by using the mentioned limitations of the study.

Author contributions

All authors listed in the manuscript have equal contributions.

Google scholar profile

https://scholar.google.com/citations?user=fEw9ufgAAAAJ&hl=en

Acknowledgements

An older version of this manuscript is published as a preprint entitled ”A nonlinear system dynamics and simulation analysis of fractional order modeling on employees negative attitude towards their workplace with intervention strategies” done by Shewafera Wondimagegnhu Teklu and Dejen Ketema Mamo has been cited in this manuscript with reference [13].

Disclosure statement

The authors of this paper do not have any financial or non-financial interests to disclose.

Supplemental material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/27684830.2024.2322044

Data availability statement

All data generated or analyzed in the process of this study are incorporated in this published paper.

Additional information

Funding

No funds, grants, or other support were received.

Appendix A.

Proof of Theorem 5

Proof.

Let the point given by $E_{NA}^{\ast }=(S^{\ast },P^{\ast },E^{\ast },A^{\ast },\text{break}{Q}^{\ast },R^{\ast })$ be the employee’s negative attitude endemic equilibrium point of the model (8). In this section, we explored the backward bifurcation existence by applying the criteria stated in reference (Castillo-Chavez and Song., 2004)

Let $\mathit{S}=z_1,\mathit{P}=z_2,\mathit{E}=z_3,\mathit{A}=z_4,\mathit{Q}=z_5$, and $\mathit{R}=z_6$ such that $\mathit{N}=z_1+z_2+z_3+z_4+z_5+z_6$. Furthermore, by using vector notation $\mathit{Z}=(z_1,z_2,z_3,z_4,z_5,z_6{)}^T$, the employees negative attitude model (8) is represented by the new system $\frac{\mathit{dZ}}{\mathit{dt}}=\mathit{F}(\mathit{Z})$ with $\mathit{F}=(f_1,f_2,f_3,f_4,f_5,f_6{)}^T$, as follows

(25) $\begin{array}{ll}{\displaystyle \frac{d{z}_1}{\mathit{dt}}}=f_1=& (1-\mathit{ϵ})\mathrm{\Delta }+\mathit{\omega }{z}_6+(1-\mathit{\kappa })\mathit{\rho }{z}_2-({\mathit{\lambda }}_n+\mathit{\mu })z_1,\\ {\displaystyle \frac{d{z}_2}{\mathit{dt}}}=f_2=& \mathit{ϵ}\mathrm{\Delta }-((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })z_2,\\ {\displaystyle \frac{d{z}_3}{\mathit{dt}}}=f_3=& ={\mathit{\lambda }}_n{z}_1-(\mathit{\psi }+\mathit{\mu })z_3,\\ {\displaystyle \frac{d{z}_4}{\mathit{dt}}}=f_4=& (1-\mathit{\sigma })\mathit{\psi }{z}_3-(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })z_4,\\ {\displaystyle \frac{d{z}_5}{\mathit{dt}}}=f_5=& \mathit{\delta }{z}_4-\mathit{\mu }{z}_5,\\ {\displaystyle \frac{d{z}_6}{\mathit{dt}}}=f_6=& \mathit{\gamma }{z}_4+\mathit{\sigma \psi E}-(\mathit{\omega }+\mathit{\mu })z_6,\end{array}$(25)

where ${\mathit{\lambda }}_n(\mathit{t})=\frac{\beta }{N}((z_4(\mathit{t})+\mathit{\varphi }{z}_5(\mathit{t}))$. The Jacobian matrix of the system (25) at the employees negative attitude-free equilibrium point $E_{NA}^0$, denoted by $\mathit{J}(E_{NA}^0)$ is determined as

$\begin{array}{l}\mathit{J}(E_{NA}^0)=\left[\begin{array}{llllll}-\mathit{\mu }& \mathit{\varphi }& 0& -\frac{\beta z_1^0}{z_1^0+z_2^0}& -\frac{\beta \varphi z_1^0}{z_1^0+z_2^0}& \mathit{\omega }\\ 0& -((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })& 0& 0& 0& 0\\ 0& 0& -(\mathit{\psi }+\mathit{\mu })& \frac{\beta z_1^0}{z_1^0+z_2^0}& \frac{\beta \varphi z_1^0}{z_1^0+z_2^0}& 0\\ 0& 0& (1-\mathit{\sigma })\mathit{\psi }& (\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })& 0& 0\\ 0& 0& 0& \mathit{\delta }& -\mathit{\mu }& 0\\ 0& 0& \mathit{\sigma \psi }& \mathit{\gamma }& 0& -(\mathit{\omega }+\mathit{\mu })\end{array}\right].\end{array}$

Consider, ${\mathcal{R}}_{\mathit{eff}}=1$ and let $\mathit{\beta }={\beta }^{\ast }$ be a bifurcation parameter. Using ${\mathcal{R}}_{\mathit{eff}}=1$ we computed the expression ${\mathcal{R}}_{\mathit{eff}}=\frac{{\beta }^{\ast }(1-\mathit{\sigma })\mathit{\psi }(\mathit{\varphi \delta }+\mathit{\mu })[(1-\mathit{ϵ})\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho }]}{\mathit{\mu }(\mathit{\mu }+\mathit{\psi })(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })}=1$ and solving for ${\beta }^{\ast }$ we have got ${\beta }^{\ast }={\beta }^{\ast }=\frac{\mathit{\mu }(\mathit{\mu }+\mathit{\psi })(\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })}{{\beta }^{\ast }(1-\mathit{\sigma })\mathit{\psi }(\mathit{\varphi \delta }+\mathit{\mu })[(1-\mathit{ϵ})\mathit{\mu }+(1-\mathit{\kappa })\mathit{\rho }]}$. Then

$\begin{array}{l}{J}_{{\beta }^{\ast }}=\left[\begin{array}{llllll}-\mathit{\mu }& \mathit{\varphi }& 0& -\frac{{\beta }^{\ast }{z}_1^0}{z_1^0+z_2^0}& -\frac{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}{z_1^0+z_2^0}& \mathit{\omega }\\ 0& -((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })& 0& 0& 0& 0\\ 0& 0& -(\mathit{\psi }+\mathit{\mu })& \frac{{\beta }^{\ast }{z}_1^0}{z_1^0+z_2^0}& \frac{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}{z_1^0+z_2^0}& 0\\ 0& 0& (1-\mathit{\sigma })\mathit{\psi }& (\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })& 0& 0\\ 0& 0& 0& \mathit{\delta }& -\mathit{\mu }& 0\\ 0& 0& \mathit{\sigma \psi }& \mathit{\gamma }& 0& -(\mathit{\omega }+\mathit{\mu })\end{array}\right].\end{array}$

One can verify that the new system (25), with $\mathit{\beta }={\beta }^{\ast }$, has a non-hyperbolic equilibrium point where the linearized system of (25) all eigenvalues except a simple eigenvalue with zero real part have negative real parts. The Jacobian of the dynamical system (8) at the employees negative attitude-free stationary point $\mathit{J}(E_{NA}^0$ at $\mathit{\beta }={\beta }^{\ast }$ represented by $J_{{\beta }^{\ast }}$ have a single zero eigenvalue and the remaining eigenvalues with negative real parts. Furthermore, using the method mentioned in the reference Dynamical models of tuberculosis (Castillo-Chavez and Song., 2004) we have shown the phenomenon of the backward bifurcation existence of the dynamical system (8) at ${\mathcal{R}}_{\mathit{eff}}=1$.

Possible eigenvectors for the matrix $J_{{\beta }^{\ast }}$: If ${\mathcal{R}}_{\mathit{eff}}=1$, then right eigenvectors for the matrix $J_{{\beta }^{\ast }}$ corresponding to the zero eigenvalues denoted by $\mathit{u}=(u_1,u_2,u_3,u_4,u_5,u_6{)}^T$ are obtained as

(26) $\begin{array}{l}\left(\begin{array}{llllll}-\mathit{\mu }& \mathit{\varphi }& 0& -\frac{{\beta }^{\ast }{z}_1^0}{z_1^0+z_2^0}& -\frac{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}{z_1^0+z_2^0}& \mathit{\omega }\\ 0& -((1-\mathit{\kappa })\mathit{\rho }+\mathit{\mu })& 0& 0& 0& 0\\ 0& 0& -(\mathit{\psi }+\mathit{\mu })& \frac{{\beta }^{\ast }{z}_1^0}{z_1^0+z_2^0}& \frac{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}{z_1^0+z_2^0}& 0\\ 0& 0& (1-\mathit{\sigma })\mathit{\psi }& (\mathit{\delta }+\mathit{\gamma }+\mathit{\mu })& 0& 0\\ 0& 0& 0& \mathit{\delta }& -\mathit{\mu }& 0\\ 0& 0& \mathit{\sigma \psi }& \mathit{\gamma }& 0& -(\mathit{\omega }+\mathit{\mu })\end{array}\right)\left(\begin{array}{l}{u}_1\\ u_2\\ u_3\\ u_4\\ u_5\\ u_6\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right).\end{array}$(26)

The right eigenvectors corresponding to the zero eigenvalues is determined by solving the system (26) and are presented by

$\begin{array}{ll}{u}_1=& [-\frac{\mathit{\mu \sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mu \alpha \gamma }{\mathit{\alpha \delta }{\mathit{\omega }}_2}\\ & +\frac{\mathit{\mu }{\mathit{\omega }}_2(\mathit{\mu }+{\omega }_1)(\mathit{\mu }+{\omega }_2)[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma \alpha }]}{\mathit{\alpha \delta }{\omega }_2\mathit{\mu }{\omega }_2(\mathit{\mu }+{\omega }_1+{\omega }_2)}\\ & -\frac{{\mathit{\beta }}^{\ast }{\omega }_2(\mathit{\mu }+{\omega }_1)[\mathit{\mu }+\mathit{\delta \varphi }]}{{\mathit{\delta \mu }{\mathit{\omega }}_2(\mathit{\mu }+{\omega }_1+{\omega }_2)(\mathit{z}}_1^0+z_2^0)}]u_5,\\ u_2=& 0,u_3=\frac{\mathit{\mu }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })}{\mathit{\alpha \delta }}{u}_5,u_4=\frac{\mu }{\delta }{u}_5,u_5=u_5>0,\\ u_6=& [\frac{\mathit{\mu \sigma }{\mathit{\omega }}_2(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })(\mathit{\mu }+{\omega }_2)}{\mathit{\alpha \delta }{\omega }_2\mathit{\mu }(\mathit{\mu }+{\omega }_1+{\omega }_2)}+\frac{\mathit{\gamma \mu }{\mathit{\omega }}_2(\mathit{\mu }+{\omega }_2)}{\mathit{\delta }{\omega }_2\mathit{\mu }(\mathit{\mu }+{\omega }_1+{\omega }_2)}\\ & -\frac{{\mathit{\beta }}^{\ast }\mathit{\mu }{\omega }_2+{\beta }^{\ast }\mathit{\delta \varphi }{\omega }_2}{{\mathit{\delta \mu }(\mathit{\mu }+{\mathit{\omega }}_1+{\omega }_2)(\mathit{z}}_1^0+z_2^0)}]u_5.\end{array}$

In the same manner, the left eigenvectors corresponding to the zero eigenvalues at $\mathit{\beta }={\beta }^{\ast }$ are presented by $\mathit{v}=(v_1,v_2,v_3,v_4,v_5,v_6)$ or ${\left(\begin{array}{l}{\mathit{v}}_1\\ v_2\\ v_3\\ v_4\\ v_5\\ v_6\end{array}\right)}^{\mathit{T}}$ are determined by

(27) ${\left(\begin{array}{l}{\mathit{v}}_1\\ v_2\\ v_3\\ v_4\\ v_5\\ v_6\end{array}\right)}^{\mathit{T}}\ast \left(\begin{array}{llllll}-(\mathit{\mu }+{\omega }_2)& \mathit{\rho }& 0& -\frac{{\beta }^{\ast }}{z_1^0+z_2^0}& -\frac{{\mathit{\beta }}^{\ast }\mathit{\varphi }}{z_1^0+z_2^0}& {\omega }_1\\ 0& -(\mathit{\alpha }+\mathit{\rho })& 0& 0& 0& 0\\ 0& 0& -(\mathit{\mu }+\mathit{\alpha }+\mathit{\sigma })& \frac{{\beta }^{\ast }}{z_1^0+z_2^0}& \frac{{\mathit{\beta }}^{\ast }\mathit{\varphi }}{z_1^0+z_2^0}& 0\\ 0& 0& \mathit{\alpha }& -(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })& 0& 0\\ 0& 0& 0& \mathit{\delta }& -\mathit{\mu }& 0\\ {\omega }_2& 0& \mathit{\sigma }& \mathit{\gamma }& 0& -(\mathit{\mu }+{\omega }_1)\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right)$(27)

Similarly, the left eigenvectors corresponding to the zero eigenvalues is determined by solving the system (27) and are presented by

$v_1=v_2=v_6=0$, $v_3=\frac{\mu (z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}{v}_5$,$v_4=\frac{\mu (\mu +\psi )(z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}$, and $v_5=v_5>0$. The non-zero second-order partial derivatives at negative attitude-free stationary point represented by $E_{\text{NA}}^0=(\frac{\mathrm{\Delta }(1-\mathit{\epsilon })\mathit{\mu }+\mathit{\rho })}{\mathit{\mu }(\mathit{\mu }+\mathit{\rho })},\frac{\mathit{\epsilon }\mathrm{\Delta }}{\mathit{\mu }+\mathit{\rho }},0,0,0,0)$ of the system (26) are given by

$\begin{array}{ll}\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial }{x}_1}=& \frac{\beta }{z_1^0+z_2^0},\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial }{x}_1}=\frac{\beta \varphi }{z_1^0+z_2^0},\\ \frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{{\mathit{x}}_4}^2}=& \frac{-2\beta z_1^0}{{{(z}_1^0+z_2^0)}^2},\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{{\mathit{x}}_5}^2}=\frac{-2\beta \varphi z_1^0}{{{(z}_1^0+z_2^0)}^2},\\ \frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial \beta }}=& \frac{Z_1^0}{z_1^0+z_2^0},\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial \beta }}=\frac{\varphi Z_1^0}{z_1^0+z_2^0}.\end{array}$

Since all the parameters are non-negative the constants a and b known as bifurcation coefficients can be computed as

(28) $\begin{array}{ll}\mathit{a}=& \sum _{\mathit{i},\mathit{j}}^6{v}_3{u}_{\mathit{i}}{u}_{\mathit{j}}\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_{\mathit{i}}\mathit{\partial }{x}_{\mathit{j}}}=2v_3{u}_4{u}_1\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial }{x}_1}\\ & +2v_3{u}_5{u}_1\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial }{x}_1}+v_3{u}_4{u}_4\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{{\mathit{x}}_4}^2}+v_3{u}_5{u}_5\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{{\mathit{x}}_5}^2},\\ =& u_5^2{v}_5[-2\frac{{\mathit{\mu }}^3\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+{\mu }^3(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi }{z}_1^0}\\ & +2\frac{{\mathit{\mu }}^3(\mathit{\mu }+\mathit{\omega })\mathit{\mu }[\mathit{\sigma \psi }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi \mu }(\mathit{\mu }+\mathit{\omega })z_1^0}\\ & -2\frac{{\mathit{\mu }}^2{\beta }^{\ast }(\mathit{\mu }+\mathit{\omega })[\mathit{\mu }+\mathit{\delta \varphi }]}{{{\mathit{\delta }}^2\mathit{\mu }(\mathit{\mu }+\mathit{\omega })(\mathit{z}}_1^0+z_2^0)\mathit{\varphi }{z}_1^0}\\ & -2\frac{{\mathit{\mu }}^2\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\mu }(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi \delta }{z}_1^0}\\ & +2\frac{{\mathit{\mu }}^2(\mathit{\mu }+\mathit{\omega })\mathit{\mu }[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi \sigma \mu }(\mathit{\mu }+\mathit{\omega })z_1^0}\\ & -2\frac{{\mathit{\beta }}^{\ast }[\mathit{\mu }+\mathit{\delta \varphi }]}{{\delta (z}_1^0+z_2^0)z_1^0}-2\frac{{\mu }^3}{\mathit{\varphi }{\delta }^2(z_1^0+z_2^0)}-2\frac{\mu }{(z_1^0+z_2^0)}],\\ =& u_5^2{v}_5[2\frac{{\mathit{\mu }}^2(\mathit{\mu }+\mathit{\omega })[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi \delta }(\mathit{\mu }+\mathit{\omega })z_1^0}\\ & +2\frac{{\mathit{\mu }}^3(\mathit{\mu }+\mathit{\omega })[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi }(\mathit{\mu }+\mathit{\omega })z_1^0}\\ & -2\frac{{\mathit{\mu }}^2{\beta }^{\ast }(\mathit{\mu }+\mathit{\omega })[\mathit{\mu }+\mathit{\delta \varphi }]}{{{\mathit{\delta }}^2\mathit{\mu }(\mathit{z}}_1^0+z_2^0)\mathit{\varphi }{z}_1^0}\\ & -2\frac{{\mathit{\mu }}^2\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\mu }(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi \delta }{z}_1^0}\\ & -\frac{{\mathit{\mu }}^3\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+{\mu }^3(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi }{z}_1^0}-\frac{{\mathit{\beta }}^{\ast }\mathit{\mu }[\mathit{\mu }+\mathit{\delta \varphi }]}{{\delta (z}_1^0+z_2^0)z_1^0}\\ & -\frac{{\mu }^3}{\mathit{\varphi }{\delta }^2(z_1^0+z_2^0)}-\frac{\mu }{(z_1^0+z_2^0)}],\\ =& u_5^2{v}_5[{\mathit{\vartheta }}_2-{\mathit{\vartheta }}_1],\end{array}$(28)

where

$\begin{array}{ll}{\mathit{\vartheta }}_2=& 2\frac{{\mathit{\mu }}^2(\mathit{\mu }+\mathit{\omega })[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi \delta \mu }{z}_1^0}\\ & +2\frac{{\mathit{\mu }}^3(\mathit{\mu }+\mathit{\omega })[\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\gamma }(1-\mathit{\sigma })\mathit{\psi }]}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi \mu }{z}_1^0}\end{array}$

and

$\begin{array}{ll}{\mathit{\vartheta }}_1=& 2\frac{{\mathit{\mu }}^2{\beta }^{\ast }(\mathit{\mu }+\mathit{\omega })[\mathit{\mu }+\mathit{\delta \varphi }]}{{{\mathit{\delta }}^2\mathit{\mu }(\mathit{z}}_1^0+z_2^0)\mathit{\varphi }{z}_1^0}\\ & +2\frac{{\mathit{\mu }}^2\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+\mathit{\mu }(1-\mathit{\sigma })\mathit{\psi \gamma }}{(1-\mathit{\sigma })\mathit{\psi \delta }{z}_1^0}\\ & +\frac{{\mathit{\mu }}^3\mathit{\sigma }(\mathit{\mu }+\mathit{\delta }+\mathit{\gamma })+{\mu }^3\mathit{\alpha \gamma }}{(1-\mathit{\sigma })\mathit{\psi }{\delta }^2\mathit{\varphi }{z}_1^0}+\frac{{\mathit{\beta }}^{\ast }(\mathit{\mu }+{\omega }_1)[\mathit{\mu }+\mathit{\delta \varphi }]}{{\delta (z}_1^0+z_2^0)z_1^0}\\ & +\frac{{\mu }^3}{\mathit{\varphi }{\delta }^2(z_1^0+z_2^0)}+\frac{\mu }{(z_1^0+z_2^0)}\end{array}$

Furthermore

$\begin{array}{ll}\mathit{b}& =\sum _{\mathit{i},\mathit{k}=1}^5{v}_{\mathit{k}}{u}_{\mathit{i}}\frac{{\mathit{\partial }}^2{f}_{\mathit{k}}}{\mathit{\partial }{x}_{\mathit{i}}\mathit{\partial \beta }}\left(E_A^0\right)=\sum _{\mathit{i}=1}^5{v}_3{u}_{\mathit{i}}\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_{\mathit{i}}\mathit{\partial \beta }}\\ & =v_3{u}_4\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial \beta }}+v_3{u}_5\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial \beta }},\\ & =\frac{\mu (z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}\frac{\mu }{\delta }\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial \beta }}{u}_5{v}_5+\frac{\mu (z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial \beta }}{v}_5{u}_5,\\ & =v_5{u}_5[\frac{\mu (z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}\frac{\mu }{\delta }\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_4\mathit{\partial \beta }}+\frac{\mu (z_1^0+z_2^0)}{{\beta }^{\ast }\mathit{\varphi }{z}_1^0}\frac{{\mathit{\partial }}^2{f}_3}{\mathit{\partial }{x}_5\mathit{\partial \beta }}],\\ & =v_5{u}_5[\frac{{\mu }^2}{{\beta }^{\ast }\mathit{\varphi \delta }}+\frac{\mu }{{\beta }^{\ast }}]>0.\end{array}$

Since b is positive based on the criteria stated in the reference (Castillo-Chavez and Song., 2004) the dynamical system in (12) exhibits the phenomenon of bifurcation in the backward direction whenever the coefficient, a, presented in (12) is positive, ${\mathit{\vartheta }}_2>{\mathit{\vartheta }}_1$ and ${\mathcal{R}}_{\mathit{eff}}=1$.