?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.ABSTRACT
In this paper, we analyze the Achilles-Tortoise paradox, which denies the overtaking of the slowest runner (Tortoise) by the quickest runner (Achilles) because the pursuer must first reach the point whence the pursued started, so the slower must always hold the lead. The paradox translates into a requirement for the quicker to complete one by one an infinite sequence of distinct runs in a finite time to overtake the slower. This feat is impossible because the infinite sequence of distances contains no final distance to run, and the time to complete such a feat is not enough. However, we know better that in a race, the quickest always overtakes the slowest. Then why does the argument say otherwise? There should be logical flaws in its argumentation. Therefore, after an analysis of the paradox, we investigate the existence of such a flaw that exists in the argument itself or in the inferences its premises make. In addition to this, we present the new mathematical solution based on open balls in real Euclidean space, which shows that only a finite number of runs are needed by the quickest to overtake the slowest.
1. Introduction
A long time ago before Christ Era, Zeno of Elea raised some questions about the possibility of motion. He constructed arguments which were designed to reject the existence of motion: that any claim to the contrary was an illusion. One of such arguments is concerning the race involving the fastest runner (Achilles, for instance) who tries to overtake the slowest runner (Tortoise, for example) that is slowly crawling away from him. Zeno claims that Achilles will never overtake the Tortoise because at all times, the Tortoise is always ahead of Achilles. The approximate form of the Achilles—Tortoise Paradox as it appears in Barnes (Citation1991: 110) states that:
In a race the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. (Aristotle Physics, Book VI, Chap. 9, 239b14–29)
Achilles and Tortoise take the positions of the quickest and the slowest runner respectively. Let and
denote the respective nth position of Achilles and the Tortoise for each
(see Figure ).
For Achilles to catch the Tortoise, he will have to reach the position T0, where the Tortoise currently is. However, by the time Achilles gets there, the Tortoise will have crawled to a new position T1. Achilles will then have to reach this new position. By the time Achilles reaches T1, the Tortoise will have moved on to yet another position T2, and so on forever. In each moment Achilles completes the distance between them, the Tortoise—at the same time—will be adding a new lead, however small, for Achilles to catch up again. This process is endless and produces an infinite number of leads, which is too much even for Achilles to complete. Zeno claims that Achilles will never catch the Tortoise because the Tortoise is always ahead of him. This conclusion is paradoxical, as we know better that Achilles will easily overtake Tortoise.
Many solutions have been offered in resolving the Achilles-Tortoise paradox, but none has survived. Every time the solution was given, it was criticized and ultimately rejected. Although there is not a single solution that is accepted to all (Shamsi, Citation1972: 125), there is one most celebrated solution called the Standard Solution that has convinced many but all scholars over a century now (Dowden, Citation2010). We will briefly discuss the body of this sol subsection.
1.1. The standard solution and the Achilles-Tortoise paradox
The Standard Solution is claimed by many scholars, notably by Russell (Citation1914, Lecture 6) and Grünbaum (Citation1967) to have resolved the paradox. We will show that the theses upon which the body of this solution is built do not actually address the heart of the paradox.
According to the Standard Solution, Zeno is thought to assert that Achilles will never overtake the Tortoise because there is too far to run, or there is not enough time, or there are too many places to go, or there is no final step, or there are too many tasks. The advocates of the Standard Solution claim that all such allegations are fallacious. Below are the theses upon which the Standard Solution is built:
| S1. | It presupposes differential calculus and classical mechanics. | ||||
| S2. | The runners path is a physical continuum which is completed using a positive finite speed. | ||||
| S3. | Durations, distances, and line segments are all linear continua composed of indivisible points. | ||||
| S4. | Both Achilles and Tortoise run at constant speeds. | ||||
| S5. | Achilles and Tortoise are assumed to be points without parts. | ||||
The standard solution then uses these theses to question the assertions and inferences made by Zeno. On the assertion that there is too far to run: the Standard Solution claims that although Zeno was correct in saying that at every point or instant before reaching the goal there is always some distance ahead to cover, this does not imply that the goal is never reached. The claim here is that although there are infinite number of diminishing positive leads, their sum is finite (constant speeds (Thesis ) generate a monotone decreasing geometric sequence of leads). The same reasoning holds on the assertions that there is not enough time or there are too many places to go. The detailed analysis of the Standard Solution is beautifully explained by Dowden (Citation2010); Grünbaum (Citation1967) and Russell (Citation1914). The Standard Solution is backed up by the creation of the foundations of analysis developed in the nineteenth century by the works of Georg Cantor, Dedekind, Lebesgue, Weierstrass, Cauchy, and others.
1.2. Critiques of the standard solution
In this section, we show the severe logical difficulties the Standard Solution poses. It finds Zeno’s argument at no faulty and proceeds by accepting all premises of the paradox: that is, maintaining the starts and stops in a path. We shall now visit one by one the mistakes committed in this solution:
| C1. | On thesis | ||||
| C2. | On the Infinite sum and the Completion of Infinitely Many Tasks: The advocates of the Standard Solution postulate that although there are infinite number of finite distances for Achilles to cover, they, using classical analysis, claim that their sum is finite, and thus Achilles can easily overtake the Tortoise in a finite time. This allegation is quite debatable. The sum of infinite number of positive distances may or may not be finite: this depends on the mathematical rule that generates such distances. At this point, it is fallacious to dismiss Zeno’s conclusion. Moreover, although the infinite number of distances may sum up to a finite number, it does not mean that we have been physically able to add all terms of the infinite sequence. That sum is just the supremum of the sequence of partial sums. The so-called ”sum‘ is merely the number closer to the ’actual sum” of the infinite series within a certain tolerance. The process of adding distances one by one is equivalent to the action or task of traversing such distances one by one: which is actually what Achilles is called to perform if Zeno’s instructions are accepted. Therefore, Achilles is called to complete an infinite number of tasks one by one, each requiring a certain amount of time to complete. Can he complete this task? To answer this, we need to prove that there is a final task that Achilles will perform to win the race. Now this is the problem, as the sequence of tasks is predetermined by the endless leads established by the Tortoise. The final distance, no matter how small the gap between the two runners becomes, does not exist. The supremum of the sequence of partial sums of distances should, by any means, not be confused with the final term of the sequence of distances. Proceeding in this way, we see that the final task does not exist as well. There is no, in the physical world or in logic, a physical task that approximates or bounds the sequence of tasks, even if their completion each needs less and less positive time. This is the huge oversight committed by Russell (Citation1914) who in his Lectures 6 and 7, dismisses Zeno’s conclusion simply by contenting himself to the view that it is not true that infinite number of infinitesimal distances makes up an infinitely long distance. He merely confuses the infinite sequence of numbers generated by some mathematical rule with the infinite sequence of physical tasks. Again, we see that the so-called infinite sum, if done by adding its terms one by one instead of taking limits, is difficult to justify its attainment. | ||||
| C3. | About Achilles and Tortoise being assumed as indivisible points: This is the most articulate blunder committed by advocates of the Standard Solution. In Zeno’s words, while stating the paradox of plurality, postulates that | ||||
It is now evident that some of the assumptions and allegations upon which the Standard Solution of Achilles-Tortoise Paradox is built are inconsistent and lead to many questionable premises. However, the Standard Solution beautifully tells us where and when Achilles will overtake the Tortoise. It takes Zeno’s instructions of the argument to be of no fault even though it does not answer Zeno’s central problem he was addressing: the problem of completing infinite number of physical tasks one by one in a finite time.
Black (Citation1951: 101) pointed out that the popular mathematical refutation of Zeno’s Achilles-Tortoise paradox will not do, because it simply assumes that Achilles can perform an infinite sequence of acts. The problem, to be specific, is whether it even makes sense to think that Achilles has completed an infinite sequence of runs (Salmon, Citation1970: 140–141). Black maintains that the infinite sequence of acts is self-contradictory. Of the same stance are Thomson (Citation1954: 13), Weyl (Citation1949: 41–42), Benacerraf (Citation1962), and Alba (Citation1996: 299), who argue that mathematical solutions to the paradox miss and will always miss the point of Zeno’s argument; for they do not actually touch Zeno’s argument and make no metaphysical contribution to the paradox.
We believe that there is no scholar today who would accept Zeno’s conclusion. However, the logical difficulties raised by Zeno cannot be simply dismissed. Wisdom (Citation1952), Black (Citation1951: 91), and Thomson (Citation1954) argue that it would be a waste of time to prove that Achilles will overtake the Tortoise, as everyone knows this already, and instead the confusion arises because the conclusion of Zeno’s argument is absurd. There has to be a misdescription of the situation that produces this paradox. What is needed then is the analysis of the argument. Our contention is thus to analyze and find the mistake committed in this argument: for if we accept Zeno’s instructions, we must then agree with his conclusion.
1.3. Statement of the problem
The difficulties Zeno raised were far from being trivial—that motion is an illusion. For if we argue in contrary, we owe an account of showing what is wrong with Zeno’s argument (Dowden, Citation2010). These difficulties in Zeno’s argument stem from the fact that Achilles, according to Zeno’s assumptions, will never overtake the Tortoise because he is required to travel an infinite sequence of distances one by one. There is no final distance in such an infinite sequence and thus no final step Achilles can take to win a race. It is even worse to believe that an infinite sequence of physical tasks can be completed because there is not enough time to finish such a never-ending process. Although Zeno’s conclusion seems to be obviously false, there has been no universal agreement on just what was wrong with his argument (Benacerraf, Citation1962: 765). The mathematical literature of today and the scientific literature in general are far less engaged with this issue (Dowden, Citation2010). This leaves the problem unsolved. The purpose of this paper is therefore to analyse and investigate the wording of the Achilles-Tortoise paradox and single out the contradictory premises which dictate the logic and nest the aforementioned difficulties. We will then provide the new mathematical solution to the paradox which does not call for the completion of infinite number of runs.
1.4. Research objectives
The following are the specific objectives of this research paper.
To analyze Zeno’s Achilles-Tortoise paradox.
To investigate the logic flaw behind the formulation of the Achilles-Tortoise paradox that results in a contradictory conclusion.
To develop a new mathematical solution in resolving the paradox.
2. Methods
In general, we will use logic and classical analysis to investigate the implication(s) of every premise in the argument. The argument will be broken down into simple premises; study the implication and correctness of each premise. We will then investigate the truth of the compound argument. Since the conclusion of the argument is false, the whole argument is false. There must be at least one premise that leads to an incorrect and false inference. Classical analysis will be applied mainly on the properties of linear continuum and the convergence of sequence of real numbers. Specifically, definition 2.1 and, Theorems 2.1 and 2.3 will be used in analysis of the argument (objective (i)) and in answering the objective (ii). Theorem 2.2 and the concept of open balls in a real Euclidean space will be used to answer the objective (iii).
Definition 2.1.
One runner is quicker than the other if
the quicker moves a strictly greater distance than the slower in the less amount of time, or
the quicker moves a distance equal to the slower in the less amount of time, or
the quicker moves a strictly greater distance than the slower in the same amount of time,
The two runners will be said to have equal speed if both cover equal distance in equal amount of time.
Theorem 2.1.
There does not exist a positive real number that is smaller than every positive real number.
Proof.
Suppose such number exists. Let be an interval on
for any δ > 0 and let
. By definition, we have
for all
. If we take
, we have
and
. This contradicts the hypothesis that
.
Theorem 2.2.
(Monotone Convergence Theorem (Bartle & Sherbert, Citation2000: 69))
A monotone sequence of real numbers is convergent if and only if it is bounded. Moreover,
If
is a bounded increasing sequence, then
If
is a bounded decreasing sequence, then
That which exists has some size and thickness (Simplicius a, Citation1995) and, if set in motion, such thing will initially cover a space less than or equal to its own whole space it occupies (Barnes, Citation1991: 112). The following theorem, based on the existence of things, proves the nonexistence of a self-motion for an indivisible point set.
Theorem 2.3.
An indivisible point-set has no self-motion.
Proof.
Let be an indivisible point set for some point p in an interval
of the real numbers. Suppose, on the contrary, that P is in motion. Then, initially P covers a subinterval I of
such that
(m is a Lebesgue measure). Since
is an indivisible point set,
. Therefore,
. The implication says
. If p is made to change position over
, we have
. By the additive property of length l, we have
. This contradicts the fact that
. It follows that p can never change position over
. Therefore, P cannot move.
3. Results
3.1. Analysis of the paradox
Before we go any further, we would like to point out the kind of information the paradox contains: for they will provide a setting toward logical understanding of the description, reasoning, and justification of the weakness behind its formulation. From the paradox, we have the following.
The initial head start given to the Tortoise is unspecified.
There is the “quicker” runner, Achilles, and the “slower” runner, the Tortoise.
The speeds of both runners are not particularly specified.
The lead established by the Tortoise in its first movement is not specified.
The race is divided into a number of smaller movements since the argument says that the fastest must first reach the point where the slowest started.
These information are given in generalities. Our reasoning, if it is to go to the heart of the paradox, must proceed in generalities as well.
For the sake of uniformity and clarity, the meaning of a physical task in this paper is the one given in the definition 3.1.1 below.
Definition 3.1.1.
A physical task is an act that has a definite beginning and a definite ending.
Remark.
Since the race is divided into sub-movements, then
The first movement, second movement, third movement, …for Achilles will, respectively, mean his travel from A0 to T0, from T0 to T1, from T1 to T2, and so forth.
For Tortoise; its nth movement means its travel from
to Tn for
(see Figure ).
To analyze the argument and point out the logical flaw it conceals, we will begin by accepting and following Zeno’s argumentation. However, we want to make it clear about our position that we do not think that assuming this way is in any way correct, but we do so in order to show how contradictory it is to assume this way.
Now, consider the racetrack (Figure 2) below ;
Let
A0 be the initial position of Achilles before the race begins
T0 be the position of the Tortoise at the beginning, and
Tn denote the nth lead position established by the Tortoise in the same amount of time used by Achilles in reaching
for all
.
When the whistle is blown, both runners will start running for a win. In the first movement, Achilles will spend a certain amount of time t1 to cover the distance . In the same amount of time t1, the Tortoise would have gone further ahead, to a new position T1. Since Achilles is quicker, then the distance
covered by Achilles must be strictly greater than the distance
covered by the Tortoise (Definition 2.1(iii)); for if
, Achilles would have covered equal or smaller distance than that covered by the Tortoise in equal amount of time. In this way, either both will have equal speeds, or Achilles’ speed will be less than the Tortoise speed. In both cases, Achilles will be quicker no longer. Thus, for Achilles to maintain his character of a quicker runner,
. Notice that
can gradually become very close, but must be strictly less than
. Thus, in the first movement, we notice that the time used by Achilles in reaching T0 from A0 determines the lead established by the Tortoise in reaching T1 from T0.
When the second movement is started, Achilles’ new position is at T0 and that of Tortoise is at T1. Now, Achilles is called to cover the distance that the Tortoise covered in the same amount of time t1 used by Achilles to move from A0 to T0. For Achilles to be quicker, he must cover this same distance
in the amount of time t2 less than the time t1 used by the Tortoise to cover the same distance (Definition 2.1(ii)). If Achilles spends more time covering
than the time used by the Tortoise, then Achilles ceases to be quicker, and the same holds if he spends the same amount of time as that used by the Tortoise to cover the same distance. At the end of the second movement, we observe that the distance
and
. While Achilles uses this less time t2 to cover
, the Tortoise, at the same time t2 will be adding another new distance
. Achilles will have to cover this distance again. If
, then the two runners will cover the same distance in the same reduced time t2, hence no one is quicker. If
, then Achilles is no longer the quicker but the Tortoise. But if
, then Achilles is quicker than the Tortoise.
Analysis of the second movement shows that the distance covered by the Tortoise in the first movement determines the time t2 Achilles will take to cover this distance in his second movement to maintain his character of being quicker. There is a change of conditions from the first to second movement; for in the first movement, the time t1 used by Achilles to cover the distance
determined the first lead
established by the Tortoise.
The conditions in the second movement hold for the next movements. The lead established by the Tortoise in the second movement determines the time that will be taken by Achilles to cover such distance in the third movement, and then, such time taken by Achilles determines the lead the Tortoise will cover in that third movement, and so on forever.
To sum up our analysis, we observe that it is justified that the leads established and times used to cover such leads are reduced from first to second movement, second to third movement and so on forever. All times and leads approach to but zero at far away. Moreover, we observe that after the first movement, the conditions of the argument change completely. The time taken by Achilles to cover the lead in the second and the rest movements is now determined by the lead established by the Tortoise, and this time is then used to determine the next lead. Achilles is then called to cover such leads. This makes the Tortoise to be always ahead at any instant and, according to Zeno, it can never be overtaken. This is the heart of the paradox and we claim that this conclusion is wrong. We will now show the weakness in the formulation and argumentation of the paradox.
3.2. The logical flaw of Achilles - Tortoise paradox
According to the analysis above, there are two respective sequences and
of leads and times for Achilles that each strictly decreases monotonically to but zero. It will reach a point on the racetrack where such distances (points) will be very close to each other such that they cannot be located on the racetrack (denseness of reals). At this point, Achilles can never take another step nor uplift his foot.
There is no justification from the argument itself or elsewhere that such sequence of leads follows geometric progression as the most celebrated Standard Mathematical Solution postulates. Therefore, it is generally not guaranteed that the convergence of the series
exists. Even if it does, as presented by Watling (Citation1953); Taylor (Citation1952), Whitehead (Citation1929: 69), and others who support the Standard Solution, it does not help to say that Achilles has succeeded in covering separately all such infinite diminishing distances. Because saying so is equivalent to admitting that Achilles has completed an infinite number of tasks in finite time. This is practically impossible.
Now; the flaw committed in logic is the use of the word must in the argument. This word must is divisive and ruling in the sense that it divides the racetrack into an infinite number of small movements and rules Achilles to stop and start at every position the Tortoise was as per Zeno’s instructions because the argument says … the pursuer must first reach the point whence the pursued started… There is no problem with the first movement. The flaw in logic appears in the second movement and is passed on to the next movements all the way to the end of the argument because Achilles is made to depend on the lead established by the Tortoise in the previous movement in determining the time he will spend to move such same lead and continue to be quicker. Achilles acts only if Tortoise does. As long as the pursued does not stop marching, it will never be overtaken. The earlier prohibition nullifies the existence of a race. This contradicts the argument itself, since it assumes that there is a race.
There is also a quest of how small in size the runners’ surfaces in contact with the racetrack should be if Zeno’s instructions are to be followed and effected. The leads established by the Tortoise decrease monotonically as the process continues. If Achilles is lucky enough to cover all such infinite number of leads one by one, then his surface (or step-size) in contact with the racetrack at far away would be required to be too small to fit into every segment. But there is no such positive size that is so small that any other size would be larger (Theorem 2.1). It follows that Achilles’s step-size cannot be made to be the smallest so that any other positive distance would be greater. Whatever small Achilles’s step-size is, there is always another size that is smaller than his. It follows that Achilles cannot complete such an infinite number of leads one by one. Therefore, the conclusion of the standard solution that the series
gives a finite sum makes no metaphysical sense in explaining this consequence.
We thus dismiss the word must in Zeno’s argument: for it divides the whole movement into smaller infinite numbers of movements that condition Achilles to traverse them one by one. Such a dismissal allows Achilles to race independent of the leads established and times used by Tortoise. In this way, the Tortoise will be overtaken easily.
3.3. Solution to the paradox: Analysis and topological approaches
We now present the solution to Achilles-Tortoise paradox. We show that such a sequence of leads will be covered by Achilles in a finite number of Achilles’ steps in a finite amount of time in the absence of the word must. The mathematical rule which the leads follow; whether geometric, arithmetic, or harmonic, does not matter. They will be covered anyway. The solution we provide assumes the following theses:
Thesis of Existence and motion: This states that which exists has size and thickness and a point or that without parts cannot be in motion of itself (Theorem 2.3).
Achilles and Tortoise have a definite size. This size remains unchanged throughout the course of the race. At any instant, their surface part that is in contact with the space is a linear continuum of length (or size) equal to the size of their contacting surfaces. This postulates that motion occurs in the form of non-degenerate intervals rather than points. This together with assertion
is a consequence of Theorem 2.3 and 2.1.
Topological approaches, mainly of open balls and convergence, from the standard topological space
come into play. This is in line with the thesis
. Since nothing indivisible moves, then self-motion is for that with size and thickness. This equates to claiming that motion occurs in intervals.
For illustrative purposes, the centre of mass of a runner will represent the position of a runner at any time. Consider the below.
Let
A0= Initial position of Achilles,
T0= Initial position of the Tortoise,
Tn= New position of Tortoise reached at the same amount of time that Achilles took to reach for
,
d1= Initial distance from A0 to T0 separating the two runners (Initial head start given to the Tortoise),
dn= The distance from to
for
Since the sequence consists of strictly non-overlapping monotonic decreasing distances dn such that
for all
, then it follows that such a sequence is bounded below.
By Theorem (2.2), the sequence is convergent in the Standard Euclidean Metric Space
and
Notice that , but that is not the case. By definition of convergence of sequence of reals, EquationEquation 1
(1)
(1) implies that for any positive real number ϵ, there exists a natural number
depending on the choice of ϵ such that
The secret lies in this definition given in EquationEquation 2.(2)
(2) Here is where Achilles’ call to perform an infinite number of steps is dismissed. What does ϵ represent in our solution? This is the step-size of Achilles (refer theses T1 and T2 above) since it is the one which executes the job.
Now, let ϵ be a step-size of Achilles (or anyone who assumes Achilles’ character in the race). Since Achilles is known, so is ϵ. Therefore, we find such that EquationEquation (2)
(2)
(2) holds.
Under standard topology in topological space , EquationEquation (2)
(2)
(2) simply says that for any step-size ϵ > 0, there is an open ball
centered at 0 with radius ϵ > 0 such that
for all
for some natural number
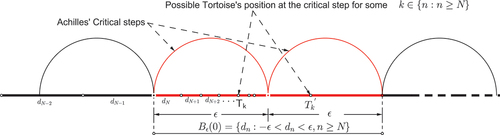
. Since dn are collinear, it follows that the line segment (Figure ) containing all the infinite number of finite distances
is wholly contained in the open ball
for all
(see Figure ).
Therefore, for all ,
. This explains the uniqueness of our solution from the standard solution (see critique
of the standard solution in Subsection 1.2 in this work). Achilles’ step-size ϵ forms an open ball
which eventually covers infinitely many distances without Achilles having to traverse them separately. Achilles, as a physical point at any time, occupies a space that is infinitely divisible into infinitely many segments, of which Achilles does not need to go through such segments separately to cover
in the absence of the word must in the paradox, only 2ϵ does the job. The first N − 1 finite distances
have a finite sum
. Let
. Achilles will need a maximum number of
steps to cover the distance . So to overtake the Tortoise, Achilles will have to run a maximum of z + 1 steps only if
. At this time, the Tortoise will be at the point Tk (see Figure ). If
, Achilles will run a maximum of z+2 steps to overtake the Tortoise which, at this time, will be at the point
(see Figure ).
The open ball in Figure is the critical region which contains the overtaking step. By critical region; we mean the region (interval) which contains the last step, which we call it the critical step, taken by Achilles to win the race. This proves that the final step exists. Therefore, Achilles does not need to take infinite number of steps to overtake the Tortoise, so the claim that he has got no enough time due to the presence of too many steps he has to take, as Zeno and Modern Eleatics claim, is the false claim.
Example 3.3.1.
Suppose that Achilles and Tortoise race at constant speeds (constant speeds generate a geometric sequence of leads) of 1m/s and m/s, respectively, and let 1km be the initial head start given to the Tortoise. By following Zeno’s instructions, we have the infinite sequence
of leads (see Figure ).
We want to be understood, as we have shown that Achilles does not go through such distances separately one by one by making stops and starts at every point the Tortoise was; but we aim to use such a false description to show that they can be covered in a finite number of steps when Achilles is allowed to race independently.
Now, from our example, we have a strictly monotonic decreasing sequence of non-overlapping leads (in km). Since
for all
, then the given sequence is bounded below and by Theorem (2.2),
is convergent in
under standard topology and
Equation implies that for any positive real number ϵ, there exists a natural number
(which depends on the choice of ϵ) such that
Let ϵ be given, then equation gives
Since we need to choose in such a way that
holds for all
, then from equation
we choose
Since ϵ is the Achilles step-size and we know who Achilles is, the exact value of ϵ is known. Let km. Equation
gives
. Thus for ϵ = 0.0005 km and from equation
we have that
for all
. Since
are collinear, the entire line segment containing such distances is contained entirely in the open interval
for all
and thus
. Achilles will cover the distance
in a total of steps and will need
steps to cover the remaining distances . To overtake the Tortoise, Achilles will have to run a maximum number of 3001 steps; a distance of 1.5005 km in approximately 25.008 minutes. This time is in agreement with the time
obtained by usual methods. The error in time from the two approaches is due to the approximations and truncations in EquationEquation (8)(8)
(8) and (Equation9
(9)
(9) ). At the 3000th Achilles’ step, the two will be approximately at the dead level, and at the end of Achilles’ 3001th step, the Tortoise is some distance behind Achilles. At this step, the situation changes completely. The quicker runner holds a lead and will always be ahead of the slower, and the sequence of leads will begin to increase monotonically without bound should the race be continued.
4. Discussion
The results from analysis of the paradox show, similarly to other readings, according to Zeno’s instructions, that the infinite sequence of leads decreases monotonically. However, there is no mention of the cause of such an infinite sequence, even in readings like Black (Citation1951) and Thomson (Citation1954), which contribute in refuting Zeno’s conclusion. According to our analysis, we observe that the word must in the argument makes Achilles make frequent stops and starts at each point the Tortoise was. This is the source of such infinite sequence of leads, the difficulty which the quickest is called to complete.
The investigation of the logical flaw of the argument shows that the requirement of the quickest to perform an infinite number of runs to overtake the slowest is due to the use of the word must. This word eliminates the freedom of Achilles to race but makes him dependent on the non-terminating leads established by the Tortoise. If this word is removed, the difficulties vanish. It is wrong to say that the Tortoise is never overtaken because it is always in front. However, to portray that the fallacy in Zeno’s argument is due to, as Black (Citation1951: 92) claims, the use of the words never and always does not follow. To refute the paradox, we must show that either the premise is false or the inference is invalid. Black did not elaborate how these two words refute the paradox (Wisdom, Citation1952: 68). The main source of those two words; never and always, according to our results, arise due to the implication of the word must, which Black did not explain nor mention as a cause.
Quan (Citation1963: 480) claims that Zeno has been correct all along, and any attempt to refute it must be wrong (Quan, Citation1963: 481). Then he comes back on his words. He uses the words Achilles cannot overtake the Tortoise because Zeno separates the runners at the start of the race as, to what he called, the genuine refutation of Zeno’s position, the position he claimed to be correct. So, according to his own reasons, he is wrong. He further in his solution ignores, without justification, Zeno’s instructions, which he defended to be correct. Then his solution betrays his own reasoning.
For the sake of brevity, the word must in the argument invalidates the inference in the sense that it is false to suppose that Achilles can traverse one by one such an infinite number of decreasing distances, because if he does, then his size would be too small that any other size would be larger. This is impossible (Theorem 2.1). Achilles cannot be considered as a mathematical point either (this is in agreement with Wisdom (Citation1952: 72)), because such a point has no self motion (Theorem 2.3). The same word must makes Achilles’ motion dependent on Tortoise’s. This violates the conditions of a race, where each competitor is given the freedom to run. The later implies that the argument itself is false. Therefore, to eliminate the necessity of Achilles in performing an infinite number of runs, the word must in the argument should disappear. Its disappearance consequently annihilates the dilemma of the paradox, and that absurd conclusion is no longer there.
After identifying and eliminating the illusive word must in the argument, the solution of Achilles overtaking Tortoise becomes easier. Then everyone can solve it. Our solution, built on basis of open balls, and convergence of sequences shows that only a finite number of runs are needed by Achilles to overtake the Tortoise. Our solution represents Achilles as a physical point, just as Wisdom (Citation1941, Citation1952). This is in contrast to the advocates of the Standard Solution who treat Achilles as a mathematical point (Euclid’s point). The difference between the two is that the former uses the theory of existence (Theses and
) and legitimizes motion, while the latter treats Achilles as a mathematical point and falls into the trap of Theorems 2.3 and 2.1. Unlike the Standard Solution, our solution does not give the exact mathematical point where the overtaking takes place, but gives, in the form of open balls (intervals), the exact step the overtaking takes place.
Although we have been able to refute Zeno’s Achilles-Tortoise paradox, we think that the main problem generally still exists concerning the concept of infinite in explaining physical processes. The question of the completion of an infinite sequence of physical tasks in finite time poses severe difficulties in mathematical analysis. The following are the concerns we would like to recommend for future work:
How can we demonstrate the completion of an infinite sequence of physical tasks? To make it clear, all physical processes are finite point sets having a definite beginning and a definite ending. Considering a case of fractal curves, for instance, the existence of an infinitely long mathematical object that encloses a finite area such as snowflake curve. Does this object really exist in the physical world? If it does, how is its construction completed then? The procedure that makes it relies on the limits of an infinite sequence of numbers generated by infinite cutting and gluing of the sides of an equilateral triangle (see Stewart (Citation2008: 761)). The sequence has no last term. If it does not exist, are we to accept the claim by Thomson (Citation1954); Russell (Citation1914); Black (Citation1951) and others that infinite is useless in explaining physical processes, and hence does not exist at all?
Another thing is concerning the smallest indivisible point that makes up a continuous entity. While refuting the standard solution, we arrived at a contradiction by treating Achilles as an indivisible point, or a line segment being the union of mathematical points. The question here is: what makes a distance? Is it the number of points on the line? If it is, then each line has zero length. If it is not, then what?, and what makes that what?
Acknowledgements
The authors acknowledge the technical assistance and every kind of unconditional cooperation from the two departments to which the authors belong. They also express their gratitude to the anonymous reviewers for their helpful suggestions, which helped to improve the quality of this paper.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Additional information
Funding
References
- Alba, P. G. (1996). Why mathematical solutions of Zeno’s paradoxes miss the point: Zeno’s one and many relation and Parmenides’ prohibition. Review of Metaphysics, 50(2), 299–314. https://doi.org/10.2307/20130032
- Barnes, J. (1991). The complete works of Aristotle: The revised oxford translation (Vol. 1). Princeton University Press.
- Bartle, R. G., & Sherbert, D. R. (2000). Introduction to real analysis (3rd ed.). John Wiley & Sons, Inc.
- Benacerraf, P. (1962). Tasks, super-tasks, and the modern eleatics. Journal of Philosophy, 59(24), 765–784. https://doi.org/10.2307/2023500
- Black, M. (1951). Achilles and the Tortoise. Analysis, 11(5), 91–101. https://doi.org/10.1093/analys/11.5.91
- Dowden, B. (2010). Zeno’s Paradoxes. In Internet encyclopaedia of philosophy. ISSN 2161-0002. https://iep.utm.edu/
- Grünbaum, A. (1967). Modern science and Zeno’s paradoxes. Wesleyan University Press.
- Quan, S. (1963). The solution of the achilles paradox. Review of Metaphysics, 16(3), 473–485.
- Russell, B. (1914). Our knowledge of the external world as a field for scientific method in philosophy. Open Court Publishing Co.
- Salmon, W. C. (1970). Zeno’s Paradoxes. The Bobbs-Merrill Company Inc.
- Shamsi, F. A. (1972). Zeno’S paradoxes: Towards a solution at last. Islamic Studies, 11(2), 125–151.
- Simplicius (a). (1995). On Aristotle’s physics: In readings in ancient Greek philosophy from Thales to Aristotle (S. M. Cohen, P. Curd and C. D. C. Reeve, Eds.). Hackett Publishing Co. Inc.
- Stewart, J. (2008). Calculus: Early transcendentals (6th ed.). Thomson Learning, Inc.
- Taylor, R. (1952). Mr. Black on temporal paradox. Analysis, 12(2), 38–44. https://doi.org/10.1093/analys/12.2.38
- Thomson, J. (1954). Tasks and Super-Tasks. Analysis, 15(1), 1–13. https://doi.org/10.1093/analys/15.1.1
- Watling, J. (1953). The sum of an infinite series. Analysis, 13(2), 39–46. https://doi.org/10.1093/analys/13.2.39
- Weyl, H. (1949). Philosophy of mathematics and natural science. Princeton University Press.
- Whitehead, A. N. (1929). Process and reality. Macmillan Publishing Co., Inc.
- Wisdom, J. O.(1941). Why Achilles does not fail to catch the tortoise. Mind, New Series, 50(197), 58–73. https://doi.org/10.2307/2250498
- Wisdom, J. O. (1952). Achilles on a physical racecourse. Analysis, 12(3), 67–72. https://doi.org/10.1093/analys/12.3.67