Numerical modeling on age-based study of coronavirus transmission

ABSTRACT

Ethiopia is one of the countries highly affected by the COVID-19 pandemic in Africa. A new study has looked at the transmission dynamics of the outbreak in Ethiopia based on the age categories of the infected individuals. Infected individuals are divided into three age categories (less than 14 years (I${}_1$), 15–54 years (I${}_2$), and above 54 years I${}_3$). Chebyshev polynomial of the fourth kind is used to convert a fractional system into an algebraic system of equations, which is then solved using iterative methods. The fundamental reproduction number $({\mathcal{R}}_0)$ is calculated using the next-generation matrix technique, and the disease-free and endemic equilibrium points, as well as their stability, are carefully studied. We calculated the parameters and starting conditions provided for our model using data from the Ethiopian Public Health Institute (EPHI) and the Ethiopian Ministry of Health from 29 February 2021, to 7 June 2021.

KEYWORDS:

• COVID-19
• Mittag-Leffler function
• caputo fractional derivative
• Chebyshev polynomials
• fractional modeling
• stability analysis
• Chebyshev spectral collocation method

MATHEMATICS SUBJECT CLASSIFICATIONS:

• 92-10
• 33F05
• 65L60

1. Introduction and preliminary

Currently, Coronavirus disease 2019 (COVID-19) is a world health problem that has affected and killed millions of people. In December 2019, Wuhan, China, marked the beginning of a new Coronavirus outbreak [1, 2]. On March 11, 2020, the World Health Organization (WHO) named the disease a pandemic [3]. The most frequent symptoms are fever, dry cough, and shortness of breath, or trouble breathing. Symptoms include muscle and joint pain, headaches, sore throats, and a lack of taste or smell. To minimize this deadly disease from spreading further, social distance, face mask, washing hands frequently, minimizing non-essential trips, case isolation, family quarantine, and college and university closure are all being done [4–9].

The Ethiopian Federal Ministry of Health (MOHE) and the Ethiopian Public Health Institute (EPHI) reported the first case of Covid-19 in Addis Ababa on March 13, 2020. The first case was a 48-year-old Japanese man who traveled from Japan to Burkina Faso before arriving in Addis Ababa [10]. According to MOHE and EPHI's public health recommendations, anyone could be the next person to acquire COVID-19, but we can prevent it if we act immediately. We must use all COVID-19 intervention techniques to stay alive and well. Older people and those with pre-existing medical conditions (such as cardiovascular disease, chronic respiratory disease, or diabetes) are at high risk for severe disease.

In Ethiopia, there were 272, 914 confirmed COVID-19 cases and 4209 deaths as of June 6, 2021. This puts Ethiopia in fourth place in Africa in terms of confirmed cases and fifth place in terms of deaths caused by COVID-19. This week, there was a 27% decrease in the number of COVID-19 confirmed cases (for the ninth consecutive week), and there was a 32% decrease in the number of deaths due to COVID-19. The number of COVID-19 confirmed cases, deaths due to COVID-19, and laboratory tests and positivity rate in Ethiopia have shown a decrement in the last consecutive weeks [11]. Habenom et al. [12, 13] developed a fractionalized mathematical model for the Covid-19 epidemic's transmission in Ethiopia, which also helps analyse the Covid virus's behaviour.

In outbreak investigations, mathematical modeling is often utilized to understand the processes of infectious disease transmission and to interpret trends in epidemiological data [14]. Agarwal et al. [15] developed a mathematical model for transmission analysis based on the infection dynamics of the pandemic COVID-19. In which the basic reproduction number and balance points are calculated from the model to assess the transmittance of COVID-19. According to medical reports, both dengue and covid-19 have similar symptoms in the early stages. The transmission dynamics of both lethal viruses have been evaluated and predicted in co-infection modeling [16].

Mathematical modeling has become a key tool in assessing the spread and management of infectious diseases, taking into consideration essential variables that influence disease progression, such as transmission and recovery rates. Models based on mathematics can be used to predict how the disease will spread over time [17–19]. Based on the conservation principle of population dynamics, suitable mathematical models for COVID-19 pandemic outbreaks have been established [20–22]. In [23], to extend the Covid-19 model, a set of real-world data was used by taking into account the isolation and quarantine. Chowdhury et al. [24] have analysed the interaction between the immune system and SARS-CoV-2 within the host. And also, Chowdhury et al. [25] gave a mathematical model that deals with the asymptomatic and symptomatic disease transmission process in the COVID-19 outbreak. There has been a lot of interest in using mathematical models and simulations to explore the dynamics of infectious diseases in recent years [26], because they help us better understand how diseases spread and provide a better understanding of epidemiological data. Essential parameters that may have a high influence on the outbreak rate and control strategies of Coronavirus disease 2019 are seen.

In a different way, Mahmoudi et al. [27] studied the spread of COVID-19 in the United States, Spain, Italy, the United Kingdom, Germany, France, and Iran using the fuzzy clustering technique. Simultaneously, Din et al. [28] investigated the stationary distribution of the pandemic COVID-19 and the extinction of the disease using stochastic methods. The computation of derivatives or integrals of any positive real order is considered as fractional calculus. Fractional calculus has attracted the interest of many researchers in different areas, including mathematics, physics, chemistry, biology, engineering, and even finance and social science, in recent years [29–32]. In this paper, we investigated a mathematical model for COVID-19 that might be used to investigate Coronavirus transmission dynamics in Ethiopia based on the age categories of infected people. The dynamical transmission mechanism of the new Coronavirus is studied using Caputo fractional derivative.

The Mittag-Leffler (M-L) function, the fractional derivative, and a few key Chebyshev polynomial of the fourth type characteristics are covered in this section.

1.1. The Mittag-Leffler function

The one-parameter and two-parameter representations of the M-L function in terms of a power series are as follow [33]: (1) $E_{\psi }(u)=\sum _{m=0}^{\mathrm{\infty }}{\displaystyle \frac{u^m}{\mathrm{\Gamma }(\psi m+1)}},\psi >0,$(1) and (2) $E_{\psi ,\mu }(u)=\sum _{m=0}^{\mathrm{\infty }}{\displaystyle \frac{u^m}{\mathrm{\Gamma }(\psi m+\mu )}},\psi >0,\mu >0.$(2) where the function $\mathrm{\Gamma }(u)$, commonly referred to as Euler's integral, is defined as (3) $\mathrm{\Gamma }\left(u\right)={\int }_0^{\mathrm{\infty }}{w}^{u-1}{e}^{-w}\mathrm{d}w,u>0$(3) From Ref. [34], the Laplace transform of the function $t^{\mu -1}{E}_{\psi ,\mu }(\eta t^{\psi })$ is (4) $\mathcal{L}[t^{\mu -1}{E}_{\psi ,\mu }(\eta t^{\psi })]=\{\begin{array}{l}{\displaystyle \frac{s^{\psi -\mu }}{s^{\psi }+\eta }},\eta <0,\\ \\ {\displaystyle \frac{s^{\psi -\mu }}{s^{\psi }-r}},\eta >0,\end{array}$(4)

1.2. Caputo fractional derivative

The fractional derivative of order δ in Caputo sense is defined in the following form Refs. [35–37] (5) $D^{\delta }y(t)={\displaystyle \frac{1}{\mathrm{\Gamma }(n-\delta )}}{\int }_0^t{\displaystyle \frac{d^{n}y}{\mathrm{d}{\xi }^n}}{(t-\xi )}^{n-1-\delta }\mathrm{d}\xi ,\delta \in (n-1,n],n\in \mathbb{N}.$(5) For Caputo fractional derivative, we have (6) $\begin{array}{rl}& D^{\delta }y(t)=0,(y\mathrm{is}\mathrm{a}\mathrm{constant})\end{array}$(6) (7) $\begin{array}{rl}& D^{\delta }{t}^n=\{\begin{array}{ll}0,& \mathrm{for}n\in {\mathbb{N}}_0\mathrm{and}n<\lceil \delta \rceil .\\ {\displaystyle \frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+1-\delta )}}{t}^{n-\delta },& \mathrm{for}n\in {\mathbb{N}}_0\mathrm{and}n\ge \lceil \delta \rceil .\end{array}\end{array}$(7) where ${\mathbb{N}}_0=\{0,1,2,\dots \}$ and $\lceil \delta \rceil$ denote the smallest integer greater than or equal to δ.

The Laplace transform of $D^{\delta }y(t)$ is given by: (8) $\mathcal{L}\{D^{\delta }y(t)\}=s^{\delta }Y\left(s\right)-\sum _{k=0}^{n-1}{s}^{\delta -k-1}{y}^{(k)}\left(0\right),\delta \in (n-1,n],n\in \mathbb{N}.$(8) with $Y(s)$ is the Laplace transform of $y(t)$.

1.3. Chebyshev polynomials of the fourth kind

On the interval $x\in [-1,1]$, Chebyshev polynomials of fourth kind $W_n(x)$ can be generated using the following recurrence relation [38]: (9) $W_{n+1}(x)=2x{W}_n(x)-W_{n-1}(x),n=1,2,\dots$(9) with starting polynomials $W_0(x)=1,\mathrm{and}{W}_1(x)=2x+1$. Applying these polynomials on the interval $t\in [0,1]$, we have the so-called shifted Chebyshev polynomials (SCP) of the fourth kind with the change of variable x = 2t−1. Let the SCP of the fourth kind $W{}_n(2t-1)$ is denoted by $W_n^{\ast }(t)$ and it can be obtained as follows: (10) $W_{n+1}^{\ast }(t)=2(2t-1)W_n^{\ast }(t)-W_{n-1}^{\ast }(t),n=1,2,\dots$(10) where $W_0^{\ast }(t)=1,W_1^{\ast }(t)=4t-1$. The analytic form of $W_n^{\ast }(t)$ of degree n is given by: (11) $W_n^{\ast }(t)=\sum _{i=0}^n(-1{)}^i(2{)}^{2n-2i}{\displaystyle \frac{\mathrm{\Gamma }(2n-i+1)}{\mathrm{\Gamma }(i+1)\mathrm{\Gamma }(2n-2i+1)}}{t}^{n-i}n=1,2,\dots$(11) A function $g(t)$, square-integrable on $[0,1],$ is represented by an infinite expansion of $W_n^{\ast }(t)$ as (12) $g(t)=\sum _{i=0}^{\mathrm{\infty }}{b}_i{W}_i^{\ast }(t)$(12) The coefficients $b_i$ are given by (13) $b_i=(2i+1){\int }_0^{1}g(t)W_i^{\ast }(t)\mathrm{d}t,i=1,2,\dots$(13) The first $(n+1)$ -- terms of shifted Chebyshev polynomials of the fourth kind are considered. Then we have (14) $g_n(t)=\sum _{i=0}^n{b}_i{W}_i^{\ast }(t)$(14) For suitable SCP of the fourth kind collocation method, we have to collocate Equation (14(14) $g_n(t)=\sum _{i=0}^n{b}_i{W}_i^{\ast }(t)$(14) ) at $n+1-\lceil \alpha \rceil$ shifted Chebyshev fourth kind roots $t_p,p=0,1,..,n-\lceil \alpha \rceil$.

Lemma 1.1

Let $g_n(t)$ be a function approximated in terms of the SCP fourth type provided in Equation (14(14) $g_n(t)=\sum _{i=0}^n{b}_i{W}_i^{\ast }(t)$(14) ), and suppose $\alpha >0$, then (15) $D^{\alpha }{g}_n\left(t\right)\approx \sum _{i=\lceil \alpha \rceil }^n\sum _{k=\lceil \alpha \rceil }^i{c}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }$(15)

where $\gamma {}_{i,k}^{(\alpha )}$ is given by (16) ${\gamma }_{i,k}^{(\alpha )}=(-1{)}^k{2}^{(2i-2k)}{\displaystyle \frac{\mathrm{\Gamma }(2i-k+1)\mathrm{\Gamma }(i-k+1)}{\mathrm{\Gamma }(k+1)\mathrm{\Gamma }(2i-2k+2)\mathrm{\Gamma }(i-k+1-\alpha )}}$(16)

2. Material and methods

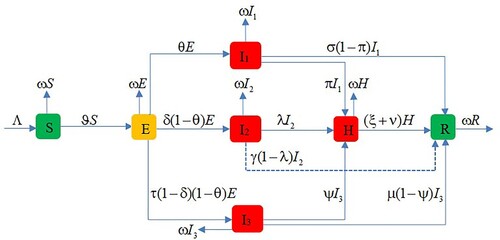
The majority of confirmed cases admitted to treatment centres in Ethiopia were between the ages of 15 and 54, with the majority of COVID-19-related deaths occurring in those over 64 years old, according to reported cases. This means that as the patient gets older, the chances of dying from COVID-19 increase. We divide the total population of Ethiopia into seven different classes named as susceptible (S), exposed (E), and infected people are divided into three age groups (i.e. less than 14 years (I${}_1$), 15–54 years (I${}_2$), and above 54 years (I${}_3$), hospitalized (H), and recovered and removed (R). The total population at any time t is given by (17) $N(t)=S(t)+E(t)+I_1(t)+I_2(t)+I_3(t)+H(t)+R(t).$(17) Individuals who have been recruited are assumed to be susceptible to a constant recruitment rate of Λ. Susceptible individuals get infected by infectious individuals with the force of infection $\vartheta ={\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon I_2+\varpi I_3)}{N}}$ (Figure 1).

Figure 1. Flow diagram of the SEI${}_1$I${}_2$I${}_3$HR model.

Figure 2. Confirmed cases and recovered cases from 29 February 2021 to 7 June 2021, in Ethiopia.

Figure 3. Testes performed and death cases from 29 February 2021 to 7 June 2021, in Ethiopia.

In the Caputo sense, the above model can be expressed as a system of fractional-order differential equations: (18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) where, $\vartheta ={\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon I_2+\varpi I_3)}{N}}$ with positive starting conditions (19) $S(0),E(0),I_1(0),I_2(0),I_3(0),H(0),R(0).$(19) The parameter Λ is the recruitment rate, ω is the natural death rate, ℵ is the rate of transmission (or contact rate), ε is the modification factor for infected class I${}_2$, ϖ is the modification factor for infected class I${}_3$, θ is the rate of the exposed population joining the infected class I${}_1$, δ is the rate of the exposed population joining infected class I${}_2$, and τ is the rate of joining the infected class I${}_3$ from the exposed The parameters π, λ, and ψ are rates at which infected individuals from I${}_1$, I${}_2$, and I${}_3$ are in hospital (or treatment centre). σ, γ, and µ are recovery rates from I${}_1$, I${}_2$, and I${}_3$. ξ is the rate at which hospitalized individuals are recovered and ν is COVID-19-induced death rate. Because model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) monitors the dynamics of the human population during the COVID-19 pandemic period, all the parameters are assumed to be non-negative.

2.1. Existence and uniqueness of solutions of SEI${}_1$I${}_2$I${}_3$HR model

One of the most important fields in the theory of fractional-order differential equations is the theory of solution existence and uniqueness [34, 39] and the references therein for some of the recent growth. Using the fixed point theorem [40], we will discuss the existence and uniqueness of solutions to the proposed model in this section. We simplify the proposed model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) in the following setting: (20) $\begin{array}{l}{D}^{\alpha }S(t)={\mathrm{\Theta }}_1(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }E(t)={\mathrm{\Theta }}_2(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_1(t)={\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_2(t)={\mathrm{\Theta }}_4(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_3(t)={\mathrm{\Theta }}_5(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }H(t)={\mathrm{\Theta }}_6(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }R(t)={\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R),\end{array}\}.$(20) where (21) $\begin{array}{l}{\mathrm{\Theta }}_1(t,S,E,I_1,I_2,I_3,H,R)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ {\mathrm{\Theta }}_2(t,S,E,I_1,I_2,I_3,H,R)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ {\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ {\mathrm{\Theta }}_4(t,S,E,I_1,I_2,I_3,H,R)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ {\mathrm{\Theta }}_5(t,S,E,I_1,I_2,I_3,H,R)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ {\mathrm{\Theta }}_6(t,S,E,I_1,I_2,I_3,H,R)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ {\mathrm{\Theta }}_7(t,S,E,I_1,I_2,I_3,H,R)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2\\ +\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(21) Thus, the proposed model (20(20) $\begin{array}{l}{D}^{\alpha }S(t)={\mathrm{\Theta }}_1(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }E(t)={\mathrm{\Theta }}_2(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_1(t)={\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_2(t)={\mathrm{\Theta }}_4(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }{I}_3(t)={\mathrm{\Theta }}_5(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }H(t)={\mathrm{\Theta }}_6(t,S,E,I_1,I_2,I_3,H,R),\\ D^{\alpha }R(t)={\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R),\end{array}\}.$(20) ) has the form (22) $\{\begin{array}{l}{D}^{\alpha }\mathrm{\Phi }(t)=\chi (t,\mathrm{\Phi }(t)),\\ \mathrm{\Phi }(0)={\mathrm{\Phi }}_0\ge 0\end{array}$(22) under the condition that (23) $\{\begin{array}{l}\mathrm{\Phi }(t)={(t,S,E,I_1,I_2,I_3,H,R)}^T,\\ \mathrm{\Phi }(0)={(S_0,E_0,I_1{}^0,I_2{}^0,I_3{}^0,H_0,R_0)}^T,\\ \chi (t,\mathrm{\Phi }(t))={\left({\mathrm{\Theta }}_i(t,S,E,I_1,I_2,I_3,H,R)\right)}^T,i=1,2,\dots ,7\end{array}$(23) Problem (22(22) $\{\begin{array}{l}{D}^{\alpha }\mathrm{\Phi }(t)=\chi (t,\mathrm{\Phi }(t)),\\ \mathrm{\Phi }(0)={\mathrm{\Phi }}_0\ge 0\end{array}$(22) ) which is equivalent to model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) has an integral representation is given by (24) $\mathrm{\Phi }(t)=\mathrm{\Phi }(0)+{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\chi (\xi ,\mathrm{\Phi }(t))(t-\xi {)}^{\alpha -1}\mathrm{d}\xi$(24) Let $\mathcal{B}=\mathbb{C}([0,a];\mathbb{R})$ stand for the Banach space of all continuous functions from $[0,a]$ to $\mathbb{R}$ with the norm defined by (25) ${\Vert \mathrm{\Phi }\Vert }_{\mathcal{B}}=\underset{t\in \mathcal{J}}{sup}|\mathrm{\Phi }(t)|,$(25) where $|\mathrm{\Phi }(t)|=|S(t)|+|E(t)|+|I_1(t)|+|I_2(t)|+|I_3(t)|+|H(t)|+|R(t)|$ and $S,E,I_1,I_2,I_3,H,R\in ([0,a],\mathbb{R})$.

Theorem 2.1

For every kernels ${\mathrm{\Theta }}_i,$ $i=1,2,\dots ,7$ in (21(21) $\begin{array}{l}{\mathrm{\Theta }}_1(t,S,E,I_1,I_2,I_3,H,R)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ {\mathrm{\Theta }}_2(t,S,E,I_1,I_2,I_3,H,R)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ {\mathrm{\Theta }}_3(t,S,E,I_1,I_2,I_3,H,R)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ {\mathrm{\Theta }}_4(t,S,E,I_1,I_2,I_3,H,R)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ {\mathrm{\Theta }}_5(t,S,E,I_1,I_2,I_3,H,R)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ {\mathrm{\Theta }}_6(t,S,E,I_1,I_2,I_3,H,R)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ {\mathrm{\Theta }}_7(t,S,E,I_1,I_2,I_3,H,R)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2\\ +\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(21) ), there exist ${\theta }_i,i=1,2,\dots ,7$ such that (26) $\Vert {\mathrm{\Theta }}_i(t,y)-{\mathrm{\Theta }}_i(t,y_1)\Vert \le {\theta }_i\Vert y(t)-y_1(t)\Vert$(26)

where y is the state vector presented as $\{S,E,I_1,I_2,I_3,H,R\}$ and are contractions for $0\le {\theta }_i<1,i=1,2,\dots ,7$

Proof.

For the state variable S, we have $\begin{array}{rl}& \Vert {\mathrm{\Theta }}_1(t,S)-{\mathrm{\Theta }}_1(t,S_1)\Vert =\Vert \mathrm{\Lambda }-(\vartheta +\omega )S-(\mathrm{\Lambda }-(\vartheta +\omega )S_1)\Vert \\ & \le {\theta }_1\Vert S_1-S\Vert \end{array}$ where ${\theta }_1={\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon i_2+\varpi I_3)}{N}}+\omega$, $\begin{array}{rl}\Vert S\Vert & =\underset{t\in \mathcal{J}}{sup}|S(t)|=n_6,\Vert E\Vert =\underset{t\in \mathcal{J}}{sup}|E(t)|=n_7,\Vert I_1\Vert =\underset{t\in \mathcal{J}}{sup}|I_1(t)|=n_1,\\ \Vert I_2\Vert & =\underset{t\in \mathcal{J}}{sup}|I_2(t)|=n_2\Vert I_3\Vert =\underset{t\in \mathcal{J}}{sup}|I_3(t)|=n_3,\Vert H\Vert =\underset{t\in \mathcal{J}}{sup}|H(t)|=n_4,\\ \Vert R\Vert & =\underset{t\in \mathcal{J}}{sup}|R(t)|=n_5.\end{array}$ It then follows that ${\mathrm{\Theta }}_1(t,S)$ satisfies the Lipschitz condition with Lipschitz constant

${\theta }_1={\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon I_2+\varpi I_3)}{N}}+\omega$. Moreover, if $0\le {\theta }_1<1$, then ${\mathrm{\Theta }}_1(t,S)$ is a contraction. In the same way, we can show the existence of Lipschitz constants ${\theta }_i,i=2,3,\dots ,7,$ and a contraction principle for ${\mathrm{\Theta }}_2(t,E),{\mathrm{\Theta }}_3(t,I_1),{\mathrm{\Theta }}_4(t,I_2),{\mathrm{\Theta }}_5(t,I_3),{\mathrm{\Theta }}_6(t,H),{\mathrm{\Theta }}_7(t,R)$. Now for $t=t_j,j=1,2,\dots ,$ defined the following recursive form of (24(24) $\mathrm{\Phi }(t)=\mathrm{\Phi }(0)+{\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\chi (\xi ,\mathrm{\Phi }(t))(t-\xi {)}^{\alpha -1}\mathrm{d}\xi$(24) ) (27) $y_j(t)-y_{j-1}(t)={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t{\mathrm{\Theta }}_i(\xi ,y_{j-1})(t-\xi {)}^{\alpha -1}\mathrm{d}\xi$(27) The difference between successive terms in the above equation and taking the norm on both sides of the resulting equation, we obtain: (28) $\Vert y_j(t)-y_{j-1}(t)\Vert ={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\Vert {\mathrm{\Theta }}_i(\xi ,y_{j-1})-{\mathrm{\Theta }}_i(\xi ,y_{j-2})\Vert |(t-\xi {)}^{\alpha -1}|\mathrm{d}\xi$(28) Furthermore, by taking y = S Equation (28(28) $\Vert y_j(t)-y_{j-1}(t)\Vert ={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\Vert {\mathrm{\Theta }}_i(\xi ,y_{j-1})-{\mathrm{\Theta }}_i(\xi ,y_{j-2})\Vert |(t-\xi {)}^{\alpha -1}|\mathrm{d}\xi$(28) ) can be reduced to the following expressions: $\begin{array}{rl}\Vert S_j(t)-S_{j-1}(t)\Vert & ={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\Vert {\mathrm{\Theta }}_i(\xi ,S_{j-1})-{\mathrm{\Theta }}_i(\xi ,S_{j-2})\Vert |(t-\xi {)}^{\alpha -1}|\mathrm{d}\xi \\ & \le {\theta }_1\Vert (S_{j-1}-S_{j-2})(t)\Vert \left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|.\end{array}$ As a result, we have (29) $\Vert S_j(t)-S_{j-1}(t)\Vert \le {\theta }_1\left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|\Vert S_{j-1}(t)-S_{j-2}(t)\Vert .$(29) The rest of the expressions can be reduced to the following form: (30) $\Vert y_{ij}(t)-y_{i(j-1)}(t)\Vert \le {\theta }_i\left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|\Vert y_{i(j-1)}(t)-y_{i(j-2)}(t)\Vert ,i=2,3,\dots ,7$(30)

Theorem 2.2

The Caputo fractional model given in (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) has a solution if we can find ℑ satisfying the inequality (31) ${\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}{\theta }_i<1,i=1,2,3,\dots ,7.$(31)

Proof.

From (29(29) $\Vert S_j(t)-S_{j-1}(t)\Vert \le {\theta }_1\left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|\Vert S_{j-1}(t)-S_{j-2}(t)\Vert .$(29) ) and (30(30) $\Vert y_{ij}(t)-y_{i(j-1)}(t)\Vert \le {\theta }_i\left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|\Vert y_{i(j-1)}(t)-y_{i(j-2)}(t)\Vert ,i=2,3,\dots ,7$(30) ) we have (32) $\Vert y_{ij}(t)\Vert \le \Vert y(0)\Vert {\left[{\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}{\theta }_i\right]}^n$(32) Theorem 2.1 confirmed the existence of solution, and we have to show that the functions $S(t),E(t),I_1(t),I_2(t),I_3(t),H(t),R(t)$ are solutions of model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ).

Let us assume that the following are satisfied: (33) $y(t)-y(0)=y_j(t)-d_{ij}(t)$(33) From (33(33) $y(t)-y(0)=y_j(t)-d_{ij}(t)$(33) ) we obtain (34) $\begin{array}{rl}\Vert d_{ij}(t)\Vert & ={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t\Vert {\mathrm{\Theta }}_i(\xi ,y_j)-{\mathrm{\Theta }}_i(\xi ,y_{j-1})\Vert |(t-\xi {)}^{\alpha -1}|\mathrm{d}\xi \\ & \le {\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}{\theta }_i\Vert y_j-y_{j-1}\Vert .\end{array}$(34) Recursively repeating the process results in (35) $\Vert d_{ij}(t)\Vert \le {\left[{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right]}^j{\theta }_i^j\Vert y_1-y_0\Vert ,$(35) Taking $t=\mathrm{\Im }$ yields (36) $\Vert d_{ij}(t)\Vert \le {\left[{\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right]}^j{\theta }_i^j\Vert y_1-y_0\Vert ,$(36) Applying the limit to both sides of (36(36) $\Vert d_{ij}(t)\Vert \le {\left[{\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right]}^j{\theta }_i^j\Vert y_1-y_0\Vert ,$(36) ) as $j\to \mathrm{\infty }$ we see that $\Vert d_{ij}(t)\Vert \to 0$ for ${\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}{\theta }_i<1.$ Theorems 2.1 and 2.2 guarantees the existence of the solution of model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) by the Banach fixed point theorem [41].

Theorem 2.3

uniqueness of solutions

The Caputo fractional model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) has a unique solution provided that (37) $\left|{\displaystyle \frac{{\mathrm{\Im }}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|{\theta }_i<1,i=2,3,\dots ,7.$(37)

Proof.

Let us assume that $S(t),E(t),I_1(t),I_2(t),I_3(t),H(t),R(t)$ are solutions to (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ). Then (38) $S(t)-S_1(t)={\displaystyle \frac{1}{\mathrm{\Gamma }(\alpha )}}{\int }_0^t({\mathrm{\Theta }}_1(\xi ,S)-{\mathrm{\Theta }}_1(\xi ,S_1))(t-\xi {)}^{\alpha -1}\mathrm{d}\xi$(38) Taking the norm of both sides, obtain (39) $\Vert S(t)-S_1(t)\Vert \le \left|{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right|{\theta }_1\Vert S-S_1\Vert .$(39) Since $1-{\theta }_1{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}>0,$ we obtain $\Vert S(t)-S_1(t)\Vert =0$. Thus, we have $S(t)=S_1(t)$.

In the same way, we can show that $E(t)=E_1(t),I_1(t)=I_1{}^{{}^{\prime }}(t),I_2(t)=I_2{}^{{}^{\prime }}(t),I_3(t)=I_3{}^{{}^{\prime }}(t),$

$H(t)=H_1(t),R(t)=R_1(t)$.

Lemma 2.1

The epidemiologically feasible region of model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) is given by (40) $\mathrm{\Theta }=\{S(t),E(t),I_1(t),I_2(t),I_3(t),H(t),R(t)\in {\mathbb{R}}_{+}^7:N\left(t\right)\le {\displaystyle \frac{\mathrm{\Lambda }}{\omega }}\}.$(40) with positive initial conditions in (19(19) $S(0),E(0),I_1(0),I_2(0),I_3(0),H(0),R(0).$(19) ) is a positive invariant for system (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ).

Proof.

Adding each equation in model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) yields the dynamics of the overall population, given by (41) $D^{\alpha }N(t)\le \mathrm{\Lambda }-\omega N$(41) Applying the Laplace transform on (41(41) $D^{\alpha }N(t)\le \mathrm{\Lambda }-\omega N$(41) ) and the idea of (4(4) $\mathcal{L}[t^{\mu -1}{E}_{\psi ,\mu }(\eta t^{\psi })]=\{\begin{array}{l}{\displaystyle \frac{s^{\psi -\mu }}{s^{\psi }+\eta }},\eta <0,\\ \\ {\displaystyle \frac{s^{\psi -\mu }}{s^{\psi }-r}},\eta >0,\end{array}$(4) ), we obtain: (42) $N\left(t\right)\le E_{\alpha ,1}(-\omega t^{\alpha })N(0)+{\displaystyle \frac{\mathrm{\Lambda }}{\omega }}(1-E_{\alpha ,1}(-\omega t^{\alpha })),$(42) Since, $0\le E_{\alpha ,1}(-\omega t^{\alpha })\le 1,$ we have $N(t)\le {\displaystyle \frac{\mathrm{\Lambda }}{\omega }}$ and hence, the region Θ is a positively invariant set for the system (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ).

Theorem 2.4

If the starting solutions satisfy $S(0)\ge 0,E(0)\ge 0,I_1(0)\ge 0,I_2(0)\ge 0,I_3(0)\ge 0,$ $H(0)\ge 0,R(0)\ge 0$, then the solutions $S(t),E(t),I_1(t),I_2(t),I_3(t),H(t)$, $R(t)$ of the system (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) are positive $\mathrm{\forall }t\ge 0$.

Proof.

Take the first equation of the COVID-19 model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) (43) $D^{a}S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S\ge -(\vartheta +\omega )S$(43) where $\vartheta ={\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon I_2+\varpi I_3)}{N}}+\omega$.

Following Lemma 2.1, $I_1+\epsilon I_2+\varpi I_3$ which is bounded by a constant ${\vartheta }_0$, we have (44) $D^{a}S(t)\ge -rS(t)$(44) where r is a constant equal to ${\displaystyle \frac{{\vartheta }_0}{N}}+\omega .$

Applying the Laplace transform in the previous inequality (44(44) $D^{a}S(t)\ge -rS(t)$(44) ), we arrive at (45) $S(t)\ge E_{\alpha ,1}(-r{t}^{\alpha })S(0).$(45) Since $E_{\alpha ,1}(-r{t}^{\alpha })>0$ and $S(0)\ge 0$, then the solution $S(t)$ is positive. Similarly, it can be shown that the quantities ($E(t),I_1(t)$, $I_2(t),I_3(t),H(t),R(t)$) are positive $\mathrm{\forall }t\ge 0$.

2.2. Stability analysis of SEI${}_1$I${}_2$I${}_3$HR model

The disease-free equilibrium corresponds to the case when there are no infections in the population. All the infectious compartments are set to zero. That is $E=I_1=I_2=I_3=H=0$. Also, setting the fractional derivatives of non-infectious compartments to zero in our model equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ). That is $D^{\alpha }S(t)=D^{\alpha }R(t)=0$. Hence, the disease-free equilibrium point ${\mathrm{\Psi }}_0$ is given by (46) ${\mathrm{\Psi }}_0=(S^0,E^0,I_1{}^0,I_2{}^0,I_3{}^0,H^0,R^0)=({\displaystyle \frac{\mathrm{\Lambda }}{\omega }},0,0,0,0,0,0).$(46) The matrix S at ${\mathrm{\Psi }}_0$ given by $S=\left[\begin{array}{ccccc}0& \mathrm{\aleph }& \epsilon \mathrm{\aleph }& \varpi \mathrm{\aleph }& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],$ and the matrix T at ${\mathrm{\Psi }}_0$ is $\begin{array}{rl}T& =\left[\begin{array}{ccccc}{a}_1& 0& 0& 0& 0\\ -\theta & a_2& 0& 0& 0\\ -\delta (1-\theta )& 0& a_3& 0& 0\\ -\tau (1-\delta )(1-\theta )& 0& 0& a_4& 0\\ 0& -\pi & -\lambda & -\psi & \xi +\nu +\omega \end{array}\right]\\ a_1& =\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega ,a_2=\pi +\sigma (1-\pi )+\omega ,\\ a_3& =\lambda +\gamma (1-\lambda )+\omega \\ a_4& =\psi +\mu (1-\psi )+\omega ,\end{array}$ Then, the largest eigenvalue of the next generation matrix $S{T}^{-1}$ is the required effective reproduction number which is given by (47) ${\mathcal{R}}_0={\displaystyle \frac{\mathrm{\aleph }\theta }{a_1{a}_2}}+{\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_1{a}_3}}+{\displaystyle \frac{\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_1{a}_4}}$(47) Three effective reproduction numbers are comprised in Equation (47(47) ${\mathcal{R}}_0={\displaystyle \frac{\mathrm{\aleph }\theta }{a_1{a}_2}}+{\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_1{a}_3}}+{\displaystyle \frac{\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_1{a}_4}}$(47) ). The first number is ${\mathcal{R}}_{0I_1}={\displaystyle \frac{\mathrm{\aleph }\theta }{a_1{a}_2}}$, it is defined as the number of new COVID-19 cases generated from the first age class of infected individuals (I${}_1$), the second number is ${\mathcal{R}}_{0I_2}={\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_1{a}_3}}$ defined as the number of cases generated from the second age class of infected individuals (I${}_2$) and the third number is ${\mathcal{R}}_{0I_3}={\displaystyle \frac{\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_1{a}_4}}$, and it defines the number of COVID-19 cases generated from the third-age class of infected individuals (I${}_3$). It can be written as a mathematical expression: (48) ${\mathcal{R}}_0={\mathcal{R}}_{0I_1}+{\mathcal{R}}_{0I_2}+{\mathcal{R}}_{0I_3}$(48)

Theorem 2.5

If ${\mathcal{R}}_0<1$, then the disease-free equilibrium point ${\mathrm{\Psi }}_0$ in Equation (46(46) ${\mathrm{\Psi }}_0=(S^0,E^0,I_1{}^0,I_2{}^0,I_3{}^0,H^0,R^0)=({\displaystyle \frac{\mathrm{\Lambda }}{\omega }},0,0,0,0,0,0).$(46) ) is locally asymptotically stable and unstable for ${\mathcal{R}}_0>1$.

Proof.

To assess the local stability of the disease-free equilibrium point, we investigate the behaviour of our model population near this equilibrium solution. At ${\mathrm{\Psi }}_0$, the Jacobian matrix of (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) is now: (49) $J_{{\mathrm{\Psi }}_0}=\left[\begin{array}{ccccccc}-\omega & 0& -\mathrm{\aleph }& -\epsilon \mathrm{\aleph }& -\varpi \mathrm{\aleph }& 0& 0\\ 0& -a_1& \mathrm{\aleph }& \epsilon \mathrm{\aleph }& \varpi \mathrm{\aleph }& 0& 0\\ 0& \theta & -a_2& 0& 0& 0& 0\\ 0& \delta (1-\theta )& 0& -a_3& 0& 0& 0\\ 0& \tau (1-\delta )(1-\theta )& 0& 0& -a_4& 0& 0\\ 0& 0& \pi & \lambda & \psi & -\xi -\nu -\omega & 0\\ 0& 0& \sigma (1-\pi )& \gamma (1-\lambda )& \mu (1-\psi )& \xi +\nu & -\omega \end{array}\right]$(49) The three eigenvalues are negative. i.e. $y_1=y_2=-\omega ,y_3=-\xi -\nu -\omega$ and the following characteristic equation can be used to find the remaining eigenvalues. $y^4+c_1{y}^3+c_2{y}^2+c_{3}y+c_4=0$ where $\begin{array}{rl}{c}_1& =a_1+a_2+a_3+a_4\\ c_2& =a_2{a}_3+a_2{a}_4+a_3{a}_4+a_1(a_2+a_3+a_4)(1-{\mathcal{R}}_0)+(a_2+a_4){\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_3}}\\ & +(a_2+a_3){\displaystyle \frac{\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_4}}+(a_3+a_4){\displaystyle \frac{\mathrm{\aleph }\theta }{a_2}}\\ c_3& =a_2{a}_3{a}_4+a_1(a_3{a}_4+a_2{a}_3+a_2{a}_4)(1-{\mathcal{R}}_0)+{\displaystyle \frac{a_3{a}_4\mathrm{\aleph }\theta }{a_2}}+{\displaystyle \frac{a_2{a}_3\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_4}}\\ & +{\displaystyle \frac{a_2{a}_4\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_3}}\\ c_4& =a_1{a}_2{a}_3{a}_4(1-{\mathcal{R}}_0)\end{array}$ In the above expressions, the coefficients $c_2$, $c_3$ and $c_4$ are positive when ${\mathcal{R}}_0<1$, and the coefficient $c_1$ is positive. Further, the Routh-Hurwitz criteria for fourth-order polynomials are $c_i>0,i=1,2,3,4$, $c_1{c}_2{c}_3>c_3{}^2+c_4{c}_1{}^2$ can be easily satisfied by using the coefficients listed above. So, the model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) at ${\mathrm{\Psi }}_0$ is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1.$

We equate system (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) to zero and solve simultaneously to identify an infectious equilibrium point. Thus, the endemic equilibrium is $\begin{array}{rl}{\mathrm{\Psi }}^{\ast }& =(S^{\ast },E^{\ast },I_1^{\ast },I_2^{\ast },I_3^{\ast },H^{\ast },R^{\ast })\\ S^{\ast }& ={\displaystyle \frac{\mathrm{\Lambda }}{\omega +\vartheta }},I_1{}^{\ast }={\displaystyle \frac{\theta }{a_2}}{E}^{\ast },I_2{}^{\ast }={\displaystyle \frac{\delta (1-\theta )}{a_3}}{E}^{\ast },I_3{}^{\ast }={\displaystyle \frac{\tau (1-\delta )(1-\theta )}{a_4}}{E}^{\ast }\\ H^{\ast }& ={\displaystyle \frac{{\displaystyle \frac{\pi \theta }{a_2}}+{\displaystyle \frac{\lambda \delta (1-\theta )}{a_3}}+{\displaystyle \frac{\psi \tau (1-\delta )(1-\theta )}{a_4}}}{\xi +\nu +\omega }}{E}^{\ast }\\ R^{\ast }& ={\displaystyle \frac{\sigma (1-\pi )I_1{}^{\ast }+\gamma (1-\lambda )I_2{}^{\ast }+\mu (1-\psi )I_3{}^{\ast }+(\xi +\nu )H^{\ast }}{\omega }}\end{array}$ and $E^{\ast }={\displaystyle \frac{\vartheta S^{\ast }}{a_1}}$ which satisfy the quadratic equation $({\displaystyle \frac{\mathrm{\aleph }\theta }{a_2}}+{\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_3}}+{\displaystyle \frac{\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_4}})(E^{\ast }-{\displaystyle \frac{a_1}{\mathrm{\Lambda }}}{E}^{\ast 2})-{\displaystyle \frac{a_1^2{E}^{\ast 2}\omega {\mathcal{R}}_0}{\mathrm{\Lambda }\vartheta }}=0$ Only for ${\mathcal{R}}_0>1$ does a positive endemic equilibrium point exist, whereas for ${\mathcal{R}}_0<1$, no endemic equilibrium exists.

Theorem 2.6

If ${\mathcal{R}}_0\le 1$, then the disease-free equilibrium point ${\mathrm{\Psi }}_0$ in Equation (46(46) ${\mathrm{\Psi }}_0=(S^0,E^0,I_1{}^0,I_2{}^0,I_3{}^0,H^0,R^0)=({\displaystyle \frac{\mathrm{\Lambda }}{\omega }},0,0,0,0,0,0).$(46) ) is globally asymptotically stable on a positively invariant region Θ.

Proof.

Consider the Lyapunov function: (50) $k(t)=bE(t)+c{I}_1(t)+\mathrm{d}{I}_2(t)+e{I}_3(t)$(50) Differentiate the Lyapunov function $k(t)$ at a time t in Caputo fractional derivative, we obtain (51) $D^{\alpha }k(t)=b{D}^{\alpha }E(t)+c{D}^{\alpha }{I}_1(t)+\mathrm{d}{D}^{\alpha }{I}_2(t)+e{D}^{\alpha }{I}_3(t)$(51) Substituting appropriate value from the model Equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) $\begin{array}{rl}{D}^{\alpha }k(t)& =b{\displaystyle \frac{\mathrm{\aleph }(I_1+\epsilon I_2+\varpi I_3)}{N}}S-b{a}_{1}E+c\theta E-c{a}_2{I}_1+\mathrm{d}\delta (1-\theta )E-d{a}_3{I}_2\\ & +e\tau (1-\delta )(1-\theta )E-e{a}_4{I}_3\end{array}$ As $S\le S_0$ and $S_0\approx N_0$, $\begin{array}{rl}& \le b\mathrm{\aleph }{I}_1+b\epsilon \mathrm{\aleph }{I}_2+b\varpi \mathrm{\aleph }{I}_3-b{a}_{1}E+c\theta E-c{a}_2{I}_b+\mathrm{d}\delta (1-\theta )E-d{a}_3{I}_2\\ & +e\tau (1-\delta )(1-\theta )E-e{a}_4{I}_3\end{array}$ Choose, $c={\displaystyle \frac{b\mathrm{\aleph }}{a_2}},\mathrm{d}={\displaystyle \frac{b\epsilon \mathrm{\aleph }}{a_3}},e={\displaystyle \frac{b\varpi \mathrm{\aleph }}{a_4}}$ $\begin{array}{rl}& =-b{a}_{1}E+({\displaystyle \frac{b\mathrm{\aleph }\theta }{a_2}}+{\displaystyle \frac{b\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_3}}+{\displaystyle \frac{a_b\varpi \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_4}})E\\ & =({\displaystyle \frac{\mathrm{\aleph }\theta }{a_1{a}_2}}+{\displaystyle \frac{\epsilon \mathrm{\aleph }\delta (1-\theta )}{a_1{a}_3}}+{\displaystyle \frac{\sigma \mathrm{\aleph }\tau (1-\delta )(1-\theta )}{a_1{a}_4}}-1)b{a}_{1}E\\ & =({\mathcal{R}}_0-1)b{a}_{1}E\end{array}$ There are no negative model parameters; it follows that $D^{\alpha }k(t)\le 0$ for ${\mathcal{R}}_0\le 1$ and $D^{\alpha }k(t)=0$ if and only if, E = 0. As a result, if ${\mathcal{R}}_0\le 1$, ${\mathrm{\Psi }}_0$ is globally asymptotically stable in a positively invariant region Θ, according to LaSalle's invariance principle.

2.3. The Chebyshev spectral collocation method for the solutions of SEI${}_1$I${}_2$I${}_3$HR model

Consider the fractional SEI${}_1$I${}_2$I${}_3$HR model of COVID-19 of the type given in Equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ). To apply the shifted Chebyshev polynomials of the fourth type collocation method, we first approximate $S(t)$, $E(t)$, $I_1(t),I_2(t),I_3(t),H(t),$ and $R(t)$ in terms of these polynomials with m = 3 and $0<\alpha \le 1$ as: (52) $\{\begin{array}{l}{\displaystyle S(t)=\sum _{i=0}^3{a}_i{W}_i^{\ast }(t),E(t)=\sum _{i=0}^3{b}_i{W}_i^{\ast }(t),I_1(t)=\sum _{i=0}^3{c}_i{W}_i^{\ast }(t),}\\ {\displaystyle I_2(t)=\sum _{i=0}^3{d}_i{W}_i^{\ast }(t),I_3(t)=\sum _{i=0}^3{e}_i{W}_i^{\ast }(t),H(t)=\sum _{i=0}^3{f}_i{W}_i^{\ast }(t),}\\ {\displaystyle R(t)=\sum _{i=0}^3{g}_i{W}_i^{\ast }(t),}\end{array}$(52) Now, using the concept of Lemma 1.1 and Equation (52(52) $\{\begin{array}{l}{\displaystyle S(t)=\sum _{i=0}^3{a}_i{W}_i^{\ast }(t),E(t)=\sum _{i=0}^3{b}_i{W}_i^{\ast }(t),I_1(t)=\sum _{i=0}^3{c}_i{W}_i^{\ast }(t),}\\ {\displaystyle I_2(t)=\sum _{i=0}^3{d}_i{W}_i^{\ast }(t),I_3(t)=\sum _{i=0}^3{e}_i{W}_i^{\ast }(t),H(t)=\sum _{i=0}^3{f}_i{W}_i^{\ast }(t),}\\ {\displaystyle R(t)=\sum _{i=0}^3{g}_i{W}_i^{\ast }(t),}\end{array}$(52) ) on the model Equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ), we obtaine: $\begin{array}{rl}& \sum _{i=1}^3\sum _{k=1}^i{a}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\mathrm{\Lambda }-\sum _{i=0}^3(\frac{\mathrm{\aleph }\sum _{i=0}^3(c_i+\epsilon d_i+\varpi e_i)W_i^{\ast }(t)}{N}+\omega )a_i{W}_i^{\ast }(t),\\ & \sum _{i=1}^3\sum _{k=1}^i{b}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\left({\displaystyle \frac{\mathrm{\aleph }\sum _{i=0}^3(c_i+\epsilon d_i+\varpi e_i)W_i^{\ast }(t)}{N}}\right)\\ & a_i-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )b_i)W_i^{\ast }(t)\\ & \sum _{i=1}^3\sum _{k=1}^i{c}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\theta b_i-(\pi +\sigma (1-\pi )+\omega )c_i)W_i^{\ast }(t),\\ & \sum _{i=1}^3\sum _{k=1}^i{d}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\delta (1-\theta )b_i-(\lambda +\gamma (1-\lambda )+\omega )d_i)W_i^{\ast }(t)\\ & \sum _{i=1}^3\sum _{k=1}^i{e}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\tau (1-\delta )(1-\theta )b_i-(\psi +\mu (1-\psi )+\omega )e_i)W_i^{\ast }(t),\\ & \sum _{i=1}^3\sum _{k=1}^i{f}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\pi c_i+\lambda d_i+\psi e_i-(\xi +\nu +\omega )f_i)\\ & \sum _{i=1}^3\sum _{k=1}^i{g}_i{\gamma }_{i,k}^{(\alpha )}{t}^{i-k-\alpha }=\sum _{i=0}^3(\sigma (1-\pi )c_i+\gamma (1-\lambda )d_i+\mu (1-\psi )e_i\\ & +(\xi +\nu )f_i-\omega g_i)W_i^{\ast }(t),\end{array}$ We use roots of shifted Chebyshev polynomial $W_3^{\ast }(t)$ for suitable collocation points. Also, by substituting Equation (52(52) $\{\begin{array}{l}{\displaystyle S(t)=\sum _{i=0}^3{a}_i{W}_i^{\ast }(t),E(t)=\sum _{i=0}^3{b}_i{W}_i^{\ast }(t),I_1(t)=\sum _{i=0}^3{c}_i{W}_i^{\ast }(t),}\\ {\displaystyle I_2(t)=\sum _{i=0}^3{d}_i{W}_i^{\ast }(t),I_3(t)=\sum _{i=0}^3{e}_i{W}_i^{\ast }(t),H(t)=\sum _{i=0}^3{f}_i{W}_i^{\ast }(t),}\\ {\displaystyle R(t)=\sum _{i=0}^3{g}_i{W}_i^{\ast }(t),}\end{array}$(52) ) in the positive initial conditions (19(19) $S(0),E(0),I_1(0),I_2(0),I_3(0),H(0),R(0).$(19) ), we can obtain seven equations (53) $\{\begin{array}{l}{\displaystyle \sum _{i=0}^3(-1{)}^i{a}_i=S\left(0\right),\sum _{i=0}^3(-1{)}^i{b}_i=E\left(0\right),\sum _{i=0}^3(-1{)}^i{c}_i=I_1\left(0\right),\sum _{i=0}^3(-1{)}^i{d}_i=I_2\left(0\right),}\\ {\displaystyle \sum _{i=0}^3(-1{)}^i{e}_i=I_3\left(0\right),\sum _{i=0}^3(-1{)}^i{f}_i=H\left(0\right),\sum _{i=0}^3(-1{)}^i{g}_i=R\left(0\right),}\end{array}$(53) Then, we have 28 equations that can be solved using inexact Newton's method, for the unknowns $a_i,b_i,c_i,d_i,e_i,f_i,$ and $g_i,$ for $i=0,1,2,3$.

3. Result and discussion

3.1. Numerical simulation

Numerical solutions for the model SEI${}_1$I${}_2$I${}_3$HR is made based on the real data of COVID-19 confirmed cases of Ethiopia for 101 days from 29 February 2021 to 7 June 2021 [11]. Ethiopia's total population is approximately $N=1.17\times {10}^8$, with a life expectancy of 67.8 years in 2021. As a result, the natural death rate is calculated as $\omega =1/67.8\mathrm{years}=0.0000404\mathrm{per}\mathrm{day}$. Further, from 5724 tests performed on 29 February 2021, in Ethiopia 935 new confirmed COVID-19 cases were reported. Of these, 33 were infected cases in age 0-14 years (3.12 % of the newly confirmed cases), 703 were infected cases in age 15–54 years (71.9% of the newly confirmed cases), and the remaining 199 were infected cases in age greater than 54 years. On this day, there were 954 newly recovered COVID-19 cases and 20,144 active cases (cases on treatments). The initial population is assumed $N(0)=117,027,757$. The parameter Λ is calculated from the relation $\mathrm{\Lambda }=\upsilon N=4728$ per day.

A numerical simulation will be performed based on the reported cases in Ethiopia, with the following initial conditions for the system (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ): $\begin{array}{rl}& S(0)=1.17\times {10}^8,E(0)=5724,I_1(0)=33,I_2(0)=703,\\ & I_3(0)=199,H(0)=20,144,R(0)=954\end{array}$ Sensitivity analysis of ${\mathcal{R}}_0$: Sensitivity analysis is important for identifying parameters that can be targeted in designing control strategies. The index measures the relative change in ${\mathcal{R}}_0$ with respect to the relative change in the parameters [42, 43]. Based on the epidemiological parameters in Table 1, we performed the sensitivity of the basic reproduction number ${\mathcal{R}}_0$. Changes in ${\mathcal{R}}_0$ are associated with changes in different parameters of the model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) at their given values in this analysis.

The sensitivity of ${\mathcal{R}}_0$ with respect to a model parameter r is given by (54) $S_{{\mathcal{R}}_0}^r={\displaystyle \frac{r}{{\mathcal{R}}_0}}{\displaystyle \frac{\mathrm{\partial }{\mathcal{R}}_0}{\mathrm{\partial }r}}$(54)

Table 1. Best fitted, assumed and calculated parameters used in model (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ).

Parameter	Value (${\mathrm{day}}^{-1}$)	Source	Parameter	Value (${\mathrm{day}}^{-1}$)	Source
Λ	4728	Calculated	π	0.1797	Fitted
ℵ	0.8896	Fitted	σ	0.1511	Fitted
ε	0.2701	Assumed	λ	0.1080	Fitted
ϖ	0.6288	Fitted	γ	0.0388	Fitted
ω	0.0000404	Calculated	ψ	0.7635	Fitted
θ	0.0055	Fitted	µ	0.0432	Fitted
δ	0.0258	Fitted	ξ	0.0359	Fitted
τ	0.0279	Fitted	ν	0.00016	Calculated

From Table 2, the most sensitive parameters are the transmission rate (ℵ), the contact rate from the infected people in age 15–54 years to the susceptible people (ε), the rate of hospitalization for the infected cases in age 15–54 years (λ), the contact rate from the infected people in age greater than 54 years to the susceptible people (ϖ), and the rate of hospitalization for the infected cases in age greater than 54 years (ψ). These parameters have a significant effect on the value of the basic reproduction number ${\mathcal{R}}_0$. Decreasing the rate of transmission ℵ gives a reduction in the value of the basic reproduction number ${\mathcal{R}}_0$. It would be very effective in reducing the basic reproduction number if the virus's transmission in the population could be controlled. Similarly, decreasing the parameters ε, ϖ, δ and θ which are the contact rate from infected cases age 15–54 years to the susceptible population, the contact rate from the infected cases age above 54 years to the susceptible population, the rate of progression from exposed to infected group age 15–54 years, the rate of progression from exposed to the infected group age less than 14 years, respectively, lead to the decrease in the value of the basic reproduction number ${\mathcal{R}}_0$. Also, increasing the values of the parameters λ, ψ, and π which are the rate of hospitalization for infected cases age 15–54 years, above 54 years, and less than 14 years, respectively, lead to the decreasing on the value of the basic reproduction number ${\mathcal{R}}_0$. The best strategies for controlling the pandemic are to reduce the rate of transmission in the population and to improve the treatment of patients in treatment centres. When all other parameters are kept constant, the value of each parameter that gives a stable reproduction number (${\mathcal{R}}_0\le 1$) is as follows: $\mathrm{\aleph }\le 0.6568,\epsilon \le 0.14152,\varpi \le 0.00012,\lambda \ge 0.2050$ Other parameters change within their suitable range, making all their own effects, even the value of the reproduction number greater than or less than one.

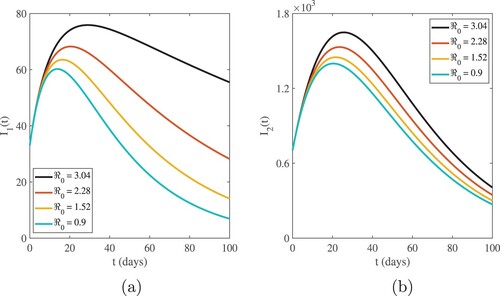
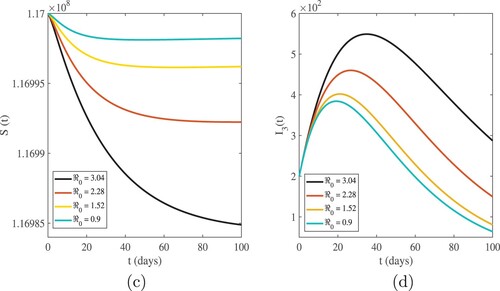
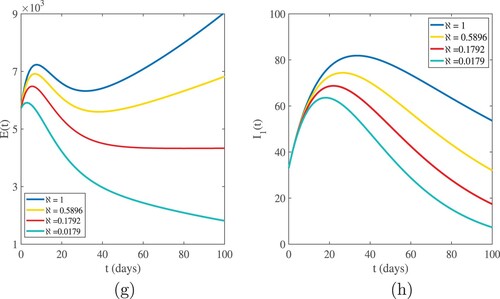
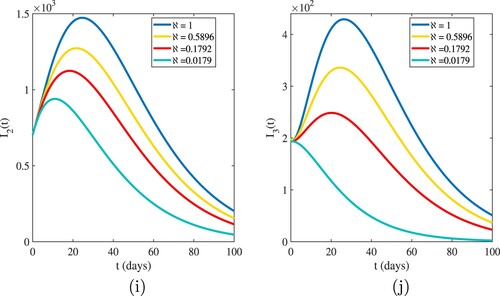
The graphical interpretations of Figures 4 and 5 show the behaviour of our numerical results for susceptible and infected population based on different values of ${\mathcal{R}}_0$.

Figure 4. Numerical results of I${}_1(t)$ and I${}_2(t)$ for different values of ${\mathcal{R}}_0$.

Figure 5. For various values of ${\mathcal{R}}_0$, numerical results of $S(t)$ and I${}_3(t)$.

Table 2. Sensitivity of the basic reproduction number ${\mathcal{R}}_0$ with respect to epidemiological parameters in Table 1.

Parameter	Sensitivity index	Parameter	Sensitivity index
ℵ	1.000	π	−0.1033
ε	0.5470	σ	−0.0839
ϖ	0.2474	λ	−0.3980
θ	0.1111	γ	−0.1327
δ	0.1125	ψ	−0.2336
τ	−0.2165	µ	−0.0330

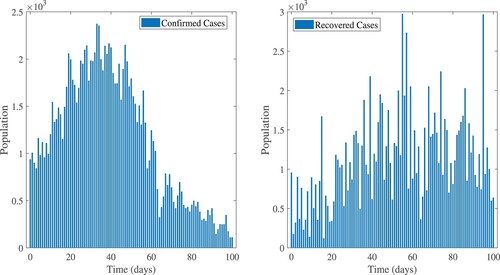
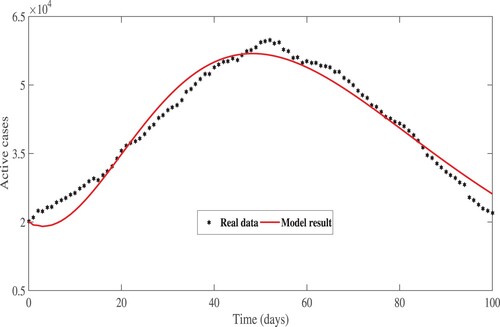
In Figures 6 and 7, we compared the SEI${}_1$I${}_2$I${}_3$HR model results to the EPHI data of daily reported cases in all age groups and daily active cases for the 2019 Coronavirus disease in Ethiopia. The simulated results are very close to actual data on infected and active cases obtained from the Ethiopia Ministry of Health and the Ethiopia Public Health Institute daily report for a 101-day period starting 29 February 2021.

Figure 6. In Ethiopia, real data and model results for daily infected cases between 29 February 2021 and 7 June 2021.

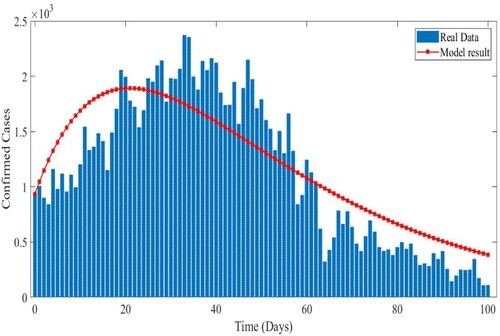
Figure 7. Real data and model result for daily active cases between 29 February 2021 and 7 June 2021.

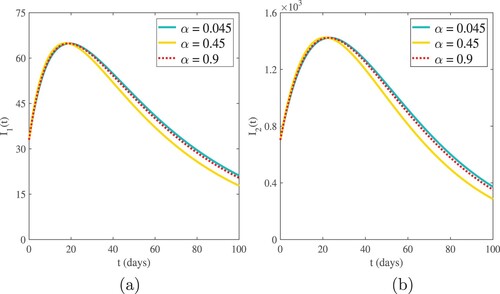
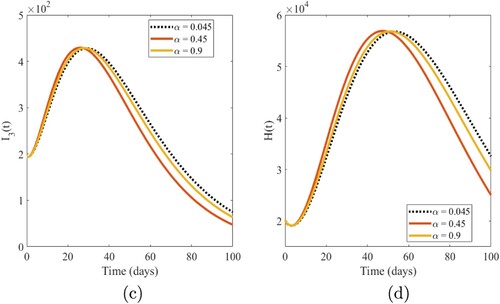
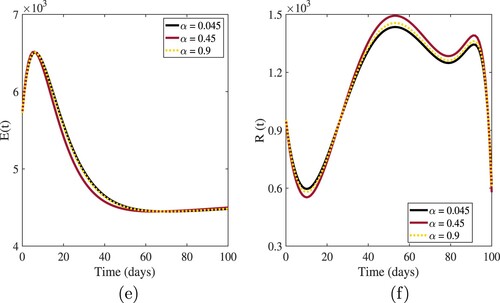
The influence of fractional-order α on numerical solutions of the model compartments is shown in the graphical interpretations of Figures 8–10.

Figure 8. Approximate solutions of I${}_1(t)$ and I${}_2(t)$ for different α.

Figure 9. Approximate solutions of I${}_3(t)$ and $H(t)$ for different α.

Figure 10. Approximate solutions of $E(t)$ and $R(t)$ for different α.

3.2. Discussion

The reported data for confirmed, recovered, tests performed, and death cases in Ethiopia are shown in Figures 2 and 3. In Equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ), Table 1 provides the fitted, computed, and assumed parameters of a model. The fitted parameters were generated using least square curve fitting in MATLAB R2020a and real data was made available in Ref. [11]. Table 2 also discusses the sensitivity of the basic reproduction number ${\mathcal{R}}_0$, and it is concluded that the transmission rate ℵ is the most sensitive parameter. This parameter influences ${\mathcal{R}}_0$ in a positive way. That is, decreasing transmission rate values results in decreasing ${\mathcal{R}}_0$ values. Keeping the other values in Table 1 unchanged and reducing the transmission rate from 0.8896 to 0.1896, ${\mathcal{R}}_0$ reduces from 1.3545 to 0.2887. In addition, hospitalization rates for each age group of infected individuals have a negative impact on ${\mathcal{R}}_0$. In other words, increasing the values of these parameters lowers the quantity of ${\mathcal{R}}_0$. Figures 4 and 5 show that the highest value of the basic reproduction number ${\mathcal{R}}_0$ shows the highest number of cases in all age categories, and as the number of infected cases increases, the susceptible population decreases. For ${\mathcal{R}}_0=3.04>1$, we have evidence that in this simulation, most of the susceptible individuals are rapidly decreasing and the infected cases are increasing. This indicates that one infected person will cause more than three new infections, and virus transmission will become uncontrollable. When the basic reproduction number ${\mathcal{R}}_0=0.9<1$ is used, the curves reveal that susceptible people increase and converge to the population's initial number, while infected individuals tend to be few. This indicates that the number of newly infected individuals is decreasing, that society is safe from the virus, and that the infection will eventually die out in the country. The comparison of real data and model findings for daily confirmed cases and active cases in Ethiopia is shown in Figures 6 and 7. The reader may see from these illustrations that mathematical models have a lot of strength when it comes to expressing real-world problems. Figures 11 and 12 illustrate how lowering the transmission rate of the coronavirus due to infected cases in all age groups can help to slow the disease's progress. The basic reproduction number ${\mathcal{R}}_0$ will be reduced from 1.3545 to 0.9991 by decreasing the transmission rate from 0.8896 to 0.6562 per day. 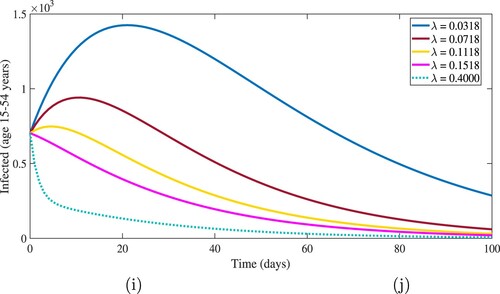As a result, when $\mathrm{\aleph }\le 0.6562$, a stable disease-free equilibrium is obtained. Figure 13 shows how increasing the rate of hospitalization for infected cases (age 15–54 years) reduces the number of infected cases by a significant amount. When $\lambda =0.0318,0.0718,0.1118$, $0.1518$ and $0.4000$, the corresponding basic reproduction number ${\mathcal{R}}_0=2.1363,1.5940$, $1.3366,1.3058,$ and 0.8404, respectively. For the real data of COVID-19 cases in Ethiopia, the parameters in Table 1 produced a value of the basic reproduction number ${\mathcal{R}}_0=1.3545$, which exceeds unity. This number indicates that the disease-free equilibrium point for model Equation (18(18) $\begin{array}{l}{D}^{\alpha }S(t)=\mathrm{\Lambda }-(\vartheta +\omega )S,\\ D^{\alpha }E(t)=\vartheta S-(\theta +\delta (1-\theta )+\tau (1-\delta )(1-\theta )+\omega )E,\\ D^{\alpha }{I}_1(t)=\theta E-(\pi +\sigma (1-\pi )+\omega )I_1,\\ D^{\alpha }{I}_2(t)=\delta (1-\theta )E-(\lambda +\gamma (1-\lambda )+\omega )I_2,\\ D^{\alpha }{I}_3(t)=\tau (1-\delta )(1-\theta )E-(\psi +\mu (1-\psi )+\omega )I_3,\\ D^{\alpha }H(t)=\pi I_1+\lambda I_2+\psi I_3-(\xi +\nu +\omega )H,\\ D^{\alpha }R(t)=\sigma (1-\pi )I_1+\gamma (1-\lambda )I_2+\mu (1-\psi )I_3+(\xi +\nu )H-\omega R,\end{array}\}$(18) ) is locally asymptotically unstable, whereas the infectious equilibrium point is stable, implying that the coronavirus will persist in the population, as evidenced by the infectious population remaining positive in this numerical simulation. The transmission from infected cases aged below 14 years is ${\mathcal{R}}_{0I_1}=0.2767$, which contributes 20.43% of the basic reproduction number, the transmission from infected cases age 15-54 years, ${\mathcal{R}}_{0I_2}=0.7422$ contributes the largest value 54.79% of the basic reproduction number and the transmission from infected cases aged greater than 54 years ${\mathcal{R}}_{0I_3}=0.3356$, which contributes 24.78%. To control the spread of this virus in Ethiopia, managing transmission from infected cases in the age group of 15–54 years is pivotal and the Ethiopian government and all the responsible bodies should focus on transmission due to infected cases in the age group of 15–54 years.

Figure 11. Decreasing the transmission rate on the approximate solutions of E(t) and I${}_1(t)$ at $\alpha =0.45$.

Figure 12. Decreasing the transmission rate on the approximate solutions of I${}_2(t)$ and I${}_3(t)$ at $\alpha =0.45$.

Figure 13. Increasing the hospitalization rate on the approximate solution of I${}_2(t)$ at $\alpha =0.45$.

4. Conclusion

In this paper, we have investigated the spread of COVID-19 disease using SEI${}_1$I${}_2$I${}_3$HR model and in the Caputo sense the model is presented as a system of fractional-order differential equations, with the numerical solutions achieved using the Chebyshev polynomials of the fourth kind. The proposed model is converted to a nonlinear system of algebraic equations that are solved using Newton's iteration method using the properties of this polynomial. The findings of the proposed model are found to be very close to the real data. The identification of key parameters that have a huge effect on basic reproduction number is important for creating the most effective and efficient disease prevention methods. The value of the basic reproductive number ${\mathcal{R}}_0>1$ shows that one COVID-19 tested positive person is the cause of more than one new infected individual. Therefore, the coronavirus spread is going on. As a result, we recommended everybody who is responsible for fully participating in reducing the value of the basic reproductive number to less than unity. The transmission rate plays a significant role in reducing the basic reproduction number, according to the simulated results in this work. For disease control, reducing virus transmission in the population is critical. Throughout the pandemic, the Ethiopian government must take the necessary steps to control strategy toward reducing ${\mathcal{R}}_0$ through sensitive parameters.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Data from COVID-19 cases in Ethiopia from 29 February 2021 to 7 June 2021 were utilized to support this investigation.