Ab initio identified design principles of solid-solution strengthening in Al

Abstract

Solid-solution strengthening in six Al–X binary systems is investigated using first-principle methods. The volumetric mismatch parameter and the solubility enthalpy per solute were calculated. We derive three rules for designing solid-solution strengthened alloys: (i) the solubility enthalpy per solute is related to the volumetric mismatch by a power law; (ii) for each annealing temperature, there exists an optimal solute–volume mismatch to achieve maximum strength; and (iii) the strengthening potential of high volumetric mismatch solutes is severely limited by their low solubility. Our results thus show that the thermodynamic properties of the system (here Al–X alloys) set clear upper bounds to the achievable strengthening effects owing to the reduced solubility with increasing volume mismatch.

• 10.07
• 30.05
• 30.06

• ab initio
• DFT
• Al alloys
• solid-solution strengthening
• solubility
• alloy design

1. Introduction

The rapid, physics-based development of materials with tailored properties that match the demands of modern manufacturing and design is probably the most important challenge in modern materials science. The fine-tuning of properties during the materials design process is essentially a multi-criteria optimization, in which secondary aspects, such as the availability of components, are often also of decisive importance (see e.g. [1]). To accelerate this optimization, a theory-guided materials design concept has recently been proposed in which the most promising candidates are pre-selected employing theoretical tools (see e.g. [2]) before experimentally casting and testing materials.

In this paper, we aim to identify and analyze fundamental limitations related to one of the most important strengthening mechanisms, namely solid-solution strengthening (see e.g. [3, 4]). It is a typical multi-criteria concept that is controlled not only by the solute strengthening capability [5–7], but also by thermodynamic properties of the solute–solvent system, such as the solubility. Therefore, a universal solid-solution design function that combines the strengthening capability with the solubility is of considerable interest for the physics-based design of advanced metallic alloys. To identify these relations, we exploit the facts that the volumetric mismatch is by far the dominant contribution to the strengthening effect [7] and that T = 0 K ab initio calculated lattice parameters (of static lattices without considering thermal vibrations) reproduce experimental data typically within −5% to 3% at T = 0 K [8, 9] (for calculations also considering harmonic and quasi-harmonic approximations to thermal vibrations, see e.g. [10–13]).

The design rules we derive not only provide a guideline for a more efficient alloy design but also theoretically explain the experimentally observed inverse relationship between the solubility of a solute and its strengthening capability (see Ni, Cu and Au binaries [14] or α-Fe binaries [15]). As a higher strength is often accompanied by a lower ductility, identifying the limitations of solid-solution strengthening can also help in revealing the limitations of ductility. Besides, modeling the solid-solution strengthening effect is an essential step in multiscale modeling schemes aimed at designing Al alloys with high formability [16].

2. Methods and computational details

The relation between the strengthening effect and the solubility, as well as the resulting alloy-design limits, is investigated in aluminum, which is a prototypical soft material with numerous structural applications. Employing density functional theory (DFT) calculations [17, 18], six Al binary systems (Al–X, X = Ca, Sr, Ir, Cu, Li and Zn) have been studied. It was recently shown by Leyson et al [6, 19] that the volumetric mismatch can be correlated with the strengthening capability in Al solid solutions via the volumetric mismatch parameter (|δ_b|). We extend this analysis to express the equilibrium solute concentration in terms of δ_b. The impurity concentration in thermodynamic equilibrium is determined by the solubility enthalpy per solute (). Following [20], this quantity is expressed as 1 where 2 3 is the formation enthalpy per solute of the solid solution; is the formation enthalpy per solute of the nearest intermetallic compound located in the Al–X phase diagrams next to the Al–X solid solutions, i.e. above the solubility limit. To calculate , the energies of the intermetallic phases in the vicinity of the Al–X solid solution on the Al–X phase diagrams have been determined (see details below).

Our DFT calculations were performed employing 32- and 108-atom fcc-based 2 × 2 × 2 and 3 × 3 × 3 supercells with the compositions of Al₁₀₇X₁, Al₁₀₅X₃, Al₃₁X₁, Al₁₀₄X₄ and Al₃₀X₂. For these low solute concentrations the calculated compositional trends in the formation enthalpy and lattice parameters of the solid solutions may be linearized, i.e. they depend linearly on the concentration. A full geometry optimization was performed in all cases. We used the generalized gradient approximation of Perdew et al [21] for the exchange-correlation functional and the projector augmented wave method [22], as implemented in the VASP code [23, 24]. The electronic wave functions were expanded in terms of a plane-wave basis set with an energy cut-off of 420 eV, and the reciprocal-space Brillouin zone was sampled using a 24 × 24 × 24 Monkhorst–Pack [25] k-point mesh/conventional fcc unit cell, namely 12 × 12 × 12 for 32-atom supercells and 8 × 8 × 8 for 108-atom supercells. The Methfessel–Paxton smearing method of first order was used to smear the Fermi surface with the smearing parameter σ = 0.4 eV [26]. The energy–volume curves were analyzed using the Birch–Murnaghan equation of state [27, 28]. After the equilibrium lattice parameters are obtained, the volumetric mismatch parameter, δ_b, can be calculated as 4 This parameter, proposed by Cottrell [29], is based solely on the geometrical arguments. There is another parameter which characterizes the volumetric mismatch. It was proposed by Eshelby [30] and is usually referred to as ‘the strength of the point defect’. This parameter essentially characterizes the stress/strain response of a crystal containing a single point defect to external strain/stress fields. Since most of the interaction energy between the dislocation and the solute comes from the excess volume introduced by the solute against the pressure field produced by the dislocations, ‘the strength of the point defect’ is more pertinent in the context of the solid-solution strengthening. On the other hand, by using atomistic simulation, it has been shown that in fcc substitutional solid solutions, the volume mismatch parameter proposed by Cottrell can be used to accurately predict the interaction energy between the dislocation and solute [31], mostly because the dilatation center caused by a substitutional atom in fcc lattice is spherical [32].

To calculate the ground state total energy of the ordered compounds, we used the same cut-off energy and exchange-correlation functional. Different k-point meshes were chosen according to the symmetry of the corresponding lattice structures: (i) a 16 × 16 × 12 k-point mesh for Al₄Ca and Al₄Sr (five-atom cell with the I4/mmm space group, D1₃ structure of Al₄Ba), (ii) a 16 × 16 × 16 mesh for Al₂Cu (six-atom cell I4/mcm, C16 structure, Al₂Cu prototype) and (iii) a 16 × 16 × 24 mesh in the case of AlLi (four-atom , B32 structure of NaTl) and AlIr (two-atom , D8_d, Co₂Al₉ prototype). In the Al–Zn binary system, there are no intermetallic compounds and, therefore, the solubility enthalpy is equivalent to the enthalpy of mixing.

3. Results and discussion

Figure 1(a) shows the computed relation between the solubility enthalpy per solute and the volumetric mismatch parameter. The calculated values are summarized in table 1. The data points approximately follow a power law, namely 5 with the exponent n > 0. The fitted values of the A and n parameters are 1.92 and 0.69, respectively. The corresponding R² parameter, which allows to quantify the numerical quality of the fit, is equal to 0.9928, suggesting that the power law provides a good description of the underlying physical phenomenon. It is important to note that the value of the predicted exponent n is in excellent agreement with that proposed in the semi-empirical model of Miedema et al [33], who suggested that the enthalpy of formation of binary alloys scales with the volume Ω_B of solute atoms B in a matrix A as Ω^2/3_B.

Figure 1. (a) A log–log plot of the solubility enthalpy per solute atom () as a function of the volumetric mismatch parameter |δ_b| together with the fitting function (dashed line). In panel (b) the maximum solubility, c_m, at T = 800 K is shown as a function of (|δ_b|). Solid symbols: theory (this study); open symbols: experiments. Experimental data are included for Al–Cu [34], Al–Si [35], Al–Li [36] and Al–Zn [37]. Additionally, 1.9 at.% Ca were found at 888 K in Al–Ca [38] and 0.1 at.% Ir were found after quenching at 873 K in Al–Ir [39], but no solubility of Sr in Al has been reported so far.

Table 1. Computed values of the volumetric mismatch parameter (|δ_b|, where ) and the solubility enthalpy per solute atom ( (eV per solute)).

Al–	Ca	Sr	Ir	Cu	Si	Zn	Li
|δb|	0.364	0.540	0.183	0.106	0.0534	0.017	0.007
	1.22	2.35	1.16	0.36	0.4236	0.11	0.065

The observed functional dependence of the heat of the solution on the volumetric mismatch of the solute atom allows us to identify a few fundamental materials design limits. In particular, the strengthening potential of a specific solute will tend to be proportional to its solubility enthalpy and therefore inversely related to its solubility. This relationship reveals competition between elasto-plastic effects related to the mechanical properties, on the one hand, and the thermodynamic limits on the solubility, on the other. Specifically, according to classical solid-solution theories, the maximum strengthening effect is expected from solutes with maximum volumetric mismatch. In exactly the opposite manner, from the thermodynamic point of view, the incorporation of solutes with large volume mismatches into a lattice is energetically so costly that the solubility of these solutes will be extremely low. Therefore, the strengthening effect of such an incorporation will be very limited. It is thus the thermodynamics of the system that sets clear upper bounds on the achievable strengthening effects due to the reduced solubility with increasing volumetric mismatch.

The inverse dependence of the strengthening potential and the solubility of a solute allows substitution of an element of a high strengthening capability by an alternative element of lower strengthening potential but higher solubility. Importantly, our analysis provides guidance on the selection of such alternative solutes (via their volumetric mismatch).

In particular, employing the power law identified above, which relates the solution enthalpy per solute and the volumetric mismatch parameter |δ_b|, we can estimate the solubility limits (c_m) on the basis of |δ_b| using the Boltzmann statistics 6 The value of c_m at 800 K was calculated with equation (66 ) and compared with available experimental values shown in figure 1(b), and very good agreement was achieved. The elevated temperature of T = 800 K was chosen because (i) it is common practice to quench the Al solid solutions from high temperatures to room temperature in order to maintain the solid solution and (ii) the formation processes are often performed at elevated temperatures.

Based on the theoretical findings recently published by Leyson et al [6, 19], the yield strength (σ_y) of the polycrystalline solid solutions with random texture at its solubility limit c_m at temperature T can be calculated as 7 Here M_T is the Taylor factor, which is equal to approximately 3 for polycrystals with random texture; ε(ΔV ) is the strengthening capability, which depends on the excess volume (ΔV ) introduced by the solute atom; ΔE_b(ΔV ) is the energy barrier that a flexible dislocation needs to overcome when passing through an array of solute atoms. Following Leyson et al [6, 19], the strain rates and were chosen to be 10⁴ and 10⁻⁵, respectively. To evaluate equation (77 ), we again rely on the results summarized by Leyson et al [6]: 8 9 and we also consider the fact that ΔV is related to δ_b as follows. Let V and a be the atomic volume and the lattice parameter of the fcc unit cell, respectively; then 10 11 and therefore 12 where 13 a_Al is the lattice parameter of Al (4.04 Å at T = 0 K calculated by DFT in this study). We insert equations (66 ), (88 ), (99 ) and (1212 ) into equation (77 ) and also substitute the constants M_T, k_b, , and by their actual values. Then we can express σ_y (equation (77 )) solely by |δ_b| and the temperature 14 where T_a is the annealing temperature and T_t is the testing temperature. Equation (1414 ) can be applied to evaluate the yield strength when an Al solid solution is subjected to the following thermal treatment: annealed at T_a and reaches its solubility at T_a, then quenched down to T_t and tested at T_t.

Having expressed σ_y in terms of δ_b and temperature exclusively, it is possible to predict the optimum size mismatch to maximize the strengthening effect at a given temperature. It should be noted that two temperatures have to be taken into account: (i) the annealing temperature, which determines the equilibrium solute concentration, and (ii) the temperature in the experimental setup, which provides the thermal activation energy for the migration of dislocations in the field of solute atoms. In our analysis, we assume that T_t = 78 K and evaluate the yield strength as a function of the annealing temperature and δ_b, as shown in figure 2. The optimum volumetric mismatch slightly increases with increasing annealing temperature and tends to be rather small, suggesting that the increased solubility outweighs the increased strengthening potential associated with a larger volumetric mismatch.

Figure 2. Dependence of the yield stress (in MPa) of polycrystalline Al solid solutions, σ_y(c_m(T),T_t = 78 K), on the annealing temperature and |δ_b|. This figure is obtained assuming the following metallurgical route: the Al solid solution with a volumetric mismatch parameter of |δ_b| is annealed at a given temperature, T_a, to reach the equilibrium solute concentration, c_m, (assuming a solute element reservoir) followed by quenching in liquid nitrogen (78 K) and tested at 78 K. The corresponding σ_y(c_m(T),T_t = 78 K) is calculated using equation (77 ). Thus, σ_y in this figure corresponds to the yield stress of polycrystalline Al solid solutions at 78 K with c_m obtained at T_a. |δ_b| of five solute elements (Li, Zn, Si, Mg and Cu) are marked by lines. Since quantum-mechanical calculations of Mg were not performed in this study, Mg results derived from the literature are marked by a dashed line.

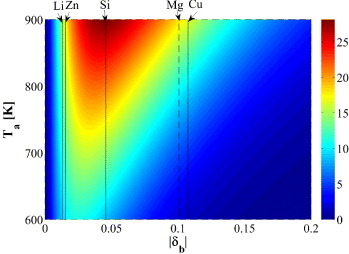
The theoretical prediction in this study may be indirectly validated by the experiments reported in [40]. In that study, the solid-solution strengthening effect was investigated at room temperature in five Al binary systems, and the solute elements included Mn, Cu, Mg, Si and Zn (in descending order of their |δ_b|). It was observed that although the strengthening capabilities of Mn and Cu in Al are higher than Mg, Mg has the advantage of being more soluble in Al; therefore, a higher solid-solution strengthening effect can be achieved in Al–Mg. Zn has a higher solubility in Al than Mg, but its strengthening effect is limited. Our results for Si indicate that this element provides maximum strengthening effects. This finding is in accord with the fact that commercially used 5XXX and 6XXX Al-alloys contain significant amounts of Si (next to Mg and Cu, which are also quite close to the maximum).

Figure 2 shows an extrapolation of the predicted σ_y for solutes for which experimental data exist in the literature (such as Mn [6]). It indicates that our theoretical prediction underestimates σ_y by a factor of 6 or more (depending on the solute type). This quantitative disagreement with experimental critical shear stresses in Al is tentatively attributed to our disregarding entropic contributions when calculating the solution enthalpy.

Some entropy contributions (such as vibrational) would be part of the free energies of nearly all the systems involved, i.e. Al-based solid solutions, ground-state phases of pure elements, as well as ordered intermetallics. Others would only affect calculations of some of the computed systems, such as the configurational entropy term in the case of solid solutions. In particular, vibrational contributions to the free energy have been shown to significantly affect the solubility of solutes in Al. When the vibrational entropy is included, the calculated solubility grows in Al–Sc and Al–Si solid solutions [41]. These contributions can be taken into account following the approaches discussed in [10–13]. However, while the predicted critical shear stress may not be quantitatively correct, the fundamental conclusions, for example, that the optimal value tends to be small, are not affected by this additional consideration.

4. Conclusions

We have theoretically studied the relations between the solid-solution strengthening effect and the solubility in six Al binary alloys using DFT. Based on the materials parameters calculated within this supercell approach, we have quantitatively analyzed the solubility enthalpy per solute and the volumetric mismatch parameter |δ_b|. We find that these are related by a power law whose exponent matches the scaling proposed by Miedema et al in their semi-empirical model. Based on this relation, we link the thermodynamic characteristics of the studied systems with their macro-scale critical shear stress.

Using this insight we show that, at a given annealing temperature, there exists an optimal volumetric mismatch |δ_b| (or equivalently an ideal solute element, if available in nature) to achieve the maximum strengthening effect, which is controlled by the solubility limit (c_m). The optimum mismatch is generally relatively small, in accordance with the classical Hume–Rothery rules, and increases with increasing temperature. Lastly, the strengthening capabilities of the elements with high volumetric mismatch parameters are severely limited by their low solubility. Our analysis can also be extended to alloys containing more than one type of solute atom. Regarding thermodynamic aspects and solubility limits, such an extension would, nevertheless, not be straightforward. As the concentration of solutes may be relatively high when reaching individual solubility limits, solute atoms are likely to interact among themselves and these interactions can lead to nonlinear effects. Further, equations (77 ) and (1414 ) are nonlinear functions of the solute concentration and the height of energy barriers, and an extension to multiple solutes is also non-trivial (see e.g. equation (32) in [6]).

We believe that these conclusions may be generalized well beyond Al solid solutions, as the fundamental physics underlying our analysis will hold in any solid-solution system. Therefore, our study may be directly applied when searching for alternative solutes for particular processing constraints, such as joinability or corrosion resistance.

Appendix

Recently, Leyson et al [42] extended their work to the Mg–Al system on the basal slip and found two dislocation configurations, namely two characteristic bow-out lengths. This finding leads to two kinds of energy barrier (ΔE_b) that a flexible dislocation needs to overcome when passing through an array of solute atoms. One controls the low-temperature/high-stress regime, and the other controls the high-temperature/low-stress regime. If the solubility enthalpies of the solute elements and their volume mismatch parameters in Mg are also correlated by power laws, the above finding does not change the present formulation (equation (77 )) for incorporating the solubility effects in Mg solid solutions, because ΔE_b depends not on concentration but rather on the extra volume introduced by the solute atoms.