Adjusting wheal size measures to correct atopy misclassification

Abstract

Purpose:

Skin prick testing (SPT) is fundamental to the practice of clinical allergy identifying relevant allergens and predicting the clinical expression of disease. Wheal sizes on SPT are used to identify atopic cases, and the cut-off value for a positive test is commonly set at 3 mm. However, the measured wheal sizes do not solely reflect the magnitude of skin reaction to allergens, but also skin reactivity (reflected in the size of histamine reaction) and other random or non-random factors. We sought to estimate wheal sizes exclusively due to skin response to allergens and propose gender-specific cutoff points of atopy.

Methods:

We developed a Bayesian method to adjust observed wheal sizes by excluding histamine and other factor effects, based on which revised cutoff points are proposed for males and females, respectively. The method is then applied to and intensively evaluated using a study population aged 18, at a location on the Isle of Wight in the United Kingdom. To evaluate the proposed approach, two sample t-tests for population means and proportion tests are applied.

Results:

Four common aeroallergens, house dust mite (HDM), grass pollen, dog dander, and alternaria are considered in the study. Based on 3 mm cutoff, males tend to be more atopic than females (P-values are between 0.00087 and 0.062). After applying the proposed methods to adjust wheal sizes, our findings suggest that misclassifications of atopy occur more often in males. Revised allergen-specific cutoff values are proposed for each gender.

Conclusion:

To reduce the gender discrepancy, we may have two potentially convenient solutions. One way is to apply allergen-specific and gender-specific cutoff values following the proposed method. Alternatively, we can revise the concentration of allergens in the SPT solutions but keep the cutoff values unchanged, which may be more convenient to clinicians.

Keywords:

• SPT
• atopy
• Bayesian method
• joint modeling
• misclassification

Introduction

Atopy is regarded as an inherited predisposition for diseases such as eczema, asthma, or rhinitis. Skin prick testing (SPT) to allergens is commonly used to identify allergic sensitization or atopy. Although some previous studies have suggested different cutoff values,^1,2 in clinical practice, a 3 millimeter (mm) cutoff wheal size on SPT is the criterion generally used to define a positive response and, therefore, sensitization. An atopic status is defined as the presence of sensitization to one or more allergens using this cutoff.

The present work is motivated by a discrepancy observed in our birth cohort between atopy and atopy-related diseases such as eczema. The cohort was established between 1989 and 1990 on the Isle of Wight (IOW) in the United Kingdom to prospectively study the natural history of allergic disorders. Skin prick testing was performed on most participants attending the research center to a standard battery of common allergens (ALK, Horsholm, Denmark), including aeroaller-gens (house dust mite, cat dander, dog dander, Alternaria, Cladosporium herbarium, grass pollen mix, and tree pollen mix) and food allergens (cows’ milk, soya, hens’ egg, peanut, and cod). In this work, we focus on individuals aged 18, which includes 405 males and 445 females. Table 1 provides sensitization prevalence for four allergens, house dust mite (HDM), grass pollen, dog dander, and Alternaria, together with percentages of eczema among sensitized cases. As shown in the table, with atopic status determined by the 3 mm cutoff, significantly more males are sensitized than females based on two-sided two-sample proportion tests (significance level is set at 0.01 after adjusting for multiple testing). However, among the atopic children, the proportion of males who developed eczema tends to be lower than (but not statistically significant based on the same type of tests) that of females, although more males are atopic. For instance, about 35% of males are sensitized to HDM, which is significantly higher than that of females (23.37%). However, among the atopic males, about 14% developed eczema, which is lower than that of females (21.15%). We also examined the other two allergic diseases, asthma and rhinitis. Comparable patterns are observed (results not shown). Although for allergen Alternaria, higher proportions of atopic males developed asthma and/or rhinitis, the differences are statistically insignificant. These observations (more atopic males but fewer with allergic diseases) conflict with the well-established positive association between atopy and atopy related diseases such as eczema and asthma.^3–5 These observed discrepancies made us wonder whether atopic status was misclassified.

Table 1 Comparison between gender of atopy prevalence and percentage of atopic cases having eczema based on 3 mm cutoff (405 males and 445 females)

Allergen	Sensitization prevalence (%)			% of atopic cases with eczema
	Males	Females	P-value	Males	Females	P-value
HDM	35.06	23.37	0.00087	14.08 (142)	21.15 (104)	0.073
Grass	26.73	21.34	0.033	13.89 (108)	18.95 (97)	0.16
Dog dander	12.35	8.99	0.056	26.00 (50)	25.00 (40)	0.46
Alternaria	9.63	6.74	0.062	17.95 (39)	20.00 (30)	0.41
All above	46.53	34.61	0.00013	12.23 (188)	20.13 (154)	0.023

Notes: The numbers of positive sensitization are included in the parentheses. Two-sided two sample proportion tests are used to test gender differences between percentages for each allergen. For tests in columns 4 and 7, respectively, multiple testing adjusted significance level is 0.0125 (0.05/5 = 0.01) using the Bonferroni method. P-values are listed to show the significance of percentage differences between gender.

To examine the existence of atopy misclassification, we first compared total immunoglobulin E (IgE) between gender in our cohort. The result shows insignificant difference between males and females (the average total IgE for males is 296.0 ng/ml vs 287.4 ng/ml for females; P-value = 0.23 from two-sided two sample t-test for population means), which agrees with findings in other studies.⁶ In addition, results from another cohort⁷ along with findings from other studies examining the agreement of atopic status determined by SPT and by specific IgEs reached the same conclusion⁸. That is, insignificant differences of atopy prevalence exist between gender based on specific IgEs but significant differences are found based on SPT. Specific IgEs and total IgE are antibody classes regarded as an important factor in the pathogenesis of allergic diseases and higher IgE measures indicate higher probabilities of allergic sensitization. This implies that we ought to expect insignificant gender difference in atopy in general populations. This conflicts with our findings on SPT testing results and consequently indicates the possible existence of misclassifications from SPT.

Since skin reactivity plays a role in the determination of wheal sizes and this reactivity, reflected in histamine wheal size, varies between gender at any given age,^1,9–11 cutoff points determined based on SPT wheal sizes without adjustment for these factors may not correctly identify allergic sensitization or determine atopic status. Thus to reduce the possibility of misclassification, two venues may be taken: adjusting the wheal sizes or proposing revised cutoff values that are gender-specific. Both directions aim to correct misclassifications, specifically non-differential misclassifications (misclassifications independent from disease or exposure status). Non-differential misclassifications can cause misleading inferences if left unchecked. In linear or logistic regressions, such errors may lead to biased estimates of coefficients.^12–14 In many situations, the misclassifications are actually caused by mismeasured continuous variables.¹⁵ This can be the situation of SPT wheal size measures in the sense that they are not exclusively a result of allergen reaction; skin reactivity also contributes to the size of a wheal.

In this article, through a Bayesian hierarchical joint modeling, we first infer wheal sizes in response exclusively to allergens, and then propose gender specific cutoff values for sensitization. The utilization of the Bayesian method was motivated by the hierarchical structure between atopy and atopy related diseases. Due to the similar discrepancy patterns observed in asthma, eczema, and rhinitis, throughout this article, we use eczema to demonstrate the method. In the Discussion section, we briefly summarize results from the other two allergic diseases. We focus on four common aeroallergens, HDM, grass pollen, dog dander, and Alternaria. These four allergens are well represented in the IOW cohort data. Other allergens are not considered due to the sparsity of positive SPT reactions or their cross-reactivity with these four allergens. We expect the work has the potential to resolve the disagreement noted above, which will consequently improve the diagnosis and management of allergic diseases.

Material and methods

We start this section by presenting the modeling of observed wheal sizes and that of the association between eczema and wheal sizes in reaction to allergen (hereafter, true wheal sizes). From the discussion above, the atopy prevalence among males is expected to agree with atopy prevalence among females in general populations, and there should not exist gender differentiated association between true wheal sizes and the risk of eczema.

Model construction

In the following, we discuss the modeling separately for observed wheal sizes, true wheal sizes, and the risk of eczema. In the next section, they are linked through a joint modeling process.

The observed wheal size

Let O_ij denote the observed wheal size of person i with gender j (j = 1 for females) in reaction to an allergen. The observed wheal size is a mixture of response to the allergen, skin reactivity and other unknown random factors. We use T_ij to denote the latent (unknown) true wheal size. The difference between the expected value of O_ij and T_ij, denoted as F_ij, is modeled as a function of histamine effects (which reflects skin reactivity) and possible interaction effects between the allergen and histamine. We formulate them as follows: $\begin{array}{l}{O}_{ij}=T_{ij}+F_{ij}+{\in }_{ij}\\ F_{ij}={\alpha }_i+{\beta }_{1ij}{H}_{ij}+{\beta }_{2ij}{T}_{ij}\times H_{ij},\end{array}$(1) where α_j denotes an overall gender effect on the observed wheal sizes and a constraint α₁ + α₂ = 0 is applied to avoid singularity, β_lij is a random slope for the contribution of histamine H_ij, and β_2ij is treated as being random as well indicating an interaction effect between allergen and histamine. The interaction is denoted as T_ij × H_ij in model (1). The random coefficients are assumed to be normally distributed with ${\beta }_{1ij}\sim N(0,{\sigma }_{{\beta }_{1j}}^2)$ and ${\beta }_{2ij}\sim N(0,{\sigma }_{{\beta }_{2j}}^2)$. Note that gender-specific variances are assumed in the distributions of β_lij and β_2ij. These flexible assumptions allow gender-specific effects of histamine and its interaction with T_ij, which were motivated by the findings from our cohort (at age 18, the average histamine wheal size of males is 5.46 cm and of females is 5.09 cm; P-value = 0.00004 based on two-sided two sample t-tests for population means). Finally, ∈_ij explains unknown random effects on O_ij and is assumed to be normally distributed with mean zero and variance ${\sigma }_1^2$.

The true wheal size

The latent variable T_ij in (1) represents wheal sizes in reaction to an allergen (the true wheal size). We model T_ij as $T_{ij}=\mathrm{\Upsilon }+{\delta }_{ij},$(2) in which ϒ denotes what we expect on wheal sizes for a general population in reaction to an allergen, regardless of gender. The second term δ_ij is for random errors. It represents possible differentiated reaction to the allergen at an individual level. We assume δ_ij is half-normally distributed, that is, ${\delta }_{ij}\sim Half-N(0,{\sigma }_2^2),$ where zero and ${\sigma }_2^2$ denote the mean and variance in the corresponding normal distribution function. The density of the half-normal distribution defined above is in a shape of a half bell-curve starting at zero. This distribution function is utilized to reflect the fact that most subjects are non-atopic. Besides the half normal distribution, other skew distributions can be possibly applied, for instance, the skew normal distribution.^16,17

The message conveyed by model (2) is that the wheal sizes of males and females are expected a priori to follow the same distribution. However, if F_ij and ∈_ij in (1) are not sufficient to explain gender discrepancy, the skew-distributed random error δ_ij can still possibly differentiate males’ and females’ true wheal sizes. In this case, data for different genders are likely to be generated from different parts of a half-normal distribution.

The association between eczema and atopy

Since atopy is considered as a risk factor of eczema, modeling the association between true wheal sizes (T_ij) and eczema seems a reasonable instrument in the process of identifying misclassifications. A logistic regression given below is considered: $\text{logit}(P(Y_{ij}=1)|T_{ij})={\eta }_0+{\tau }_j+{\eta }_1{T}_{ij},$(3) where Y_ij takes values 1 or 0 denoting the status of eczema. Equation (3)$\text{logit}(P(Y_{ij}=1)|T_{ij})={\eta }_0+{\tau }_j+{\eta }_1{T}_{ij},$(3) evaluates gender effect τ_j (assuming τ₁ + τ₂ = 0 to avoid singularity) and the effect of true wheal size (η₁) to the odds of eczema.

Statistical analysis

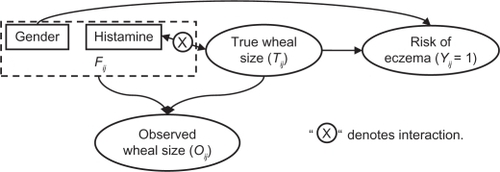
We consider a method of joint modeling to infer the true wheal size. Joint modeling is appropriate for data sharing features in common. It has been used in analysis of combined longitudinal and survival data,^18–20 random effects data,²¹ and mark-recapture data.²² The joint model in our analysis is composed of two parts: the modeling of observed wheal sizes and the modeling of association between the true wheal size and the risk of eczema. The models presented in (1) to (3) are linked to each other with T_ij being the joint. We include a brief structure of the joint model in Figure 1.

Figure 1 Conceptual structure of the joint model.

Note: Squares represent constant (fixed) and ovals represent stochastic variables.

Let f(.) denote a generic density function. Equations (1)$\begin{array}{l}{O}_{ij}=T_{ij}+F_{ij}+{\in }_{ij}\\ F_{ij}={\alpha }_i+{\beta }_{1ij}{H}_{ij}+{\beta }_{2ij}{T}_{ij}\times H_{ij},\end{array}$(1) to (3)$\text{logit}(P(Y_{ij}=1)|T_{ij})={\eta }_0+{\tau }_j+{\eta }_1{T}_{ij},$(3) induce a joint density of Y_ij, O_ij, and T_ij in a hierarchical structure, which is $\begin{array}{lll}f(Y_{ij},O_{ij},T_{ij})\hfill & =\hfill & P(Y_{ij}=1|T_{ij},O_{ij})f(O_{ij}|T_{ij})f(T_{ij})\hfill \\ \hfill & =\hfill & P(Y_{ij}=1|T_{ij})f(O_{ij}|T_{ij})f(T_{ij})\hfill \end{array}$(4)

Here we suppress the dependence on the unknown parameters for simplicity. The last equality is due to the assumption that the observed wheal size does not provide any additional information at the presence of true wheal size (non-differentiable measurement errors). The advantage of a joint analysis is that more sources of information can be incorporated, and thus the inference on true wheal sizes is expected to be more accurate. The joint model presented in (4) allows us to infer T_ij based on information from two sources, the disease status Y_ij and observed wheal size O_ij. Inferences of T_ij will be further used to facilitate the revision of the 3 mm cutoff point.

Let $\theta =\{{\alpha }_j,{\sigma }_{{\beta }_{1j}}^2,{\sigma }_{{\beta }_{2j}}^2,{\sigma }_1^2,{\sigma }_2^2,\gamma ,{\eta }_0,{\eta }_1,{\tau }_j\}$ denote a collection of parameters. The hierarchical structure shown in (4) motivated us to utilize the Bayesian method to infer the parameters and true wheal sizes T_ij. Here we briefly discuss the steps necessary to draw Bayesian inferences. To be fully Bayesian, we assign prior distributions to each parameter. Prior distributions of coefficients including α_j, γ, η₀, η₁ and τ_j are selected as vague normal distributions with mean zero and large variances. Prior distributions of variance components including ${\sigma }_{{\beta }_{1j}}^2$, ${\sigma }_{{\beta }_{2j}}^2$, ${\sigma }_1^2$ and ${\sigma }_2^2$ are assumed to follow inverse gamma distributions with scale and shape parameters being 0.5 and 0.0005, respectively.²³ Once prior distributions are specified, the joint posterior distribution of the parameters can be formulated using equations (1)$\begin{array}{l}{O}_{ij}=T_{ij}+F_{ij}+{\in }_{ij}\\ F_{ij}={\alpha }_i+{\beta }_{1ij}{H}_{ij}+{\beta }_{2ij}{T}_{ij}\times H_{ij},\end{array}$(1) to (4)$\begin{array}{lll}f(Y_{ij},O_{ij},T_{ij})\hfill & =\hfill & P(Y_{ij}=1|T_{ij},O_{ij})f(O_{ij}|T_{ij})f(T_{ij})\hfill \\ \hfill & =\hfill & P(Y_{ij}=1|T_{ij})f(O_{ij}|T_{ij})f(T_{ij})\hfill \end{array}$(4) in a hierarchical way. Next, we use the Markov Chain Monte Carlo (MCMC) approach, specifically, the Gibbs sampler to draw samples for each parameter and T_ij from the joint posterior distribution. The convergence of the MCMC chains is examined using the method proposed in pervious studies.^24–26 The program is coded in WinBUGS.27 A detailed graphical structure with all parameters included are given in the Appendix (Figure 3) along with the corresponding WinBUGS program (Figure 4).

Appendix Figure 1 The detailed structure of the Bayesian joint model.

Appendix Figure 2 The WinBUGS program corresponding model structure in Appendix Figure 1.

Defining adjusting factor F_j and cutoff value $C_j^o$

The proposed approach draws inferences on the true wheal sizes T_ij. In practice, clinicians or epidemiologists may be more interested in handy cutoff values, which is practically more meaningful. Based on posterior inferences of T_ij and F_ij, we propose revised cutoff points $C_j^o$ applied to O_ij for males and females, respectively. The revised cutoff value is defined as $C_j^o=3-{\stackrel{⌢}{F}}_j$ according to (1), j = 1, 2, where the 3 mm is the current cutoff value and F̑_j denotes an estimate of adjusting factor F_j. The adjusting factor can be estimated by taking the means of posterior estimates of F_ij for each gender; recall F_ij in (1) represents an adjustment to each individually observed wheal size. It can also be estimated as the difference between O_j and T̑_j for gender j, where O_j is the mean of observed wheal sizes O_ij, T̑_j is the estimate of mean true wheal size for gender j and is calculated as the sample mean of the inferred true wheal sizes T_ij.

Examining the proposed method

To evaluate the insights brought in by T_ij and $C_j^o$, we examine if the discrepancy is reduced or eliminated between males’ and females’ prevalence in atopy and in eczema among atopic cases. We apply two-sided two sample proportion tests to test the difference between genders of atopy prevalence and of eczema prevalence among atopic cases. We then compare the results from T_ij and $C_j^o$ to those from O_ij and the 3 mm cutoff value. We also evaluate the difference of T_j between genders, and compare it with the difference of O_j between genders. For this purpose, two-sided two sample t-tests applied to population means are applied. For each type of test, the Bonferroni approach is used for multiple testing corrections. The experiment-wise significance level is set at 0.05.

Results

Inferences of T_ij and $C_j^o$

Using the proposed method, we infer T_ij and the adjusting factors for each of the four allergens (HDM, grass pollen, dog dander, and Alternaria). Table 2 includes descriptive statistics (mean and standard deviation) of O_ij and T_ij for each gender, denoted as O_j and T̑_j in the table, respectively. The revised cutoff values $C_j^o$ are presented in the last column of the table. As shown in the table, overall the results are consistent across different allergens for each gender. For females, T̑_j agrees with O_j, and $C_j^o$ agrees with the commonly used 3 mm cutoff point. However, this is not the case for males. For males, T̑_j’s are all smaller than O_j’s and larger cutoff values are suggested.

Table 2 Summary of observed and inferred wheal sizes and proposed cutoff values (The unit of each variable is in millimeters. Standard deviations are in the parentheses)

Gender	Oj	T̂j	F̂j	$C_j^o$
HDM
Males	2.08 (2.78)	1.66 (0.98)	−0.43	3.43
Females	1.36 (2.37)	1.48 (0.97)	0.10	2.90
P-value	0.000065	0.0061
Grass
Males	1.80 (3.03)	1.33 (0.89)	−0.51	3.51
Females	1.23 (2.36)	1.25 (0.86)	0.01	2.99
P-value	0.0023	0.14
Dog dander
Males	0.77 (1.54)	0.59 (0.36)	−0.18	3.18
Females	0.55 (1.27)	0.57 (0.35)	0.02	2.98
P-value	0.021	0.31
Alternaria
Males	0.61 (1.66)	0.39 (0.26)	−0.22	3.22
Females	0.39 (1.31)	0.38 (0.25)	0.01	2.99
P-value	0.036	0.42

Notes: j = 1, 2 denotes two genders. O_j: the average of observed wheal sizes. T̂_j: the average of inferred true wheal sizes. F̂_j: estimate of the adjusting factor $C_j^o$ is the revised cutoff point. Two F sample t-tests were performed to test the differences of means between gender. In columns 2 and 3, respectively, multiple testing adjusted significance level is 0.0125 (0.05/4 = 0.0125) using the Bonferroni method. P-values are listed to show the significance of mean difference of wheal sizes between genders.

By comparing the differences of O_j between genders and the differences of T̑_j between genders, we can see that the adjusting process clearly has the ability to reduce the disagreement of wheal sizes between males and females. In particular, as indicated by the P-values, the disagreement of wheal sizes between gender based on T_ij is eliminated for all allergens except for HDM. The significant differences between genders for HDM implies that besides histamine reactivity effect and its interaction with HDM, other unknown but non-random factors may also contribute to the formation of discrepancy. Further studies are needed to identify those possible factors. On the other hand, as indicated by the reduction of P-values, although gender discrepancy is not eliminated for HDM, the probability of observing such difference between males and females under the null hypothesis is increased compared to that based on O_ij. This implies that on average the dissimilarity between males’ and females’ wheal sizes is reduced based on the inferred true wheal sizes.

The inferences of T_ij discussed so far are promising in that gender discrepancy in wheal sizes is significantly reduced. However, the reduction of disagreement in wheal sizes does not necessarily lead to a discrepancy reduction in the prevalence of sensitization to an allergen. This is examined in the following section.

Prevalence comparison based on T_ij

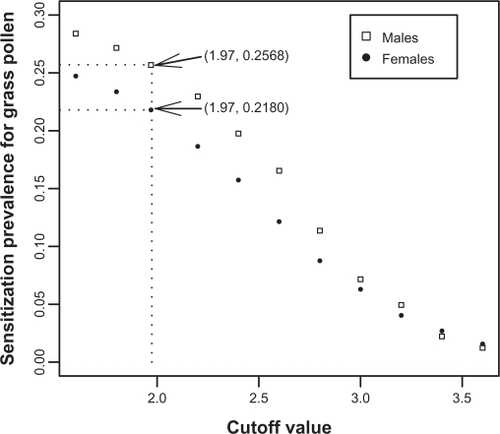
To compare sensitization prevalence between gender using T_ij (true wheal size), a cutoff value $C_j^t$ applied to T_ij is needed. We use inferences related to grass pollen to demonstrate the $C_j^t$ selection process. Figure 2 plots the prevalence of sensitization based on T_ij versus different cutoff values. The difference of prevalence between genders decreases as the cutoff value increases, which implies the importance of choosing an appropriate cutoff value. As indicated in Table 2, the revised cutoff values for females (the last column of Table 2) in general agrees with the commonly applied 3 mm cutoff point. Our paired tests further indicate that T_i1 agrees with O_i1 in all the four allergens (all P-values > 0.05. For this grass pollen example, the P-value is 0.79). These results imply that for females the sensitization prevalence based on O_i1 is expected to agree with the prevalence based on T_i1. As discussed below, this finding is then utilized to determine an atopy cutoff value for T_ij applied to both genders, since there is no significant difference of T_ij between genders.

Figure 2 The relationship between sensitization prevalence of wheat and cutoff value based on T_ij.

The prevalence of atopy for females based on O_ij is 21.34% as in Table 1. Given the agreement between O_i1 and T_i1, we apply this prevalence to T_ij resulting in a cutoff value $C_j^t=1.97\hspace{0.17em}\text{mm}$. Using this cutoff value, the sensitization prevalence for males is 25.68% and for females is 21.80% (different from 21.34% due to rounding errors), which are insignificantly different from each other (P-value = 0.09). The same procedure is repeated for the remaining three allergens. The cutoff values $C_j^t$ and the comparison of sensitization prevalence between genders are summarized in Table 3. After adjusting for multiple testing using the Bonferroni method (multiple testing adjusted significance level = 0.0125), the differences of atopy prevalences between genders are no longer statistically significant for any single allergen. Utilizing information summarized in Table 1, we then identified the individuals, especially males, who are misclassified into the atopic group by applying the 3 mm cutoff to the observed wheal sizes O_ij. Specifically, among 142 males originally classified into the HDM sensitization group, 25 (17.61%) are misclassified; results of misclassification for grass pollen, dog dander, and Alternaria are 4 (3.70%) out of 108, 16 (32%) out of 50, and 14 (35.90%) out of 39, respectively.

Table 3 Cutoff values and sensitization prevalence comparison between gender based on T_ij

Allergen	Cutoff value (mm)	Sensitization prevalence (%)
		Males	Females	P-value
HDM	2.4	28.89	22.92	0.023
Grass	1.97	25.68	21.80	0.09
Dog dander	1.28	8.40	9.21	0.34
Alternaria	0.99	6.17	6.97	0.32

Notes: Two-sided two sample proportion tests are used to test gender differences between percentage for each allergen. Multiple testing adjusted significance level is 0.0125 (0.05/4) using the Bonferroni method. P-values are listed to show the significance of prevalence differences between gender.

So far our focus is on the prevalence of atopy. We now turn to the comparison of eczema prevalence among atopic cases. The results are given in Table 4. Comparing the prevalence differences between genders, we can see that the results of insignificant differences drawn from O_ij (see Table 1) are kept for T_ij. This finding, coupled with the findings on T_ij-based atopy prevalence, demonstrates the applicability of the proposed adjusting process. This process has the potential to correct the bias in wheal size measuring and resolve the conflict between atopy prevalence and findings on eczema prevalence and IgE measures.

Table 4 Eczema cases with positive sensitization based on T_ij

Allergen	% of atopic cases with eczema
	Males	Females	P-value
HDM	16.24 (117)	22.55 (102)	0.12
Grass	13.72 (102)	19.59 (97)	0.13
Dog dander	41.18 (34)	29.26 (41)	0.14
Alternaria	16.00 (25)	19.35 (31)	0.37

Notes: The numbers of positive sensitization are included in the parentheses. Two-sided two sample proportion tests are used to test gender differences between percentage for each allergen. Multiple testing adjusted significance level is 0.0125 (0.05/4) using the Bonferroni method. P-values are listed to show the significance of percentage differences between gender.

In an early section, we proposed cutoff values $C_j^o$ applied to O_ij. Even with the promising gain from inferring T_ij, to clinicians and epidemiologists, it is possibly more convenient to use $C_j^o$. In the next section we examine if we can reach the same conclusion on the elimination of gender discrepancy by using $C_j^o$.

Prevalence comparison based on $C_j^o$

We apply the revised cutoff value $C_j^o$ given in Table 2 to the observed wheal sizes to infer the prevalence of sensitization and that of eczema among atopic cases. The results are presented in Table 5. Compared to the results given in Table 1, the updated prevalence differences between genders for each allergen are less significant, although for HDM the significant gender discrepancy still exists. The prevalence of eczema among atopic cases is not significantly different between males and females for each individual allergen, the same trend as in Table 1.

Table 5 Comparison of prevalence between gender based on $C_j^o$ of sensitization and percentage of atopic cases having eczema

Allergen	Sensitization prevalence (%)			Prevalence of eczema among atopic cases (%)
	Males	Females	P-value	Males	Females	P-value
HDM	32.35	23.37	0.0017	15.27	21.15	0.12
Grass	24.75	21.35	0.12	14.00	18.95	0.18
Dog dander	10.62	8.99	0.21	27.91	25.00	0.38
Alternaria	8.89	6.74	0.12	19.44	20.00	0.47

Notes: Two-sided two sample proportion tests are used to test gender differences between percentages for each allergen. For tests in columns 4 and 7, respectively, multiple testing adjusted significance level is 0.0125 (0.05/4 = 0.0125) using the Bonferroni method. P-values are listed to show the significance of percentage differences between gender.

By using although the gender discrepancy cannot be completely eliminated for all allergens and the results are not as promising as those based on T_ij (Tables 3 and 4), the revised cutoff value $C_j^o$ does have the potential to decrease the significance of gender discrepancy in sensitization prevalence.

Discussion

Motivated by the inconsistency between the wheal size-based atopy prevalence in men and women and the results of IgE measures, we developed a Bayesian method to estimate true wheal sizes and proposed gender-specific sensitization cutoff values for different allergens. The disease outcome considered in this work is eczema. The allergens considered are common aeroallergens including house dust mite, grass pollen, dog dander, and Alternaria.

Based on inferred true wheal sizes (T_ij), the differences in sensitization prevalence between males and females are statistically insignificant with respect to each individual allergen, and the chance that sensitized males developing eczema is comparable to that of sensitized females. This indicates a significant improvement compared to the results based on observed wheal sizes with the 3 mm cutoff. On the other hand, if we apply the revised cutoff values $C_j^o$ to observed wheal sizes (other than directly using inferred T_ij), our results showed limited improvement. It thus seems more reasonable to adjust the observed wheal sizes than to revise the 3 mm cutoff value for each allergen and gender. The findings can be further assessed by calculating the sensitivity and specificity with the help of gold standard such as radioallergosorbent test proposed in early studies.^28,29 We also applied the method to two other allergic diseases, asthma and rhinitis. Similar results are drawn for allergens HDM, grass pollen, and dog dander. For Alternaria, results from the method suggest adjusting wheal sizes is unnecessary.

On the other hand, since utilizing revised cutoff values ($C_j^o$) does reduce the differences between males and females, although the reduction is not significant in some situations, one may wonder the possibility to propose cutoff values separately for males and females but apply to all allergens. We further investigated this possibility. Based on the results given in Table 2, we used 3.5 mm cutoff for males and 3 mm cutoff for females. These cutoff values are applied to all allergens. However, as indicated by the results in Table 6, very limited reduction in the statistical significance is observed. Similar results are obtained when using other cutoff values different from 3.5 mm. This finding indicates that just revising cutoff points applied to all allergens may not at all solve the prevalence discrepancy between males and females. Instead, we may have to deal with each individual allergen.

Table 6 Comparison of prevalence between gender of atopy and percentage of atopic cases having eczema based on different cutoffs on all allergens

Allergen	Sensitization prevalence (%)			Prevalence of eczema among atopic cases (%)
	Males	Females	P-value	Males	Females	P-value
3 mm (males and females)	47.89	35.36	0.00011	11.92	20.38	0.00010
3.5 mm (males), 3 mm (females)	45.91	35.36	0.00089	11.89	20.38	0.00023

Notes: Two-sided two sample proportion tests are used to test gender differences between percentages for each allergen. For tests in columns 4 and 7, respectively, multiple testing adjusted significance level is 0.0125 (0.05/4 = 0.0125) using the Bonferroni method. P-values are listed to show the significance of percentage differences between gender.

Conclusion

To correct misclassified atopic cases caused by gender discrepancy, we can utilize the proposed statistical methods to adjust wheal size measures. Besides adjusting observed wheal sizes, we found that using allergen-specific cutoff values different for men and women ($C_j^o$) will also reduce the occurrence of misclassifications.

Clinicians may prefer the same cutoff value applied to all allergens. To achieve this goal and keep misclassification reduced, a laboratory-related alternative solution may be possible. Specifically, based on the inferred cutoff values $C_j^o$, one can adjust the concentration of allergens used in the prick test solutions for men and women, respectively. The results from this work may assist the determination of allergen concentration. This approach makes it possible to reduce the gender discrepancy in atopy without revising cutoff values. Our work shows that future clinical, mechanistic, and epidemiological studies are needed to optimize the skin prick test to make it agree with results from specific IgE levels.

Acknowledgements

This work was supported by the National Heart, Lung, and Blood Institute at the National Institute of Health (5R01 HL082925, PI: Arshad SH; 1R03HL095429, MPI: Zhang H).

Disclosure

The authors report no conflict of interest in this work.

Appendix

The model structure

The structure in Figure 1 shows the formulation of the Bayesian joint model including models (1) to (3) along with the specified prior distributions. It is drawn using DoodleBUGS.²⁹ Squares represent constant (fixed), ovals represent stochastic or unknown variables, hollow (thicker) arrows are for logical functions (such as definitions or identities), and single arrows are for stochastic dependencies (distributions involved). There are two panels in the figure. The smaller panel indicated by “for (i IN 1:n[j])” is for parameters and random variables related to each individual, the ovals between the bigger panel and the smaller one are for the parameters exclusively related to gender, and the ovals outside the two panels are for common parameters.

The WinBUGS codes

The codes below are consistent with the structure given in Figure 1.