Acoustic cardiac signals analysis: a Kalman filter–based approach

Abstract

Auscultation of the heart is accompanied by both electrical activity and sound. Heart auscultation provides clues to diagnose many cardiac abnormalities. Unfortunately, detection of relevant symptoms and diagnosis based on heart sound through a stethoscope is difficult. The reason GPs find this difficult is that the heart sounds are of short duration and separated from one another by less than 30 ms. In addition, the cost of false positives constitutes wasted time and emotional anxiety for both patient and GP. Many heart diseases cause changes in heart sound, waveform, and additional murmurs before other signs and symptoms appear. Heart-sound auscultation is the primary test conducted by GPs. These sounds are generated primarily by turbulent flow of blood in the heart. Analysis of heart sounds requires a quiet environment with minimum ambient noise. In order to address such issues, the technique of denoising and estimating the biomedical heart signal is proposed in this investigation. Normally, the performance of the filter naturally depends on prior information related to the statistical properties of the signal and the background noise. This paper proposes Kalman filtering for denoising statistical heart sound. The cycles of heart sounds are certain to follow first-order Gauss–Markov process. These cycles are observed with additional noise for the given measurement. The model is formulated into state-space form to enable use of a Kalman filter to estimate the clean cycles of heart sounds. The estimates obtained by Kalman filtering are optimal in mean squared sense.

Keywords:

• heart sound
• murmurs
• ECG
• Kalman filters
• acoustic cardiac signals

Introduction

The heart is divided into four chambers. The upper chambers are called atria and lower chambers are called ventricles. The heart muscles squeeze blood from chamber to chamber. At each squeeze, the valve opens to let blood move backward. In this way, the valve keeps blood moving as efficiently as possible through the heart and out to the body.¹ Heart sounds result from the interplay of dynamic events associated with the contraction and relaxation of the atria’s and ventricles’ valve movements and blood flow. The heart can emit normal heart sounds or murmurs. The positioning of the stethoscope at the auscultatory area plays a significant role in diagnosis of heart murmurs.

Nanomedicine is an emerging field, with nanotechnology concepts for diagnosis and treatment of cardiovascular disease.² Heart-sound data depend on the electronic stethoscope, which is bulky, and the mechanism to extract the data depends on the movement of the diaphragm of the heart. The oscillations of the diaphragm are converted to the heart-sound signal, and this approach is sensitive to artifacts and external noise. There is a possibility that the use of nanomedicine also involves applications of nanoparticles or nanoneedles, both of which are currently under development and could completely change the way physicians detect and treat cardiac patients. For example, in nanomedicine, iron oxide nanoparticles can be used to improve magnetic resonance imaging of cancer tumor. Peptide-coated nanoparticles can bind to a cancer tumor; once the nanoparticles are attached to the tumor, the magnetic property of the iron oxide enhances the images from a magnetic resonance imaging scan. In related work,^3,4 characterization of cellular mechanics of cast cells was carried out using nanoneedles inside an environmental scanning electron microscope. The nanoneedles are used to measure local stiffness characteristics of single cells. Important in estimating the stiffness of the cell is choosing the correct tip geometry, such as conical, spherical, or cylindrical. Two important steps have to be carried out before nanoneedles are used to measure cell stiffness: fabrication of soft and hard nanoneedles, and calibration of soft nanoneedles.^5,6 In related work, a finite element method–code Abaqus was used for numerical analysis to ensure that only good-quality nanoneedles were selected for measurement of reliable data. In this research,³ it was possible to detect defective nanoneedles, which should not be used to measure stiffness variation among single cells. This work is important; previous work did not use finite element method analysis during calibration of the soft nanoneedle. The above research clearly indicates the possibility of designing better and less bulky sensors to measure heart sounds. The Center for Biomedical Engineering is currently pursuing the idea of beam deformation using piezoresistance as a measure of heart murmurs.

Auscultation area

Auscultation sites may vary according to the patient’s anatomy. In studying heart sound, emphasis should be placed on its intensity (faint/moderate/loud), which greatly depends on the location of the stethoscope on the precordium (skin). Those who intend to study heart auscultation should consult the experts (cardiologists) regarding correct positioning of the stethoscope. Auscultation of the heart should take place in a quiet room, with the patient’s chest exposed if necessary. The stethoscope should be equipped with a stiff diaphragm and shallow bell. The principal area of interest is shown in Figure 1. As an example, placing the stethoscope at the semilunar valve (aortic and pulmonary) provides better S₂ sound. The S₁ heart sound can be heard more clearly in the atrioventricular (AV) area known as the AV valve.

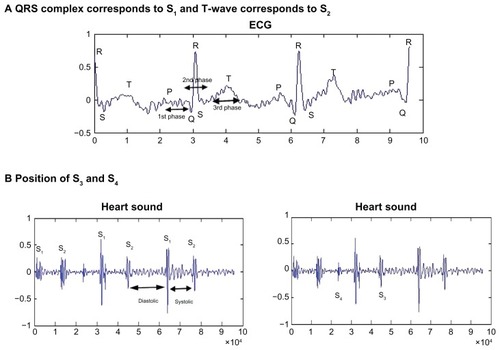
Figure 1 Auscultation area: listening positions for S₁, S₂, S₃, and S₄ heart sounds. (A) QRS complex corresponds to S₁, and T-wave corresponds to S₂. (B) Position of S₃ and S₄.

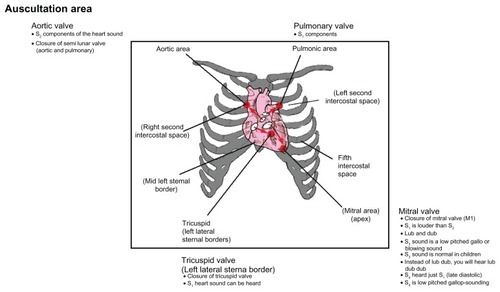
Figure 1 shows stethoscope positions to listen to normal S₁, S₂, S₃, and S₄ sounds. The intensity of S₁ depends on the rate of pressure development in the ventricle, the structure of the valve leaflets, and the position of the AV valves at the beginning of the ventricle contraction. The goal is to listen to the four areas corresponding to the valves, which provide valuable information to GPs and can be a very valuable diagnostic tool to examine the hearts of patients. If the stethoscope is placed at the apex (mitral valve), the normal “lub dub” sounds can be heard during the closure of this valve. The S₂ sound corresponds to the closure of the aortic and pulmonary valves. At the mitral valve (apex), the S₃ sound, as shown in Figure 2C, can be heard as a low-pitched or blowing sound during the mid-diastolic stage. In the same position, S₄ can be heard just before S₁ during the late-diastolic stage as a low-pitched gallop sound. S₃ can be normal for children, while S₄ is not normally present in healthy persons.¹ Normally, the S₁ sound is louder than S₂ at the base of the heart. In certain conditions, S₁ can decrease in intensity when S₂ is louder than S₁ at the cardiac apex.⁷ This happens in states of impaired ventricular contractibility and decreased myocardial tension development, which is known as congestive heart failure. Another factor can be mitral valve immobility. This occurs in severe cases of mitral stenosis. In normal conditions, S₂ is produced by the closure of the aortic and pulmonary valves. S₂ is higher-pitched and shorter in duration than S₁. In this case, S₂ is louder than S₁ at the cardiac base (second intercostal space, as in Figure 1). This is associated with the closure of the aortic valve A₁ and followed by closure of the pulmonic valve P₂.

Figure 2 (A and B) Relationship of ECG and the four heart sounds.

Abbreviation: ECG, electrocardiogram.

Denoising of heart sound

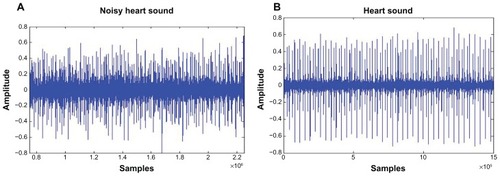
The simplest model for any biomedical signal is the summing of an invariant signal and random noise. A common method to measure these parameters is the averaging technique, which may be reasonable for one type of signal but not for all cases. Figure 3A shows heart-sound signal with some interference such as background noise and artifacts, and Figure 3B shows normal heart-sound signal. The characteristics of heart sound can be faint, moderate, or loud, and the intensity does seriously affect the trial case. The use of average statistics may not be suitable for this case, as they can distort the information. The stethoscope can detect high-frequency sounds, such as systolic murmurs, and detect low-frequency sounds, such as S₃ and S₄. Analyzing such data requires a quiet environment with minimum ambient noise. A heart murmur is defined according to its intensity, frequency, quality, configuration, duration, and radiation.

Figure 3 (A and B) Average signal of normal patient. (A) Noisy heart signal; (B) clean heart signal.

Normally, the performance of the filter naturally depends on prior information related to the statistical properties of the signal and the background noise. Digital filters such as finite impulse response filters are time-invariant and have the drawback whereby the spectrum of the biomedical signals overlaps with the background noise. In a related area of signal processing,⁸ Wiener filters are another denoising approach with a specific filter structure that provides optimal filtering in the mean-squared error sense. The drawback of this approach is that if the signal is time-frequency variable and the assumption mode based on stationary process, then they do not give optimal results. One solution to the denoising problem is the use of the Kalman filter (KF). It provides a mean-squared value that can minimize the error. The KF supports estimates of past, present, and even future states, even when the precise nature of the modeled system is unknown.

On the other hand,⁹ a single-trial dynamical estimation is also used for event-related potentials (ERP). This is based on recursive Bayesian mean-square estimation, which in turn is based on the KF procedure. This proposed method gives excellent estimates for single trials. The design filters give reasonable estimates, even with poor signal-to-noise ratio (SNR). The Bayesian aspects of the method are another benefit of the KF, and it allows a feasible modeling of prior knowledge about the parameters. There are limited applications of using the KF for denoising of the hybrid spatial spectra. To the best of our knowledge, there are no studies on this filter for HSS. In this study, for every cycle of HSS, the KF is applied for denoising to recover a cleaner estimation of the signal. The recursive mean-square estimate for the state is given by KF.

Methods

The signal analysis framework used in this study is illustrated in Figure 4. HSS and the electrocardiogram (ECG) signals were identified and extracted from the acquired data. As mentioned before, auscultations of the heart provide clues to the diagnosis of many cardiac abnormalities. Thus, a heart-sound database is important in the development of an automatic heart diagnosis system. The database can be used in clinical work, research, and teaching of cardiac auscultation. The heart sounds were transduced using phonocardiography sensors and amplified with a preprocessing circuit. These signals were then digitized and stored. However, during collection of data, it was ensured that the data were not corrupted with unwanted noise or artifacts that would affect the performance of the system.

Figure 4 Processing of the HSS and ECG signals.

Abbreviations: HSS, hybrid spatial spectra; ECG, electrocardiogram.

Even though the data were collected in a controlled environment under normal clinical conditions, it was still difficult to collect data free from all the above problems. The heart signals were recorded using a Welch Allyn (Skaneateles, NY) Meditron Electronic stethoscope placed on the chest of the patient. There were ten sets (five normal and five abnormal) of data collected at Fakulti Perubatan, Universiti Teknologi MARA, Kampus Selayang, Hospital Selayang. Each patient’s sound samples were recorded for a duration of 1 minute. Table 1 shows the different number of cycles collected over the different patients. The average number of cycles for the ten patients was 159. Patients with mild murmurs were grouped with the normal subjects. The need for computer-aided auscultation of the heart and for having a standard clinical practice for the recording of heart sounds are discussed in this investigation. Currently, there is no widely available large-scale database for development, evaluation purpose, and comparison of ECG and HSS algorithm. In addressing these issues, the standard practice carried out in this research was as follows: (1) in detecting heart murmurs, there are variations in the placement of the stethoscope, though for general examinations the standard location provides a useful reference point; (2) data collected must be under realistic conditions; and (3) preprocessing done to remove motion artifacts, breath noise, and background noise.

Table 1 Types of murmurs and number of cycles of heart sound per patient

	Patient 3	Patient 1	Patient 5	Patient 4	Patient 2
Name	Mitral valve prolapsed and lateral wall well. Asymptomatic, no heart failure symptoms. Late systolic murmur apex	Moderate mitral regurgitation. Extensive anteroseptal wall and anterolatera. Severe hypokinetic and akinectic indicating ischemic myocardium. Impaired systolic LV function, EF 28%. LA dilatation	Infracted area noted but no scar tissue. LV systolic function slightly depressed but no elevation of PCWP. No thrombus detected. Diastolic dyfunction grade 2	Tricuspid regurgitation. Systolic murmurs	Mitral regurgitation
Number of cycle	74	110	58	88	84
	Patient 10	Patient 6	Patient 9	Patient 8	Patient 7
	Normal, but mild murmurs	Normal	Normal	Normal, but mild murmur	Normal, but mild murmur
	88	70	75	80	80

Abbreviations: LV, left ventricular; EF, ejection fraction; LA, left atrium; PCWP, pulmonary capillary wedge pressure.

The collected sample of the heart sound can be corrupted by sudden movement of the stethoscope and from background noise such as conversation, as in Figure 3A. KF can be used to estimate the underlying nonstationary process for given observation in a minimum mean-squared error sense. This type of filter can be used in many applications^10–12 and has proven to be a powerful filter. The region of electromagnetic spectrum whereof biomedical signals overlaps with background noise have been described in an earlier section. The next section address the use of the KF to estimate the underlying nonstationary process.

As disease cells show different cell mechanical properties as compared to normal cells, fast disease detection is required. A number of researchers are working on cell attachment to substrate in order to understand the sticky force and the surface of substrate. It has been observed that if the sticky force is strong, the cell is healthy, and for weak sticky force the cell is damaged.¹² The current work measured the beam deformation using piezoresistance of a single cell. We believe a similar approach can be used to measure vibration of heart sound from the surface of the skin.

State-space formulation and KF

This paper applied the state-space formulation originally proposed by Shindle⁷ for ERP estimation of heart-sound denoising.

$Let\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{y}_{1:t_t}=\left\{y_1,y_2,\dots \dots \dots \dots \mathrm{..}{y}_t\right\}$(1)

y _{1 : tt} denotes sequence of single cycle of heart-sound signal.

The M signal measurement at the t-trial cycle is represented as a column vector y_t,

$y_t=\left[\begin{array}{c}y\\ ⋮\\ y_t\end{array}\right]$(2)

if we assume θ_t is the denoised version of y_t, which is hidden behind the background noise V_t and is to be estimated by KF. The observation equation of the signal is given by

$y_t={\theta }_t+V_t$(3)

where V_t is the independent and identical distribution (IID) Gaussian noise with zero mean and covariance V_t~IID N (O, R).

The dynamics of θ_t represent cycle-to-cycle variations that are assumed to follow first-order Gauss–Markov process, as shown in equation 3$y_t={\theta }_t+V_t$(3) .

${\theta }_t={\theta }_{{\zeta }^{t-1}}+W_t$(4)

where W_t~IID N(O, Q).

The observation noise covariance, R, and state noise covariance, Q, are assumed to be diagonal with identical values, ie, R =σ_v²I and Q= σ_w²I.

All the model parameters are denoted by

$\theta =\left\{{\sigma }_v^2,{\sigma }_w^2\right\}$(5)

The measurement sequence y_t = T, and if $\widehat{{\theta }_{t|t}}-1$ and $P_{\frac{t}{t}-1}$ are the mean and covariance, respectively, representing one-step-ahead prediction density, and $\widehat{{\theta }_{t|t}}$ and $P_{\frac{t}{t}}$ are the mean and covariance of the filtered density P y (θ | _1:t). The objective is to uncover the underlying clean cycle of heart sounds given the noise measurement; this can be obtained by estimating the filtered distribution of state θ_t given observation Y_1:tY, P(θ_t|y_1:t), using KF.

First, we initiate $\widehat{{\theta }_{o|o}}=0$ and $\widehat{P_{o|o}}=1$.

By denoting (θ_t|t|P_t|t) and ($\widehat{{\theta }_{t|t-t}}|P_{t|t-1}$).

The mean and covariance filtering distribution, prediction distribution are described as respectively follows. The KF algorithm can be summarized as

For t = 1:T

Prediction step

$\widehat{{\theta }_{t|t-1,}}=\widehat{{\theta }_{t-1|t-1,}}$(6)

$\widehat{P_{t|t-1}}=\widehat{P_{t|t-1}}+Q$(7)

Computer Kalman gain

$K_1=\left(P_{t|t-1}+R\right)-1$(8)

Correction step

${\theta }_{t|t}=\widehat{{\theta }_{t|t-t,}}+K_t(Y_t-\widehat{{\theta }_{t|t-t,}})$(9)

$P_{t|t}={\left(1-k_t\right)}_{P_{t|t}}$(10)

Prediction error and prediction error covariance.

The prediction error can be as

$e_t=y_t-\widehat{{\theta }_{t|t-1,}}$(11)

and the prediction error covariance as

$P_{et}=(P_{t|t-1}+R)$(12)

In this paper, instead of using measurement samples for y_t, we use its wavelet coefficients, wherein the dimension of the state vector is greatly reduced, and hence the computational effort. The noisy heart-sound measurements, y_t, are first transformed into a vector of wavelet coefficients before estimation of the θ_t, which is its denoised version. The estimation θ_t is used to reconstruct the clean heart-sound signal. This method has been used^10,11 for ERP estimation using particle filtering. Discrete wavelet transformation of biorthogonal 5.5 is used with an approximation coefficient of level −2.

Results and discussion

Effect of varying noise variance

In this section, the effects of variation in the parameters σ _v² and σ_w² and comparison of these signals between normal and abnormal heart sound are studied. Selection of the optimal valves for noise variances σ_v² and σ_w² is important for KF. The ability to track the change of the state parameters is related to the ratio of state noise to observed variance σ_w². A large value of noise is estimated at a stationary point, while small valves are unable to follow the abrupt changes and suffer a tracking lag.

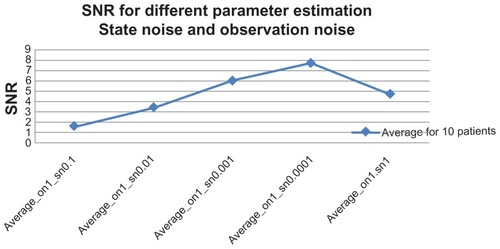
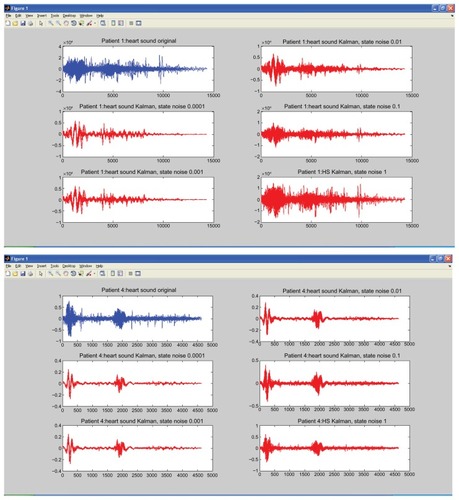
We fixed σ_v² = 1, and allowed observation noise σ_w² to change. The selection of optimal parameters involved only σ_v². Figure 6A shows a patient with murmurs, while 6B shows a normal healthy person. In this experiment, σ_v² was kept constant, and σ_w² was varied, with values of 0.0001, 0.001, 0.01, 0.1, and 1.0. The figure clearly shows that as the value of σ_w² gets bigger, the amplitude of the signals gets smaller, significant levels of the noise are removed, and a clear estimate of the underlying clean heart sound can be obtained. SNR is measured to compare the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise.

To quantify the estimation performance, we used SNR for heart sound, defined as follows

$\text{SNR}=10\hspace{0.17em}{\text{log}}_{10}\frac{{\sigma }_s^2}{{\sigma }_N^2}$(13)

where σ_N² and σ_S² are the noise and signal power estimated using averages over trial as

${\widehat{\sigma }}_N^2=1/[K(J-1)]\sum _{n=1}^J\sum _{k=1}^K{(y_{nk}-{\overline{y}}_k)}^2$(14)

${\widehat{\sigma }}_S^2=1/[K(J-1)]\sum _{K=1}^{K-2}{y}_K\hspace{0.17em}({\widehat{\sigma }}_N^2/J)$(15)

where ${\overline{y}}_k=(1/J){\sum }_{n=1}^J{y}_{nk}$ is the ensemble average of trials.

The goal of this study was to maximize the SNR so that accurate conclusions could be drawn. The experiment was carried out in order to obtain a good quality of heart-sound signal. Actual implementation of the system in a hospital may be met with a noisy environment. The patient may move during recording, causing impulse-like noise in the recorded heart sound due to friction between the stethoscope’s chest piece and the patient’s chest. In this experiment, the robustness of the system against noise was tested. Table 2 shows SNR average over ten patients. The best performance was with σ_w² = 0.0001, where SNR (decibels [dB]) gave a value of 10.3, and the worst value came from σ_w² = 1.0 with SNR = 1.1 (dB) for normal. The SNR with abnormal patients provided the best results, with values of 5.4 and 0.3, respectively, with σ_w² = 0.0001. Figure 5 shows the overall average result of the SNR with different variations over the ten patients.

Table 2 Normal and abnormal patients’ signal-to-noise ratio (SNR)

Figure 5 Overall average signal-to-noise ratio (SNR) of the ten patients.

The goal of this research was to improve the quality and maximize the SNR for the respective heart sounds. Figure 6A shows the SNR of the original noisy heart-sound cycles and after the KF process. The SNR cycles after the KF show significant improvement over the original noisy cycles, which shows a significant reduction in noise. Figure 6B shows less turbulence for normal heart sound (rise and fall) at the systolic and diastolic areas, while 6A shows high turbulence for abnormal heart sound in these areas. Heart murmurs are related to valvular heart disease and typically diagnosed by examining the spectral characteristics of the heart sound with additional information such as amplitude and timing. The preprocessing of this filtered signal plays a significant role before any features can be extracted from the signal.

Figure 6 (A) Abnormal heart sound from a patient after the filtering process; (B) normal heart sound from a patient after the filtering process.

Conclusion

This work addressed the need for a framework that provides tools to automatically segment heart sounds into individual cardiac cycles. The relative contribution of each analytical stage to identify murmurs has been evaluated. Since heart murmurs can be systolic, diastolic, or continuous, they are accompanied by different intensity grades. Some systolic murmurs have proven to be clinically innocent, while all the diastolic and continuous murmurs are classified as abnormal.^6,13–15 The KF is proposed as a preprocessed signal to evaluate system performance based on mel-frequency cepstral coefficients and Gaussian mixture model classifiers. Accessing a heart-murmur analysis system is complicated in terms of its effect on the preprocessing stage, feature extraction, and classification of the heart. First, the types of features used in this area to analyze the acoustic cardiac signals are extensive and followed by performance measures on the classification scheme. Normally, the raw data, y_t, of the heart murmurs depends on θ_t, the denoted version of V_t, which is hidden behind the background noise. In this research, an estimation has been used to reconstruct the clean heart sound and to improve the quality, with a view to maximizing the SNR of the heart-sound signals.

Acknowledgments

We would like to thank the Centre of Biomedical Engineering, University Technology Malaysia research grant (GUP-flagship Q.J130000.2436.00G31), the Institute of Advanced Photonic Science, and the Ministry of Higher Education research grant to support this research. We are also thankful to the King Mongkut Institute of Technology, Thailand, for providing the research facilities.

Disclosure

The authors report no conflicts of interest in this work.