Abstract
Predominately, the intended purpose of a new marker is to augment currently available knowledge about a disease process. That is, by combining the marker with existing knowledge, the researcher hopes to obtain a more accurate estimate of a patient's risk for a certain outcome. This estimate is a measure of absolute risk; for example, if the outcome is binary (such as whether or not metastatic disease is present within 5 years after tumor resection surgery), the absolute risk for a given patient would be the estimated probability of the outcome. Rather than evaluate the performance of absolute risk measures such as this, many marker studies unfortunately focus on measures of relative risk within a sample of patients. Examples of these relative measures include odds ratios for binary outcomes, hazard ratios for time-to-event outcomes, and differences in means for continuous outcomes.
Introduction
Other ill-advised research hypotheses involving the new marker are also commonly employed. First, whether or not the new marker predicts the outcome better than an established marker is not relevant since the goal is not to replace the established marker. Second, comparing markers on statistical significance has no bearing on the accuracy with which the markers in question can collaboratively predict the outcome. Finally, many studies seek to identify among a set of markers those which are prognostic for the disease; this determination in and of itself again does not address the issue of how useful the markers are for providing prognosis. These and other related shortcomings are detailed in Kattan (2004) [Citation1].
Instead of these approaches to evaluating a new marker, the proper underlying question involves determining the predictive contribution of the new marker. Specifically, by how much is predictive accuracy for future patients improved when using the best possible statistical model involving the new marker to predict the outcome, as compared to the best available statistical model not involving the new marker? The goal of this article is to break down the details of this question. In the process, we will describe some recent advances in statistical methodology. We note here that since we are describing an entire area of research in the field of statistics, the depictions that follow are meant to be an overview.
Selection of models for comparison
The question above implies the existence of a published model using established markers; should such a model not exist, the researcher must gather the markers shown or believed to be related to the outcome (within the context of the disease process in question) and build a model on their own. Even in the presence of a published model, this model may be optionally developed with the intention of increasing predictive accuracy with available markers. In this case, each of the three models (the published model, the newly-developed model using the established markers, and a model incorporating the new marker) should all be compared on predictive accuracy.
Techniques for developing prognostic models (e.g., multivariable regression, classification and regression trees and model averaging) are plentiful. It is advisable to try a few techniques since model performance for a given set of predictors can vary based on the type of model employed. In the case that the researcher is establishing a model involving pre-existing markers, the same techniques should be attempted for both models to avoid bias.
Evaluating prediction model performance
Predictive accuracy of a model is characterized by two fundamental principles: discrimination and calibration. Discrimination is defined as the model's ability to separate outcomes, while calibration refers to the agreement between the model's predicted values and the observed outcomes (usually as a function of the predicted values). We focus on the evaluation of predictive accuracy for models with binary endpoints, though much of the methodology below has been derived from or extended to scenarios involving other types of outcomes.
Whether or not a model is accurate for the data on which it was developed (which we call the training cohort) is much less relevant than whether or not it can accurately predict outcome for newly-acquired data (validation cohort). For example, a model that is complex enough can perfectly discriminate between events and non-events in the training cohort but will quite likely show poor discrimination for new data; this phenomenon is called over-fitting (incidentally, a general technique known as shrinkage or penalization can be employed during model estimation in order to reduce the amount of over-fitting). It is because of this potential over-fitting that, preferably, discrimination and calibration are assessed within a validation cohort (either reserved from the original sample or collected at a later time). However, in situations where the number of patients in the entire cohort is small, cross-validation [Citation2,Citation3] and bootstrap resampling [Citation4,Citation5] techniques can be employed to avoid over-fitting.
In the binary context, discrimination refers to the model's ability to separate events from non-events. A straightforward method for evaluating discrimination is to determine the absolute difference in mean predicted probability between patients with and without the event. This quantity is known as the discrimination slope [Citation6], and larger values of the discrimination slope imply greater discriminative power of the model.
Graphically, discrimination can be evaluated in at least two ways. First, one may create histograms of the predicted probability of the outcome by observed outcome (i.e., one for patients experiencing the outcome and for patients not experiencing the outcome). A model exhibiting little discriminative ability will result in largely overlapping histograms, while a highly-discriminative model will result in divergent histograms. A second graphical depiction of discrimination is the receiver operating characteristic (ROC) curve, which plots model sensitivity vs. (1-specificity). Based on this relationship, a widely-used measure of discrimination is the area under the ROC curve, which is also known as the concordance index or C-statistic [Citation7]. The concordance index ranges between 0.5 and 1.0, where a value of 0.5 represents no discriminative ability of the model (beyond that of random guessing) and a value of 1.0 represents perfect discrimination.
A new marker, when used in conjunction with established markers, should significantly increase the concordance index over that achievable when using only the established markers. This difference in concordance indexes is perhaps the most important measure of value to be associated with the new marker. A null hypothesis of no difference in concordance index between models can be tested – and corresponding confidence interval estimates of the difference can be obtained – by using bootstrap resampling techniques.
An omnibus assessment of calibration of a model, called calibration-in-the-large, is to compare the average predicted probability of outcome with the proportion of patients experiencing the outcome within a validation cohort. If the training cohort was healthier or sicker than the general population, this form of bias may be present. In addition to evaluating calibration-in-the-large, the prognostic model should calibrate well with respect to individual predictions; that is, among (validation cohort) patients with X% predicted probability of the outcome, which proportion actually experience the outcome? This type of calibration is a function of the predicted probability; if the observed proportion is close to the predicted probability over the entire range of predicted probabilities, then the model is well-calibrated.
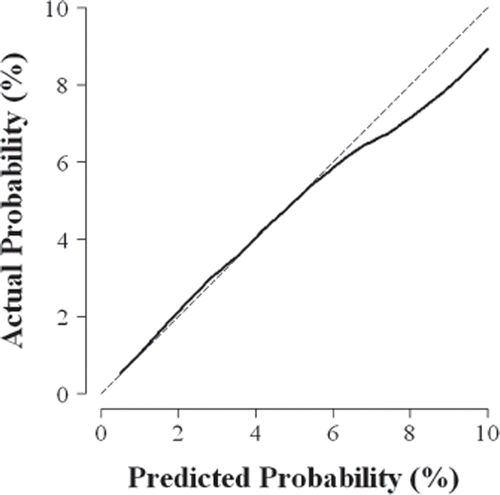
A graphical method for evaluating model calibration is to use smoothing to estimate the relationship between the observed outcomes (y = 0 or 1 for a binary endpoint) and the predicted probabilities (x ranges from 0 to 1). Well-calibrated models will produce smoothed estimates of the relationship that lie on the 45 ° line through the origin (y = x, ). When the smooth curve displays evidence of predicted probabilities too low for those with low risk of the outcome and too high for those with high risk of the outcome (i.e., a relationship generally flatter than 45 °), there is evidence of over-fitting to the training cohort [Citation8].
A popular global test for calibration is the Hosmer-Lemeshow (H-L) chi-squared test [Citation9]; this test is based on partitioning the validation cohort into approximately 10 equally-sized groups according to their predicted probabilities for the outcome and comparing the within-group average predicted probability to the observed within-group proportion of events. A variant of this test is to use clinically appropriate cut-points (defined a priori) to define the groups for the test (for instance, <1%, 1–5%, 5–10%, 10–20%, and ≥20%). In either case, a fundamental issue arises with the H-L test in that the statistical significance of the test depends on the choice of cut-points. To remedy this issue, a smoothing-based goodness-of-fit test for binary regression models has been introduced by le Cessie and van Houwelingen (1991) [Citation10].
Similar to using the difference in concordance indexes as a measure of change in discriminative ability between a model with the established markers alone and a model with both the established markers and the new marker, the two models can be compared on calibration using the relatively new concept of reclassification. By using the model involving the new marker, the proportion of true positives should be increased, as well as the proportion of true negatives (correspondingly, false positive and false negative proportions are decreased). If the predicted probabilities are grouped into clinically-appropriate categories for the disease (as exemplified above), the proportion of patients correctly reclassified – reclassification into a greater risk category for those with the outcome and reclassification into a lesser risk category for those without the outcome – can be characterized by a measure called the Net Reclassification Improvement (NRI) [Citation11]. However, the same discretization issue arises as with the H-L test; NRI is dependent on the selection of cut-points. Consequently, an analogous measure to the NRI which doesn't require cut-points (called the Integrated Discrimination Improvement, or IDI) alleviates this issue [Citation11]. As it happens, the IDI is equal to the difference in discrimination slopes of the two models.
Figure 1. Example of a calibration plot for a clinical prediction model. Smooth regression is used to characterize the relationship between the probability of the outcome predicted by the model and the actual proportion of patients who experience the outcome. If the smooth relationship (solid line) lies on the 45° line through the origin (y = x, dashed line), then the model is well-calibrated. In this example, the clinical prediction model over-estimates risk for patients whose predicted probability of the outcome is greater than 6%.
Other issues
We have discussed methods for developing and validating clinical prediction models, as well as methods for comparing the best possible prediction model involving previously-established markers to the best possible prediction model incorporating the new marker (in addition to the previously-established markers). But just what is meant by a “best possible” prediction model? Arguably, the highest priority in model development is to maximize measures of discrimination. As is often the case, many modelling options produce comparable discrimination measures (for a given set of markers), in which case the model producing the best evidence of calibration should be chosen.
The validation cohort we described above is in practice either a random sample or a consecutive sample of the most recent patients in the cohort available at the time of the analysis. While good model performance on this type of validation cohort is necessary evidence for proving the usefulness of a new marker, it does not suffice for commencing with its use in clinical practice. Rather, the same type of model performance must be shown on at least one (but preferably more) externally-collected samples. That said, it can be argued that the stringency of this requirement diminishes with larger samples from more representative patient populations (such as national organ donor registries).
Finally, even if the new marker is shown to improve performance of a clinical prediction model, the clinical community must address whether or not the gain in prognostic performance is worth the cost of collecting data on the new marker.
Conclusion
We provided a general overview of current methods for evaluating the prognostic importance of a new marker, with respect to characterizing the future course of a disease. This methodology focuses on the ability of the marker to augment currently available knowledge about the future value of a clinical endpoint. Specifically, we overviewed methods of measuring the change in discriminative ability and the change in calibration introduced by adding the marker to the pool of predictor variables in a statistical model. Only after the researcher is able to show that the incorporation of the new marker leads to prospective and cost-effective improvements in either or both of these aspects of predictive accuracy can it be argued that its collection is warranted for more precise assessments of patient prognosis.
Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.
References
- Kattan MW. Evaluating a new marker’s predictive contribution. Clin Cancer Res 2004;10(3):822–4.
- Efron B. Estimating the error rate of a prediction rule: Improvement on cross-validation. J Am Stat Assoc 1983;78: 316–31.
- Van Houwelingen JC, Le Cessie S. Predictive value of statistical models. Stat Med 1990;9:1303–25.
- Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat Sci 1986;1:54–75.
- Efron B, Tibshirani R. An introduction to the bootstrap. New York, Chapman & Hall, 1993.
- Yates JF. External Correspondence – Decompositions of the mean probability score. Org Behav Hum Perform 1982; 30(1):132–56.
- Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982;143(1):29–36.
- Harrell FE. Regression modeling strategies: with applications to linear models, logistic regression, and survival analysis. Springer series in statistics. New York: Springer, xxii, 2001568.
- Hosmer DW, Lemeshow S. Applied logistic regression. 2nd. Wiley series in probability and statistics. Texts and references section. New York: Wiley. xii, 2000375.
- Le Cessie S, van Houwelingen JC. A goodness-of-fit test for binary regression models, based on smoothing methods. Biometrics 1991:47(4):1267–82.
- Pencina MJ, D'Agostino RB Sr, D'Agostino RB Jr, Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med 2008;27(2):157–72.