Treatment of leg veins with indocyanine green and lasers investigated with mathematical modelling

Abstract

Purpose: The treatment of leg veins is routinely performed in clinical practice using near infrared (NIR) lasers. However, due to low absorption of NIR light in blood vessels, the clinical results are still suboptimal. The absorption of the NIR light can be significantly increased with intravenous introduction of an indocyanine green (ICG) dye. In this work a mathematical model was used to delineate clinically valid settings for ICG and NIR lasers for the treatment of leg veins.

Methods: A finite element commercial package was used to simulate light propagation and absorption and heat generation in a skin-like geometry. The simulations were conducted for 755 nm and 810 nm light wavelengths, which are emitted by alexandrite and diode lasers, respectively. Five different laser settings, six different vessel diameters (0.1-2 mm) and three ICG concentrations (0, 1 or 2 mg/kg body weight (BW)) were used to calculate the temperature field spatial distribution as a function of time.

Results: The diameter of the blood vessels affects the temperature distribution during and following laser irradiation, with and without ICG. Adding 1 or 2 mg/kg bw of ICG will cause significant temperature increase (15–35°C, p ≤ 0.001) in blood vessels with a diameter of 0.1–1 mm and steep temperature gradients in 1.5–2 mm diameter blood vessels.

Conclusions: Intravenous application of ICG at 1–2 mg/kg may improve coagulation of blood vessels with 0.1–1 mm diameter irradiated with either a diode or alexandrite laser. This should be confirmed with clinical trials in the near future.

• lndocyanine green
• ICG
• laser
• leg veins
• mathematical model
• selective photothermolysis

Introduction

The well-known theory of selective photothermolysis proposed in 1983 by Anderson and Parrish is the premise for laser treatment of vascular disorders [1], [2]. At selected laser wavelengths, the laser energy absorbed by the oxy- and deoxyhaemoglobin in blood causes coagulation of blood cells and, by heat conduction, transmural coagulation of vessel walls (i.e. photocoagulation) [1], [3–6]. Laser parameters for selective photothermolysis have been determined largely through mathematical modelling. Various mathematical models have been developed to predict optimal laser parameters to achieve high-efficacy laser treatment [3], [4], [7–15]. In all of these models the skin is considered an optically turbid medium. Light propagation in a turbid medium, such as human skin, can be modelled through an analytical solution of diffusion theory and Monte Carlo simulations [14], [16]. A new approach to the diffusion approximation has been presented by Shafirstein et al. that can predict realistic temperature distributions within blood vessels in the dermis by including latent heat of evaporation, while calculating the photon flux and thermal field simultaneously via a finite element method [7]. The model was validated in animal studies and used to explain clinical outcomes of flash lamp pulsed-dye-laser (FPDL) and Nd:YAG laser treatments of vascular lesions such as leg veins and port-wine stains (PWS) [7], [17–21]. Independent research groups have been using this modelling approach to calculate temperature distribution within blood vessels [16], [22].

The practical use of this model is its ability to delineate the primary laser parameters that determine blood-vessel coagulation during laser treatments of PWS or other vascular lesions [7], [17], [18], [23]. In an in vivo model, there are hundreds of variables that must be taken into account when designing a laser study (e.g. different wavelengths, laser radiant exposures, pulse times, vessel sizes). Testing each set of variables in an animal model or clinical study is an impractical task. However, this task can be accomplished via mathematical modelling, where the various variables are tested by calculating the temperature distribution within blood vessels.

Blood coagulation within the vessel will occur at temperatures higher than 70°C [24]. The thermal damage can be restricted to the vessel and the adjacent dermal tissue is spared by using an appropriate pulse duration and wavelength [1]. Even the treatment of large vessels with diameters up to 2 mm (e.g. leg veins) is possible. Visible leg veins are present in as many as 80% of the population [25]. A variety of lasers have been used to treat such venous vessels including the FPDL at 595 nm [26], alexandrite lasers at 755 nm [27], and Nd:YAG lasers at 1064 nm [28–33]. Near infrared (NIR) light, in the range of 700–1100 nm, deeply penetrates the dermis and large vessels. Consequently, the use of NIR laser with appropriate radiant exposure and pulse duration should effectively coagulate superficial abnormal leg veins.

A review of the published studies shows that, in a clinical setting, the outcomes with NIR lasers is still suboptimal, commonly yielding incomplete clearance of leg veins [34]. It is theorised that this variability in results can be explained by the presence of vessels with different diameters within the venous lesions. Therefore, in many patients a combination of lasers is required to achieve the best possible outcomes [35]. In addition, pain during treatment is still an obstacle for laser treatment, particularly when the applied laser radiation is simultaneously absorbed in water (i.e. Nd:YAG laser, 1064 nm).

The relative low absorption coefficient of oxy-deoxyhaemoglobin to NIR wavelength enables the light to reach deeply lying vessels, but high radiant exposures are then required to induce coagulation, which brings with it the risk of unspecific tissue heating in the epidermal/dermal junction.

It was recently demonstrated that indocyanine green (ICG) and NIR diode laser induce irreversible thermal damage in vessels 0.01–0.1 mm diameter in an animal model [36]. ICG is a water-soluble tricarbocyanine dye with molecular weight of 775 (g/mol) that was first approved for clinical use by the US Food and Drug Administration in 1956 [37]. After intravenous injection, ICG binds to plasma proteins, mainly α-lipoproteins [38]. Thus, it is confined to the intravascular space, with minimal leakage from abnormal or fenestrated vessels [39]. Under physiological conditions, ICG is exclusively eliminated from the blood through the liver and excreted chemically unchanged into bile [39–42]. The half-life of ICG is approximately 10 min and there is no entero-hepatic circulation. Due to its fast pharmacokinetics, ICG allows for drug administration and light irradiation in a single session. Owing to these characteristics, ICG is clinically approved for determination of liver function, plasma volume, and cardiac output [43], [44]. The absorption spectrum of ICG dissolved in plasma exhibits a strong absorption band at about 700–810 nm [45]. After light absorption, over 85% of absorbed light energy is converted to heat inside the molecule [46].

The goal of this study is to use a validated mathematical model to examine the key variables that affect the temperature field within large blood vessels (0.1–2 mm), such as leg veins, during laser treatment with ICG. In this study the modelling was conducted for either 755 or 810 nm laser light wavelengths, which are emitted by alexandrite and diode lasers, respectively. Clinically approved laser settings and concentrations of the ICG dye were used in the simulations.

Material and methods

The laser irradiation of the leg veins was simulated using a well-developed mathematical model [7], [21]. A detailed description of the mathematical model and basic assumptions is given in Shafirstein et al. [7]. In this model, the two-dimensional (2D) time-dependent diffusion equation is derived from the equation for radiative transfer [47], [48] given by:where

is the photon fluence P_n/m²/s, where P_n is the number of photons, αⁿ is the optical diffusion coefficient (m²/s) of tissue n (epidermis, dermis, or blood) absorption, and are the linear absorption and scattering coefficients (1/m) of tissue n, g is the optical anisotropy factor, and c_n is the speed of light in tissue n.

The corresponding (2D) heat transfer equation is:where T is the temperature as a function of time (t) and space (x, z), kⁿ is the thermal conductivity of the epidermis (n = e), dermis (n = d), or blood (n = b) in W/m/°C, ρⁿ is the density of the epidermis, dermis, or blood in kg/m³, and C(T)ⁿ is the specific heat capacity of the epidermis, dermis, or blood in J/kg/°C. The blood perfusion was 0.028 kg/m³/s. The specific heat includes the latent heat L (J/kg) for evaporation of the water content at T = 100°C, as shown in Equation 3a, where it is assumed that the liquid-to-gas transition occurred over 1°C, ΔT = 1.where are the heat sources (W/m³) generated through photon absorption in the chromophores of different tissues and E_f is the volume fraction of the chromophores inside the tissue. The haematocrit (Hct) varies from 0.45 in vessels larger than 100 µm to 0.25 for 10–20-µm vessels (e.g. capillaries). In the epidermis, the volume fraction of melanosomes varies, ranging from 4% to 16% for skin types 1 to 6. In blood, it is assumed that the absorption and scattering coefficients of blood with a 0.4 haematocrit were similar to those of blood with a 0.45 Hct. In the presence of ICG, the laser absorption (μ_a laser) was calculated as a function of the Hct and the ICG volume fraction, such that:where μ_aICG is the linear absorption of plasma with ICG, μ_aHct is the linear absorption of Hct, f is the volume fraction of Hct, and (1 − f ) is considered to be the balance of ICG. For the epidermis, it is assumed that the absorption and scattering coefficients are of skin type 2 with 6% melanosomes (i.e., E_f = 0.06). The values for all the optical and thermal constants are listed in Table I

Table I.  The optical and thermal properties that were used for epidermis, dermis and blood in modeling.

Optical properties [63]	Epidermis^a	Dermis (bloodless)	Blood (0.4 haematocrit)
Laser wavelength 755 nm
μa (m^−1), absorption coefficient (blood)	1000	25	444
μa (m^−1), absorption coefficient (ICG)	–	–	1010
μs (m^−1), scattering coefficient	49 808	14 162	46 855
n, index of light refraction	1.37	1.37	1.33
g, optical anisotropy factor	0.8	0.8	0.995
Laser wavelength 810 nm^b
μa (m^−1), absorption coefficient (blood)	857	24	419
μa (m^−1), absorption coefficient (ICG)	–	–	2590
μs (m^−1), scattering coefficient	1351	1351	579
n, index of light refraction	1.37	1.37	1.33
g, optical anisotropy factor	0.8	0.8	0.995
Thermal properties [12]
k (W/m/C), thermal conductivity	0.21	0.53	0.55
ρ (kg m^−3), specific density	1200	1200	1100
Cp (J kg^−1C^−1), specific heat capacity	3600	3800	3600
L (J kg^−1), latent heat^c	1807 × 10^3	1581 × 10^3	1355 × 10^3

^aFor skin type 2 with 6 volume % melanosomes. ^bthe optical properties for 595 nm were interpolated from Table II 3.3 in Van Gemert et al. [63]. ^cthe latent heat of evaporation is for the water (2258 KJ/kg) content in blood (60%), epidermis (80%) and dermis (70%).

.

The diffusion and thermal equations (Equation 1 through Equation 3a) were solved simultaneously via the finite element method with Comsol 3.5a (Burlington, MA). Time steps as small as 10⁻¹⁶ s were used at the beginning of the laser pulse (10⁻²⁶s was considered time = 0) and were gradually increased to the microsecond range toward the end of the heating. The model geometry is shown in Figure 1.

Figure 1. (A) Schematic axisymmetric geometric model of the skin comparable to a histological slice including the epidermis (0.06 mm) as the upper layer on the top of a 3.5 mm dermis containing 13 blood vessels ranging from 0.010 mm to the maximum diameter of 2 mm of the respective test blood vessel (marked by an arrow), which is center is located at a depth of 1.5 mm below the surface of the epidermis. The symmetry axis is at the center of the laser spot or beam diameter. (B) The linear absorption of ICG (green line) is above the hemoglobin (red line) in the range of 700–850 nm. Therefore, the addition of ICG, to blood vessel, will significantly increase the intravascular absorption of laser light with either 755 or 810 nm wavelength.

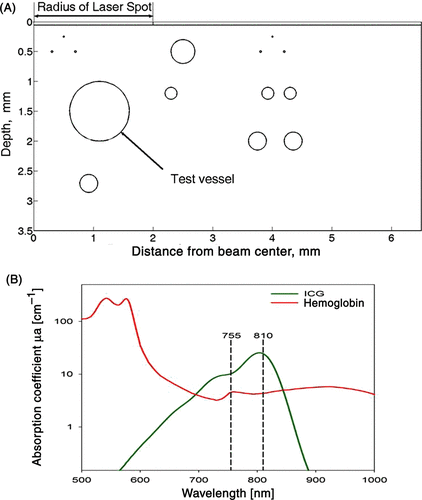
The axisymmetric geometrical model consists of an epidermis (0.06 mm thick) and a dermis containing 13 blood vessels ranging from 0.01 mm (capillaries) to the maximum diameter of 2 mm of the test vessel (marked with an arrow in Figure 1A) with a centre located at a depth of 1.5 mm below the surface of the epidermis. The symmetry axis is at x = 0 and 0 < Z < 3.5 mm. The centre of the unscattered incident laser beam (laser spot) is located at z = 0 and 0 ≤ × ≤ 2 mm (Figure 1A). This geometrical approximation for representing skin has been shown to be useful in defining optimal laser settings and predict clinical outcomes of laser thermal therapy with and without ICG [7], [17–21]. Cooling of epidermis is achieved by setting the temperature of the epidermis to 10°C. The effect of blood perfusion on the thermal field was included by assuming arterial blood temperature of 37°C. The initial and boundary conditions were similar to the ones used in previous publications [7], [21]. The lasers light wavelength was set to 755 nm or 810 nm. The optical and thermal parameters of tissue for 755 nm and 810 nm are shown in Table I. The optical properties for blood, epidermis and dermis were taken from the literature and assumed to be independent of the temperature [49], [50]. The absorption of ICG in plasma for 1 and 2 mg/kg were calculated from measurements of ICG absorption in plasma that were reported in a previous work [46]. The thermal properties were taken from our previous publication [7].

The centre of the vessels was set in the mid-dermis at a depth of 1.5 mm with diameters of 0.1, 0.2, 0.5, 1.0, 1.5, or 2.0 mm. The results are displayed in a two-dimensional vertical cut into the skin like a virtual biopsy (Figure 1A). The radiant exposure (J/cm²) and pulse duration (ms) of either laser were set to 30 J/cm² and 10 ms (3000 W/cm²), 60 J/cm² and 20 ms (3000 W/cm²), 80 J/cm² and 30 ms (2666 W/cm²), 80 J/cm² and 60 ms (1333 W/cm²) or 100 J/cm² and 100 ms (1000 W/cm²). Since high radiant exposures were applied in clinical trials [51], [52], 120 J/cm² and 60 ms (2000 W/cm²) were used for the diode laser. The ICG concentration within the blood vessels was set to either 0 mg/kg, 1 mg/kg or 2 mg/kg BW. A total of 180 simulations were conducted for a combination of six different vessel sizes irradiated with two wavelengths at five different laser settings and three different concentrations of ICG (6 × 2 × 5 × 3 = 180).

Blood flow

The effect of blood flow on the laser interaction time was included by calculating the interaction time (IntTime) between the laser light and the chromophores (ICG and blood) as a function of blood flow velocity such asyielding a value of 0.0325 s; whereas the spot size diameter of the laser was 4 mm and blood flow velocity was 123 mm/s [53]. This relatively high blood flow was used as an upper limit, since it is known that blood flow changes dramatically as function of physiological conditions and hyperthermia [54], [55]. Since light propagation in tissue is orders of magnitude higher than blood-flow speed, it was assumed that, at each time step t_i, the portion of energy that is absorbed by the blood and ICG is equal to

Thus, at each time step t_i, the number of photons (effective energy) absorbed by the exposed region is equal to the integration of laser power over time (t_i) multiplied by E_f. As the laser irradiation time progressed, the energy absorbed by the chromophores is reduced linearly. For pulse times larger than IntTime, it is assumed that this process repeats itself.

This is a first approximation to the interaction time of laser light and intravascular chromophores. In reality many factors could affect the actual interaction time. For example, light scattering may increase the effective laser beam diameter and thus increase the interaction time; however, laser heating of adjacent vessels could increase blood flow to the treated region, which will reduce the interaction time.

Mean temperature

The mean temperature within the entire vessel was calculated by retrieving the temperature from each pixel within vessel and dividing the sum of the temperatures by the number of pixels at each time step, over 0 < t < 3.5 s. These calculations were performed during the post-processing analysis.

Statistical methods

At each laser wavelength, model-predicted mean temperatures were analysed via two-way ANOVA with treatment factors being blood vessel diameter, ICG concentration, and their interaction. ANOVA post-hoc analysis consisted of pairwise comparisons of ICG concentration at each level of blood-vessel diameter. An alpha = 0.05 significance level was used despite the multiple comparisons, so as not to inflate Type II error.

Results

Figure 2 shows the calculated temperature distribution for photons having an 810 nm wavelength with radiant exposure of 60 J/cm² and 20 ms pulse time.

Figure 2. The temperature distribution in skin (two dimensional vertical cut) at the end of the pulse duration of 810-nm laser light exposure, without ICG (A–C) and with 2 mg/kg ICG (D-F). Results are shown for leg veins diameters of 0.5 mm (top), 1 mm (middle) and 2 mm (bottom) of the panel. The laser radiant exposure was 60 J/cṁ and the pulse duration was 20 ms.

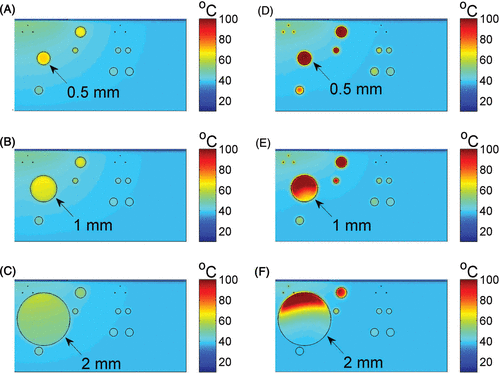
These results are for peak temperatures in the dermis, test vessel (marked with an arrow) and surrounding vessels, at the end of the laser pulse, i.e. t = 20 ms. Without ICG, the maximum temperatures at the vessels’ centres were in the range of 60–70°C (Figure 2A–C). The temperature in the epidermis was no more than 20°C, due to active epidermal cooling that was included in the simulations. Adding ICG at a dose equivalent to 2 mg/kg resulted in a significantly higher temperature (Figure 2D–F). In the 0.5 mm vessel, the temperature at within the vessel was 100°C (Figure 2D). A temperature range of 90–100°C was calculated in the upper region of the 1 mm vessel diameter (Figure 2E). In the 2 mm vessel (Figure 2F) the lower part of the vessel had temperatures in the range of 40–60°C, compared to temperatures in the range of 80–100°C in the minor upper part.

Figure 3 exemplarily shows the simulated temperature distribution when the tissue is irradiated with 755 nm light wavelength. The modelling process was identical to the one used for photons at 810 nm with the same ICG concentration, radiant exposure, and pulse duration.

Figure 3. The temperature distribution in skin (two dimensional vertical cut) at the end of the pulse duration of 755-nm laser light exposure, without ICG (A–C) and with 2 mg/kg ICG (D–F). Results are shown for leg veins diameters of 0.5 mm (top), 1 mm (middle) and 2 mm (bottom) of the panel. The laser radiant exposure was 60 J/cm² and the pulse duration was 20 ms.

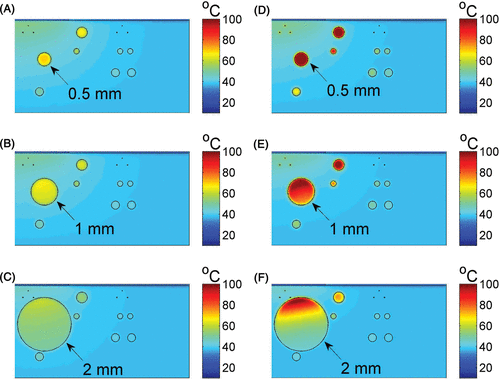
For 755 nm laser light with ICG, the heating was uniform for 0.5 mm vessel diameter (Figure 3D, 3E). The results for the 1 and 2 mm vessels resembled the diode laser (compare Figure 3F and 2F), showing higher temperatures in the upper part with lower temperatures, ranging from 40–60°C, in the lower part.

The temperatures maps calculated for all the other laser parameters with and without ICG were very similar to the ones presented in Figures 2 and 3.

Temperature profiles along the centre line of the tested blood vessels are shown in Figure 4. These high-resolution temperature curves were extracted for the 2-D data in Figures 2 and 3.

Figure 4. The temperature profile along the center line of each of the tested blood vessels from the top of the vessel (depth=0) to the bottom of the vessel. These profiles were extracted from the calculations at the end of the laser pulse (20 ms) with radiant exposure of 60 J/cm². Figures A–C are the results for 755 nm and D–F are for 810 nm, where A and D are for 0.5 mm, B and E are for 1 mm and C and F are for 2 mm vessel diameter.

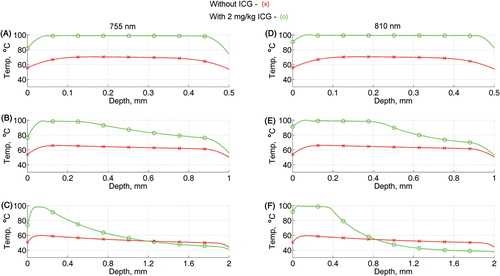
The results in Figure 4A–C are for 0.5, 1 and 2 mm blood vessels, respectively, irradiated with 755 nm light, and those for Figure 4D–F are for 0.5, 1 and 2 mm blood vessels, respectively, irradiated with 810 nm light. A laser radiant exposure of 60 J/cm² and 20 ms pulse time was used for both wavelengths. Without ICG, the temperature throughout the cross section of the vessels is below the threshold temperature, 70°C, (see red lines with × markers) for both wavelengths. Adding ICG at 2 mg/kg increases the temperature by about 35°C for vessel diameter of 0.5 mm (green line with o markers in Figure 4A and D). Consequently, with ICG, the maximum temperature in the 0.5 mm vessel is 80°C at the vessel/tissue boundaries and 100°C at the centre. For the 1-mm vessel diameter, the maximum temperature increases from 80°C to 100°C and starts to decrease, at 0.4 mm from the upper boundary, until it reaches a low level of about 50°C in the lower boundary (Figures 4B and E). A marked temperature increase and gradual decrease was calculated for the 2-mm diameter vessel, where the temperature with ICG is above the temperature without ICG within 0.8–1 mm from the upper boundary and lower than the temperature without ICG in the region of 1 mm from the lower boundary (Figures 4C and F).

The mean temperature for the different laser parameters was about the same for each specific vessel size.

The addition of ICG resulted in significant increases in the mean temperature when compared to no ICG for both wavelengths, as shown in Table II

Table II.  The temperature difference within blood vessels was calculated by subtracting the mean temperature with 0 mg/kg ICG from the mean temperature for either 1 mg/kg ICG (1-0) or 2 mg/kg ICG (2-0), and by subtracting the mean temperature with 1 mg/kg ICG from the mean temperature calculated for 2 mg/kg ICG (2-1) for each vessel size irradiated with either 755-nm or 810-nm wavelength. The mean temperature for each vessel size was calculated by averaging the temperature of all the laser settings with and without ICG.

Vessel diameter	ICG dose^a comparison	Temperature differences (P values)
		at 755 nm	at 810 nm
0.1 mm	1 minus 0	12.35 (0.0011)	31.59 (<0.0001)
	2 minus 0	23.97 (<0.0001)	43.73 (<0.0001)
	2 minus 1	11.63 (0.0020)	12.14 (0.0003)
0.2 mm	1 minus 0	22.34 (<0.0001)	37.42 (<0.0001)
	2 minus 0	34.77 (<0.0001)	39.98 (<0.0001)
	2 minus 1	12.43 (0.0010)	2.56 (0.4189)
0.5 mm	1 minus 0	24.10 (<0.0001)	31.73 (<0.0001)
	2 minus 0	29.78 (<0.0001)	33.10 (<0.0001)
	2 minus 1	5.67 (0.1216)	1.37 (0.6652)
1.0 mm	1 minus 0	15.58 (<0.0001)	24.91 (<0.0001)
	2 minus 0	22.16 (<0.0001)	24.36 (<0.0001)
	2 minus 1	6.59 (0.0731)	−0.56 (0.8606)
1.5 mm	1 minus 0	8.56 (0.0207)	12.60 (0.0002)
	2 minus 0	11.28 (0.0026)	9.01 (0.0055)
	2 minus 1	2.71 (0.4563)	−3.59 (0.2583)
2.0 mm	1 minus 0	4.85 (0.1845)	6.01 (0.0603)
	2 minus 0	5.66 (0.1223)	2.20 (0.4876)
	2 minus 1	0.81 (0.8238)	−3.81 (0.2298)

^aDoses are in units of mg/kg.

for vessels sizes in the range of 0.1–1.5 mm (temperature increases ranging from 8.6°C to 43.7°C with P values ranging from <0.0001 to 0.02). There was no significant difference in the mean temperature for 2 mm vessel irradiated with either 755 or 810 nm wavelength. These results are in agreement with the data shown in Figure 4.

Increasing the ICG concentration (from 1 to 2 mg/kg) resulted in significant temperature increases (>10°C with P values ≤0.002) for vessel sizes of 0.1 mm in diameter with both wavelengths and 0.2 mm in diameter for the 755 nm wavelength. However, for the 0.2 mm vessel size with 810-mm wavelength and vessel sizes of 0.5–2 mm diameter with both wavelengths, the increase in ICG concentration did not cause significant increases in the mean intravascular temperature (see Table II).

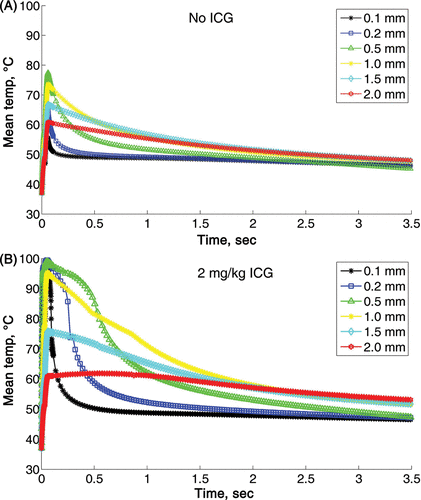
The effect of vessel size on the mean heating and cooling time is shown in Figure 5. These calculations were done for 810 nm wavelength with radiant exposure of 120 J/cm² and 60 ms pulse duration, with and without ICG. A rapid heating followed by a fast cooling was calculated for vessel sizes of 0.1–0.2 mm. The maximum temperature was for the 0.5 mm vessel. The mean temperature declined as the vessel size increased from 1 to 1.5 and 2 mm. The cooling rate was inversely proportional to the vessel size. As the vessel size increases, the cooling rate decreases (see Figure 5). Adding 2 mg/kg ICG increased the maximum temperature to 100°C for vessel size of 0.1–0.5 mm and reduced the cooling rates for all the vessels (Figure 5). For vessel size of 2 mm, the mean temperature was above 55°C for as long as 3.5 s, when the simulation ended. Similar results were obtained for all the other laser settings (data not shown).

Figure 5. The course of mean temperature in different vessels is shown during 3.5 seconds after 810-nm diode laser exposure without (A) and with 2 mg/kg ICG (B). The laser parameters in both cases were radiant exposure of 120 J/cm² and 60 ms pulse time.

Discussion

Laser-induced thermal coagulation of abnormal blood vessels requires an optimal setting of parameters such as wavelength, pulse duration and radiant exposure. The wavelength must be carefully selected to allow for sufficient penetration to reach the target vessels in the dermis and a critical temperature of 70°C should be exceeded during treatment.

NIR laser light penetrates deeper into the skin, but the absorption of NIR light radiation in haemoglobin is relatively low (420–440 m⁻¹, see Table I and Figure 1B). This frequently causes insufficient coagulation of small vessels and leads to suboptimal clinical outcomes [21]. As long as laser therapy is based on light absorption in haemoglobin, this problem persists. This limitation can be overcome by introducing an exogenous chromophore, such as ICG, that augments light absorption in the presence of haemoglobin. The high absorption of NIR light by ICG, 2590 m⁻¹ (810 nm) and 1010 m⁻¹ (755 nm) (Table I and Figure 1B), will increase intravascular temperatures, but could also decrease light penetration within large blood vessels. The mathematical analysis in this paper suggests that the addition of ICG could significantly enhance thermal coagulation of vessel sizes in the range of 0.1–1 mm in diameter. In a clinical scenario, this would result in complete thermal damage, and highlights the relevance of laser-ICG interaction as a potential therapeutic tool. The mathematical analysis also suggests that the addition of ICG will cause partial coagulation in 1.5 and 2 mm vessels. Obviously, due to the increase of absorption in the presence of ICG, most of the incoming photons are absorbed in the upper part of the vessel and only a minor part reaches the bottom of the vessel. This is consistent with published data where partial coagulation of large blood vessels was observed in histological sections taken from skin of vascular lesions irradiated with FPDL that has high absorption in blood [56]. Laser-induced thermal injury to the upper part of these large blood vessels could cause platelet aggregation and eventually lead to thrombotic vessel occlusion. Therefore, it can be assumed that ICG-enhanced NIR laser irradiation can be used to clear blood vessels up to 1 and maybe even 2 mm in diameter. This prediction needs to be verified in clinical trials.

The thermal maps with and without ICG indicate that the temperature at the epidermis will not exceed 30–40°C, so no significant skin damage is expected in this setting. The calculated temperature in the dermis (40–60°C) with ICG suggests that minimal pain and adverse events may occur. Dermal heating is a major concern in the treatment of leg veins with NIR lasers [21]. Pain can be minimised by using small beam size (e.g. 4 mm) and minimal radiant exposure in addition to skin cooling [21]. This recommendation should be also valid for ICG-enhanced NIR laser therapy.

The mathematical analysis in this study suggests that vessel size is the critical factor affecting the response to laser therapy with and without ICG, for a range of laser settings that are used in the clinic. This result is in agreement with previous studies, which demonstrated that the size of blood vessels is the most important variable that affects the intravascular temperature during selective photothermolysis [7], [20], [22], [57]. In clinical practice, it is almost impracticable to determine the size of the target vessels during or before therapy. This obstacle can be addressed by using FPDL with high blood absorption to treat vessels in the range of 0.05–0.5 mm and NIR lasers to treat larger vessels such as 0.5–1 mm [17], [21].

Herein, we postulate that a wide range of vessel sizes can be targeted with a single laser wavelength of either 755 nm or 810 nm by adding ICG to the blood vessel prior to laser irradiation. This hypothesis is supported by the mathematical analysis in this paper for vessel sizes of 0.1–2 mm, and previous work where it was demonstrated, via mathematical modelling validated with an animal study, that 810 nm laser irradiation preceded by ICG administration significantly enhances the coagulation of 0.01–0.1 mm blood vessels [20].

To date, only a few clinical trials were performed with diode lasers in leg veins using different laser parameters [58]. Radiant exposures ranged from 150 J/cm² (50 ms) to 346 J/cm² (600 ms) at 4 mm spot size to achieve vessel coagulation [51]. Others used multiple stacked pulses with 210–336 J/cm² (50 ms) at a 3-mm spot size [52]. These high radiant exposures and pulse times will cause significant heating of the dermis and epidermis that will increase pain and the risk of skin damage [21]. Lowering the radiant exposure will reduce the side effects but also the temperature within the vessels below the 70°C threshold, as the results in this study suggested. However, the threshold temperature can be exceeded by using relatively medium levels of radiant exposures (60–100 J/cm²) with 1 or 2 mg/kg of ICG (data in Table II).

In blood vessels with larger diameters (1.5, 2 mm), the mean temperature is below the threshold temperature, even with ICG, which is mainly caused by the steep temperature gradient within these vessels, as seen in Figure 4. This gradient resulted from the high absorption of the NIR light by the ICG component within the vessel. Nonetheless, the upper part of the vessel wall will be exposed to temperature above 70°C (Figure 4C, 4F), which could result in vessel occlusion, as discussed above.

Our analyses also suggest that doubling the ICG concentration (from 1 to 2 mg/kg) results in only a slight increase of the mean temperature for vessel size of 0.2 and 0.5 mm and a decrease in the mean temperature for vessels size of 1–2 mm (Table II). Hence, it is sufficient to have 1 mg/kg of ICG in blood vessels to significantly increase the temperature above the 70°C threshold, and in both concentrations the mean temperatures will be comparable (Table II). These results have potential therapeutic implications. Because the half-life of ICG is 10 min in plasma, by using laser parameters which result in the same mean temperature for 2 and 1 mg/kg of ICG, the actual therapeutic window is 50% longer; i.e. 15 min, which is sufficient time to treat leg veins or vascular lesions with a NIR laser.

The effect of vessel size on the heating and cooling times was demonstrated by plotting the temperature as a function of time for representative laser settings and ICG concentrations (Figure 5). The cooling of a heated vessel is mainly caused by heat conduction through the vessel wall into the dermis. In this mechanism of heat transfer, the cooling rate is a function of the surface-to-volume ratio, which decreases with vessel size. Therefore, smaller vessels will cool faster than larger ones. An increase in vessel diameter slows the cooling rate and significantly prolongs the cooling time, which would increase the delivered thermal dose and may lead to thermal coagulation of large vessels.

Conclusion

The treatment of leg veins with lasers is still a challenging procedure. The use of NIR lasers such as alexandrite (755 nm), diode (800 nm) or Nd:YAG (1064 nm) lasers precludes efficient coagulation of a wide range of blood vessels.

Our modelling work suggests that adding a clinically approved dose of 2 mg/kg of ICG dye may improve clinical outcomes for lesions with vessel sizes in the range of 0.1–1.0 mm. Our simulations indicate that there is a wide range of laser settings suitable for the treatment of these lesions in conjunction with ICG administration. Importantly, a similar benefit was found for either 1 or 2 mg/kg of ICG, which would clinically translate into a 50% increase of the therapeutic window. The modelling allows us to delineate clinically valid laser parameters and ICG concentrations that can be used to design clinical trials to test the validity of these results. Despite the clear results of our modelling, it should be emphasised that clinically effective vessel coagulation cannot be accurately calculated. Even successful photocoagulation of vessels by means of laser irradiation could be clinically ineffective due to vessel repair. However, when comparing the results with and without ICG, there is a clear benefit of using ICG in addition to haemoglobin.

Declaration of interest: The study was supported in part by funding from ZIM, Germany (grant number KF2525601FR9). This study was also supported in part by the University of Arkansas for Medical Sciences College of Medicine Children's University Medical Group Fund Grant Program, and by NSF and Arkansas Science and Technology Authority grant number G1–35321–01. All authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.