Temperature distribution analysis of tissue water vaporization during microwave ablation: Experiments and simulations

Abstract

The temperature distribution in the region near a microwave antenna is a critical factor that affects the entire temperature field during microwave ablation of tissue. It is challenging to predict this distribution precisely, because the temperature in the near-antenna region varies greatly. The effects of water vaporisation and subsequent tissue carbonisation in an ex vivo porcine liver were therefore studied experimentally and in simulations. The enthalpy and high-temperature specific absorption rate (SAR) of liver tissues were calculated and incorporated into the simulation process. The accuracy of predictions for near-field temperatures in our simulations has reached the level where the average maximum error is less than 5°C. In addition, a modified thermal model that accounts for water vaporisation and the change in the SAR distribution pattern is proposed and validated with experiment. The results from this study may be useful in the clinical practice of microwave ablation and can be applied to predict the temperature field in surgical planning.

• Enthalpy
• microwave ablation
• SAR
• temperature field
• water vaporisation

Introduction

Hepatocellular carcinoma (HCC) is widely considered to be one of the most deadliest diseases, with a mortality rate of 100% at 5 years after diagnosis in untreated cases, resulting in the death of more than one million people each year worldwide [1], [2]. In China, HCC is the second most common malignancy [3]. Although surgical resection is the only potentially curative approach for patients with HCC, most patients are not candidates for the procedure due to anatomical limitations, an inadequate functional liver reserve, or extra-hepatic metastatic lesions [4]. However, image-guided focal thermal ablation using a variety of energy sources continues to gain favour as a promising alternative treatment for tumours [5], [6].

Microwave (MW) ablation has recently been promoted as a minimally invasive technique and is widely used as an effective approach to treat HCC [7–13]. MW ablation has several advantages over radio-frequency (RF) ablation: it produces a higher ablation temperature, allows for larger tumour ablation volumes, a faster ablation time, and is better able to perform multiple ablations simultaneously [14], [15]. It is essential to know the temperature distribution during these thermal therapies, because temperature is an objective criterion by which to evaluate coagulated necrosis. Most studies indicate that complete necrosis can occur at 54°C for 1 min, or instantaneously when the tissue temperature exceeds 60°C [16–19]. To calculate the complete time-dependent temperature field that is induced by an implanted MW antenna, a wide variety of simulation methods have been proposed [20–24]. Recently, many theoretical models predicting thermal profiles and subsequent tissue damage have played a substantial role in the understanding and development of devices used for thermal ablation [25–27].

Unfortunately, the temperature simulations have not yet achieved the precision that is required for clinical application (prediction error ≤5°C). This is due to several factors such as individual variability, varying thermo-physical properties, and complicated bio-heat transfer mechanisms that are difficult to model. Current theory can predict the temperature in a region far from the antenna almost exactly [20], but the physical factors (defined in numeric simulations) that affect the temperature transition in the near-antenna region during MW ablation are extremely complex, leading to results where the temperature differences between simulations and measurements can vary greatly. This is likely attributable to water vaporisation in tissues when the temperature in the near-antenna region exceeds 80°C [28].

In this paper we attempt to improve the accuracy of temperature predictions for the near-antenna region by incorporating simple water evaporation-related processes into our simulations. These processes include water vaporisation in tissue and subsequent tissue charring, and we believe these may be the dominant heat transfer processes when tissue temperature reaches approximately between 80°C and 100°C. Without considering these processes at such elevated temperatures, results from simulations involving the bio-heat equation may differ significantly from experiments.

The most critical parameter affecting the temperature distribution is the SAR, which describes the heating ability of a heat generator that uses thermal ablation. Above 100°C, a large amount of the heat will be accumulated around the MW antenna and produce tissue carbonisation, which substantially changes the tissue's thermal properties [19], [29], [30]. The SAR distribution is affected by the change in the electrical conductivity as a function of temperature, so that the SAR pattern results in changes in the rate of temperature increase. In light of the above, we calculated the high-temperature SAR (for temperatures ≤100°C) using temperature measurements in an ex vivo porcine liver during heating and cooling phases. The low-temperature SAR (for temperatures <100°C) was determined from the initial temperature transient as measured at various locations.

The finite element software ANSYS (version 9.0, Canonsburg, PA, USA) was employed to simulate the temperature field, which attributed vaporisation phenomena to phase changes. The latent heat absorption was calculated in the simulations using an enthalpy-based method for water vaporisation. The two SAR distributions described above and the enthalpy of the liver tissue were then used in the Pennes equation to determine the temperature field. The effects of water vaporisation and tissue charring with rising temperature were also investigated. The temperature curves produced by the finite-element model (FEM) were then compared to the experimentally measured temperatures. Finally, a modified thermal model is applicable at temperatures where water evaporation is sure to occur, by adding one additional item and modifying another on the basis of the Pennes equation.

Materials and methods

Experimental system

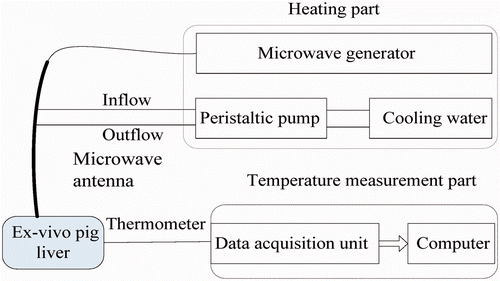
A microwave generator designed by the Institute of Microwave Electronics, Nanjing Qinghai, China, was used in the present MW ablation study. It operated at 2450 ± 50 MHz with a power output of 0–100 W. The heating system was equipped with a low-loss cable (0.10 dB/m), a water-cooled MW stub antenna (1.9 mm in diameter and 150 mm in length) with a Teflon surface coating to prevent tissue adhesion, and a BTDI-100 peristaltic pump (Baoding Longer Precision Pump, Hebei Province, China) to adjust the rate of cooling water flow within the antenna (Figure 1).

Figure 1. The heating system, including (a) peristaltic pump, (b) MW generator, (c) water-cooled antenna, (d) MW radiator.

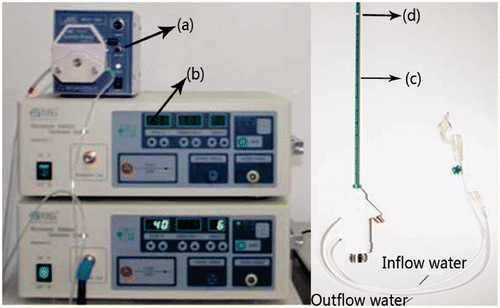
The temperature in the porcine liver was measured using iron-constantan thermocouples (TCs) because of their fast rise time, good sensitivity, and low susceptibility to microwave pickup [29], [31]. The TCs were 0.075  mm in diameter (Omega Engineering, Stamford, CT, USA). Data acquisition was performed using a 32-channel digitiser (HP34970A, Agilent, Santa Clara, CA). A schematic of the experimental system is shown in Figure 2.

Figure 2. Schematic of the experimental systems.

Ex vivo porcine liver and its properties

Ex vivo experiments on porcine liver were performed to validate the results from our computer simulations. Porcine livers of greater than 8 cm in thickness were obtained from a local slaughter house and were kept refrigerated overnight. For our calculations, we used thermal properties as described in the literature [20], which are shown in Table I.

Table I.  Thermal properties of ex vivo porcine livers.

Temperature	20–70°C	80–100°C	110–120°C
K (W/m°C)	0.465	0.867	1.460
C (J/g°C)	3.628	3.858	3.986
ρ (kg/m^3)	1020

Numeric simulation

Thermal diffusion and conduction in biological tissue may be described by the Pennes bio-heat equation as follows [32]:where T is the temperature, ρ is the tissue density (kg/m³), c denotes the specific heat (J/kg°C), K is the thermal conductivity (W/m°C), W_b is the blood perfusion (kg/m³s), C_b is the specific heat of blood (J/kg°C), T_b is the temperature of arterial blood (°C), Q_r (W/m³) is the heat generated by MW heating, and Q_m (W/m³) is the heat generated by the metabolism of the organism.

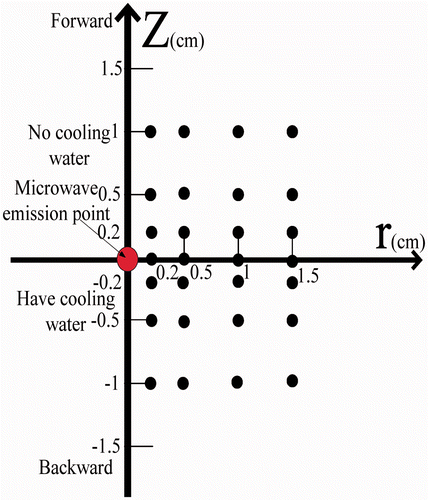
The temperature distribution during the heating process was calculated using a numerical model of the Pennes bio-heat equation, which was solved by the commercially available software package ANSYS using 2-D FEM models. The domain consisted of 4.5 cm in the r direction and 10 cm in the z direction. The near-antenna region was defined as (0 < r < 1 cm, −1 < z < 1 cm), everywhere else was considered as the far-antenna region. Figure 3 shows the model geometry, reflecting the experimental set-up. The mesh areas defined by (0,  0) to (0.09,  1.5) and from (0,  0) to (0.09,  −5) represented forward and backward antenna parts, respectively, with all other regions modelled as containing porcine liver tissue. The thermo-physical parameters for the antenna are shown in Table II. We used a mesh resolution of 0.03 cm × 0.1 cm and 0.09 cm × 0.1 cm for the antennal region and for the tissue region, respectively. The initial and boundary conditions were set to 20°C, and the size of a simulation time was set to 1 s.

Figure 3. FEM model (units in cm).

Table II.  Thermal-physical parameters of MW antenna.

	Forward	Backward
K (W/m°C)	0.6	0.6
C (J/g°C)	0.5	3.5
ρ (kg/m^3)	6.5	3.5

SAR distribution

To model the thermal distribution in the liver, the SAR distribution must be determined. This can be accomplished in theory by solving Maxwell's equations, but in practice such a calculation is highly dependent on a number of factors, such as the shape of the volume containing the reference mass, the spatial discrete step size, the particular treatment of internal air bubbles, etc. Different choices for such factors can produce significant discrepancies in the results [33]. In addition, complex reflection and refraction of electromagnetic waves arise during the thermal therapy, considering that the MW energy is mainly deposited in the near-antenna region of the tissue. Therefore, we found it impossible to calculate the SAR quantitatively.

Empirical methods to obtain SAR distributions are widely employed in hyperthermia therapy [34], [20], [29]. We performed SAR measurements in the ex vivo porcine liver, where we determined the low-temperature SAR from the initial temperature transient, while the high-temperature SAR was inferred from the rate of change of the temperature differences between experiments during the cooling phase and the heating phase.

Experimental methods

Ex vivo porcine liver heating experiments were performed to validate the computer simulation results. The data acquisition module was connected to a computer through an RS-232 interface to monitor dynamic temperature change, with a sampling frequency of 1  Hz. The flow velocity of the cooling water in the antenna was adjusted to 0.1 m/s, to reduce the carbonisation of tissue near the microwave antenna by reducing the very high ablative temperature there.

The initial liver tissue temperature was approximately 20°C. We selected the most uniform tissue containing the fewest blood vessels for the experiments. The microwave heating power in all experiments was 60 W. Because of the expected axisymmetrical distribution of the temperature around the MW antenna, the antenna and TCs were positioned in a plane and secured in place with a specially designed device as shown in Figure 4. The transient temperatures of the TCs were measured from the instant that MW power was switched on.

Figure 4. Geometry of antenna and TCs placed in the ex vivo porcine liver.

A cylindrical coordinate system (r,  z,  θ) was adopted for the experiments with the z axis running along the antenna, and the angular coordinate θ being ignorable from symmetry. The four reference points of (r,  z) = (0.2,  0), (0.5,  0), (1,  0), and (1.5,  0) were chosen to compare temperature profiles between simulation and experiment. As shown in Figure 4, 16 TCs were placed in the region z ≥ 0 and 12 TCs were located in the region z < 0. Temperature measurements from these 28 TCs were obtained in repeated experiments and then averaged to yield the final temperature results.

Results

Low-temperature SAR measurement

Since the ex vivo porcine liver lacked blood perfusion and metabolism, W_b and Q_m were taken as zero. At the instant power was switched on, the conduction heat transfer was negligible ( ≈ 0). Under these conditions Equation 1 can be simplified, and the SAR is simply proportional to the partial derivative of temperature with respect to the heating time:

In determining the SAR, the literature [35] suggests that thermal diffusion effects are negligible if the duration of the applied power pulse is restricted to ≤10 s, so only the direct MW energy deposition in the tissue affects the temperature distribution during 0–10 s. The transient temperature rise versus time was determined at each TC within the first 10 s, and a linear least-square residual fit was performed on the curve. The slopes of the lines give dT/dt at the location of the corresponding TC and are shown in Table III.

Table III.  dT/dt data at each TC.

z (cm)	r (cm)
	0.2	0.5	1	1.5
1	1.587	0.636	0.056	0.021
0.5	4.218	1.365	0.143	0.076
0.2	4.542	1.660	0.166	0.094
0	4.652	1.743	0.112	0.076
−0.2	4.135	1.621	0.144	0.085
−0.5	3.676	1.308	0.111	0.058
−1	2.415	1.122	0.073	0.032

We verified axial symmetry of the SAR distribution in the homogeneous liver tissue [20], [29], and checked that the variation in the θ direction was negligible. Next, it was convenient to fit an analytical expression to the SAR data. SAR resembled a second-order polynomial in the forward z-direction (for z ≥ 0), and gave a good fit for an exponential decay in the r-direction. For z < 0, the analysis software TableCurve 3D (version 4.0, Systat Software, Evanston, IL, USA) was used to fit the dT/dt data, where we selected an equation for its simplicity and good convergence. The forward and backward SAR distributions are well approximated by the following:

Measurement of the temperature distribution

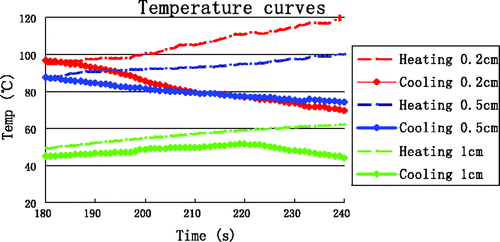
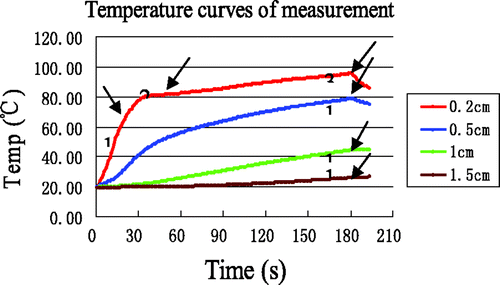
18 MW ablation experiments were performed with the ex vivo porcine liver with a heating time of 3 min. The average temperature measurements at the four reference points are shown in Figure 5, where it can be seen that the rate of temperature changes near the antenna ((r, z) = (0.2, 0), (0.5, 0)) was much greater than in the far field region, due to the localisation of MW heating. In contrast, the temperature curves in the region far from the antenna were much smoother, since a rise in temperature there is mainly the result of thermal conduction. Interestingly, the initial temperature rise at (r, z) = (0.2,  0) was rapid, with the temperature reaching ∼80°C after about 35 s, after which the temperature nearly plateaus, increasing at a slower rate from 80°C to 100°C. In addition, the temperatures at (0.2, 0) and (0.5, 0) began to decline after 180s (as the MW power was switched off), whereas the temperatures at (1, 0) and (1.5, 0) continued to ascend after 180 s due to thermal conduction. According to the literature [28], Figure 5 can be divided into three distinct time intervals, labelled 1, 2, and 3. Interval 1 of the temperature curve is slightly concave, starting from the initial tissue temperature and ending somewhere between 65°C and 70°C. Interval 2 is convex and appears as a transition between intervals 1 and 3. In interval 3, the rate of temperature increase is very slow.

Figure 5. Measured temperature curves at the four reference points. The arrows identify the end of each time interval.

The errors for the experimental measurements, defined by the difference between measurements and the average of the measurements, are calculated via Equations 5, 6 and 7, which yield the maximum error (α), minimum error (β) and the average error (γ), respectively.where i and represented time and initial time of one region; j and m denote sequence number and the total number of control curves, respectively. Table IV lists these errors for the four reference points in the experiments.

Table IV.  The errors for temperature measurement data.

	(0.2, 0, 0) Regions			(0.5, 0, 0) Regions	(1, 0, 0) Regions	(1.5, 0, 0) Regions
Errors	1	2	3	1	1	1
α (°C)	7.82	8.07	4.66	7.55	5.68	3.96
β (°C)	0.12	1.26	0.15	0.89	0.16	0.14
γ (°C)	3.43	5.32	1.28	2.68	1.91	0.97

Simulation of temperature distribution using low-temperature SAR

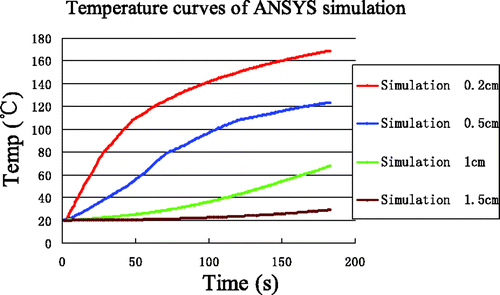
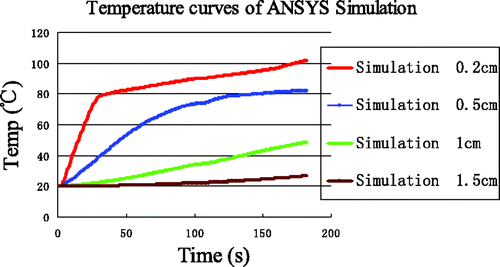
Using the low-temperature SAR data, the results of simulations for the four reference points are shown in Figure 6. The temperature rise at (0.2,  0) was rapid and reached 100°C within 40 s. Furthermore, a maximum temperature of 170°C was reached within 3 min. The greatest differences between experiment and simulation (Figures 5 and 6) are for the point nearest to the antenna (0.2, 0), where the experimentally observed inflexion point (at approximately 80°C) never appeared in the simulation curve.

Figure 6. Simulation temperatures at the four reference points.

To quantify the differences between simulation and experiment, Figures 5 and 6 are overlaid in Figure 7. The errors between simulation and measurement are produced in Table V. The most significant deviations were seen in the time interval 3 near the antenna (0.2, 0) where the maximum error, minimum error and average error was 73.23°C, 38.90°C and 50.67°C, respectively.

Figure 7. Comparison between simulation and experiment. Curves without markers are experimental measurements. Curves with markers are from computer simulation. The arrows identify the end of each time interval.

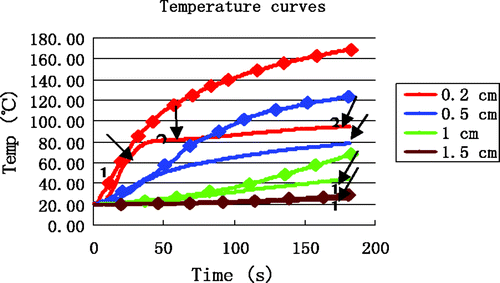
Table V.  The errors between simulation and measurement.

	(0.2, 0) Time interval			(0.5, 0) Interval	(1, 0) Interval	(1.5, 0) Interval
Errors	1	2	3	1	1	1
α (°C)	7.32	21.89	73.23	45.28	22.90	3.04
β (°C)	1.43	9.41	38.90	0.99	0.56	0.00
γ (°C)	4.87	14.67	50.67	20.48	8.79	1.15

Simulation of temperature distribution with inclusion of enthalpy

ANSYS treats the coagulation and vaporisation phenomena in the heat transfer process as a phase change problem. A phase change problem is actually a non-linear transient thermal analysis problem, in which the latent heat absorbed and released is taken into account. The effect of latent heat absorption during a phase change was incorporated in the simulation via an enthalpy method, where the enthalpy as a function of temperature can be written as [36]:Here ρ is the density in kg/m³, and c is the specific heat in J/kg°C. The unit for enthalpy is J/m³ in the literature referenced [37], [38].

Because water vaporisation activity is largely unpredictable due for heterogeneous tissue, it was very difficult to specify the temperature range of the plateau period. For simplicity, the temperatures ranging from 80°C to 100°C were considered as the main stage of vaporisation, with the increase in enthalpy in the range from 20°C to 80°C and from 100°C to 200°C being the energy needed for a temperature increase. So for example the enthalpy at 100°C was assumed to be the sum of the enthalpy value at 80°C, the energy required for the temperature increase from 80°C to 100°C and the energy required for water vaporisation. Explicitly, we writeWe hypothesised that the water content of the ex vivo porcine liver was about 70%, and the enthalpy was calculated by assuming evaporation of 90% of the water at 100°C. The results are shown in Table VI.

Table VI  Enthalpy values of ex vivo porcine liver.

Temperature (°C)	20	80	100	120	200
Enthalpy (J/m^3)	0	2.38E8	1.518E9	1.606E9	1.956E9

Figure 8 shows the simulation temperature curves when enthalpy is incorporated. The temperature curve at (0.2, 0) exhibited a significant inflection point at about 80°C and all temperature values decreased when compared with the no-enthalpy results.

Figure 8. Temperature simulation at the four reference points after incorporating enthalpy.

To illustrate how the inclusion of enthalpy improves the simulation results, the simulation results are shown together with the experimental data in Figure 9. Compared with Figure 7, simulation curves in Figure 9 clearly lie much closer to the experimental curves, particularly near the antenna at (0.2, 0). Simulation temperatures are still somewhat higher than the measured temperatures, but it must be considered that the simulation did not incorporate all water-related processes affecting the final tissue temperatures. These unaccounted for processes included tissue water evaporation, diffusion, water vapour diffusion, and condensation. A full simulation that includes models of all water-related processes would be extremely complex and is beyond the scope of our paper. The errors between simulations that included enthalpy considerations and experimental results are shown in Table VII.

Figure 9. Comparison between simulation with enthalpy considerations and experiment. Curves without markers are measurements. Curves with markers are results from computer simulation. The arrows identify the end of each time interval.

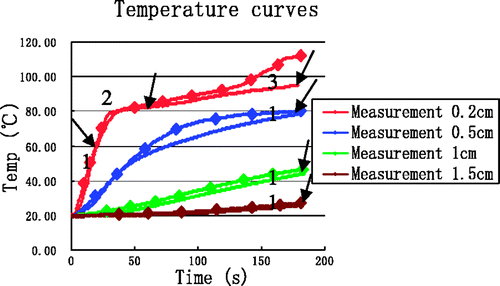
Table VII.  The errors between simulation incorporating enthalpy and experimental data.

	(0.2, 0) Time interval			(0.5, 0) Interval	(1, 0) Interval	(1.5, 0) Interval
Errors	1	2	3	1	1	1
α (°C)	5.29	7.57	18.10	7.45	3.61	3.27
β (°C)	0.92	1.45	1.98	0.91	0.59	0.00
γ (°C)	3.46	3.78	11.45	5.63	1.81	1.11

High-temperature SAR measurement

The SAR distribution when the tissue temperature is over 100°C is very different, due to tissue charring. In addition, over a longer heating period, the heat transfer from conduction becomes non-zero . Therefore, the high-temperature SAR equation could not be inferred in the same manner as in the low-temperature SAR scenario. In contrast to the Pennes equation for the non-heating state, a thermal load term was added for the heating state. Thus, we assumed that the high-temperature SAR was proportional to the partial time derivative of the temperature difference between the two states, i.e.:where ρ and c were kept the same for the two different states.

We designed experiments to empirically determine the SAR wherein two groups of tests were performed, with one being the heating group and the other the cooling group. The heating duration in the heating group tests was 4 min. The cooling group's heating was stopped after 3 min, but the data acquisition process would continue for an additional 1 min. The experiments were repeated 12 times each for the heating group and the cooling group. Figure 10 shows the average temperatures in minute 4 for the heating and cooling groups as measured at the four reference points.

Figure 10. Average temperatures in the fourth minute of heating and cooling experiments.

After the temperature difference between the heating and cooling states at each TC was determined, the following analytical expressions worked well to describe the temperature differences, as it effectively filtered out conduction effects and yielded linear and reproducible results [39].where we took  = 60 s.

In tissue regions far from the antenna the temperature was mainly the result of thermal conduction, and those regions are not subject to tissue carbonisation as in the case for tissue close to the antenna. Therefore, the far-field regions were not subject to the high-temperature SAR. The data from TCs near the antenna is shown in Table VIII.

Table VIII.  data from TCs near the MW antenna.

z (cm)	r (cm)
	0.2	0.5	1
1	0.251	0.082	0.029
0.5	1.286	0.394	0.114
0.2	1.588	0.621	0.227
0	1.703	0.845	0.329
−0.2	1.563	0.597	0.206
−0.5	1.378	0.433	0.121
−1	0.912	0.269	0.043

Both the forward and backward high-temperature SAR were modelled using an exponential fit in the r-direction and quadratic polynomial fits for the z-direction. The analytic expressions are as follows:

Simulation of temperature distribution with inclusion of high-temperature SAR

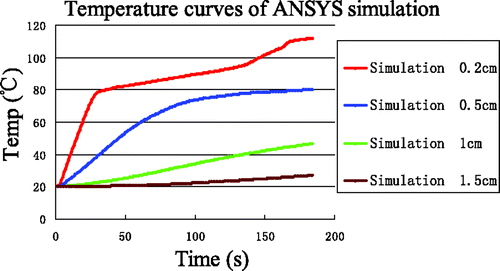
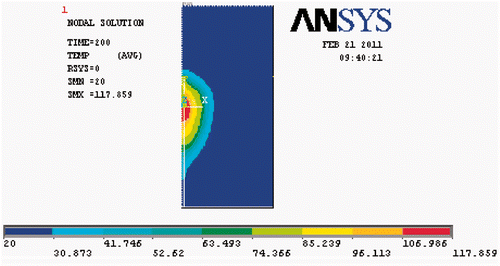
High-temperature SAR was loaded into ANSYS to simulate elevated temperature field (T ≥ 100°C). Because tissue carbonisation is negligible for the temperature distribution far from the antenna, the high-temperature SAR was only loaded in the near-antenna region, i.e. the range 0 < r < 1 cm and −1.0 < z < 1.0 cm. The temperature field and temperature evolution at the four reference points produced by the simulation are shown in Figures 11 and 12, respectively.

Figure 11. Simulation results of temperature field at t = 180 s.

Figure 12. Temperature evolution from simulations incorporating enthalpy and high-temperature SAR.

Compared with Figure 8, the temperature increase above 80°C at (0.2, 0) in Figure 12 is seen to be markedly slowed. In contrast, the temperature increase at (0.5, 0) and (1, 0) is slightly accelerated. The temperature increase at the point (1.5, 0) did not change, unsurprisingly. The improvement in simulation results when the high-temperature SAR is included, we plot these results together with experimental data in Figure 13. Clearly, the simulation temperatures are in good agreement with the measurements at the four reference points. The errors between this simulation and the measurements have significantly decreased at (0.2, 0) and are presented in Table IX.

Figure 13. Comparison between simulation incorporating enthalpy and high-temperature SAR with experimental data. Curves without markers are measurements. Curves with markers are from computer simulation. The arrows identify the end of each time interval.

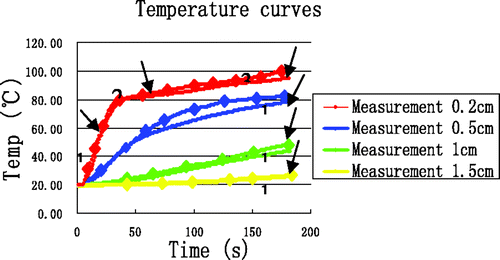
Table IX.  The errors between simulations including enthalpy and high-temperature SAR and measurements.

Errors	(0.2, 0) Time interval			(0.5, 0) Interval	(1, 0) Interval	(1.5, 0) Interval
	1	2	3	1	1	1
α (°C)	2.96	3.43	5.62	5.91	3.21	2.22
β (°C)	0.24	0.87	0.26	0.89	0.42	0.00
γ (°C)	1.28	1.34	2.16	2.24	1.45	1.04

Simulation accuracy and validation

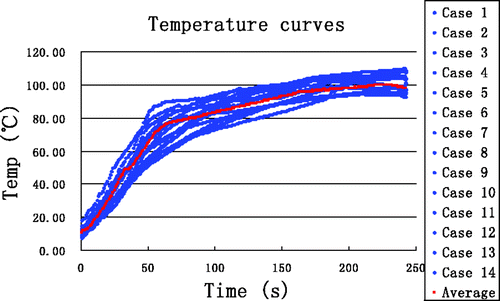
In order to validate the accuracy of the proposed thermal model in the simulations, 14 experiments with a heating time of 4 min were performed. To ensure minimal effects due to TCs on the overall thermal conductivity, only two TCs were inserted at (0.5, 0) and (1.0, 0), somewhat near the antenna. The results of all measurements at the point (0.5, 0) from all experiments are shown in Figure 14, where the red curve represents the average. The temperature curves from simulation and experiment are in good agreement for the two locations at (0.5, 0) and (1.0, 0) (Figure 15). Table X reveals that the maximum error and the maximum average error between simulation and measurement are 6.75°C and 3.97°C, respectively, and that all average errors are less than 5°C.

Figure 14. Measured temperature from 14 experiments and at (0.5, 0); red curve is average.

Figure 15. Comparison between simulation based on the proposed thermal model and experiment. Curves without markers are experimental results. Curves with markers are from computer simulation. The arrows identify the end of each time interval.

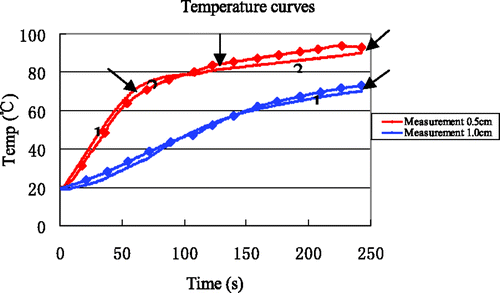
Table X.  The errors between simulation and measurements.

	(0.5, 0, 0) Time interval			(1, 0, 0) Interval
Errors	1	2	3	1
α(°C)	5.84	3.86	6.75	4.68
β (°C)	1.05	0.82	0.22	0
γ (°C)	3.28	1.11	3.97	2.09

Discussion

It is well known that the heat of vaporisation and the specific heat of water are 2260 kJ/kg°C and 4.2 kJ/kg°C, respectively. This means that the heat required for vaporisation of water at 100°C is about five times the heat that is required to raise the temperature of an identical amount of water from 0°C to 100°C. Thus, as energy is used to convert liquid water to vapour, less energy is available to increase the temperature during porcine liver MW ablation. We can infer that the change in the rate of temperature increase at the beginning of the plateau period in our data is due to water vaporisation (see Figure 7). That vaporisation takes place in significant quantity during the experiments is not in doubt, since the sizzling sounds consistent with boiling water in organ tissue can be heard during the heating process, and vapour can also be seen to rise from the tissue surface in the process.

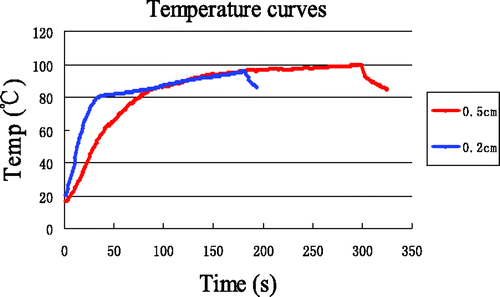
Because the plateau period in Figure 5 was only visible for data from the point (0.2, 0), ten additional experiments were performed with a heating time of 5 min, to further investigate the plateau period. Temperatures were measured at a different point (0.5, 0), and the average temperature curve is shown in Figure 16, together with the data from Figure 5. We can see that the plateau period for the new point also appears when the temperature is between 80°C and 100°C. Therefore, the plateau period is in general encountered for times when the tissue temperature is between 80°C to 100°C. Compared with the plateau period for the point at (0.2, 0), the slope of the curves and the curvature of the inflexion point in the plateau period for the point (0.5, 0) are smaller.

Figure 16. Temperature at (0.5, 0) with 5 min heating compared with that at (0.2, 0) with 3 min heating.

When the temperature exceeds 100°C, Figure 9 illustrates that the simulated temperature curve at (0.2, 0) undergoes a drastic transition, which is characterised by an accelerated rate of increasing temperature. However, the same phenomenon is not observed in the experimental data. The difference between simulation and measurement above 100°C is likely the result of tissue charring. A carbonisation strip near the MW antenna can be observed after the experiments, and carbonisation will reduce the local heat conductivity and ablation lesion [29]. Furthermore, impedance mismatches between the antenna and the surrounding tissue become evident at high-temperatures. A high proportion of energy will be reflected, heating the antenna, which may reduce energy absorbed by the tissue [10], [40]. After incorporating the high-temperature SAR, which is closely related to tissue carbonisation, into the simulation, the simulation accuracy is significantly improved (Figure 13).

The Pennes equation is a remarkably effective method for modelling heat transfer in tissue during thermal ablation. However, it does not account for energy loss due to water vaporisation and subsequent tissue carbonisation at the elevated temperatures. We have attempted to improve the thermal model by incorporating some simple water evaporation-related processes. Considering the fact that a wide variety of biological tissues have a high water content, during evaporation the water content can drop dramatically and copious latent heat will be absorbed in the process. To account for the energy expended to vaporise water, a new item, namely the enthalpy H(T), was added to yield a modified bio-heat equation. In addition, when the tissue temperature exceeds 100°C, tissue charring results in a reduction of the energy that is absorbed in tissue close to the antenna, which alters the radiation pattern [21]. To map the tissue carbonisation to the change of the SAR pattern, the item Q_r was modified. With these modifications, a new thermal model for high-temperature MW ablation is proposed and expressed as:Where H(T)(W/m³) is the energy needed to vaporise water as a function of temperature (T), and (W/m³) is the rate of heat generation that is a piecewise function of temperature (T).

We have validated simulation results that are based on this thermal model by comparing against measured temperatures in experiments with bovine liver tissue. A reasonable agreement between calculated and measured temperatures is obtained at points that are 0.5 cm and 1 cm in radial distance from the MW antenna (Figure 15). Some deviation between computer simulation and actual measured temperatures did arise, due to the fact that the thermo-physical properties in different liver tissue can vary. The temperature deviation between simulation and experiment is generally less than 5°C, however, and the simulation results that use the proposed modified thermal model are quite satisfactory (Table X) [20].

There are some shortcomings inherent in our study. First, the mapping between enthalpy and tissue water content only takes into account the instantaneous temperature, which in reality is likely to be a function of the temperature history. Second, we have only considered tissue water vaporisation, while other water movements such as water diffusion, water vapour diffusion, and condensation are not taken into account. Lastly, water vaporisation and tissue carbonisation needs to be verified in an in vivo experiment, which will allow for a better understanding of the heat transfer mechanisms in biological tissue during MW ablation at elevated temperatures.

Conclusion

It can be concluded that incorporation of enthalpy and the realistic, time-dependent SAR in a simulation of the MW heating of biological tissue improves the accuracy of the results for the temperature field, particularly near the MW applicator. A reasonable agreement between simulation results and experimental data has been obtained, wherein the maximum average deviation in the simulation from measurements is less than 5°C. A more realistic thermal model is one that should incorporate water vaporisation and subsequent tissue carbonisation. We have proposed a new modified model, which may be used for tissue temperatures where water evaporation is sure to occur. The present results may be useful in clinical MW ablation practice and can be applied to predict temperature field distributions for surgical planning purposes.

Further studies will analyse the effects of water vaporisation and tissue carbonisation in tissue in vivo.

Acknowledgements

The authors are grateful for the anonymous reviewer's constructive comments on this paper.

Declaration of interest: This research was supported by Beijing Nature Science Foundation grants 3072004 and 3112005, and also supported by National Nature Science Foundation of China grant 30770547. The authors alone are responsible for the content and writing of the paper.