Cylindrical agar gel with fluid flow subjected to an alternating magnetic field during hyperthermia

Abstract

Purpose: In magnetic fluid hyperthermia (MFH), nanoparticles are injected into diseased tissue and subjected to an alternating high frequency magnetic field. The process triggers sufficient heat to destroy the cancerous cells. One of the challenging problems during MFH is blood flow in tissue. In real conditions the heat which is transferred by blood flow should be considered in the analysis of MFH. Methods: In this study, heat transfer was investigated in an agar gel phantom containing fluid flow. Fe₃O₄ as a nano-fluid was injected into the centre of a gel cylinder which was filled with another gel cylinder and subjected to an alternating magnetic field of 7.3 kA/m and a frequency of 50 kHz for 3600 s. The temperature was measured at three points in the gel. Temperature distributions regarding the time at these three points were experimentally measured. Moreover, the specific absorption rate (SAR) function was calculated with a temperature function. Results: The SAR function was a key asset in the hyperthermia and was obtained on the condition that the fluid flowed through the gel. Finally, a finite element analysis (FEA) was performed to verify the SAR function. The results revealed that there was good agreement between the measured temperature and the one obtained from FEA. In addition, the effects of fluid flow and accuracy of function obtained for heat production in the gel were presented. Conclusion: It is believed that the proposed model has the potential ability to get close to reality in this type of investigation. The proposed function has implications for use in further modelling studies as a heat generation source.

• Flow
• hyperthermia
• magnetic nanoparticles
• SAR function
• specific absorption rate

Introduction

Although normal body temperature is 37 °C, many of the body’s cells can survive in temperatures up to about 42 °C. Hyperthermia therapy methods raise cell temperatures in the range of 42–45 °C to eliminate tumour cells. The temperature range was recommended for the following two reasons, 1) the cancer cells would be destroyed at temperatures above 42 °C, and 2) at less than 45 °C possible side effects can be controlled. Hyperthermia therapy methods nowadays are used in cancer treatment in addition to other treatment methods such as radiotherapy and chemotherapy. The reason is that in many cases these treatments are not fully capable of destroying cancerous cells. Moreover, cancerous cells are more vulnerable to high temperatures, and consequently hyperthermia therapy should invoke better outcomes [1].

A synergistic interaction between heat and radiation has been validated in preclinical studies [2,3]. This method is effective even in temperatures below 41 °C. Hyperthermia treatment is at its most effective when provided at the same time or within an hour of radiation [4]. As found in preclinical experiments, the time between treatments and the sequence of operations is important [5].

Strategies to improve radiotherapy are aimed at increasing the effect on the tumour or at decreasing the effect on normal tissues, which must be achieved without sensitising the normal tissues in the first approach and without protecting the tumour in the next approach. Hyperthermia is a potent sensitiser for cell killing by ionising radiation (IR), which can be attributed to the fact that heat is a pleiotropic damaging agent, affecting multiple cell components to varying degrees by altering protein structures, thus influencing the DNA damage response [4].

Several types of interaction of heat with chemotherapeutic drugs have been found [6], such as supra-additive (alkylating agents, platinum compounds), threshold behaviour (doxorubicin), and independent or additive (fluorouracil, taxanes, and vinca alkaloids). The synergistic effect in vitro can be several powers of ten even at moderate temperatures (e.g. for cisplatin) [7].

Gilchrist suggested using magnetic materials with hyperthermia in 1957 [8]. Nanoparticles in this method must have superparamagnetic or ferro and ferromagnetic properties. This type of nanoparticles keep their magnetic properties even when there is no external field [9] and superparamagnetic nanoparticles are ideal candidates for hyperthermia cancer treatment. Fe₃O₄ was the first magnetic nanoparticle subjected to a magnetic fluid. Preparing this solution for the first time was conducted by NASA in 1960 [10,11].

Due to safety issues for living creatures, study on living tissue is not always possible. Hence, investigation of hyperthermia needs an appropriate environment similar to living tissue [12]. Another problem in experiments on living creatures is accurate temperature measurement, particularly in the context of border (all tissues, including tissue, tumor). Difficulty in observing the exact distribution of nanoparticles in living tissue is another factor that may encourage researchers to employ other environments. Recent studies have revealed that the porosity of agar gel is similar to living tissue, and as a result it can be used as an ideal environment for drug delivery testing [13–18]. It has been reported that gel is a substance between liquid and solid that contains a solid matrix and water holes [19]. Different concentrations of gel can simulate different tissues. In many cases gel material has been used to simulate drug delivery in real tissue [20–24]. As part of our study, nanoparticle diffusion rates and their orientation in a porous structure have been studied [25]. Salloum et al. [26] showed that the diffusion rate can be predicted in real tissue.

Another application of gel is in cell culturing, where Arum et al. [27] cultured a known number of cancer cells in gels and then the number of cells destroyed after performing hyperthermia was counted. Lee et al. [28] investigated the hyperthermia process and microscopic structure in a uniform medium of gel and nanoparticles. Heat transfer in a two-layer cylindrical gel inner and outer ring representing tumour tissue and healthy tissue, respectively, was studied by Rahn et al. [29].

Software simulation and coding techniques have been employed to solve the problem of heat transfer for various methods of hyperthermia. Numerical methods such as the finite difference method, finite element and boundary element have been used in many studies to simulate heat transfer in hyperthermia using magnetic fluid. A numerical solution for the bioheat transfer equation in spherical coordinates was given by Lin and Liu [30]. Zhang et al. [31] showed a solution for the bioheat transfer equation in a multi-layered environment. Pavel et al. [32] calculated an optimised nanoparticle concentration. Sou et al. [33] found the effects of some parameters related to the injection of nanoparticles. They calculated temperature distribution for a variety of nanoparticle diffusions, needle diameters, and tissue elasticity. A bioheat transfer equation in a cylindrical coordinate was solved by Gupta et al. [34]. Andra et al. [35] analytically derived spatial temperature distribution as a function of time for exposure to an alternating magnetic field. They developed their assumptions for small tumours in relatively homogeneous tissue with low blood perfusion.

Under real conditions blood flow transfers the heat generated by the nanoparticles in real tissue. Hence, in the absence of fluid flow temperature increment is greater. Fluid flow is often not considered in case studies used for gel, and heat transfer alone has been reviewed for various injection modes. In addition, specific absorption rate (SAR) function has not been introduced for gel with fluid flow. In this study, an experimental set-up was established that provided more realistic conditions by adding fluid flow to the gel. Although water was used as fluid, a good estimation of temperature rise similar to real conditions was obtained. This claim was validated by using finite element analysis (FEA). Measured temperature introduced a SAR function that was used as a heat source in the finite element method (FEM) to give temperature distribution. This process can show the real heat which is generated in testing samples.

Materials and methods

Experimental part

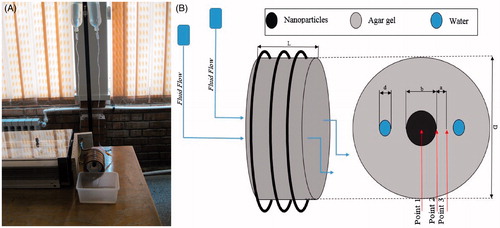
In this research, hyperthermia (YK2005RH real time data logger with K type sensor) was performed on two concentric gel cylinders (Cylinder dimensions are given in Table 1. Water, agar powder and PL-M-Fe₃O₄ have been used. Agar powder was provided by Parsian Shimi Co. Mean diameter of nanoparticles was 8 nm and was made by Plasmachem GmbH). The inner cylinder, diameter b, contained a mixture of gel and nanofluid; the outer cylinder diameter was D and the gel included two pathways for water flow. The sample was placed into a polymer plastic shell with length L. The inner cylinder contained a mixture of 3.5 cm³ gel and 0.5 cm³ nano-fluid. To prepare this sample, after solidification of outer cylinder, the nanoparticle and gel mixture was poured into it as the inner cylinder (To do this, an obstacle cylindrical shape as inner cylinder was used (imagine an annular container for outer part). After solidification the obstacle was removed). To prepare the inner cylinder, which was a combination of gel (3% hydrogel, Parsan Shimi Co., Tehran, Iran) and nano-fluid, nanoparticles (two water serums, each one for water flow for each pipe) were added to the gel at 60 °C. The experimental set-up and its schematic are indicated in Figure 1. Two serum transfusions were placed at a height to maintain water flow. This test was conducted under the assumption that the fluid temperature was constant and equal to 20 °C. Water flowed inside two pipes with internal diameter d through gel. Water velocity inside the plastic pipe with very thin thickness was controlled by a serum valve and was maintained at a constant rate of w in the whole experiment. Properties and parameter values are presented in Table 1.

Figure 1. (A) Experimental set-up and (B) its schematic with parametric dimensions.

Table 1. Parameter values.

Parameter	Value
D	60 (mm)
L	32 (mm)
d	5 (mm)
b	15 (mm)
a	3.75 (mm)
w	0.45 (mL/s)

D, L, d, b, a and w are outer cylinder diameter, cylinder length, diameter of fluid flow canal, point of temperature measurment respect to inner cylinder wall and volumetric flow rate, respectively.

In this experiment Fe₃O₄ nano-fluid was used at 3% volume concentration, and the diameter of the nanoparticles was 8 nm. According to clinical reports, the volume percentage of nanoparticles permitted is 3% [36]. Gel, magnetic nanoparticles and the mixture of nano-fluid and gel properties are listed in Table 2. In this table ρ, k, and c were material density, heat conduction coefficient, and specific heat capacity, respectively.

Table 2. Experimental material properties.

Material	ρ (Kg/m^3)	k (W/mK)	c (J/kgċK)
Nanoparticles	4950	60	670
Gel	1000	0.566	3900
Gel-nanoparticles mixture	1015	0.566	3888

ρ, material density; k, heat conduction coefficient; c, specific heat capacity.

Gel and nanoparticles mixture properties can be calculated as follows [30]: (1) (2) (3) where φ, ρ, and c are nanoparticle volumetric percentage, density, and specific heat capacity, respectively. In the above equations gel, np, and sample subscripts refer to gel, nanoparticles and mixture properties, respectively. Although many studies have been carried out to calculate heat conduction coefficients, because of low nanoparticle volume in gel and low temperature increments, the heat conduction coefficient of agar gel was considered as the heat conduction coefficient of the sample [37].

The sample was subjected to a field with frequency of 50 kHz and intensity of 7.3 kA/m for 60 min. Temperature was measured at 300, 600, and every other 600 s (YK2005RH data logger with K type sensor). Temperature measuring points were at a depth of 15 mm from gel surface and are shown in Figure 1.

Specific absorption rate

SAR is the rate at which the human body tissue absorbs energy when applying an external force. This external force is energy generated by an electric field, electromagnetic waves or ultrasound waves. In this study SAR is the amount of heat produced by the simulated body tissue in magnetic fluid hyperthermia measured in W/m³.

Since the only heat source was magnetic nanoparticles and the only heat absorber was gel, SAR was considered to be heat generation. To obtain the SAR, the slope of the temperature versus time at t = 0 is needed. The SAR at any point was calculated as in Equation 4(4) [26,37]: (4)

Table 2 shows C_gel and ρ_gel values. In the current study a function has been considered for experimental measurements and used to calculate the SAR.

Specific absorption rate verification

A FEA was performed to verify the function obtained for the SAR.

Problem physics

The temperature distribution equation was solved and SAR was considered as a heat generation term (Equation 5(5) ) (5) where Q_s (W/m³) was the heat generated by nanoparticles which is a SAR, Q_fluid was the removed heat rate by the fluid flow that can be expressed as a cooling source (Equation 6(6) ) (6) where m (kg/s), C_p, T_fluid, T, and V_tube are mass flow rate, fluid specific heat capacity, fluid temperature, gel temperature at any time point, and pipe volume inside gel, respectively. Water at 20 °C was used as fluid inside the pipes.

Geometry and boundary conditions

A 3D cylindrical model was used for simulation. According to the ambient temperature, a convection heat transfer with a heat transfer coefficient equal to 10 W/m²K was used for all of the boundaries. Initial temperature was 20 °C.

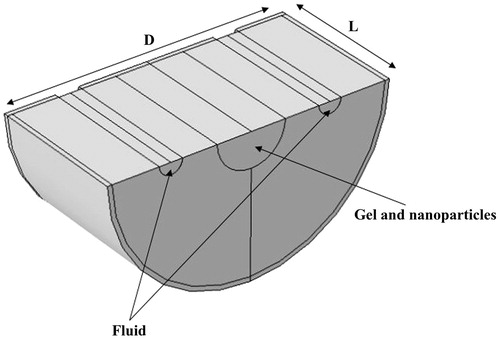
Figure 2 shows the geometry used for modelling. To reduce the computational time, symmetry was assumed on the upper part of the geometry (Figure 2). Each part, i.e. gel, gel and nanoparticle mixture, and water flow path, has been shown.

Figure 2. Geometric model of the gel and fluid.

Mesh

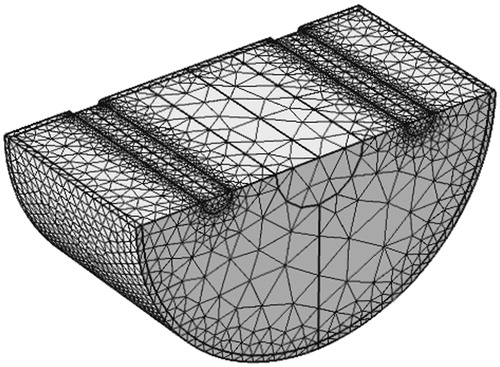
The mesh generated is shown in Figure 3. Several levels of mesh refinement were examined, i.e. coarse, intermediate and fine meshes. The intermediate mesh gave satisfactory results without considerable difference in temperature compared to the fine mesh. For an intermediate level of mesh refinement the mesh was composed of 54 575 elements.

Figure 3. An unstructured mesh of the whole domain.

Results

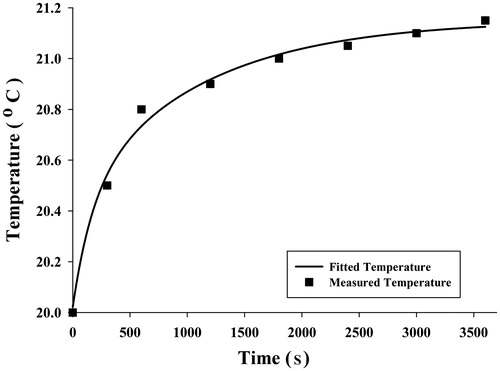
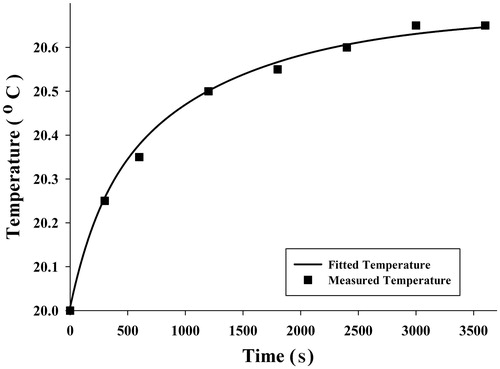
An appropriate temperature versus time function was used to obtain SAR function at each point. Since average temperatures measured were obtained for three points in three experiments and for each point 8 times, it was possible to fit a curve to these eight points to achieve a desirable temperature function. A five-parameter exponential function was chosen to describe the time-dependent temperature distribution: (7) where a, b, c, d, and e are constant and differ for each gel point. The parameter values for each point are reported in Table 3.

Table 3. The estimated parameter values for each point.

	Estimated parameter values
Points	a	b	c	d	e
1	20.0221	0.4319	0.0057	0.6971	0.0009
2	20.0078	0.2289	0.0049	0.4344	0.0008
3	9.9886	0.1888	0.002	0.2178	0.0005

a, b, c, d and e are the constants of used function in the context.

Although other functions of exponential type had the ability to estimate the temperature distribution, the five-parameter function can describe the temperature distribution with the least difference compared to the measured temperature. The average measured temperature value at each time and selected functions have been shown in Figures 4, 5 and 6.

Figure 4. The average of measured temperature at point 1 and the estimated curve for these points.

Figure 5. The average of measured temperature at point 2 and the estimated curve for these points.

Figure 6. The average of measured temperature at point 3 and its estimated curve for these points.

According to Equation 4(4) and using Equation 7(7) , time differential at t = 0, SAR would be: (8) (9)

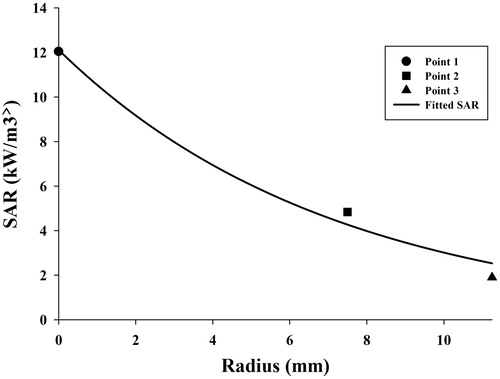
Using Equation 9(9) and values given in Table 3 for each measuring point of the gel, SAR was obtained. To estimate an appropriate function which showed SAR at a different radius of the gel, three SAR for three measuring points were calculated. SAR values for each point and the exponential curve which was well fitted with the points are indicated in Figure 7.

Figure 7. Specific absorption rate (SAR) value for each point and the related fitted curve.

An exponential function which was used to estimate SAR versus radius is shownin Equation 10(10) (10) where r mm is the radial distance from central axial, parameters of a and b are equal to 12.1146 kW/m³ and 0.1391 1/mm, respectively.

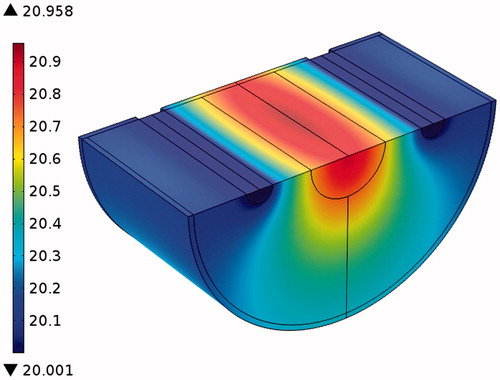
To validate SAR function, FEA by software simulation was used. SAR was considered a heat generation term in the heat transfer equation, and temperature distribution was obtained to compare with temperatures measured. Figure 8 indicates temperature distribution in the radius direction and temperatures at three points of the gel which were obtained by FEA and experiment at 3600 s, respectively. It seems that the curve is well fitted with the temperatures measured. To show how temperature rose in all parts of the sample, especially near the fluid path, temperature contours at 3600 s obtained by FEA are shown in Figure 9.

Figure 8. Radial temperature distribution and temperature measured at points 1, 2, and 3 with curve fitted to these points.

Figure 9. Temperature contours (°C) at t = 3600 s.

Discussions

This study aimed to create a more realistic experimental condition using heat generated by nanoparticle transfer with blood flow. Thus water as a fluid was flowed through two pathways to cool the gel simulating blood flow. Although the physical properties of blood and water are completely different, it was a reasonable assumption to use water to simulate the cooling effect of blood flow. In most of the previous studies, body and blood temperature were assumed to be 37 °C before hyperthermia treatment. After hyperthermia the heat produced increases the body temperature while the blood stays at a constant temperature. In the experiment both gel and water were initially at 20 °C and the water stayed at a constant temperature while the gel temperature increased.

Results showed that the temperatures measured at three different points during 3600 s were in good agreement with expectations. Similar to claims by Salloum [26] and Rahn et al. [29], regions with more nanoparticle concentration achieved higher temperatures. Figures 4–6 illustrate that point 1 had more temperature increments, which we believe to be related to the nanoparticle concentration at this point. However, the maximum temperature at point 1 is not as high as the temperatures obtained by the analytical [31,35] and numerical [32–34] studies of Pennes’ bioheat transfer equation. Moreover, some experimental studies on gel [26,29] have reported higher temperatures by nanoparticle concentration and magnetic field as with this study, but some important factors prevent high temperatures. The most important factor causing slight temperature increment was water flow in the gel. This difference in the temperature occurs as a result of fluid flow and was the main focus of the study, to provide more realism. The other factor is the amount of injected nanoparticles allowable for use in real clinical situations to prevent damage to the body. In these circumstances a large amount of the heat generated is absorbed by the gel. Another contributing factor might be related to the low frequency of the device. Diagrams of temperature versus time shown in Figures 4–6 are well in agreement with the measured temperatures and initial large temperature initial slope.

It has been reported that SAR has an exponential function [26]. As expected, the amount of heat generated in the cylinder centreline is the greatest, and decreases in a radial direction. SAR obtained from an experimental study is useful for computer simulation or analytical solutions for optimisation problems. The advantages of SAR obtained in this study were consideration of fluid flow and validation.

As already mentioned, the water was at a constant temperature of 20 °C. It can be a suitable assumption for this kind of experiment that temperature was not significantly increased. Figure 9 shows the temperature distribution and a higher temperature was produced below the inner cylinder where no fluid flow was contained. This phenomenon is acceptable in this condition, however, for a higher temperature produced by higher nanoparticle concentration or field strength can destroy the blood vessels in the body [38–41]. In fact, the arrangement of fluid paths disturbed the symmetry that was shown in the temperature distribution [29,31,32].

Conclusion

This study tried to approximate real tissue and heat generation obtained with nanoparticles in experimental medium conditions. Two pipes were placed through the gel medium to simulate blood flow and investigate the transfer of heat by fluid in hyperthermia therapy. Nanoparticles of FE₃O₄ were injected into the centre of a gel cylinder and placed inside a magnetic field with 7.3 kA/m intensity and 50 kHz frequency for 3600 s. SAR was calculated for three different locations. Computer simulation was carried out and temperature distribution inside the gel was compared to the experimental data. This study proposed an experimental set-up to add fluid flow to the gel environment, and verification of this process to give an accurate SAR function was presented as well. In future it will be possible to use blood instead of water and place a blood source at an appropriate height to provide realistic blood pressure in the body. In addition, a heat exchange system can be added to maintain the temperature at 37 °C.

Acknowledgements

The authors would like to thank staff of the Tissue Engineering and Biological Systems Research Laboratory, School of Mechanical Engineering, Iran University of Science and Technology (IUST). The authors also gratefully acknowledge the Cancer Research Center of Tehran University of Medical Sciences especially Dr Saeid Amanpour for his great collaboration with Iran University of Science and Technology.

Declaration of interest

The authors gratefully acknowledge funding of this research by the Iran University of Science and Technology. The authors alone are responsible for the content and writing of the paper.