Simulations of the c-subunit of ATP-synthase reveal helix rearrangements

Abstract

The c-subunit of the enzyme, ATP synthase couples the proton movement through the a-subunit with its own rotation and subsequent rotation of the F1 ring to drive ATP synthesis. Here, we perform μs time-scale coarse-grained molecular dynamics simulations of the c-subunit to characterize its structure and dynamics. Two different helix-helix interfaces, albeit with similar interfacial characteristics, are sampled in the simulations. The helix-2 of the c-subunit monomer rotates around the axis of helix-1 bringing about a change in the interface. Previous models have also proposed such a change in the helix interface but postulated that helix-2 swivels around its own axis. Such large-scale changes in helix packing motifs have not been observed before. The helix-swirling persists even in the c-subunit ring but the dynamics is much slower. The cooperative behavior in the ring appears to stabilize a conformation less-populated in the monomer. Analyzing the stability of the c-subunit ring, it was found that six lipid molecules are necessary to fill the central cavity of the ring. These lipid molecules were not aligned with the surrounding bilayer but protruded towards the periplasmic side. The characterization of the monomer and ring presented in this work sheds light into the structural dynamics of the c-subunit and its functional relevance.

Keywords::

• Coarse-grain simulations
• helix swirling
• molecular dynamics
• MARTINI Force Field

Introduction

ATP synthase is an enzyme that converts transmembrane proton gradients in eubacteria, chloroplasts and mitochondria into chemical energy that is then stored as ATP [10,17]. The enzyme consists of two coupled rotary motors: The membrane-embedded F_o and the solvent-exposed F₁. F_o is composed of three types of subunits, a₁ b₂ c_10-15 [21], and F₁ of five subunit types, α3 β3 γ1 δ1 ϵ1 [1,21]. The subunit c of F_o is known to form an oligomeric ring of 10 or more subunits [25,44,51,52] and subunits α and β of F₁ a hexameric ring of alternating subunits [16,32]. Current models postulate that protons are translocated across the membrane through subunit a [3,4,18] that is in contact with the c-ring [24]. The c-ring couples the proton movement through the a-subunit to its own rotation and a cycle of alternating protonation/deprotonation of an aspartate residue [58]. Rotation of the c_10-15 ring is also coupled, through γ ϵ subunits [7,26,56] to the rotation of the F₁ ring that drives the synthesis and release of ATP [1,9,16,22,32,40,41,47,48]. The structure of F₁ and the basic mechanism of ATP synthesis by F₁ are now well established, but the structural characteristics of F_o and how proton translocation through it drives these catalytic changes is less clear [19].

Structural data from Escherichia coli and Bacillus PS3 [25,38,53], Ilyobacter tartaricus [52], chloroplasts [50] and Spirulina platensis [44] indicate that subunit c forms rings with 10, 11, 14 and 15 monomers per complex, respectively. The internal cavity of the c10−15 ring has been suggested to be filled with lipids, though direct evidence is absent [30]. High resolution crystal structures have been determined for the c-subunit ring of I. tartaricus [31], chloroplast [60] and a related V-type ATP synthase from Enterococcus hirae [37] and a low resolution structure for yeast mitochondria [53]. The data shows that subunit c folds as a helical hairpin within the membrane with the loops of the subunits in the cytoplasm and the termini in the periplasm. The ring looks like a hourglass-shaped cylinder consisting of a tightly packed inner ring comprising of the N-terminal helices (helix-1) and an outer ring where the C-terminal helices (helix-2) pack into the grooves formed by the inner helices [31,53,60]. A number of structural models based on NMR experiments and cross-linking data have also been proposed for E. coli [15,20], Propionigenium modestum [29], and bacillus PS3 [38]. Analysis of the NMR structure of E. coli, shows that the two helices of the c-subunit monomer pack as a right-handed anti-parallel pair. Such a packing pattern has been recently found to be abundant in transmembrane proteins but has not been studied extensively [61]. The helix-packing in E. coli is however incompatible with the I. tartaricus structure and the two structures differ in the helix-helix interface. This motivated a recent study by Vincent, Fillingame et al. and their results postulate that helix-2 swivels around its own axis resulting in an inter-conversion of the two helix-helix interfaces seen in the E. coli and I. tartaricus structures [59]. The possibility of two different interfaces in the helix-turn-helix structure of the c-subunit of the ATP synthase of E. coli makes it an unusual protein since membrane proteins are usually considered to associate only via a given interface, defined by the residues whose mutation causes disruption of association.

The interactions that affect the formation of c10−15 rings in the ATP synthase complex leading to the above-described structures are also not well characterized. Walker and co-workers reported that subunit c in E. coli self assembles into annular structures in the absence of other subunits of the complex [5], suggesting that the ability of recombinant subunit c to form rings is specfied by its amino acid sequence. Müller et al. showed that in I. tartaricus and spinach chloroplast the cylindrical transmembrane rotors of ATP synthase occasionally exhibit structural gaps of the size of one or more subunits and that the incomplete rings have the same diameter of the complete ones [35]. Their results suggest the rotor diameter and stoichiometry are determined by the shape of the subunits and their nearest neighbor interactions. Two mutants of subunit c of E. coli, G23D and L31F, have been shown to be defective in assembly of the F_o sector [23]. A recent study investigating this mechanism deeper demonstrated that the protein YidC is required for the insertion of these mutants into the membrane, but, once inside, they still fail to assemble [27]. Further studies are needed to understand the mechanism responsiblefor the assembly failure.

Molecular dynamics simulations have proven useful in the absence of sub-molecular level data and simulations of F_o subunit have been reported. Krilov and co-workers investigated the structure of the c-subunit monomer in lipid bilayers as well as in membrane mimetic mixtures commonly used in experimental measurements and showed that the structure and flexibility of the monomer differs in the two media [34]. Schulten and co-workers used steered molecular dynamics simulations and mathematical modeling to investigate the mechanism of torque generation in F_o [2]. They proposed a model that coupled swivelling of helix-2 to protonation/deprotonation of the residue Asp-61 to drive the rotation of the c-subunit ring.

Investigation of the long-time scale dynamics of the c-subunit ring in the membrane environment by atomistic simulations is still challenging. To access these larger time and length scales, coarse-grain models have been used successfully, especially in probing lipid mediated protein interactions [11,14,43,45]. In this paper, we present the results of coarse-grain molecular dynamics simulations of c-subunit of E. coli in a palmitoyl-oleoylphosphatidylethanolamine (POPE) bilayer and water. The MARTINI Force Field is used to describe the coarse-grain protein, lipid and water particles [28,33]. The monomeric c-subunit, as well as the whole ring structure were simulated at a μs time scale. We characterize the large scale dynamics in the c-subunit monomer and propose an alternate model to the swivelling of the helices. We also compare the swivelling movement in the c-subunit monomer and in the ring. The number and position of the lipids in the central cavity of the c₁₀ ring is also studied.

Methods

Force-Field

The MARTINI lipid Force Field [28] was used to describe the coarse-grain lipid and water particles. A pre-release version of the MARTINI protein Force Field [http://md.chem.rug.nl/marrink/coarsegrain.html] [33] was used to describe the peptide particles. The MARTINI Force Field is a coarse grained Force Field that is based on a four-to-one mapping, i.e., on average four non-hydrogen atoms are represented by a single interaction center. The Force Field has been parametrized based on the reproduction of partitioning free energies between polar and apolar phases and allows an accurate representation of the chemical nature of the underlying atomistic structure. In this Force Field, the backbone parameters (backbone-bonded terms) are dependent on the secondary structure of the beads but independent of the amino acid. To maintain the coarse-grain model in the starting secondary structure, distance constraints between backbone atoms (every first and fourth for α-helical conformations) are added. It has been successfully applied to describe lipid-protein interactions [6,11,12,43,49,54,55,62].

Simulation parameters

The molecular dynamics simulations were performed using the GROMACS program package [57], with the scheme developed for coarse-grain simulations, under periodic boundary conditions. The temperature was weakly coupled (coupling time 0.1 ps) to a thermostat at T = 300 or 325 K using the Berendsen algorithm to investigate the dynamics at the different temperatures [8]. The pressure was also weakly coupled (coupling time 1.0 ps, compressibility 5 × 10⁻⁵bar⁻¹) using a semi-isotropic coupling scheme, in which the lateral and perpendicular pressures are coupled independently at 1 bar [8]. The non-bonded interactions were treated with a switch function from 0.0–1.2 nm for the Coulomb interactions and 0.9–1.2 nm for the LJ interactions (pair-list update frequency of once per 10 steps). A time step of 35 fs was used. The simulation times reported in the manuscript are effective times obtained by the multiplication of the actual simulation time by a factor of four based on the speed-up achieved for diffusion of water and lipids [28,33].

System set-up

The decameric ring and the individual monomer of c-subunit of E. coli ATPsynthase were simulated. In both systems, the amino-acid residues 5–37 (helix-1) and 50–77 (helix-2) were constrained to be α-helical.

Monomer

Two different monomer structures were simulated: a monomer from the PDB (1c0v [15]) and a monomer from the end of a short 2 ns atomistic simulation [2], both mapped to their coarse-grain representation (see Table 1 for overview of simulations). The two structures deviate from each other with a root mean square deviation (RMSD) of 0.3 nm (for all backbone beads). The secondary structure of both the monomers was defined as before. The monomers were inserted in pre-equilibrated POPE bilayers with a lipid to peptide ratio of 180:1 and 7000 water molecules.

Table I.  Overview of MD simulations performed. The c₁₀-ring and a single monomer were simulated. Two starting structures were simulated – the NMR structure (PDB code 1C0V [15,20]) and an equilibrated structure from a 2 ns atomistic simulation [2]. Simulations were performed at different temperatures to increase sampling. The times reported here are effective times [28,33].

No.	System	Starting structure	Temperature	No. of simulations	Total simulation
1a–d	Monomer	atomistic simulation	300	4	240 μs
2a–d	Monomer	atomistic simulation	325	4	180 μs
3	Monomer	1C0V NMR structure	325	1	14 μs
4a–d	Ring-6 lipids	Model from 1C0V	325	4	40 μs
5a,b	Ring-4 lipids	Model from 1C0V	325	2	5 μs

Ring

The atomic structure of the c10-subunit ring was taken from the structure modeled from the biochemical data and the monomer structure above [2,19]) and mapped to its coarse-grain representation. The ring was inserted in a pre-equilibrated POPE bilayer with 384 lipid molecules and about 5500 coarse-grain water particles. Two different setups, containing 4 or 6 POPE molecules in the central cavity, were tested (see Table 1 for overview of simulations).

Analysis

Comparison of coarse-grain and atomistic structures

The root mean square deviation, RMSD of the backbone beads of the equilibrated coarse-grain structure was calculated with respect to the ca atoms of the atomistic structure. The backbone beads of the two helical stretches (residues 5–37 and 50–77) were fitted separately.

Helix parameters

The helix axis was defined as the axis joining the backbone atoms of the residues 6 and 36 in the long helix and 51 and 75 in the short helix. This simple method does not accurately describe the helix axis but is adequate for calculating the changes in cross-over angle in coarse-grain models, especially in the presence of secondary structural constraints. The cross-over angle was calculated as the angle between the two helix axes for both the coarse-grain and atomistic structures. The z-shift of each helix was calculated as the shift of the center of the helix along the membrane normal with respect to the center of the two helices.

Monomer parameters

The residues at the helix-helix interface of the monomers were defined as those with a minimum distance of less than 0.5 nm from their backbone bead to the backbone of the other helix. The monomer-monomer distance in the dimer was defined as the minimum backbone-backbone distance between the two monomers.

Reaction coordinate for helix swirling

The helix-helix rotation in the c-subunit monomer was defined by a linear coordinate distinguishing interface 1 (characterized by residue 20) and interface 2 (containing residue 21). The difference of the minimum distance between the residue 20 and the backbone of helix-2 and residue 21 and the backbone of helix-2 was calculated. A positive value indicates interface 1 and a negative value interface 2.

Cluster analysis

The conformations of the c-subunit were clustered using the Daura et. al. algorithm [13] using a cut-off of 0.2 nm.

Diffusion constants

The diffusion constants were calculated by fitting to the mean square displacements of the monomer and ring in the simulations.

Results

C-subunit monomer

Comparison of atomistic and coarse-grain structures

The coarse-grain model of the c-subunit of E. coli in a POPE bilayer with surrounding water is shown in Figure 1. As a test of the model, short time-scale (ns) simulations of the system were compared to atomistic simulations of the c-subunit monomer [2]. In the MARTINI coarse-grain Force Field, constraints (dihedral or distance) that impose ideal helicity reduce the conformations that helices can sample and may prevent them from kinking and bending. To investigate the effect of secondary structural constraints (imposed by the Force Field), the coarse-grain structure was compared to the equilibrated atomistic structure (mapped to coarse-grain). The RMSD of the backbone beads of the helices in the two structures is low – 0.15 nm and 0.19 nm for helix 1 and 2, respectively, thus validating the use of distance restraints to represent the transmembrane domains of the c-subunit as ideal helices.

Figure 1.  The structure of the c-subunit of ATP synthase. (A) The coarse-grain representation of the c-subunit monomer in a POPE bilayer with surrounding water. (B) A pictorial description of the helix-helix interfaces (interface-1 and 2). The helices are rotated by 90° around the membrane normal with respect to Fgure 1A and 1C. Interface-1 is characterized by the residues Ala-13, Met-16, Ala-20, Ala-24, (Gly-27) Ile-28, Leu-31 in helix-1 and Thr-51, Phe-54 (Ile-55), Gly-58, Ala-62, Ile-66, Gly-69, Tyr-73 in helix-2. The residues characterizing interface-2 are Tyr-10, Ala-14, Met-17, Ala-21, Ala-25, Ile-28, Gly-29, Gly-32 in helix-1 and Thr-51, Phe-54, Gly-58, Ala-62, Ile-66, Gly-69, Tyr-73 in helix-2. (C) A pictorial description of the two states sampled in the simulations. State-1 is characterized by a low cross-over angle and state-2 with a large cross-over angle. This Figure is reproduced in colour in Molecular Membrane Biology online.

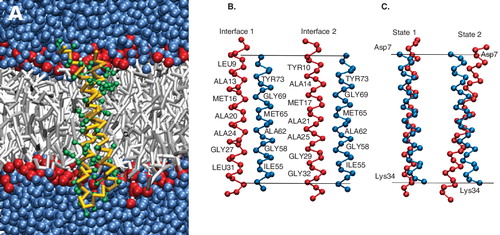
Comparing the simulations of the monomer, it is observed that the right handed anti-parallel packing motif is maintained in both atomistic and coarse-grain simulations. The simulations in Ref. [2] were reanalyzed for the cross-over angle. The equilibrated cross-over angle is similar for both structures: 15° for the atomistic structure and 12° in the coarse-grain model. The minimum distance between the backbone beads (C_α for the atomistic structure) in the two helices (inter-helical distance) is 0.48 ± 0.02 nm in the equilibrated coarse-grain structure and 0.48 ± 0.06 nm in the atomistic simulation. The helix-helix interface was also maintained in the equilibrated coarse-grain structure. This interface, referred to henceforth as interface-1, is shown in Figure 1. The interface is characterized by the residues Ala-13, Met-16, Ala-20, Ala-24, (Gly-27) Ile-28, Leu-31 in helix-1 and Thr-51, Phe-54 (Ile-55), Gly-58, Ala-62, Ile-66, Gly-69, Tyr-73 in helix-2.

Helix swirling occurs in the c-subunit monomer

The μ-second time scale accessible by the coarse-grain simulations revealed large structural dynamics of the c-subunit monomer. The main motion characterizing the monomer is a ‘swirling’ motion, i.e., a rotation of one helix with respect to the other. The helix swirling dynamics occurred at μ-second time-scale and resulted in a change in the helix-helix interface. A second interface, referred to as interface-2, was sampled and is depicted in Figure 1. The residues characterizing interface-2 are Tyr-10, Ala-14, Met-17, Ala-21, Ala-25, Ile-28, Gly-29, Gly-32 in helix-1 and Thr-51, Phe-54, Gly-58, Ala-62, Ile-66, Gly-69, Tyr-73 in helix-2 (identical to interface-1). Comparing the two interfaces, it can be seen that, though helix swirling changes the residues of helix-1 at the interface, it does not change the characteristics of the interface substantially. The residues Ala-13, Met-16, Ala-20, Ala-24 in interface-1 are replaced by residues Ala-14, Met-17, Ala-21, Ala-25 in interface-2 and thus the residues at the center of interface-2 are identical to interface-1. Here we would like to point out that although the effect of the interface-change is a net rotation of the two helices with respect to each other, helix-1 does not actually rotate around its helical axis. Such a rotation would introduce a large strain in the loop region. Instead, helix-2 moves around the helix-1 axis to interact with a different interface of helix-1. What causes this swirling motion is not clear, but the characteristics of the interfaces points to comparable energies of the two states.

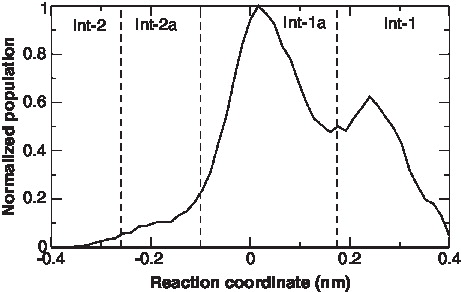
The change of the interface over time is shown in Figure 2A and B. The definition of the reaction coordinate used for the helix swirling is given in the methods section. A positive value indicates interface 1 and a negative value interface 2. The change of interface takes place at a μ-second time scale. The relative population of the two interfaces at 300 K and 325 K is plotted in Figure 3. At 300 K, interface-2 is the most frequented state, while at 325 K interface-1 is more populated. From Figure 3, it appears that interface-1 and interface-2 can be subdivided into two further interfaces – interface-1a and interface-2a. The residues at the interface of the two new interfaces, interface-1a and 2a are similar to interface-1 and 2, respectively. However, the interfaces differ in the actual inter-residue distances. The presence of interface 1a and 2a are easily seen in the time-course event shown in Figure 2A. Though interfaces 1a and 2a are low-populated at both 300 K and 325 K they appear not to be high-energy intermediates between the interface-1 and 2, but representative of local minima. It is interesting to note that the interface-1a is compatible with the NMR structure [20]. The free energy difference between Interface 1/1a and 2/2a can be estimated from the populations of the four interfaces. At 300K, ΔG = −1.4 ± 1.0 kJ/mol and at 325K, ΔG = 2.0 ± 0.5 kJ/mol.

Figure 2.  Time-dependent behavior of the different conformations of the c-subunit of ATP synthase at 300K. (A) Reaction coordinate showing interface1, 1a, 2a and 2. The definition of the reaction coordinate used for the helix swirling is given in the methods section. (B) Zoom in of A. (C) The cross-over angle between helix-1and helix-2 in the c-subunit monomer. (D) The z-shift of each helix calculated as the shift of the center of the helix along the membrane normal with respect to the center of the two helices. This Figure is reproduced in colour in Molecular Membrane Biology online.

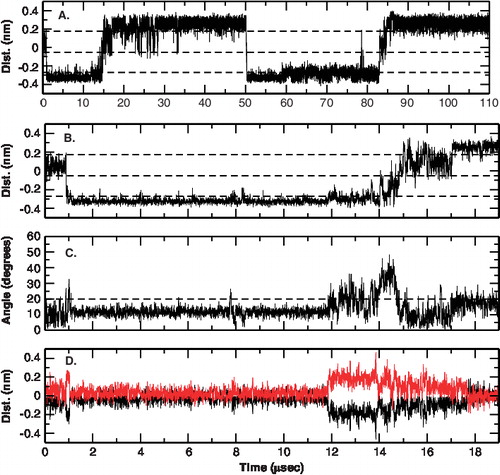
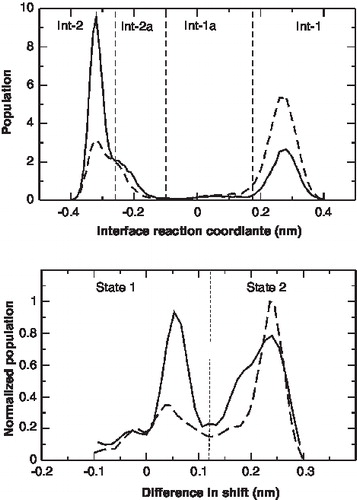
Figure 3.  Populations of the different conformations of the c-subunit. Top: The relative population of the four interfaces at 300 K(—) and 325 K(- - -). The normalized population of all the independent simulations is plotted. The definition of the reaction coordinate used for the helix swirling is given in the methods section. Bottom: The relative populations of the two states sampled at 300K (—) and 325K (- - -).

The cross-over angle of the c-subunit fluctuates

Long-time scale fluctuations in the cross-over angle of the two helices is also seen in the c-subunit monomer. The dynamics in both interfaces is similar and at first glance appears not to be correlated to the interface changes (but see below). At short time scales (up to 1 μsec), the cross-over angle is stable at around 12°. However, longer simulations revealed a change from the starting cross-over angle. In Figure 2C, the cross-over angle is plotted as a function of time. A two-state behavior is observed in which the cross-over angle changes between two states: 12° ± 5° and 25° ± 10°. Further analysis revealed that the change in cross-over angle is correlated to the packing of the helices. Figure 2D shows the shift of the center of mass of the two helices from the center of mass of the system. The same two-state behavior is observed. One state is characterized by the centers of the two helices close to the center of mass of the two helices and the cross-over angle around 12° (referred to as state 1). In the other state the relative position of the helices is shifted along the membrane normal and the cross-over angle is around 25° (referred to as state 2). This behavior is due to the presence of two charged residues: Asp-7 and Lys-34 in the helix 1. In state 1, residue Asp-7 lies in the aqueous phase, while residue Lys-34 lies at the interface of the head-group and membrane core environment, from where it snorkels outwards. In state 2, both residues Asp-7 and Lys-34 are surrounded by the polar head-groups of the lipids.

The two-state behavior persisted at higher temperatures (simulation 2) and in simulations with a different starting structure (simulation 3). A population of the two states at 300 K and 325 K (irrespective of the interface) is shown in Figure 3. At 300 K both states are equally populated whereas at higher temperatures state-2 is preferred. Atomistic simulations are unable to sample such long time scales and no such behavior has been reported. However, it is also possible that the secondary structural constraints impose such a behavior on the helices. In the coarse-grain model, the helices cannot deform to accommodate both the residues in the interface and such a see-saw dynamics may occur. Two indirect analysis support the feasibility of this behavior: The absence of large deviations from ideal helicity in the NMR structure and the absence of large-scale tilting in the coarse-grain simulations to achieve the same effect of accommodating the two residues at the membrane interface.

Correlation between the interfaces and states

Due to the low residence time in interface-1a and interface-2a along with the longer times required to equilibrate each of the interfaces after a conversion, it is diffcult to directly discern a correlation between the interface changes and the state changes from Figure 2. To map the structural characteristics of the interfaces sampled during the simulations, a clustering analysis was performed on the individual molecular dynamics trajectories. Four main clusters were visited in all simulations. The two largest clusters were compatible with interface 1 and 2. The other two clusters are low populated and correspond to interface 1a and 2a. Comparing the structural characteristics of the individual clusters, it is clear that interface-1 corresponds to state-2 (large cross-over angle) and interface-1a to state-1 (low cross-over angle). Similarly, interface-2 corresponds to state-1 (low cross-over angle) and interface-2a to state-2 (large cross-over angle).

c-subunit ring

Comparison to atomistic simulations

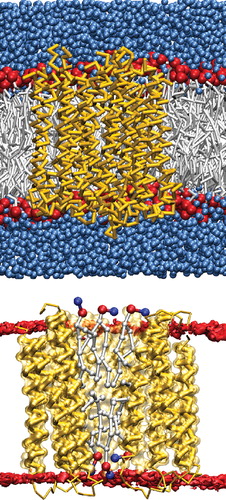
The coarse-grain model of the c-subunit ring in a POPE bilayer with surrounding water is shown in Figure 4A. The lipid molecules in the central cavity of the ring are shown in Figure 4B. The c-subunit ring was simulated at a μ-second timescale and was stable at these time scales. In order to compare to the atomistic simulation [2], we first focus on the initial nanosecond time-scale. The size of the c ring remained constant, with a radius of gyration of 1.95 nm. In the NMR structure of the c-subunit ring the monomers packed symmetrically, i.e., the same helices (helix-1:helix-1 and helix-2:helix-2) of the monomers associate. This dimerization pattern is maintained in the coarse-grain equilibrated ring structure. The starting interface of the individual monomers, interface-1 (Figure 1), is maintained in the simulation for all monomers. The cross-over angle was around 12° for nine of the monomers. Monomer-10 showed a higher cross-over angle to maintain the ring curvature, in line with the atomistic simulations.

Figure 4.  The coarse-grain representation of the c-subunit decameric ring. Top: A snapshot of the coarse-grain model with the backbone of the protein represented in yellow, lipid head-groups in red, lipid chains in gray and the surrounding water in blue. Bottom: A cross-section of the ring to depict the lipids in the central cavity (the phosphate beads are colored red and the nitrogen beads blue). This Figure is reproduced in colour in Molecular Membrane Biology online.

Dynamics is slower in the ring

Similar to the monomer, μ-second time-scale simulations of the c-subunit ring revealed large structural dynamics. An analysis of the interfaces sampled by the ten constituent monomers in the c-subunit ring is shown in Figure 5. Only three of the four interfaces seen in the monomer simulations are sampled in the ring. The populations of these interfaces also differ from the monomeric c-subunit. The most populated state in the ring is interface-1a that was low-populated in the monomers. This state is consistent with the NMR structure. The population of interface-1 is significantly lowered, and only one or two monomers populate interface-2a. The behavior persists in two independent simulations. Only two transitions from interface 1a to 1 or 2a were seen indicating a larger time spent in interface 1a. The changes in the interfaces of the adjacent monomers were not correlated. The populations of the two interfaces shown in Figure 5 cannot be considered representative of an equilibrium state since only a few transitions between the two interfaces were observed. The results are therefore still affected by the starting conformation (interface-1 in this case). Longer simulations are needed to give an estimate of the free energy difference between the two interfaces. Both states, 1 and 2 were sampled by the individual monomers. The population of state 1 (low cross-over angle) was high, consistent with the increased population of interface 1a. Comparing the populations and dynamics of the interfaces, it appears that the collective behavior of the c-subunit ring differs significantly from a single monomeric subunit.

Figure 5.  The relative population of the interfaces sampled by all monomers in the c-subunit ring. The definition of the reaction coordinate used for the helix swirling is given in the Methods section.

The lipids in the cavity of the ring protrude towards the periplasmic side

The number and position of lipids in the central cavity of the c-subunit ring of different species has been discussed [30,42]. In the absence of structural data, we performed two sets of simulations with 4 and 6 lipids in the central cavity of the c-subunit ring. The first set (two lipids in each leaflet in the central cavity) corresponded to the atomic simulations discussed earlier [2]. Though the c-subunit ring was stable at very short time scales, it collapsed to a flattened cylinder within 300 ns. Increasing the number of lipids to six (three lipids in each leaflet), thereby allowing better packing, the c-subunit ring remained stable and cylindrical. The increased number of lipids are in line with the evidence that 9–12 POPE molecules can be present in the cavity of the larger I. tartaricus c₁₁-ring [42]. However, in our study we test a symmetric arrangement of lipids in contrast to the asymmetric lipid positioning in the c₁₁-ring.

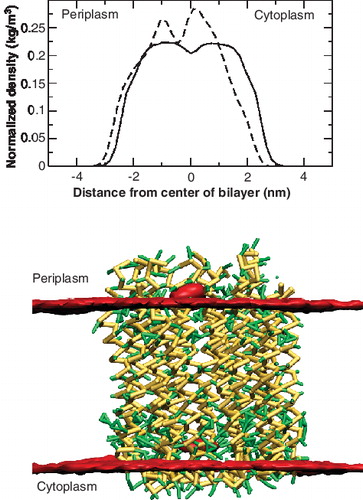
The lipid molecules in the cavity were not aligned with the surrounding bilayer. The density profile of the lipids within the central cavity and those outside is shown in Figure 6 (Top). The density profile is normalized to the total lipid density in the two groups. The bottom panel shows the time-averaged density of the phosphate beads of the bilayer. It is seen that the central lipids tend to be be aligned higher than the rest of the lipid bilayer and protrude towards the periplasmic side. The results agree with those obtained for the I. tartaricus ring [42] where large protrusions and cavities were observed in AFM images. However, the protrusions observed in the 10-mer ring are much less pronounced ranging between 0.2–0.6 nm. The difference in the hydrophobic stretches of the two species that share a sequence identity of about 30% [39] probably causes the lower protrusions.

Figure 6.  Position of the lipids in the central cavity of the c-subunit ring. Top: Density profiles of the POPE lipids in the central cavity of the c-subunit ring (bold) and those surrounding the protein (dotted). The density was calculated perpendicular to the membrane surface and normalized by the total density of the lipids. Below: Lateral view of the time-averaged density of the phosphate beads (red) of the lipids. This Figure is reproduced in colour in Molecular Membrane Biology online.

Diffusion of the c-subunit in POPE membranes

The lateral movement of the ATP synthase in supported membranes has been shown to be characterized by a unhindered free diffusion (linear regime of mean square displacements) and a slower hindered diffusion (non-linear regime) [36]. The diffusion constant for the free diffusion was determined to be 2.04 × 10⁻⁵ μm²/sec. In the simulations presented here, the diffusion of the c-subunit appeared to be much faster. The diffusion constant of the decameric c-subunit ring was calculated to be 6.4 ± 0.3 μm²/sec. The diffusion constant of the free monomer increased by a factor of 10 to 62.2 ± 1.7 μm²/sec. The two estimates of diffusion (simulations and AFM images) cannot be directly compared as interactions between neighboring rotors are not present in our simulations. Another reason for the discrepancy is that membrane proteins moving in supported lipid membranes exhibit diffusion coefficients orders of magnitude lower than when measured in free standing membranes [36]. The calculated diffusion constants are in the same order of magnitude as reported for rhodopsin in bilayers [43].

Discussion

The coarse-grain simulations of the subunit c of ATP synthase allows a characterization of its dynamics up to a quarter of a millisecond. At these time-scales, the c-subunit shows large structural fluctuations and two different helix-helix interfaces are sampled, both in the monomer and in the full ring. The change in the helix-helix interface is caused by the movement of one helix with respect to the other. Previous models have also proposed such a change in the helix interface [2,59]. However, the model postulated that helix-2 swivels around its own axis leading to a change in the residues of helix-2 interacting with helix-1. In the simulations presented here, we observe a swirling of helix-2 around the axis of helix-1, which results in a change of the residues at the interface of helix-1, but not of helix-2. Swirling of helix-2 takes place at microsecond time scale in the monomer systems in our simulations. We cannot exclude that swivelling of helix-2 around its own axis occurs at longer time scales and is thus not sampled in the simulations. However, experimental data such as crosslinking studies [59], that were used to propose the swivelling data, are also consistent with our simulations and do not allow us to differentiate between the two mechanisms. In the crosslinking study, it was proposed that helix-2 could swivel based on the fact that mutations on different faces of the helix-2 could form decameric structures. In the study, mutating residue 21 and residue 65 to cysteine resulted in multimeric aggregates consistent with the E. coli interface. However, mutating residues 21 and 66 also resulted in multimeric aggregates that could be consistent with the I. tartaricus interface. The counter intuitive results could then only be explained by a proposed swivelling of helix-2. In the simulations presented here, the first scenario is possible as residues 21 and 65 in adjacent subunits are less than 0.8 nm apart in interface-1, allowing a hypothetical disulphide bridge. However, the distance between the backbone beads of residues 21 and 66 varies and the distance decreases to less than 0.8 nm indicating that a disulphide bridge between the residues (if mutated to cysteine) is also possible at certain times. This scenario occurs in the simulations when consecutive helices swirl as well as tilt resulting in a decrease in the distance between residues 21 and 66 in consecutive c-subunits. It is also possible that the multimeric aggregates seen in cross-linking study of the 21-66 mutant are not ‘native-like’ arising from helix swivelling but are due to the large number of possible associated states. Multimeric aggregates of more than ten subunits that are seen in the 21-66 mutant support this scenario.

The swirling movement seen in this study appears to be facilitated by the presence of identical aminoacid residues at consecutive positions. Four residues present in the first interface are also present in the second interface. This presents two consecutive Ala-Met-Ala-Ala surfaces offset by 90°. The proposed helix swirling motion would only be possible in other c-subunits if this motif was present. A bio-informatics analysis reveals that the motif is present in only a few members of the family. Though, the pattern is not conserved in the c-subunit family, it is present in other species such as in the Yersina family, indicating that the dynamics may not be unique to E. coli. The structure of the c subunit of E. coli is incompatible with the crystal structure of I. tartaricus, differing in the helix-helix interface. The helix swivelling motion that was proposed for E. coli has not been reported for I. tartaricus. Though the c subunits from the two species share a sequence identity of 30%, the Ala-Met-Ala-Ala consecutive residues motif is not conserved and a similar helical movement is not likely. As expected, preliminary results from our group indicate that no swirling motion is seen in the c-subunit of I. tartaricus at time scales similar to that of E. coli. Investigation of the new model-rotation of helix-1 around around helix-2 and its differences to the existing model of rotation of helix-1 around its own axis merits further attention.

It has also been proposed that swivelling of helix-2 is necessary to expose the functionally- important Asp-61 residue to subunit a [2]. In the model based on steered molecular dynamics simulation studies, a two-step process involving consecutive helix swivelling was proposed that allowed Asp-61 to rotate from position-1 to position-2 in Figure 7. The movement of helix-2, described in this work, has a similar effect in changing the position of Asp-61 (see Figure 7). The exposed surface area of Asp-61 of one monomer increases on swirling only if it precedes a monomer in interface-1. Swirling of a monomer, as described by our model, could thereby increase the accessibility of Asp-61 to subunit a allowing its deprotonation/protonation cycle. Note that Asp-61 is deprotonated in our study and does not point outwards, in contrast to the orientation proposed in an NMR study at high pH [46]. We also carried out control simulations with a protonated Asp-61 and the same change of interface over time is seen. The change of interface over time is shown in Supplementary material (online version only). Thus, whether Asp-61 is protonated or deprotonated does not affect the swirling behavior of the two helices and the swirling seen is independent of the protonation state of Asp-61. Swirling might also be promoted by subunit a, such that the time constants of the isolated ring may not correspond to half times of the c-subunit rotation and proton transport in the entire complex. However, the mechanistic importance of this motion to the functionally-important rotation of the c-subunit is not clear.

Figure 7.  Comparison of the proposed models for rotation of helix-2 (blue) in the c-subunit with respect to helix-1 (red). The view is a top view looking up from the cytoplasmic side of the membrane. The important residues, Ala-20, Ala-21 and Asp-61 are depicted. Top: Rotation of helix-2 around its own axis as proposed by Ref. [2,59]. In this model the helix-2 rotates around its own axis to vary between the two structures depicted. This model predicts a change in the residues at the interface in helix-2. Bottom: Rotation of helix-2 around the axis of helix-1 (red) as seen in the current simulations. In this model, helix-2 rotates around the axis of helix-1 to change the interface of helix-1. This Figure is reproduced in colour in Molecular Membrane Biology online.

A closer look at interface-2 reveals that the residues Leu-31 and Gly-23 do not lie at or close to the interface of the monomer, but are exposed towards the lipid environment. The two residues have been shown to be defective in the assembly of the F_o rotor [23]. Based on the E. coli structure it was proposed that the role of Leu-31 was only indirect and its mutation disrupts the structure of the monomer and does not allow it to assemble [27]. However, helix swirling as proposed by the simulations presented here, rotates the residues to positions where they can be directly involved in subunit associations. Thus, their role in the disruption of the assembly can be more direct than proposed earlier. A closer look at the mutants is required to understand these effects further.

Conclusions

In this paper, we show that coarse-grain models can be used to accurately mimic the behavior of the c-subunit of ATP synthase observed with more detailed simulations. The coarse-grain representation allowed us to sample the dynamics of the system up to hundred of microseconds. On this scale, we observe a helix rotation in the c-subunit monomer which results in a change of the helix-helix interface. The rotation persists in the ring but is considerably slower. The E. coli c ring is proposed here to be filled with six lipid molecules, protruding towards the periplasmic side. The characterization of the monomer and ring states of the c-subunit presented in this work sheds light into its structural fluidity and possible functional mechanism.

Acknowledgments

The research was been supported by funding from The Netherlands Research Organization (NWO). Calculations were performed in part at the Dutch national supercomputing facilities (SARA) through a NCF computer grant. We thank A. Aksimentiev for providing us access to the atomistic simulations and A.J.M. Driessen for helpful discussions.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.