Super resolution in robotic-assisted minimally invasive surgery

Abstract

In minimally invasive surgery, a small field of view is often required to achieve a large magnification factor during micro-scale tasks such as coronary anastomosis. However, constantly changing the orientation and focal length of the laparoscope camera is cumbersome, and can impose extra visual and cognitive load on the operating surgeon in terms of realigning the visual pathways and anatomical landmarks. The purpose of this paper is to investigate the use of fixational movements in robotic-assisted minimally invasive surgery, such that the perceived resolution of the foveal field of view is greater than the intrinsic resolution of the laparoscope camera. The proposed technique is based on super resolution imaging using projection onto convex sets for monochrome images, and a maximum a posteriori method with a novel YIQ space-based prior for color images. Validation with both phantom and in vivo data from totally endoscopic coronary artery bypass surgery is provided.

• Super resolution
• minimally invasive surgery
• robotic-assisted surgery
• endoscopy

Introduction

The use of computer-assisted technology in surgical applications has increased dramatically in recent years, contributing to a range of new methods for training, education and diagnosis. In surgery, advances in medical image computing have enabled detailed preoperative planning and intraoperative surgical guidance. One of the most promising advances in surgical technology in recent years has been the introduction of robotic-assisted Minimally Invasive Surgery (MIS) [1]. This is increasingly being used to perform procedures that are otherwise prohibited by the confines of the operating environment. The technique offers a unique opportunity for deploying sophisticated surgical tools that can greatly enhance the manual dexterities of the operating surgeon [2], [3]. The future of robotic surgery lies in the intelligent use of preoperative data for more complex procedures such as beating-heart surgery, where there is large-scale tissue deformation.

Whilst the benefits of MIS with regard to patient recovery and surgical outcome are well established, its deployment is associated with complexity of instrument controls, restricted vision and mobility, difficult hand-eye coordination, and the lack of tactile perception, which together require a high degree of operator dexterity [4]. For robotic-assisted MIS, dexterity is enhanced with microprocessor-controlled mechanical wrists, which allow motion scaling to reduce gross hand movements and enable performance of micro-scale tasks that are otherwise not possible. So far, however, there has been only limited progress towards resolving the issue of restricted vision. This is largely due to the restriction on the number of trocar ports used during MIS and the small field of view (FOV) required to achieve a large magnification factor for performing micro-scale tasks such as coronary anastomosis. The restricted vision significantly affects the visual-spatial orientation of the surgeon and his awareness of peripheral sites. During MIS, constantly changing the orientation and focal length of the laparoscope camera is cumbersome. This can impose extra visual and cognitive load on the operating surgeon in terms of realigning the visual pathways and anatomical landmarks. In certain cases, this can also contribute to surgical errors, as view rotation is known to affect 3D orientation and thus surgical performance. In MIS, the limited FOV has also made intraoperative surgical guidance difficult due to the paucity of unique surface features for aligning pre- or intraoperative 3D image data.

Alteration of an angle of vision during laparosopic surgery was shown by Ames et al. [5] to lead to deterioration of performance in novice surgeons. The need to change the position of the laparoscopic camera can be avoided by the use of wide-angle endoscopes which cover a large FOV. Cao et al. [6] showed that the use of a wide-FOV monitor does improve performance in terms of surgical maneuverability. They found that the wide-FOV monitor provided additional information to the participant, allowing more efficient performance at high magnifications without the need for zooming. Using super resolution, the additional trocar port insertion needed for a supplemental wide-FOV endoscope [7], [8] can be avoided.

A recent study has demonstrated the benefits of having simultaneous close-up and wide-angle views during MIS [9]. Visual control in the da Vinci surgical systems was improved by adding a large, panoramic FOV visualization of the surgical field. In the study, a stereo endoscope was upgraded with a third optical channel, providing additional 2D wide-angle visualization which could be activated during surgery. Its application to totally endoscopic coronary artery bypass grafting resulted in marked improvement in the surgical work-flow. In this regard, super resolution can be used to simultaneously provide both a large FOV and a large magnification view without the need for the endoscope upgrade.

Recently, gaze-contingent robotic control has attracted significant research interest due to its unique capability in coupling human visual perception with machine vision [10], [11]. The research is based on the fact that, in terms of visual acuity, human eyes do not have a uniform visual response; in fact, the best visual acuity is only within a visual angle of 1-2 degrees. This is called foveal vision, and to see those areas that we do not direct our eyes towards when observing a scene we must rely on a cruder representation of the objects offered by non-foveal vision, the visual acuity of which drops off dramatically away from the center of focus. The limited extent of the fovea demands that the eyes be highly mobile and able to sweep across a large visual angle. As a result, the motion of the eyes is extremely varied in both the amplitude and frequency spectrum. During periods of visual fixation, small eye movements continuously move the projection of the image on the retina [12]. These fixational eye movements include small saccades, slow drifts, and physiological nystagmus. Existing research has shown that micro-motions, including both micro-saccades of the eyes [13] and subpixel (sub-sampling) movements of the visual scene [14], can enhance visual resolution, although the mechanisms of the human visual system are unknown.

The purpose of this paper is to investigate the use of fixational eye movements in robotic-assisted MIS, such that the perceived resolution of the foveal FOV is greater than the intrinsic resolution of the laparoscope camera. In practice, this permits the use of a relatively large FOV for microsurgical tasks, such that the aforementioned drawbacks associated with the existing MIS setup can be avoided. With the proposed method, the position of the surgeon's gaze can be located by using eye tracking. Super resolution can then be used to provide a high-resolution image to the foveal FOV. The proposed technique for monochrome images is based on super resolution imaging using projection onto convex sets (POCS) [15], [16]. Extension to color images employs the maximum a posteriori (MAP) super resolution method [17] with a novel YIQ prior. The YIQ model defines a color space in terms of one luminance (Y) and two chrominance components (I and Q). Validation with both phantom and in vivo data from Totally Endoscopic Coronary Artery Bypass (TECAB) surgery [18] is provided.

Methods

Super resolution is a method for deriving a high-resolution image from a set of low-resolution images that have sub-pixel shifts [14], [19], [20]. The additional information required to calculate the high-resolution image is provided by different “views” given by sub-pixel shifts of low-resolution images. It therefore provides a way of pushing the image resolution beyond the intrinsic limitation of the image sensors.

If one considers high-resolution (HR) image x to be the true representation of the scene, then a low-resolution (LR) image y_i is equal towhere D is a down-sampling operator, M is a warp operator which accounts for translation, rotation and other transformations, H incorporates the point spread function (PSF) of the sensor such as motion blur, and v_i describes the additive noise. The recovery of the HR image x from a set of sub-pixel shifted LR images y_i is the goal of all super resolution algorithms. Existing approaches to the problem include non-uniform interpolation (which consists of sub-pixel LR image registration, interpolation to the HR grid and image restoration) [21], projection onto convex sets (POCS) [15], [16], constrained least squares (CLS) [22], and MAP [17], [23], [24].

The number of non-redundant LR images K needed to achieve a super resolution ratio of L/M is equal towhere L × L and M × M denote the sizes of HR and LR images, respectively. In the underdetermined super resolution cases where K < [L/M]², a regularization term is needed for efficient interpolation of missing data. In an overdetermined case where K > [L/M]², additional information can lead to better noise reduction. For real-time applications where fast convergence is required, it is desirable to choose the number of LR images K to be larger than [L/M]².

Projection onto convex sets

The super resolution reconstruction algorithm used in this work for monochrome images is based on the method of projection onto convex sets [15], [16]. The POCS method is an iterative method which incorporates prior knowledge by restricting the solution to the intersection of closed convex sets. In each iteration, a solution xⁿ⁺¹ is derived such thatwhere P_i are projection operators which project the arbitrary solution xⁿ onto m closed convex sets. Each convex set represents a constraint on the solution such as amplitude, energy, or a reference-image constraint [16]. In other words, the projection operators impose prior knowledge about the HR image on the solution.

Tekalp et al. [15] introduced the following closed convex set constraint for each pixel of each low-resolution frame y_i:where δ₀ defines a bound that represents the statistical confidence in observed LR frames and is usually estimated from the noise present in the LR images. The in a sense represents the difference between the HR image x convolved with a PSF and the i^th LR image y_i:where h_i is a PSF of the sensor for the i^th frame, given by the ratio of the area where LR pixel (m, n) y_i;_m,_n and HR pixel (k, l) x_k,_l overlap divided by the total area of the LR pixel. The projection of an HR image x onto convex set C_i defined in Equation (4) is given by [15]:In this study, the reconstruction of the HR images involves the use of the projection operator presented in Equation (6) together with amplitude and energy constraints. Amplitude constraintrestricts the image intensities to be within the lower and upper bounds, α and β respectively. Similarly, the energy constraint imposes the maximum permissible energy on the reconstructed image.

In practice, parameter δ₀ can be estimated from the noise in low-resolution images automatically. The amplitude constraint bounds are usually set to be the minimum and maximum values of the intensities in the original image and do not require tuning from the user.

Maximum a posteriori super resolution algorithm

For color super resolution reconstruction, a regularization approach based on Bayesian estimation may also be used. As an example, MAP [17], [23], [24] is used to estimate an unobserved quantity on the basis of observed data. The MAP estimate of the HR image is given bywhere Pr(x|y_i) is the likelihood function describing “the likelihood” of the HR image x given the LR observed images y_i. By applying Bayes’ rule this becomesThis is tantamount to minimizing the negative log of the numerator since the denominator is independent of x:The conditional density in the first term, which represents the data fidelity, is equal towhere W_i incorporates down-sampling, warp and blur operators for each of the K LR images, σ is the error variance, and N is the size of the LR images. For the prior term Pr(x) in Equation (10), it is common to choose a Gaussian [25] or Huber-Markov Random Field (MRF) prior [26].

YIQ color super resolution

The super resolution of color images is often performed by using the super resolution on the luminosity channel, then adding the interpolated color channels. In order to use the full available information to improve the resolution of color images, it is necessary to deal with separate color channels. Recently, super resolution has been combined with demosaicing, where an additional term that accounts for dependencies between the color channels has been used [27].

The YIQ model defines a color space in terms of one luminance (Y) and two chrominance components (I and Q). YIQ color is the closest model to the color perception of the human eyes and has been used to derive the following MAP log-likelihood function:for each of the Y, I and Q channels. The coefficients of the coefficient vector d_c for a clique c are chosen to impose smoothness on the HR images, so often first- or second-order derivative discrete approximations are used as a measure of smoothness. The “temperature” of the Gibbs density function [28] used to model the HR image is given by parameter λ, which represents a smoothing parameter to provide a tradeoff between the smoothness of the image estimate and data fidelity. Cross validation [29] can be used to estimate the value λ for a given set of images automatically.

The solution to Equation (12) represents the super resolution reconstructed image, which can be found by an optimization algorithm. In this study, the following algorithm based on gradient descent is used, with which the (n + 1)^th iteration of the image is updated according towhere α is the optimization step size. The gradient is calculated separately for each channel. For example, the Y-channel gradient is equal toSimilar expressions can be derived for the I and Q chrominance channels. By combining the three separate super resolved images, true color super resolution can be achieved.

Image registration

For super resolution imaging, accurate image registration is crucial to the subsequent reconstruction result. The precision of the registration has to be accurate to a fraction of a pixel. While there are many methods that address registration to the pixel level, sub-pixel registration is more difficult and requires careful consideration. Phase correlation methods [30] are based on the fact that in the frequency domain two shifted images differ only by a phase shift, and therefore correlation of the Fourier transforms of the images is used to calculate the relative shift between images. While accurate, phase domain methods are not practical for real-time applications due to the large computational load. Spatial domain methods are based on direct manipulation of the image data. Keren et al. [31] developed an iterative motion estimation algorithm based on a Taylor series expansion. A pyramidal scheme is used to increase the precision of image registration for large motion parameters. This method proved to be fast and robust and is used for this work. Block Matching methods [32], which treat small blocks of pixels in the image separately, are useful in situations where non-uniform shifts within the images are present and full-frame registration is not possible.

Experimental setups

To validate the proposed super resolution framework for MIS, a Stäubli RX60 robotic arm was used to control the sub-pixel movement of the camera. The system has six degrees of freedom (DOF) and a repeatability accuracy of ± 0.02 mm at high speed and acceleration. A phantom heart model was created by using thixotropic silicone mold rubber and pre-vulcanized natural rubber latex with rubber mask grease paint to achieve a specular appearance and high visual fidelity. A video sequence was captured using a camera mounted on the described robotic arm. The camera was moved in a zigzag pattern with the total movement spanning, on average, 2-4 pixels. From the video sequence, 40 images were extracted and each image was separately down-sampled to one fourth of the original resolution to ensure that the algorithm remained “blind” to individual frame shifts. To assess the in vivo applicability of the technique, two video sequences from a totally endoscopic coronary artery bypass (TECAB) surgery were used. The natural camera motion during the operation was sufficient to provide a set of non-redundant shifted images, as the shifts between the images enhanced by super resolution only need to differ by sub-pixel motion. There is no need to track the motion of the camera, as image registration methods can provide image shifts with the desired sub-pixel accuracy.

Results

Figure 1 shows one example image of the phantom heart experiment: Figure 1a shows a video snapshot of the “true”, actual scene (original image); Figure 1b is the corresponding LR image obtained by down-sampling; and Figure 1d illustrates the result of the described POCS super resolution algorithm as applied to the set of 40 registered LR images. The insert in each panel shows a magnified view of the FOV indicated by the arrow, demonstrating the high-resolution details that have been recovered by the proposed POCS algorithm.

Figure 1. (a) A video snapshot of the actual scene (original image) of the phantom experiment, and (b) the corresponding LR images obtained by down-sampling. (c) For comparison, the LR image in (b) was re-sampled using cubic interpolation. (d) The resulting image after application of the described POCS super resolution algorithm; the insert demonstrates the high-resolution details recovered by the proposed algorithm.

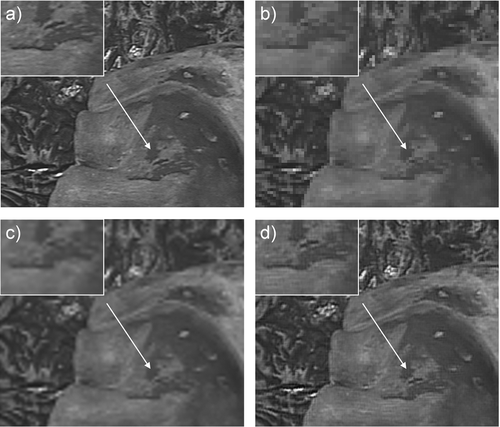
To quantify the level of detail reconstructed in the HR image, an entropy measure [33] that represents the amount of information present in the images is calculated. Larger entropy values in general are indicative of the high-resolution details recovered. For the phantom study, the entropy values of the original, LR, interpolated, and POCS-reconstructed HR images are 6.74, 6.57, 6.56 and 6.72, respectively, which suggests the information recovered by the HR image is close to 99.7%, based on the entropy measure. It should be noted, however, that this is a global statistical measure, and may not represent the actual visual fidelity recovered. Nevertheless, it does provide a quantitative index when combined with visual feature assessment.

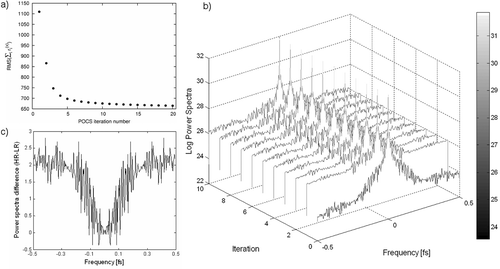
To examine the convergence behavior of the algorithm, Figure 2a illustrates the RMS error in relation to the iteration steps. The algorithm in general has a rapid convergence rate, which makes it suitable for real-time implementations. In Figures 2b and 2c, the power spectra of the LR and HR images are also provided, demonstrating the amount of high-frequency detail recovered.

Figure 2. (a) The convergence of the POCS algorithm as demonstrated by the RMS error defined in Equation (4). (b) The power spectra of the LR image (at the zero position) and HR images for the first 10 iterations (where fs denotes the spatial sampling frequency). (c) Plot showing the difference in power spectra between the LR and HR images for the 10^th iteration.

For in vivo data, Figure 3 illustrates an FOV corresponding to the foveal region of the fixation and the high-resolution details recovered by the POCS algorithm, with the corresponding images before resolution enhancement provided for reference. This figure also indicates the position of the FOV in relation to the operating view. To provide a more accurate assessment of the level of detail recovered, Figure 4 illustrates the intensity profiles as marked in Figure 3 for each of the images presented. The corresponding entropy measures for these images are summarized in Table I.

Figure 3. (a) Original video image frames from a TECAB sequence. (b) The corresponding magnified time frames from the region marked by the white square in (a). (c) HR reconstructions calculated using the described POCS method. White lines in b and c indicate rows for which intensity profiles are shown in Figure 4.

Figure 4. Pixel intensity profiles across image features on both HR (solid lines) and LR (dashed lines) images, showing the improved resolution of the reconstructed image for the time series shown in Figure 3. Pixels used for line profiles are marked by white lines in Figure 3(b and c) .

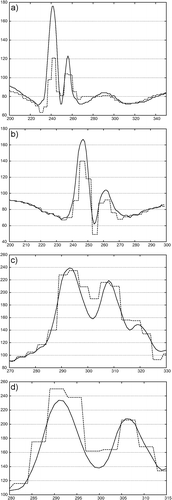
Table I.  Entropy values for the TECAB images shown in Figure 3.

Time series	LR image	HR image	Difference HR–LR
1	6.72	6.83	0.11
2	6.78	6.82	0.04
3	6.79	6.85	0.06
4	6.79	6.84	0.05

The second in vivo experiment, as illustrated in Figure 5, was used to demonstrate the benefits of the proposed color super resolution method. The corresponding results obtained by applying the proposed algorithm are provided in Figure 6. It is evident that the HR image provides enhanced details compared to those of the LR image without suffering from color artefacts. To provide a more quantitative assessment of the image quality achieved, Figure 7 illustrates separate RGB line profiles of the LR and HR images shown in Figure 6.

Figure 5. (a) Representative image frames from the 2^nd in vivo experiment demonstrating the benefits of the proposed color super resolution method. (b) The relative shifts between the image frames. (c) One of the video frames with the region of interest marked; the super resolution details of this region are shown in Figure 6. [Color version available online.]

Figure 6. a) The LR image from the marked region in Figure 5c. b) The corresponding SR image reconstructed from the MAP-YIQ method. [Color version available online.]

Figure 7. Color profiles of LR and HR images along the white lines shown in Figure 6. [Color version available online.]

Discussion and conclusions

In this paper, we have demonstrated the use of super resolution for robotic-assisted MIS. The basic motivation of the technique is to investigate the use of fixational movements in robotic-assisted MIS such that the perceived resolution of the foveal FOV is greater than the intrinsic resolution of the laparoscope camera. This will allow the use of a relatively large FOV for microsurgical tasks such that super resolution is applied to fixations in response to real-time eye tracking. Experiments with both phantom data in a controlled environment and video sequences from a TECAB procedure have been used. The results derived by using both POCS and MAP–YIQ reconstructions demonstrate the potential value of the proposed technique in improving the apparent spatial resolution of the images. It is expected that, in combination with eye tracking, the described method can provide the operator with gaze-contingent super resolution foveal vision, thus minimizing the need for manual adjustment of the laparoscope camera during surgery. Specifically, reconstructed images can be used to replace the images available to the operating surgeon or, alternatively, they can be displayed on a separate screen to simultaneously show wide-FOV and zoomed-in views of the observed scene.