Combining a breathing model and tumor-specific rigidity constraints for registration of CT-PET thoracic data

Abstract

Diagnosis and therapy planning in oncology applications often rely on the joint exploitation of two complementary imaging modalities, namely Computerized Tomography (CT) and Positron Emission Tomography (PET). While recent technical advances in combined CT/PET scanners enable 3D CT and PET data of the thoracic region to be obtained with the patient in the same global position, current image data registration methods do not account for breathing-induced anatomical changes in the thoracic region, and this remains an important limitation. This paper deals with the 3D registration of CT thoracic image volumes acquired at two different instants in the breathing cycle and PET volumes of thoracic regions. To guarantee physiologically plausible deformations, we present a novel method for incorporating a breathing model in a non-linear registration procedure. The approach is based on simulating intermediate lung shapes between the two 3D lung surfaces segmented on the CT volumes and finding the one most resembling the lung surface segmented on the PET data. To compare lung surfaces, a shape registration method is used, aligning anatomical landmark points that are automatically selected on the basis of local surface curvature. PET image data are then deformed to match one of the CT data sets based on the deformation field provided by surface matching and surface deformation across the breathing cycle. For pathological cases with lung tumors, specific rigidity constraints in the deformation process are included to preserve the shape of the tumor while guaranteeing a continuous deformation.

• CT
• PET
• volume registration
• thorax
• lung
• breathing model
• landmark point selection
• rigidity constraints

Introduction

Lung radiotherapy has been shown to be effective for the treatment of lung cancer. This technique requires a precise localization of the pathology and a good knowledge of its spatial extent in order to monitor and control the dose delivered inside the body to both pathological and healthy tissues. Radiotherapy planning is usually based on two types of complementary image data: Positron Emission Tomography (PET) images, which provide good sensitivity in tumor detection and serve as a reference for computing relevant indices such as SUV (Standardized Uptake Value), but do not provide a precise localization of the pathology; and Computerized Tomography (CT) images, which provide precise information on the size and shape of the lesion and surrounding anatomical structures, but only reduced information concerning malignancy. Joint exploitation of these two imaging modalities has a significant impact on improving medical decision-making for diagnosis and therapy [1–3], while requiring registration of the image data. The registration is important for radiotherapy, in addition to segmentation, given that neither of the two modalities provide all the necessary information. Finally, to visualize the overall pathology in the lungs, it is necessary to register the whole volume and not just regions of interest such as tumor or heart regions. In this paper, we investigate the case of thoracic images depicting lung tumors. Examples of CT and PET images are shown in Figure 1.

Figure 1. CT images (coronal views) corresponding to two different instants in the breathing cycle, end-expiration (a) and end-inspiration (b), and a PET image (c) of the same patient (patient A in our tests). [Color version available online.]

Combined CT/PET scanners, which provide rigidly registered images, have significantly reduced the problem of registering these two modalities [4]. However, even with combined scanners, non-linear registration remains necessary to compensate for cardiac and respiratory motion [5]. The most popular approaches are elastic registration [6], fluid registration [7] and the demons algorithm [8]. More complete surveys of image registration can be found in references [9], [10] and [11].

In the particular case of lungs and lung tumors, the difficulty of the problem is increased as a result of the patient's breathing and the induced displacement of the tumor, which does not undergo the same type of deformation as the normal lung tissues. For example, the tumor is not dilated during the inspiration phase. As a first approximation, its movement can be considered as rigid. Unfortunately, most of the existing non-linear registration methods do not take into account any knowledge of the physiology of the human body or of the tumors. Some methods have been proposed to introduce local constraints based on FFD (Free Form Deformation) [12], variational and probabilistic approaches [13], landmark points [14], [15] and local rigidity constraints [16]. With the exception of the last approach, none of these methods really take into account the shape of the tumor. Consequently, all of these non-linear methods provide an accurate estimation of the deformation of the surface of the lungs, but rigid structures, such as tumors, are artificially deformed at the same time and the valuable information in the area of the pathology may be lost. This limitation is illustrated in Figure 2: the tumor suffers non-realistic deformations when a global non-linear registration is applied.

Figure 2. Non-linear registration without tumor-based constraints. (a) A slice of the original CT image. (b) The corresponding slice in the PET image. (c) The registered PET. The absence of constraints on the tumor deformation leads to undesired and irrelevant deformations of the pathology. In (a), the cursor is positioned on the tumor localization in the CT data, and in (b) and (c) the cursor points to the same coordinates. This example shows an erroneous positioning of the tumor and illustrates the importance of tumor segmentation and the use of tumor-specific constraints during the registration in (c). [Color version available online.]

In this paper, we propose to overcome these limitations by developing a non-linear registration method with two key features: a breathing model is used to ensure physiologically plausible deformations during the registration; and the specific deformations of the tumors are taken into account while preserving the continuity of the deformations around them. In the context of radiotherapy treatment planning, precision requirements for registration and delineation of lung and tumor borders are somewhat alleviated by the use of a security margin around the tumor. As a consequence, millimetric precision is not required, and it is possible to work on the PET data without having to cope specifically with its limited resolution and induced partial volume effects. A precision of 1 or 2 centimeters is typically considered sufficient for such applications.

The proposed method involves first a series of surface registrations and then image volume registration. Its main components can be summarized as follows:

1. A physiologically driven breathing model is introduced into a 3D non-linear surface registration process. This model computes realistic deformations of the lung surface. Whereas several breathing models have been developed for medical visualization, for correcting artifacts in images, or for estimating lung motion for radiotherapy applications, few papers exploit such models in a registration process.

2. Physiology is further taken into account with a landmark-based surface registration, by selecting anatomical points of interest and forcing homologous points to match.

3. Volume registration is based on the displacement field identified during surface registration, combined with rigidity constraints that help preserve the size and shape of the tumors, as an extension of the method proposed by Little et al. [16]. Constraints on the heart are also introduced.

This paper is an extended version of our previous work [17]. Moreover, new steps are proposed, in particular the introduction of rigidity constraints on the heart and a quantitative evaluation of the proposed method. Figure 3 shows the complete computational workflow. After describing previous research exploiting breathing models for radiotherapy applications in the next section, each component of the proposed registration method is detailed in the succeeding sections, namely the segmentation, the breathing model and its adaptation to a specific patient, and the non-linear registration based on landmark points and rigidity constraints. Finally, clinical evaluation and a discussion are presented.

Figure 3. Registration of CT and PET volumes using a breathing model. Segmentations are performed on the volumes, whereas simulation of lung shapes is based on surface meshes. Consequently, the first two steps of the registration process are performed on meshes, while the final step, concerning PET deformations, is computed on the volumes: We obtain a dense registration of the PET volume to the original CT volume.

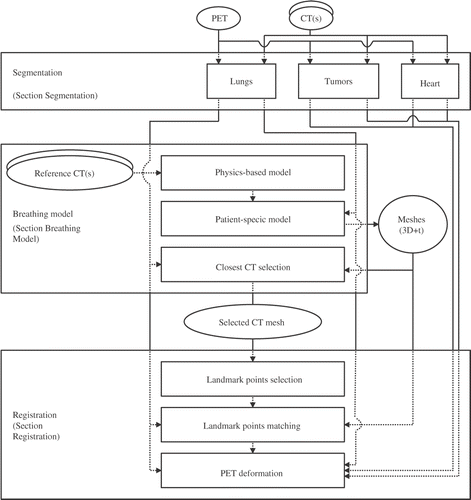
Overview of breathing models and registration

Currently, respiration-gated radiotherapies are being developed to improve radiation dose delivery to lung and abdominal tumors [18]. Movements induced by breathing can be taken into account at two different levels: during the reconstruction of the 3D volumes and/or during the treatment. In the case of reconstruction of volumes, the methods depend on the equipment [19], [20]: the respiration signal must be acquired and synchronized with the acquisitions.

In order to take into account breathing during the treatment, three types of techniques have been proposed so far: active techniques [21], passive or empirical techniques [22–26], and model-based techniques [27]. We are particularly concerned with the model-based techniques because the deformations of the surfaces of the lungs can be precisely computed with these methods and, in contrast to passive methods, specific equipment is not necessary. Two main types of model can be used: geometrical or physical.

For geometrical models, the most popular technique is based on Non-Uniform Rational B-Spline (NURBS) surfaces that are bidirectional parametric representations of an object. NURBS surfaces have been used to correct for respiratory artifacts in cardiac SPECT images [28]. A multi-resolution registration approach for 4D Magnetic Resonance Imaging (MRI) was proposed [29] for evaluating amplitudes of movement caused by respiration, and a 4D phantom and an original CT image were also recently used to generate a 4D CT and compute registration [30].

Physically based models describe the important role of airflow inside the lungs, which requires acquisition of a respiration signal. Moreover, these models can be based on Active Breathing Coordinator (ABC), which allows clinicians to pause the patient's breathing at a precise lung volume. Some methods are also based on volume preservation [31–35].

Only a few studies have really employed a breathing model in a registration process. Segmented MRI data was used to simulate PET volumes at different instants in the breathing cycle [36]. These estimated PET volumes were used to evaluate different PET/MRI registration processes. Other researchers [29], [37] used pre-registered MRI to estimate a breathing model, while the use of CT registration to assess the reproducibility of breath-holding with ABC was recently presented [27]. In another method, the respiratory motion is estimated with a variational approach that combines registration and segmentation of CT images of the liver [38]. Overall, previous studies have used and estimated breathing models for visualization, simulation, or medical investigations, but none has introduced the use of such models for multi-modal registration in radiotherapy applications. From a modeling and simulation point of view, physically based models are better suited for simulating lung dynamics and are easy to adapt to individual patients, without the need for external physical controls.

Segmentation

As previously shown in numerous papers, including reports from our own group [39], the registration of multi-modal images in strongly deformable regions such as the thorax benefits greatly from a control of the transformations applied to the different organs. This control can rely on a previous segmentation of homologous structures that are visible in both images. In the thorax, the problem is exemplified by the fact that the organs may undergo different types of deformation during breathing and patient movements. Therefore, the proposed method relies on the segmentation of different anatomical structures:

• Surface of the lungs. The generation of meshes at different instants in the breathing cycle is based on instances of the lung surface geometry.

• Tumors inside the lungs. To take into account the specific deformations of the tumors, we need to locate and segment the pathologies.

• Heart. In this work, we do not deal with the difficult problem of heart registration. However, the lung deformations must not affect this organ and, for this reason and as a first approximation, we consider the heart as a rigid structure in our method.

The segmentation of the lungs in CT images has been detailed in our previous work [40]. It relies on a classification based on grey levels. The best class is chosen according to its adequation to general anatomical knowledge concerning typical volume values for the lungs. Some refinement steps are then performed, based on mathematical morphology operations and a deformable model, with a data fidelity term based on gradient vector flow and a classical regularization term based on curvature. Two types of images can be acquired in PET: an emission image (in which the tumor can be seen, but the surface of the lungs is not well visualized) and a transmission image (in which the tumor cannot be seen as well as in the emission image, but the surface of the lungs is easier to detect). In most of the acquisitions, only the emission image was stored, being the most significant one for diagnosis. Consequently, if possible, the segmentation is performed on the transmission image, using a similar approach as with CT. If the transmission image is not available and the PET image comes from a combined CT/PET machine, then the segmentation of the lungs in CT is used to provide a rough localization. Otherwise, the segmentation of the lungs in PET is performed directly on the emission images (examples are provided in Figure 4) for CT segmentation.

Figure 4. (a) Coronal view in an original CT image. (b) The segmented lungs in this CT image.

The segmentation of the tumor is semi-automatic [40] (examples are shown in Figure 5). The user selects a seed point inside the tumor, then a region-growing approach is used to segment the tumor in the PET and CT images. It should be noted that an ultra-precise delineation of the tumor is not required. In particular, we do not have to deal with the partial volume effect. The segmentation is only used to impose a specific transformation in the region of the tumor, which is different from that of the lungs, and the continuity constraints imposed on the deformation field ensure that the transformation evolves smoothly and slowly as the distance to the tumor increases, thus guaranteeing that the final registration is robust to the segmentation. The segmentation method for the lungs and tumors has been successfully tested on more than 20 cases, featuring various tumor positions and sizes.

Figure 5. Results of automatic heart segmentation (green contour) for two cases where a tumor (red contour) is present in the right (a, b) and left (c, d) lungs. [Color version available online.]

The segmentation of the heart is a challenging and important problem. Although the majority of existing methods concern the segmentation of the ventricles, there is a real need to be able to segment the heart as a whole. An original method [41] has been proposed based on anatomical knowledge of the heart, in particular with regard to its position between the lungs. The “between” relation can be efficiently modeled mathematically in the fuzzy set framework, thus dealing with the intrinsic imprecision of this spatial relation [42]. Computing this relation for the two segmented lungs leads to a fuzzy region of interest for the heart that is incorporated in the energy functional of a deformable model. This method has been applied successfully on more than 10 non-contrast CT images, yielding good accuracy with respect to manual segmentations (a sensitivity of 0.84 and an average distance between the two segmentation results of 6 mm), and good robustness with respect to the parameters of the method. This evaluation has been detailed in our previous work [41]. Some examples of heart segmentation are illustrated in Figure 5. In PET images, the heart is manually segmented at this stage of development.

Breathing model

Physics-based dynamic 3D surface lung model

Here we briefly describe the breathing model [43], [32] used in this work. The two major components involved in the modeling are the parametization of PV (Pressure-Volume) data from a human subject, which acts as an ABC (cf. Figure 6), and the estimation of the deformation operator from 4D CT lung data sets.

Figure 6. The physics-based breathing model. (a) depicts the pressure-volume relation, and (b) and (c) are two meshes of the breathing model obtained with the reference 4D CTs. (b) is the end-expiration mesh, and (c) is the end-inspiration mesh. This is the initial breathing model (based on a reference image) before any adaptation to a specific patient. [Color version available online.]

The parametrized PV curve, obtained from a human subject, is used as a driver for simulating the 3D lung shapes at different lung volumes [32]. For the estimation, a subject-specific 3D deformation operator, which represents the elastic properties of the deforming 3D lung surface model, is estimated. The computation takes as input the 3D nodal displacements of the 3D lung surface meshes and the estimated amount of force applied on the nodes of the meshes (which are on the surface of the lungs). Displacements are obtained from 4D CT data of a human subject. The directions and magnitudes of the displacements of the lung surface points are computed for the 4D CT using the volume linearity constraint, i.e., the fact that the expansion of lung tissues is related to the increase in lung volume and the cardiac motion. The amount of applied force on each node, which represents the air flow inside the lungs, is estimated based on a PV curve and on the lungs’ orientation with respect to gravity, which controls the air flow. Given these inputs, a physics-based deformation approach based on Green's function (GF) formulation is estimated to deform the 3D lung surface meshes. Specifically, the GF is defined in terms of a physiological factor, the regional alveolar expandability (elastic properties), and a structural factor, the inter-nodal distance of the 3D surface lung model. To compute the coefficients of these two factors, an iterative approach is employed and, at each step, the force applied on a node is shared with its neighboring nodes, based on local normalization of the alveolar expandability coupled with inter-nodal distance. The process stops when this sharing of the applied force reaches equilibrium. For validation purposes, a 4D CT data set of a normal human subject with four instances of deformation was considered [32]. The simulated lung deformations matched the 4D CT data set with an average distance error of 2 mm.

Computation of a patient-specific breathing model

For each patient, we only have two segmented 3D CT data sets (typically acquired at end-expiration and end-inspiration). Therefore, we first estimate intermediate 3D lung shapes between these two meshes, followed by the displacements of lung surface points. Since only two 3D CT data sets are used, the registration is performed using a volume linearity constraint and a surface smoothness constraint that enables us to account for large surface deformations. Thus, the direction vectors for the surface nodes are given by the mode described in the preceding sub-section and the surface smoothness constraint. The direction vectors of the lung surface displacement are computed as follows: Their initial values are set based on the direction vectors computed for a 4D CT data set. The volume linearity constraint ensures that the expansion of lung tissues is linearly related to the increase in lung volume. To ensure surface smoothness during deformation, the lung surface is divided into two regions, cardiac and non-cardiac. Of particular importance is the registration of the lung surface in the cardiac region, where the deformation is important, given the heart movements. The smoothness constraint for the cardiac region is set to minimize the average of the smoothness operator computed for every surface node, whereas for the lung surface in the non-cardiac region, the supremum of the smoothness operator is minimized. The magnitudes are computed from the given 3D CT lung data sets and their directions of displacement.

For known directions of displacement, the magnitude of the displacement is computed from the two 3D CT lung data sets by projecting rays from the end-expiratory lung surface node along the directions of the displacement (previously computed) to intersect with the end-inspiration lung surface primitives (triangles). With known estimations of the applied force and “subject-specific” displacements, the coefficients of the GF are estimated. The GF operator is then used to compute the 3D lung shapes at different lung volumes. In Figure 7, an example of meshes for one patient is given, showing the volume variation caused by breathing. This estimation allows the intermediate 3D lung surface shapes to be computed in a physically and physiologically accurate manner, which can then be used to register the PET images, as further discussed in the following sections.

Figure 7. Three simulated CTs for one patient (patient A in our tests), representing two intermediate points (a and b) and the end-inspiration (c). The red crosses are on the same 3D points in each volume. [Color version available online.]

Simulated CT selection

To introduce physiological constraints and improve the landmark points matching, we propose to simulate a CT mesh that is as close as possible to the original PET. A possible first approach could be to simulate an average CT volume; however, in that case, we would not have the benefit of the precise generation of CT instants during the breathing cycle, and the breathing deformations could not be introduced. We assume that, even if the PET volume represents an average volume throughout the respiratory cycle, by using a breathing model we can compute a CT volume at a given instant that can be closer to the PET volume than the original CT volumes.

Let us denote the CT simulated meshes M₁, M₂, …, M_N with M₁ and M_N corresponding to the CT in maximum exhalation and maximum inhalation, respectively. By using the breathing model, the transformation φ_i,j between two instants i and j in the breathing cycle can be computed as M_j = φ_i,j (M_i). By applying the continuous breathing model, we then generate simulated CT meshes at different instants (“snapshots”) in the breathing cycle. By comparing each CT mesh with the PET mesh (M_PET - the PET mesh is simply derived from the segmented lung surface in the PET data), we select the “closest” one (i.e., the one with the most similar shape). The mesh that minimizes a measure of similarity C (root mean square distance) is denoted as M_C, given as

Registration

To obtain physiologically realistic transformations, anatomical points of interest (landmark points) are introduced which are selected and then matched on the lung surfaces. Consequently, the quality of the registration results will depend on the quality of the landmark points matching process, which takes anatomical knowledge into account by using the surface meshes estimated with the breathing model.

Landmark point selection

Here we focus on voxel selection, but more complex features can also be detected [44] such as edges or regions. The selection can be manual (as in most methods) [15], semi-automated or automated [45]. Manual selection of landmark points is tedious and time-consuming, motivating Hartkens et al. [14] to suggest semi-automated selection integrating expert knowledge in an automatic process. Automatic selection decreases computational time while preserving high accuracy and allowing anatomical constraints, relying on curvature, for example [45], [46].

In this sub-section, we use the meshes corresponding to the segmented surfaces (see Segmentation section above). We consider that anatomical points of interest correspond to points with local maximal curvature. Gaussian and mean curvatures are both interesting because different anatomical points of interest can be detected: mean curvature can help detect points on costal surfaces, whereas other points of interest can be easily detected on the apex of the lungs by using Gaussian curvature. In the present work, landmark point selection is automatic and is based on curvatures as follows:

1. Compute mean and/or Gaussian curvature(s) for each voxel of the lung surface;

2. Sort voxels in decreasing order of absolute curvature values;

3. Select voxels based on curvature and distance criteria (detailed in the following paragraph);

4. Add voxels with zero curvature in underpopulated areas.

This algorithm is designed to select voxels that provide relevant information. In addition to this, we need to obtain an approximately uniform spatial distribution of landmark points to apply deformations on the entire lung surface. If no landmark point is selected in a large flat area, large interpolation errors might arise after the registration step (cf. the PET deformation sub-section below) (our interpolation allows strong deformations if it is not sufficiently controlled). Thus, in step 3, we consider 𝒱 = {v_i}_{i=0···N𝒮}, the set of voxels in decreasing order of absolute curvature values, where N_𝒮 is the number of voxels of the surface; and 𝒱_ℒ = {v_ℒi}_{i=0···Nℒ}, the set of landmark points, where N_ℒ is the number of landmark points. For each voxel v_i ∈ 𝒱, i = 0···N_𝒮 with non-zero curvature, we add v_i in 𝒱_ℒ, if ∀v_j ∈ 𝒱_ℒ, d_g(v_i, v_j) > T, where d_g is the geodesic distance on the lung surface and T is a threshold to be chosen. The geodesic distance on the surface is computed efficiently using a propagation method, similar to the Chamfer algorithm [47]. With this selection process, some regions (the flattest ones) may contain no landmark point, hence the addition of step 4: For each voxel on the surface v_i ∈ 𝒱 with zero curvature, if there is no landmark point v_j ∈ 𝒱_ℒ with d_g(v_i, v_j) < T, we add v_i in 𝒱_ℒ.

For this landmark point selection process, four variants have been tested:

1. MEA: Mean curvature without step 4;

2. GAU: Gaussian curvature without step 4;

3. MEA-GAU: Using mean and Gaussian curvatures without step 4;

4. MEA-GAU-UNI: Using mean and Gaussian curvatures with step 4.

When mean and Gaussian curvatures are both employed (MEA-GAU and MEA-GAU-UNI), the set 𝒱 merges the set of voxels in decreasing order of mean curvature and the set of voxels in decreasing order of Gaussian curvature by taking a value from each set alternately. These strategies for landmark point selection are compared in Figure 8. Results given by the MEA and GAU methods are different, and it is interesting to combine them (see the results obtained with the MEA-GAU method). The MEA-GAU-UNI method permits some points to be added in locally flat regions. The influence of the choice of the strategy on the respiration results will be further considered in the Results and discussion sub-section.

Figure 8. Selection of landmark points on the same axial view of the lung (patient B in our tests). In each image, two regions of interest are identified with two rectangles. In the large rectangle, there is no landmark point with the GAU method (b), whereas there are four landmark points with the MEA method (a). In the fusion MEA-GAU method (c), these landmark points are selected. In the small rectangle, no landmark point is selected with the mean and/or the Gaussian curvatures (a-c). However, a landmark point is added in this area with the MEA-GAU-UNI method (d). This example illustrates the selected landmark points on one slice, but the selection has been computed on the volume. For this reason, no voxel has been selected in the left flat region, i.e., a voxel has been selected in a close slice.

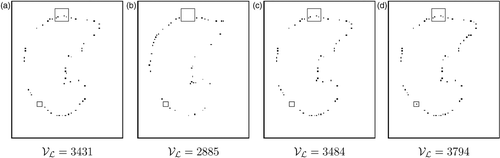
Landmark points matching

We now discuss the steps taken in the computation of patient-specific breathing models, which will be used for the PET-CT registration. The landmark points are selected on the original CT lung surface mesh M_N (cf. the preceding sub-section), and we compute the matching of the landmark points with the original PET mesh M_PET (all the nodes of the PET mesh are tested).

A direct matching, denoted as f ^Rd, can be computed (dashed line in Figure 9):where is the result of matching M_PET directly to M_N (note that this could be done with another instant in the breathing cycle M_i). Most of the matching methods give good results when the two volumes are quite similar or quite near to one other. However, when the original CT lungs volume is very different from the original PET lungs volume, the matching may be inaccurate. To alleviate this problem, we propose to exploit the breathing model and introduce a breathing-based matching based on the Iterative Closest Point (ICP) [48].

Figure 9. Matching framework of the PET (M_PET) and the original CT (M_N): The M_C mesh is the closest to the M_PET mesh. We can match landmark points between M_PET and M_N by following one of the two paths. The proposed method corresponds to the bold line.

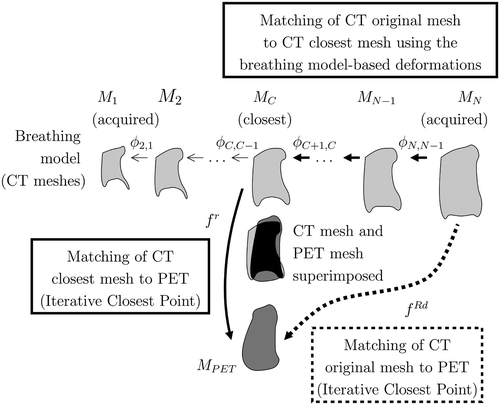
The transformation caused by the breathing is used to match the landmark points (continuous line in Figure 9) incorporating the transformation between M_N and M_C (the CT mesh closest to M_PET) given by the breathing model:We apply Φ_N,C to M_N to obtain the corresponding landmark points on M_C, where M_C = Φ_N,C (M_N). Then we compute the matching f ^r of the landmark points in M_C with the M_PET aswhere denotes the corresponding nodes on the M_PET. As M_C is the closest mesh to M_PET, the inaccuracy of ICP (used in this stage), introduced by important distances between the objects, is minimized. Therefore, the final matching is given bywhere denotes the corresponding nodes on the PET mesh using the breathing model.

PET deformation

The final step in the multi-modality registration process consists of computing the deformation of the whole PET image volume, and not only the segmented lung surface. This task is based on the previous results from landmark point correspondences and lung segmentation. We take into account the presence of tumors in the registration process by introducing rigidity constraints and by enforcing continuous deformations [49]. Tumors are compact pathological tissues, and we can assume that their deformations are different from the alveolar expandability. As a first approximation, rigid deformation of the tumors has been validated by physicians.

Deformations for the whole PET image volume are estimated based on correspondences between anatomical landmark points (cf. the two preceding sub-sections on selection and matching of landmark points): at each voxel location, the displacement is computed as an interpolation of the landmark correspondence displacement field. The interpolation takes into account the distance between the voxel and each landmark point, while guaranteeing a continuous deformation field and constraining rigid structures. More precisely, the vector of displacements f(t) of the voxel t is given by

where t_j are the N_ℒ landmark points in the source image that we want to transform to new sites u_j (the homologous landmark points) in the target image. This is imposed by the constraints

The first term of Equation 6 represents the linear transformation and the second term represents the non-linear transformation of every point t in the source image.

The linear term. When N₀ rigid objects (O₁, O₂, …, O_N0) are present, the linear term is a weighted sum of each object's linear transformation. The weights w_i(t) are inversely proportional to the distance from t to each structure and, for any point t,where L_i, i = 1, …, N₀ are the linear transformations of the rigid objects (the tumors and the heart). The weights w_i(t) depend on a measure of distance d(t, O_i) from the point t to the object O_i:where and μ = 1.5 for the work illustrated here. The smoothness of the interpolation is controlled by the choice of this parameter. A value of μ > 1 ensures that the first derivative is continuous.

The non-linear term. The non-linear transformation is, for a point t, the sum of N_ℒ terms, one for each landmark point. Each term is the product of the coefficients of a matrix B (that will be computed in order to satisfy the constraints on the landmark points) with a function σ(t, t_j) that introduces rigidity constraints corresponding to the rigid structures, which do not have to follow the transformation associated to the lung surface. This is the main contribution of the registration method. This function σ(t, t_j) is defined aswhere d(t, O₀) is the distance from point t to the union of rigid objects O₀ = O₁ ∪ O₂ ∪···∪ O_N0. It is equal to zero for t ∈ O₀ (inside any of the rigid structures) and takes small values when t is near one of the structures. This measure of the distance is continuous and weights the |t − t_j| function [50]. Note that this formalism could be made more general by replacing d(t, O₀) with any function of the distance to O₀ that characterizes more accurately the behavior of the surrounding regions. We have used a linear (normalized) distance function as a first approach.

Finally, with the constraints given by Equation 7, we can calculate the coefficients b_j of the non-linear term by expressing Equation 6 for t = t_i. The transformation can then be defined in a matricial way aswhere U is the matrix of the landmark points u_i in the target image (the constraints), Σ_ij = σ(t_i, t_j) (given by Equation 10), B is the matrix of the coefficients of the non-linear term b_i, and L represents the application of the linear transformations to the landmark points in the source image, t_i. From Equation 11, the matrix B is obtained asOnce the coefficients b_i of B are found, we can calculate the general interpolation solution for every point, as shown in Equation 6.

The importance of the non-linear deformation is controlled by the distance to the rigid objects in the following manner (cf. Figure 10):

• d(t, O₀) makes σ(t, t_j) tend towards zero when the point for which we are calculating the transformation is close to one of the rigid objects;

• d(t_j, O₀) makes σ(t, t_j) tend towards zero when the landmark point t_j is near one of the rigid objects. This condition means that the landmark points close to the rigid structures hardly contribute to the non-linear transformation computation;

• When both t and t_j are far from the rigid objects, then σ(t, t_j) ≃ |t − t_j|.

Figure 10. Illustration of the influence of the distance to the rigid objects (black ellipses) in the non-linear deformation. Two different positions of a point t (one close to and one far from the rigid objects) are shown, and two points of interest are represented by t_j and t_k. When a point of interest is close to a rigid object, like t_k, it has little influence in the non-linear term in Equation 6 (cf. Equation 10). When the point t is close to one of the rigid objects (like the t at the bottom of the figure), its influence in the non-linear term is also reduced. [Color version available online.]

Experimental validation

Data

We have applied our algorithm to a normal case (patient A) and four pathological cases with tumors (patients B through E). In all cases, we have one PET (of size 144 × 144 × 230 with resolution of 4 × 4 × 4 mm or 168 × 168 × 329 with resolution of 4 × 4×3 mm) and two CT volumes (of size 256× 256 × 55 with resolution of 1.42 × 1.42 × 5 mm to 512 × 512 × 138 with resolution of 0.98 × 0.98 × 5 mm), acquired during breath-hold in maximum inspiration and intermediate inspiration, from individual scanners. For the breathing model, ten meshes (corresponding to regularly distributed instants) are generated and compared with the PET. Each mesh contains more than 40,000 nodes. Here, the results are illustrated in two dimensions, but the algorithm is computed in three dimensions. In Figure 11, we compare the PET volume and two CT volumes: the closest simulated CT and the CT at end-inspiration.

Figure 11. Superimposition of the contours for the same coronal slice in the PET (black contour) and two CTs (grey contour) at two instants in the breathing cycle in patient B: (a) the closest to the PET (M_C), and (b) end-inspiration (M_N). The criterion C corresponds to the root mean square distance.

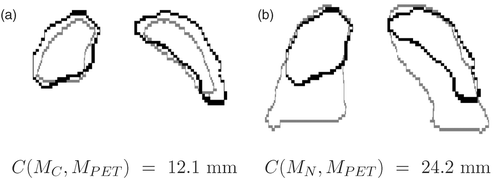
Criteria

To quantify the quality of the results, the volumes and surfaces of the segmented lungs in the original CT and the registered PET are compared. The original volume (or surface) of the CT is denoted as O, and R corresponds to the registered PET. The term |x| represents the cardinality of the set x. The volumes are compared using some classical measures:

• Percentage of false positives, denoted as FP, and false negatives, denoted as FN. These values correspond, respectively, to the percentage of voxels inside or not inside the lungs in the registered volume which are not inside or are inside the lungs in the original CT: FP(O,R) = [(|R| − |O∩R|)/|R|] and FN. These criteria evaluate the accuracy of the registration. Thus, for a correct result, FP and FN will take low values.

• Intersection/union ratio, denoted as IUR. This gives the ratio between corresponding volumes (correctly registered) and volumes that differ (false negatives and false positives): IUR. The higher this ratio, the higher the quality of the registration.

• Similarity index, denoted as SIM. This is defined by SIM(O,R) = [(2|O∩R|)/ < br/ > (|O| + |R|)]. This criterion must be as high as possible.

• Sensitivity, denoted as SEN. This measures the difference in volume between the original volume and the registered volume that has been correctly registered: SEN. If the registration is efficient, this criterion tends to 1.

• Specificity, denoted as SPE. This measures the difference in volume between the registered volume and a correctly registered volume: SPE. If the registration is performing well, this criterion tends to 1.

The surfaces are compared using the following criteria:

• Mean distance, denoted as MEAN. This is given by MEAN with , where D(o, R) = [min_r∈Rd(o, r)] and d is the Euclidean distance.

• Root mean square distance, denoted as RMS. This is defined by RMS with .

Results and discussion

The complexity of each step of the proposed algorithm is as follows (N denotes the number of voxels):

• For the segmentation steps, the complexity is linear for each segmentation, except when the “between” relation is used (segmentation of the heart). Its complexity is 0(N²). However, in practice, we noticed that the relation could be computed with sufficient precision by reducing the size of the image, thus reducing N and the computation time.

• For the estimation of the breathing model, the complexity can be decomposed into three parts: (i) the complexity of computing the displacement using the deformation kernel is 0(n²), where n is the number of surface nodes of the breathing model; (ii) the complexity of registering the end-expiration lung model with the end-inspiration lung model is 0(n²); and (iii) the complexity of estimating the deformation parameters is 0(nlog n). Finally, the selection of the closest instant has a linear complexity.

• For the registration, the complexity of the selection of the landmarks is linear; the complexity of the matching and the deformation depends on the number of landmarks N_ℒ and is respectively given by 0(NN_ℒ) and 0(N(N_ℒ + N_𝒪)), where N_𝒪 is the number of rigid objects.

In our tests, computation time for the whole process could take two hours: a few seconds for the segmentations, a few minutes for the landmark point selection, and approximately 90 minutes for the image volume registration process. Although this is not a constraint because we do not deal with a real-time application (this is not necessary for therapy planning), the computation time will be optimized in the future.

As illustrated in Figures 12 and 13 (one normal case and one pathological case), correspondences between landmark points on the original CT data set and the PET data set are more accurate with the breathing model (panels e and f in both figures) than without (panels b and c). Using the model, the corresponding points represent the same anatomical structures and the uniqueness constraint of the deformation field is enforced. In Table I, quantitative results are given and we can see that the PET volume is best registered with the proposed method BM-UNI. The quality of the results can be visually validated (panels f and i). In particular, the lower part of the lungs is better registered using the model: the lung contour in the registered PET data is closer to the lung contour in the original CT data, as shown in Figure 12 (panels j-l). In the pathological case, the tumor is well registered and not deformed, as illustrated in Figure 13. Here it can be observed that the registration using the breathing model avoids unrealistic deformations in the region between the lungs. In addition, distances between the registered PET lung surfaces and the original CT lung surfaces are lower when using the breathing model than when using the direct approach (cf. Table I).

Figure 12. Original PET (a) and CT (d and g) images in a normal case (patient A). Correspondences between selected points in a PET image and an end-inspiration CT image (g) are shown in (b) for the direct method, in (e) for the method with the breathing model and a non-uniform landmark points detection, and in (h) for the method with the breathing model and a pseudo-uniform landmark points selection (corresponding points are linked). PET data is shown in (c) with the direct method, in (f) with the method using the breathing model with a non-uniform landmark points distribution, and in (i) with the method using the breathing model and landmark points pseudo-uniformly distributed. The fourth row of images shows registration details on the bottom part of the right lung in a normal case: (j) is the end-inspiration CT; (k) shows PET data registered without the breathing model; and (l) shows PET data registered with the breathing model. The white crosses correspond to the same coordinates. The method using the breathing model provides a better registration of the lung surfaces. [Color version available online.]

Figure 13. Original PET (a) and CT (d and g) images in a pathological case (patient B: the tumor is surrounded by a white circle). The correspondences between the selected points in the PET image and the end-inspiration CT image (g) are shown in (b) for the direct method, in (e) for the method with the breathing model and a non-uniform landmark points detection, and in (h) for the method with the breathing model and a pseudo-uniform landmark points selection (corresponding points are linked). Registered PET is shown in (c) for the direct method, in (f) for the method with the breathing model with a non-uniform landmark point distribution, and in (i) for the method with the breathing model and landmark points pseudo-uniformly distributed. In panels (e) and (h) it can be observed that landmark points are better distributed with a uniform selection. The fourth row shows registration details in the region between the lungs in a pathological case: (j) is the end-inspiration CT; (k) is the PET registered without the breathing model; and (l) is the PET registered with the breathing model. The white crosses correspond to the same coordinates. The method using the breathing model avoids unrealistic deformations in this region. [Color version available online.]

Table I.  Quantitative results for a normal case and a pathological case (FP: false positives; FN: false negatives; IUR: Intersection/union ratio; SIM: similarity index; SEN: sensitivity; SPE: specificity; Mean: mean distance; RMS: root mean square distance, cf. Criteria sub-section). We compare the results obtained without the breathing model, with non-uniform selection, denoted as NOBM-NOUNI, and uniform selection, denoted as NOBM-UNI, and with the breathing model, with non-uniform selection, denoted as BM-NOUNI, and uniform selection, denoted as BM-UNI. Bold results indicate best results for each criterion and each case. The breathing-model version with uniform selection provided the lowest errors based on several criteria.

Method	FP	FN	IUR	SIM	SEN	SPE	Mean(mm)	RMS(mm)
Normal (Patient A)
ORIGINAL CT/PET	0.53	0.12	0.44	0.62	0.88	0.47	18.61	28.32
NOBM-NOUNI	0.66	0.01	0.4	0.57	0.99	0.4	15.7	20.7
NOBM-UNI	0.66	0.01	0.4	0.57	0.99	0.4	15.7	20.6
BM-NOUNI	0.45	0.02	0.54	0.7	0.98	0.54	11.4	16.4
BM-UNI	0.45	0.02	0.54	0.7	0.98	0.55	11.2	16.2
CLOSEST CT/PET	0.45	0.36	0.44	0.62	0.64	0.59	15.17	18.8
Pathological (Patient C)
ORIGINAL CT/PET	0.6	0.07	0.39	0.56	0.93	0.4	18.95	27.7
NOBM-NOUNI	0.63	0.03	0.37	0.54	0.97	0.37	17.7	26.5
NOBM-UNI	0.63	0.03	0.36	0.53	0.97	0.37	17.9	26.9
BM-NOUNI	0.66	0.05	0.33	0.5	0.95	0.34	15.2	23.7
BM-UNI	0.59	0.04	0.4	0.57	0.95	0.41	13.7	21.4
CLOSEST CT/PET	0.33	0.38	0.42	0.6	0.62	0.57	13.77	17.97

Finally, in Table I, we show that, for most of the criteria, the best results are obtained with BM-UNI. This method did not obtain the best results for the criteria FN and SEN. However, the variations of the values for these criteria are less than 2 × 10⁻², and we can conclude that FN and SEN are not very significant for comparing these four different methods. We also give the results obtained when we compare directly the original CT and the PET and the closest CT and the PET. This gives an indication of how the proposed method can improve the results. Ideally, the results obtained with the proposed methods should be better than those obtained from the comparison between the original CT and the PET. For the mean and RMS errors, this hypothesis is always respected and, moreover, the results are better than those obtained from the comparison between the closest CT and the PET.

Conclusion

In this paper, we have described the combination of a CT/PET landmark-based registration method and a breathing model to guarantee physiologically plausible deformations of the lung surface. The method consists of computing deformations guided by the breathing model. The originality of the proposed approach, which combines our landmark-based registration method including rigidity constraints and a breathing model, lies in its strong reliance on anatomical structures, its integration of constraints specific to these structures on the one hand and the pathologies on the other hand, and its accounting for physiological plausibility. Initial experiments (on one normal case and four pathological cases) show promising results, with significant improvement conferred by the breathing model. In particular, for the pathological cases, it avoids undesired tumor mis-registrations and preserves tumor geometry and intensity (this being guaranteed by the rigidity constraints, a main feature of the proposed approach).

In this work, we consider the impact of the physiology on lung surface deformation, based on reference data from normal human subjects. The methodology presented in this paper will further benefit from the inclusion of pathophysiology-specific data, once established. The use of normal lung physiology serves to demonstrate improvements in CT/PET registration using a physics-based 3D breathing lung model. Current ongoing work includes a deeper quantitative comparison and evaluation using a larger database in collaboration with clinicians. Future work will also include quantitative evaluations of the preservation of tumor geometry and intensity.

Future investigations are expected to be focused on refining the deformation model using pathophysiological conditions, and will include a more precise characterization of the tumor movement and its influence on the breathing model. Ultimately, validation of the breathing model in pathological cases should assess task-based performance on a clinical problem. It will also be a great improvement if the variability of the breathing model for different patients can be taken into account by using different typical breathing models that can account - as far as possible - for all the individual differences. Moreover, planned future work includes the use of different criteria for the selection of the appropriate CT (see Simulated CT selection sub-section): the RMS distance is a global criterion that does not take into account local differences or similarities between the surfaces. Another improvement would be for the selection of landmark points to include points undergoing significant displacements during respiration, and the use of these points to guide the registration procedure.

Acknowledgments

This work was partly funded by ANR (Agence Nationale pour la Recherche: project MARIO, 5A0022), Segami Corporation, France, and the Florida Photonics Center of Excellence in Orlando, Florida. The authors would like to thank Val-de-Grâce Hospital, Paris, France, and the MD Anderson Cancer Center, Orlando, Florida, for the images. They would also like to thank Hassan Khotanlou for his helpful remarks and corrections.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.