Use of the harmonic mean to the determination of dissociation constants of stereoisomeric mixtures of biologically active compounds

Abstract

Herein we introduce the derivation of a mathematical expression to evaluate the dissociation constant of a mixture of stereoisomers in equal amounts (K_dMIX), when the corresponding dissociation constants (K_d) or medium response (MR₅₀) of the pure stereoisomers are known; the final equation takes the form of the harmonic mean. In order to validate the equation, we carried out a bibliographic search of experimental data of enantiomeric molecules with biological activity, considering the K_d’s or MR₅₀’s of the isolated enantiomers as well as that of the racemate. The comparisons between the experimental dissociation constants of the mixtures (K_dEXP or MR_50EXP) and the calculated values (K_dMIX or MR_50MIX) were consistent; the similarity between these values is supported through statistical analyses of group comparison and simple linear correlation. The equation we obtained, which corresponds to the harmonic mean, was used to predict the values of K_dMIX (or MR_50MIX) or K_d (or MR₅₀) in systems when only two of the experimental values are known: either the dissociation constants of both enantiomers or the K_d (or MR₅₀) of one of the enantiomers and dissociation constant of the racemate.

• Dissociation constants
• enantiomers
• harmonic mean
• medium
• racemate
• response

Introduction

A large fraction of drugs or substances with biological activity corresponds to organic molecules that can exist in two or more stereoisomeric forms. The synthesis of these compounds with a particular stereochemistry presents a challenge to chemists as well as to health specialists. Currently, a high fraction of the active principles of pharmaceutical drugs is commercialized as racemates1–3. Nevertheless, in the last decade there has been a substantial increment in the distribution of enantiomerically pure substances1, as it has been shown that there is usually a pharmacokinetic and pharmacodynamic advantage of using only one enantiomer (eutomer) over the other (distomer)4–6. On the other hand, the distomer may have a different kind of biological activity, even toxicity5,7, or it may have the same activity but different affinity to the receptor.

Herein we present the deduction of an equation intended to recognize the relationship between the dissociation constants of the individual components of a mixture of stereoisomers (K_d), particularly of a racemate, and the dissociation constant of the mixture as a whole (K_dMIX). It is shown that the expression has the same form as that corresponding to the harmonic mean.

Methods

Bibliographic search

The revision focused on data reported in the last four decades on dissociation constants K_d, IC₅₀ or ED₅₀ with Hill coefficients equal 1 (n_H = 1) of racemates as well as of the pure enantiomers. Particular emphasis was put on searching for data obtained on the same receptor and under the same methodology.

Calculation of K_dMIX

This calculation was carried out using the equation proposed in this work (harmonic mean) starting from the K_d, IC₅₀ or ED₅₀ values reported for the pure enantiomers.

Validation and statistical analysis

The validation process was carried out through comparison of the K_d, IC₅₀ or ED₅₀ experimental values with the calculated K_dMIX or MR_50MIX values by means of the Mann--Whitney U test, with a statistically significant value of p < 0.05. The group comparison was performed through the normalized values which were determined by means of the following expressions: where K_dEXP or MR_50EXP corresponds to the experimental dissociation constant or medium response of the racemate, K_dMIX or MR_50MIX to the value calculated through the proposed equation (harmonic mean), and K_dEXPsmallest or MR_{50EXPsmallest} to the experimental value of the pure enantiomer with the highest affinity for the receptor. To determine the sensitivity of the prediction of K_dMIX (or MR_50MIX), a correlation was carried out between pK_dEXP (or pMR_50EXP) and pK_dMIX (or pMR_50MIX) through a simple regression analysis validated by Student’s t test, where p < 0.05 is statistically significant. Finally, a covariance analysis between the slopes of both curves was carried out by Student’s t test, where p < 0.05 is statistically significant.

Results

The binding between a ligand L and a receptor R, leading to the formation of a ligand–receptor complex (R–L) can be described by the following equilibrium (8):

One way to evaluate the affinity between ligand and receptor is through the value of the dissociation constant K_d, which measures the tendency of the ligand–receptor complex to dissociate. The dissociation constant (Equation (1)) corresponds to the equilibrium constant for the inverse of the process described above: where [R–L] is the concentration of the ligand–receptor complex; [R] and [L] are the concentrations of the free ligand and receptor, respectively. Low values of K_d indicate high affinity between ligand and receptor.

As an equilibrium constant, K_d is related to the Gibbs free energy of the ligand–receptor binding process shown before according to Equation (2). This energy is, in turn, determined by the intermolecular interactions that govern the complexation between both fragments8.

It is well known that many biologically active substances are chiral and that they are usually obtained as racemates. In this case, we formally have two different substances competing for a given receptor. If we assume that each enantiomer is expected to have an independent affinity for the chiral receptor, we can expect the racemate to have a value of the dissociation constant, K_dMIX, corresponding to some kind of average of the K_d values of both enantiomers. However, how do we obtain this average? It is expected that the K_d of the enantiomer with the higher affinity for the receptor contributes the most to the value of K_dMIX; thus, the latter could be defined as the sum of the weighted contributions of the individual K_d values of the enantiomers. According to the definition of the weighted mean, , we can propose the expression shown in Equation (3)9. where K_d1 and K_d2 are the dissociation constants of each enantiomer, and w₁ and w₂ correspond to the weight in which each enantiomer contributes to the overall complexation of the mixture to the receptor. If we assume that the total number of receptors is constant, and that each enantiomer of the racemic mixture will bind to a fraction of this number, we can expect that w₁ + w₂ = 1, so that Equation (3) becomes Equation (4).

Once the expression for K_dMIX has been defined, it is fundamental to describe the expressions corresponding to the weights (w_i), which are defined in terms of the K_d’s of the pure enantiomers and of the relationship between them as shown in Equation (5):

It can be seen that each weight w_i corresponds to the fraction of the binding of enantiomer j to the receptor, with respect to enantiomer i, in relation to the overall binding of both enantiomers to the receptor; simplification of Equation (5) leads to Equation (6).

This expression can be further simplified to Equation (7).

Generalization

We can now turn our attention to the case in which we have three or more molecules competing for binding to the same receptor, as would be the case of a mixture of stereoisomers of molecules with more than one stereogenic center. According to the above (Equation (4)), K_dMIX would be described by Equation (8) for three stereoisomers present in equal amounts in a mixture:

In this case, the definition of the weights is the same as before, however, in order to obtain w_i, now we have to consider the fraction of binding of isomers j and k with respect to isomer i. This can be done by obtaining first the fraction of binding of isomer j with respect to isomer k (or isomer k with respect to isomer j) as done in the two-component mixture (Equation (5)), and then referring this result to isomer i, as shown in Equation (9).

By substituting Equation (9) into Equation (8), and carrying out the corresponding algebra we obtain Equation (10), which describes the average binding of the mixture as a function of the individual binding constants of its components.

It can be shown that this expression can be further simplified to Equation (11).

Note that Equations (7) and (11) describe the average dissociation constants of two- and three-component mixtures, and that these equations are particular cases of a more general case, which is described by Equation (12) for an n-component mixture.

It can be readily seen that Equation (12) is the same as that of the harmonic mean (H)9 of a set of n numbers x_i (Equation (13)) so that K_dMIX is the harmonic mean of the individual dissociation constants of the components of the mixture.

Discussion

The harmonic mean has been used for a long time to explain the total lethal effect on rats of mixtures of chemicals used extensively in industry10. Similarly, the effect of a large variety of mixtures of toxic substances on laboratory animals has been studied and explained statistically through the use of the harmonic mean for mixtures of two or more components11. The harmonic mean has already been used in other cases where dissociation constants are involved. For example, Raffa used the harmonic mean to relate the K_d of mutant receptors or ligands to the K_d of the wild-type species, something that could not be achieved by neither the arithmetic nor the geometric means12. In studies more related to ours, Chou and Talalay described in a broad and detailed study the average effect of mixtures of mutually exclusive enzymatic inhibitors, which follow a first-order kinetics, using the harmonic mean13. Houghten et al. used the harmonic mean to predict the IC₅₀ value of mixtures of components derived from combinatorial libraries for which the corresponding individual IC₅₀ values as well as that of the mixture were known14. We should point out that in both instances the harmonic mean was applied directly, without the mathematical derivation that we introduced earlier.

With the goal of validating Equation (12) we carried out a search of experimental data reported in the literature, considering only those reports containing average responses for the pure enantiomers and for the racemates of substrates onto different receptors. For each case, we calculated K_dMIX or MR_50MIX from the corresponding experimental values of dissociation constants (Table 1) or half maximal concentrations (MR₅₀) (Table 2) and compared them to the experimental average response of the racemates.

Table 1. Comparison between the calculated K_dMIX with the K_d experimental values of racemates.

Compounds	Receptor	Isomer	Kd (exp)*	KdMIX (calcd)^a	References
Nimodipine	CaV1.2	(+)	2.40 nM		15
BAY E 9736	CaV1.3	(−)	1.04 nM
		(±)	1.44 nM	1.45 nM
Nitrendipine BAY E 5009	CaV1.2 CaV1.3	(+)	8.8 nM		15
		(−)	0.43 nM
		(±)	0.93 nM	0.82 nM
BAY E 6927	CaV1.2 CaV1.3	(+)	27.5 nM		15
		(−)	0.09 nM
		(±)	0.22 nM	0.18 nM
Bay k 8644	CaV1.2	(+)	13.9 ± 1.2 nM		16
		(−)	2.47 ± 0.34 nM
		(±)	5.9 ± 1.7 nM	4.19 nM
Metoprolol	β1	S	18.62 ± 3.83 nM		17
		R	10 000.0 ± 1290.3 nM
		(±)	47.86 ± 12.38 nM	37.17 nM
Metoprolol	β2	S	0.52 ± 0.06 µM		17
		R	30.19 ± 5.65 µM
		(±)	1.15 ± 0.21 µM	1.02 µM
Salbutamol	Sulfation by M form hepatic PST	(+)	1394 µM		18
		(−)	103 µM
		(±)	129 µM	191.8 µM
Salbutamol	Sulfation by the 100 000 g cytosol of the jejunal mucosa PST	(+)	889 ± 73 µM		18
		(−)	95 ± 11 µM
		(±)	140 ± 21 µM	171.6 µM
Salbutamol	Sulfation by the platelet homogenate PST	(+)	1190 ± 285 µM		18
		(−)	141 ± 21 µM
		(±)	251 ± 34 µM	252.1 µM
Naloxone	κ	(+)	19 000 nM		19,20
		(−)	9 nM
		(±)	20 nM	17.99 nM
CP-96,345	CaV1.2 CaV1.3	2 S,3 S	22.5 (−2.2, +2.4) nM		21
CP-96,344		2 R,3 R	37.3 (−0.7, +0.7) nM
CP-96,345		(±)	29.2 (−2.3, +2.4) nM	28.06 nM
Terfenadine	KV1.5	S	1.16 ± 0.20 µM		22
		R	1.19 ± 0.09 µM
		(±)	0.81 ± 1.10 µM	1.17 µM
8-OH-DPAT	D2	(+)	1082 ± 222 nM		23
		(−)	12 506 ± 2917 nM
		(±)	1746 ± 218 nM	1991.7 nM
8-OH-DPAT	D3	(+)	198 ± 82 nM		23
		(−)	2178 ± 130 nM
		(±)	361 ± 41 nM	363.0 nM
8-OH-DPAT	5-HT1A	(+)	0.47 ± 0.11 nM		23
		(−)	0.64 ± 0.14 nM
		(±)	0.58 ± 0.03 nM	0.54 nM
Ketamine	µ	S(+)	4.54 ± 0.01 µM		24
		R(−)	4.08 ± 0.05 µM
		(±)	4.38 ± 0.02 µM	4.29 µM
Ketamine	κ	S(+)	4.63 ± 0.03 µM		24
		R(−)	4.22 ± 0.03 µM
		(±)	4.55 ± 0.04 µM	4.41 µM
Ketamine	δ	S(+)	3.69 ± 0.01 µM		24
		R(−)	4.54 ± 0.01 µM
		(±)	3.57 ± 0.02 µM	4.07 µM
THC	NR3A1 (ERα)	SS	39.0 nM		25
		RR	9.0 nM
		(±)	13.0 nM	14.6 nM
THC	NR3A2 (ERβ)	SS	70.0 nM		25
		RR	3.6 nM
		(±)	3.6 nM	6.84 nM
Fenfluramine	5HT2A	(+)	11 107 ± 1354 nM		26
		(−)	5463 ± 352 nM
		(±)	5216 ± 2.5 nM	7323.8 nM
Fenfluramine	5HT2B	(+)	5099 ± 690 nM		26
		(−)	5713 ± 1344 nM
		(±)	4134 ± 753 nM	5388.6 nM
Fenfluramine	5HT2C	(+)	6245 ± 514 nM		26
		(−)	3415 ± 542 nM
		(±)	3183 ± 374 nM	4415.5 nM
Norfenfluramine	5HT2A	(+)	1516 ± 88 nM		26
		(−)	3841 ± 361 nM
		(±)	2316 ± 163 nM	2173.9 nM
Norfenfluramine	5HT2B	(+)	11.2 ± 4.3 nM		26
		(−)	47.8 ± 18.0 nM
		(±)	52.1 ± 12.3 nM	18.1 nM
Norfenfluramine	5HT2C	(+)	324 ± 7.1 nM		26
		(−)	814 ± 58 nM
		(±)	557 ± 36 nM	463.5 nM
Cetirizine	H1	S	79.4 ± 16.3 nM		27
		R	3.16 ± 0.64 nM
		(±)	6.31 ± 1.29 nM	6.08 nM
Hydroxyzine	H1	S	31.6 ± 6.5 nM		27
		R	1.0 ± 0.2 nM
		(±)	1.99 ± 0.40 nM	1.94 nM
trans-H2-PAT	H1 (versus [^3H]- mepyramine)	(+)	23.0 ± 2.0 nM		28
		(−)	1.15 ± 0.36 nM
		(±)	1.53 ± 0.06 nM	2.19 nM
trans-H2-PAT	H1 (versus [^3H]- (−)-trans-H2-PAT)	(+)	11.54 ± 0.13 nM		28
		(−)	0.58 ± 0.10 nM
		(±)	1.37 ± 0.04 nM	1.10 nM
trans-H2-PAT	H1 (versus [^3H]- mepyramine)	(+)	42.4 ± 1.60 nM		28
		(−)	2.50 ± 0.17 nM
		(±)	4.26 ± 0.25 nM	4.72 nM
trans-H2-PAT	H1 (versus [^3H]-(−)- trans-H2-PAT)	(+)	29.9 ± 4.70 nM		28
		(−)	1.65 ± 0.14 nM
		(±)	2.49 ± 0.27 nM	3.12 nM
cis-H2-PAT	H1 (versus [^3H]- mepyramine)	(+)	53.79 ± 1.39 nM		28
		(−)	3.92 ± 0.18 nM
		(±)	10.89 ± 0.14 nM	7.31 nM
cis-H2-PAT	H1 (versus [^3H]-(−)- trans-H2-PAT)	(+)	77.7 ± 1.07 nM		28
		(−)	4.91 ± 0.03 nM
		(±)	7.87 ± 0.63 nM	9.23 nM
cis-H2-PAT	H1 (versus [^3H]- mepyramine)	(+)	129 ± 13 nM		28
		(−)	8.91 ± 0.76 nM
		(±)	13.6 ± 0.8 nM	16.66 nM
cis-H2-PAT	H1 (versus [^3H]-(−)- trans-H2-PAT)	(+)	122 ± 9 nM		28
		(−)	6.31 ± 0.23 nM
		(±)	14.7 ± 0.46 nM	12.00 nM
Citalopram	SERT	R	161 nM		29
		S	3.9 nM
		(±)	7.6 nM	7.61 nM
Omeprazole	5-Hydroxilation by HLM	S R (±)	7.4 µM 1.4 µM 2.9 µM	2.35 µM	30
Omeprazole	5-Hydroxilation by CYP2C19	S	8.9 µM		30
		R	1.6 µM
		(±)	2.5 µM	2.71 µM
Omeprazole	5-Hydroxilation by CYP3A4	S	47 µM		30
		R	37 µM
		(±)	42 µM	41.40 µM
Omeprazole	5′-O-Demethylation by HLM	S R (±)	4.7 µM 1.9 µM 1.9 µM	2.70 µM	30
Omeprazole	5′-O-Demethylation by CYP3A4	S R (±)	51 µM 83 µM 59 µM	63.18 µM	30
Omeprazole	3-Hydroxilation by HLM	S R (±)	15 µM 20 µM 17 µM	17.14 µM	30
Omeprazole	5-Hydroxilation by CYP3A4	S R (±)	15 µM 26 µM 20 µM	19.02 µM	30
Ibuprofen	I-FABP	S	135 ± 4.0 µM		31
		R	63 ± 1.4 µM
		(±)	96 ± 1.8 µM	85.90 µM
Tramadol	µ	(+)	1.3 µM		32
		(−)	24.8 µM
		(±)	2.1 µM	2.47 µM
Tramadol	5-HT	(+)	0.53 µM		32
		(−)	2.35 µM
		(±)	0.99 µM	0.86 µM
Tramadol	α	(+)	2.51 µM		32
		(−)	0.43 µM
		(±)	0.78 µM	0.73 µM
Mescaline analogue	5-HT2A	R-(+)	69 ± 20 nM		33
		S-(−)	1120 ± 180 nM
		(±)	130 ± 20 nM	129.99 nM
AM1241	CB2	S	658 ± 44.2 nM		34
		R	15.1 ± 4.18 nM
		(±)	28.7 ± 2.01 nM	29.52 nM
AM1241	CB2	S	893 ± 58.5 nM		34
		R	12.0 ± 1.27 nM
		(±)	26.7 ± 0.44 nM	23.68 nM
AM1241	CB2	S	577 ± 58.4 nM		34
		R	13.2 ± 0.76 nM
		(±)	23.8 ± 4.36 nM	25.81 nM
SPFF	β1	(+)	33.62 ± 2.52 µM		35
		(−)	2.20 ± 0.12 µM
		(±)	3.87 ± 0.25 µM	4.13 µM
SPFF	β2	(+)	14.58 ± 0.24 µM		35
		(−)	0.09 ± 0.01 µM
		(±)	0.52 ± 0.02 µM	0.18 µM
Fluoxetine	CYP2C19	S	46.7 ± 4.0 µM		36
		R	6.5 ± 0.6 µM
		(±)	13.7 ± 1.8 µM	11.4 µM
DPN	NR3A1 (ERα)	S	20.8 ± 2.9 nM		37
		R	147 ± 12.3 nM
		(±)	48.1 ± 3.5 nM	36.4 nM
DPN	NR3A2 (ERβ)	S	0.27 ± 0.05 nM		37
		R	1.82 ± 0.21 nM
		(±)	0.61 ± 0.07 nM	0.47 nM

PST: phenol-sulfotransferase; 8-OH-DPAT: 8-hydroxy-2-(di-n-propilamino)tetralin; THC: tetrahydrochrisene; HPU: N³-α-hydroxy-β-phenethyluridine; trans-H₂-PAT: trans-1-phenyl-3-N,N-dimethylamino-1,2,3,4-tetrahydronaphtalene; cis-H₂-PAT: cis-1-phenyl-3-N,N-dimethylamino-1,2,3,4-tetrahydronaphtalene; HLM: human liver microsomes; I-FABP: intestinal fatty acid-binding protein; SPFF: [2-(4-amino-3-chloro-5-trifluomethyl-phenyl)-2-tert-butylamino-ethanol hydrochloride]; DPN: diarylpropionitrile.

*Statistical analysis between normalized experimental values (N = K_dEXP/K_dEXPsmallest) and ^aCalculated values (N = K_dMIX/K_dEXPsmallest) carried out with the Mann--Whitney U test (p = 0.802).

Table 2. Comparison between the calculated MR_50MIX with the medium response (MR₅₀) experimental values of racemates.

Compounds	Receptor	Isomer	MR50 (exp)^a	MR50MIX (calcd)*	References
Quinuclidine acetate	M	(+)	0.15 ± 0.05 µM		38
		(−)	3.00 ± 1.00 µM
		(±)	0.55 ± 0.15 µM	0.28 µM
APB	GluN	L(+)	2.24 µM		39
		D(−)	30.06 µM
		(±)	3.61 µM	4.16 µM
AA	GluN	L	3.00 µM		39
		D	16.18 µM
		(±)	6.13 µM	5.06 µM
2A5PP	GluN	L(+)	20.0 µM		39
		D(−)	126.0 µM
		(±)	39.8 µM	34.50 µM
2A7PP	GluN	L(+)	18.96 µM		39
		D(−)	100.00 µM
		(±)	32.60 µM	31.87 µM
FTC	Inverse-transcriptase on CFU-GM	(+)	7.5 ± 3.9 µM		40
		(−)	50.0 ± 30 µM
		(±)	34.0 ± 12 µM	13.04 µM
YM022	CCK2	R	0.055 (0.046–0.067) nM		41
		S	10.7 (9.8–11.7) nM
		(±)	0.11 (0.10–0.12) nM	0.109 nM
Ofloxacin	DNA-gyrase	S	1.5 µg/mL		42
		R	75.0 µg/mL
		(±)	2.6 µg/mL	2.94 µg/mL
Ibuprofen	PGHS-1	S	2.1 ± 1.3 µM		43
		R	34.9 ± 13.2 µM
		(±)	6.5 ± 2.5 µM	3.96 µM
Physostigmine	AChE of cortex	(+)	22 000 nM		44
		(−)	31 nM
		(±)	72 nM	61.91 nM
Physostigmine	AChE of caudate	(+)	26 000 nM		44
		(−)	35 nM
		(±)	74 nM	69.90 nM
Physostigmine	AChE of erythrocyte	(+)	25 000 nM		44
		(−)	28 nM
		(±)	70 nM	55.93 nM
Physostigmine	BuChE of cortex	(+)	26 000 nM		44
		(−)	129 nM
		(±)	265 nM	256.72 nM
Physostigmine	BuChE of plasma	(+)	4000 nM		44
		(−)	15 nM
		(±)	35 nM	29.88 nM
NFPS	GlyT1a	(+)	0.7 ± 0.1 nM		45
		(−)	30 ± 11 nM
		(±)	9.8 ± 0.1 nM	1.37 nM
Methadone	GluN1/2 A (NMDA)	S(+)	9.4 (7.3–12.1) µM		46
		R(−)	0.15 (0.08–0.25) µM
		(±)	3.6 (2.8–4.5) µM	0.29 µM
Methadone	GluN1/2B (NMDA)	S(+)	4.3 (3.6–5.3) µM		46
		R(−)	4.7 (3.9–5.6) µM
		(±)	3.0 (2.5–3.5) µM	4.49 µM
Methadone	GluN1/2 C (NMDA)	S(+)	10.8 (8.8–13.2) µM		46
		R(−)	25.7 (20.8–31.8) µM
		(±)	12.1 (10.0–14.8) µM	15.21 µM
Methadone	GluN1/2D (NMDA)	S(+)	14.6 (11.3–18.9) µM		46
		R(−)	22.2 (17.0–29.0) µM
		(±)	8.9 (7.0–11.4) µM	17.61 µM
Citalopram	Rat brain synaptosomes SERT	R S (±)	275 nM 2.1 nM 3.9 nM	4.17 nM	29
CPG	M	S(+)	1263.12 ± 131.64 nM		47
		R(−)	46.49 ± 1.27 nM
		(±)	271.37 ± 72.3 nM	89.68 nM
Fluoxetine	CYP2C19	S R (±)	93.00 ± 8.71 µM 21.00 ± 0.57 µM 27.00 ± 5.00 µM	34.26 µM	36
Fluoxetine	CYP2C19	S R (±)	3.36 ± 0.34 µM 4.03 ± 0.35 µM 3.00 ± 0.62 µM	3.66 µM	36
Fluoxetine	CYP2C19	S R (±)	28.33 ± 2.60 µM 5.16 ± 0.38 µM 9.33 ± 1.56 µM	8.73 µM	36

APB: 2-amino-4-phosphobutyrate; AA: α-aminoadipate; 2A5PP: 2-amino-5-phosphonopentanoate; 2A7PP: 2-amino-7-phosphonoheptanoate; FTC: 2′,3′-dideoxy-5-fluoro-3′-thiacytidine; CFU-GM: colony forming unit-granulocyte/macrophages; PGHS-1: prostaglandin endoperoxide synthase constitutive; NFPS: (N-[3-(4′-fluorophenyl)-3-(4′-phenylphenoxi)propyl]sarcosine; CPG: phencynonate hydrochloride.

*Statistical analysis between normalized experimental values (N = MR_50EXP/MR_{50EXPsmallest}) and ^aCalculated values (N = MR_50MIX/MR_{50EXPsmallest}) carried out with the Mann--Whitney U test (p = 0.053).

The experimental average responses of the racemates of the substrates summarized in Table 1 are very similar to the calculated values, independently of the pharmacologic or biochemical relationship to the receptor: agonist, antagonist, substrate, inhibitor, etc. As expected and according to the definition of the harmonic mean9, in all cases the calculated values of K_dMIX are closer to that of the enantiomer with the smallest average response, which is that with the highest affinity to the receptor. It can also be seen that the calculated K_dMIX values are not very much affected by the largest K_d values of the stereoisomer with the lowest affinity to the receptor.

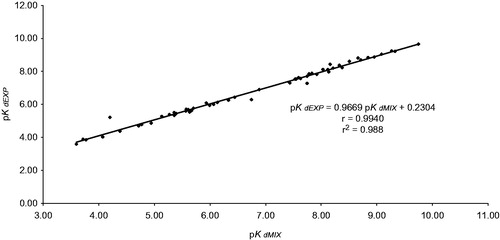
The statistical analysis of the correlation between pK_dEXP and pK_dMIX shows a linear relationship with a slope value very near 1.0; this means that prediction of K_d through the harmonic mean leads to values of practically the same magnitude as those of K_dEXP (Figure 1).

Figure 1. Correlation between pK_dEXP and pK_dMIX. Statistical simple linear regression analysis; b = 0.2304 ± 0.3008 at 95.0% confidence interval (p > 0.05); m = 0.9669 ± 0.0291 at 95.0% confidence interval (p < 0.001) and r = 0.9885 (p < 0.001) by Student’s t test.

Similarly, we analyzed those results where average effects were reported as IC₅₀ or EC₅₀ (both also known as MR₅₀). We performed a correlation and a simple linear regression analysis between MR_50EXP and MR_50MIX (Figure 2) which do not show significant differences between theoretical and normalized experimental values.

Figure 2. Correlation between pMR_50EXP and pMR_50MIX. Statistical simple linear regression analysis; b = 0.3034 ± 0.5510 at 95.0% confidence interval (p > 0.2); m = 0.9311 ± 0.0869 at 95.0% confidence interval (p < 0.001) and r = 0.9782 (p < 0.001) by Student’s t test.

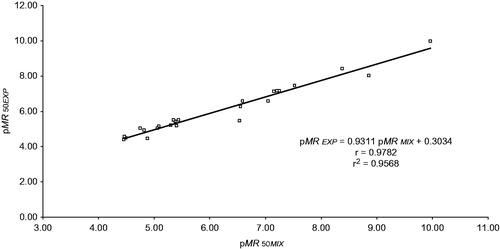
As before, pMR_50EXP and pMR_50MIX show a linear correlation with a slope very close to 1.0; again, prediction of MR₅₀ through the harmonic mean leads to values of practically the same magnitude as those of MR_50EXP. Thus the harmonic mean can predict satisfactorily K_d values as well as MR₅₀ values.

The K_d and MR₅₀ values shown in Tables 1 and 2 were obtained through in vitro experiments. Both types of results are not necessarily equivalent between each other48; however, their values can be predicted independently through the harmonic mean. Therefore, we performed a covariance analysis between the straight lines in Figures 1 and 2, to show whether there is similarity between the slopes (Figure 3).

Figure 3. ♦: Dissociation constants (pK_d); □: Medium responses (pMR₅₀). ANCOVA: the difference of slopes between both groups is not large enough to exclude the possibility that the difference is due to random sampling variability; there is no statistically significant difference (p > 0.5). One way ANOVA: the difference of slopes between both groups is not large enough to exclude the possibility that the difference is due to random sampling variability; there is no statistically significant difference (p > 0.25).

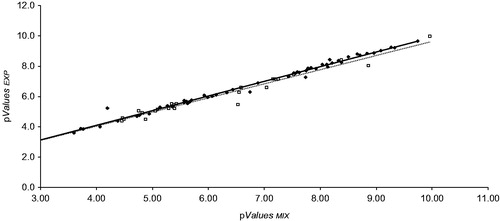
Based on analysis of covariance (ANCOVA) and one-way analysis of variance (ANOVA) for both sets data, we conclude that the harmonic mean predicts with the same magnitude and accuracy the K_dMIX and MR_50MIX values starting from experimental data, regardless of the type of variable (K_d or MR₅₀), provided these variables describe the affinity of the components of the mixture to the same site of the receptor or enzyme.

In addition, in Table 3 we have estimated K_dMIX or MR₅₀ for the racemic mixtures of a series of compounds using Equation (12), starting from the reported experimental K_d or MR₅₀ values of the pure enantiomers.

Table 3. Prediction of K_dMIX or MR_50MIX calculated from K_d or MR₅₀ experimental values of pure enantiomers.

Compounds	Receptor	Isomer	Kd or MR50 (exp)	KdMIX or MRMIX50 (calcd)	References
Adrenaline	β1 of heart	(+)	2000 ± 450 nM	279.06 nM	49
		(−)	150 ± 30 nM
Adrenaline	β2 of lung	(+)	2000 ± 500 nM	208.53 nM	49
		(−)	110 ± 13 nM
Noradrenaline	β1 of heart	(+)	8100 ± 1000 nM	634.16 nM	49
		(−)	330 ± 50 nM
Noradrenaline	β2 of lung	(+)	26 000 ± 1800 nM	2018.48 nM	49
		(−)	1050 ± 250 nM
Isoproterenol	β1 of heart	(+)	530 ± 150 nM	13.81 nM	49
		(−)	7 ± 1 nM
Isoproterenol	β2 of lung	(+)	780 ± 30 nM	128.47 nM	49
		(−)	70 ± 19 nM
Propranolol	β1 of heart	(+)	79 ± 13 nM	0.91 nM	49
		(−)	0.46 ± 0.03 nM
Propranolol	β2 of lung	(+)	30 ± 2 nM	0.43 nM	49
		(−)	0.22 ± 0.02 nM
Glutamate	GluN	D	18.10 µM	3.10 µM	39
		L	1.70 µM
Aspartate	GluN	D	56.20 µM	12.40 µM	39
		L	6.97 µM
Butaclamol	D2	(+)	1300 ± 240 nM	73.84 nM	50
		(−)	38 ± 2 nM
Ketoprofen	PGHS-1	R	7.5 ± 0.73 µM	0.21 µM	51
		S	0.11 ± 0.04 µM
Ketoprofen	PGHS-2	R	20.6 ± 0.45 µM	0.35 µM	51
		S	0.18 ± 0.06 µM
Nicotine	N1	(+)	99 nM	6.01 nM	52
		(−)	3.1 nM
Bridge-Nicotine	N1	(+)	39 µM	28.93 µM	52
		(−)	23 µM
7-OH-DPAT	D2	(+)	89 ± 12 nM	169.52 nM	23
		(−)	1780 ± 430 nM
7-OH-DPAT	D3	(+)	2.4 ± 0.54 nM	4.60 nM	23
		(−)	55.6 ± 8 nM
7-OH-DPAT	5-HT1A	(+)	51 ± 13 nM	85.53 nM	23
		(−)	265 ± 42 nM
α-Methylhistamine	H3	R(−)	140 ± 10 nM	268.92 nM	53
		S(+)	3400 ± 300 nM
ucb 29992	H1	R	5.01 ± 2.4 nM	9.28 nM	27
ucb 29993		S	63.09 ± 14.65 nM
Chlorpheniramine	CHO-H1 versus [^3H]-mepyramine	(+)	4.81 ± 0.05 nM	9.49 nM	28
		(−)	361 ± 40 nM
Chlorpheniramine	CHO-H1 versus [^3H]-(−)-trans-H2-PAT	(+)	2.67 ± 0.23 nM	5.27 nM	28
		(−)	211 ± 9 nM
Aceclidine	M2	R	17 ± 0.11 µM	3.24 µM	54
		S	1.79 ± 0.07 µM
3 F-GABA	ρ1GABAC	R	11.10 ± 1.24 µM	13.93 µM	55
		S	18.72 ± 0.60 µM
3 F-GABA	ρ2GABAC	R	2.92 ± 0.66 µM	4.59 µM	55
		S	10.76 ± 1.90 µM

7-OH-DPAT: 7-hydroxy-2-(di-n-propilamino)tetralin; PGHS-1: prostaglandin endoperoxide synthase constitutive; PGHS-2: prostaglandin endoperoxide synthase inducible; 3 F-GABA: 3-fluoro-γ-aminobutiric acid.

On the other hand, when the experimental values of K_d of only one of the enantiomers and of the racemic mixture of a compound are available, it is possible to predict the K_d or EC₅₀ values of the other enantiomer. Table 4 shows examples of this for a number of cases.

Table 4. Prediction of K_d or MR₅₀ of a pure enantiomer from the experimental values of K_d or MR₅₀ of the other pure enantiomer and K_d or MR₅₀ of the racemate.

Compounds	Receptor	Isomer	Kd or MR50 (exp)	Kd or MR50 (calcd)	References
DOI	5-HT2	R(−)	1.5 ± 0.5 nM		56
		S(+)	—	4.93 nM
		(±)	2.3 ± 1.0 nM
DOI	5-HT2	R(−)	30.0 ± 5.1 nM		56
		S(+)	—	112.85 nM
		(±)	47.4 ± 16.8 nM
Betaxolol	NaV1 Cerebrocortical	(+)	—	8.77 µM	57
		(−)	11.1 µM
		(±)	9.8 µM
Citalopram	SERT	R	—	5890.47 nM	58
		S	29.8 ± 5.2 nM
		(±)	59.3 ± 6.7 nM
Isradipine	Cav1.2 DHP binding domain WT	(+)	—	0.216 nM	59
		(−)	35.2 ± 7.4 nM
		(±)	0.43 ± 0.03 nM
Ketamine	GluN2A (NMDA)	(+)	—	0.167 µM	60
		(−)	16 µM
		(±)	0.33 µM
Ketamine	GluN2B (NMDA)	(+)	—	0.172 µM	60
		(−)	1.6 µM
		(±)	0.31 µM
Ketamine	GluN2C (NMDA)	(+)	—	0.332 µM	60
		(−)	1.1 µM
		(±)	0.51 µM
Ketamine	GluN2D (NMDA)	(+)	—	0.574 µM	60
		(−)	1.5 µM
		(±)	0.83 µM

DOI: 4-iodo derivative of 2,5-DMA.

Conclusions

We have deduced the expression corresponding to the average dissociation constant of a mixture of isomers K_dMIX, as a function of the weights of the K_d’s of individual components of the mixture. We come to the conclusion that K_dMIX corresponds to the harmonic mean of the K_d’s of the components.

When the values of K_dMIX obtained with the harmonic mean equation are compared with the experimental values reported in the literature for the K_d of racemic mixtures, a close match between both sets is observed. When only the K_d values of the pure enantiomers are known, it is possible to predict the value of the K_d of the racemic mixture. If only the K_d value of one of the enantiomers is known, along with the K_d value of the racemic mixture, it is possible to predict the K_d (or MR₅₀) value of the other enantiomer.

Declaration of interest

The authors state no conflicts of interest.

DQZ, HAJV and JTF are fellows of the COFAA-IPN and EDI-IPN fellowship programs.