Dynamics and shape of large fire ant rafts

Abstract

To survive floods, fire ants link their bodies together to build waterproof rafts. Such rafts can be quite large, exceeding 100,000 individuals in size. In this study, we make two improvements on a previously reported model on the construction rate of rafts numbering between 3,000 and 10,000 individuals. That model was based upon experimental observations of randomly-directed linear ant trajectories atop the raft. Here, we report anomalous behavior of ants atop larger rafts of up to 23,000 ants. As rafts increase in size, the behavior of ants approaches diffusion, which is in closer alignment with other studies on the foraging and scouting patterns of ants. We incorporate this ant behavior into the model. Our modified model predicts more accurately the growth of large rafts. Our previous model also relied on an assumption of raft circularity. We show that this assumption is not necessary for large rafts, because it follows from the random directionality of the ant trajectories. Our predicted relationship between raft size and circularity closely fits experimental data.

Keywords: :

• Brownian motion
• swarm
• cooperative
• social insects
• simulation
• model
• emergent

Introduction

Cooperative behavior is a hallmark of living organisms across many length-scales, from colonies of bacteria to schools of fish.¹ Understanding how such behavior is coordinated has important consequences for biological phenomena such as growth and cancer, which result from orchestrated communication between cells. Cooperative behavior also has applications in robotic self-assembly, the development of autonomous, self-propelled interacting agents that link together to perform complex tasks without centralized command.^2-4 Shrinking technologies are enabling robots to act more autonomously and in a more life-like manner, making visions of modular robotics a reality. For both biological and robotic applications, the ability to numerically scale up a swarm from 10 to 10,000 individuals is an important trait. However, observing such phenomena in nature and quantifying the algorithms involved are rare. In this combined experimental and theoretical study, we investigate the behaviors underlying the coordination of large swarms of fire ants.

Certain cooperative organisms can link their bodies together to build large living networks called self-aggregations. This behavior can increase a colony’s structural integrity in the face of harsh environments. For example, bacteria constructs biofilms by excreting scaffolding in the form of extracellular polymeric substances, enabling them to survive disinfectants. Another class of self-aggregations comprises those built by social insects.⁵ Bees, army ants, and fire ants are known to readily construct self-aggregations such as bridges to cross ravines, bivouacs to provide shelter during nomadic travels, and rafts to float upon during flash flooding. Although these structures have been documented in the biology literature, little is known quantitatively about their construction process.

A recent study by the authors has provided some insight on the mechanisms underlying raft construction.⁶ In that study, we constructed spherical clumps of ants and floated them on the water surface. We observed that ants would morph their raft into a pancake shape of 2–3 ant layers in thickness, as shown in Figure 1. We predicted the spreading rate of this pancake by tracking ant walking patterns to formulate a differential equation in terms of the number of ants n on the bottom layer of the raft. The current study represents two improvements to this model.

Figure 1. A sphere of ants will spread out to a pancake in a matter of minutes. Mobile ants on the top layer walk toward the edge and become part of the fixed bottom layers. This leaves a new mobile layer of ants that follow the same pattern. This behavior continues until the raft reaches an equilibrium thickness of 2.5 ants.

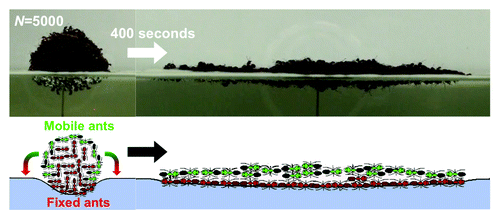
One motivation for the current study is the absence of analysis or explanation of the overall shape of the raft, which had been circular in our previous experiments. In fact our previously published analysis implicitly assumed circularity but gave no explanation to how it arises. A second motivation is our observation that our model was a better fit for small rafts of 1,000–6,000 ants than for large rafts greater than 8,000 ants. Fire ant rafts found in nature often comprise entire colonies of ants, and thus can span tens of centimeters and carry tens of thousands of ants, as shown in Figure 2A. In order to build a model that can better account for the largest of rafts, we have re-investigated the growth of ant rafts, focusing on those of large size.

Figure 2. Ant rafts (A-B) and a Styrofoam raft (C) for measuring ant trajectories. In (B-C), the lines show sample ant trajectories interrupted by the dots indicating turns made by the ant.

In this study, we report the results of a model specifically for large ant rafts. We begin in the next section by reviewing our previously published work. We follow with our new experimental results for the trajectories of ants atop large rafts and discuss the resulting implications to our model. We also include a justification for the circular shape of the ant raft. We continue with a mathematical modification to our model from 2011 and compare its predicted results to those of our previous model. Next, in Discussion, we flesh out the implications of our work and suggest directions for future research. Lastly, in Methods, we provide details of our experimental procedures.

Results

We begin by reviewing results from our previous model. Then we discuss measurements of a new parameter, the step size, which we incorporate into this previous model. Next we reformulate our model using this new parameter. After that we present results comparing the utility of this new model to its predecessor. An assumption in this modeling is that rafts are perfectly circular. Lastly, we proceed to report measurements and simulations of the shape of rafts to justify this assumption.

Review of previous model

We find that when a sphere-shaped clump of ants is placed on the water’s surface, it quickly morphs into a pancake-like shape, as shown in Figure 1. Ants rearrange themselves by traveling atop the raft (shown in green) and joining to its edges, becoming part of the stationary bottom layer of ants (shown in red). This motion consequently exposes a new layer of ants that become mobile and travel atop the previously mobile but now stationary ants. This new layer of ants also travels toward the newly created edge, and the process repeats until the raft has shortened to a height h of 2.5 ± 0.1 layers.

We also made the raft thinner than h by plucking ants off the top. We observed that the radius of the thinned raft decreased as ants on the edge moved back to the top. There were insufficiently many ants on the top to keep the ants on the edge pinned by walking on top of them. Consequently the raft will begin to shrink as ants on the edge move back to the top.

The rate that the ant rafts morph is a function of how quickly the ants can reach the raft edge. We observed ants moving on small ant rafts, composed of N = 1,000 ants. Figure 2B shows an actual example trajectory of a single ant in the raft. As shown, during the growth phase of the raft, the ant moves in straight-line randomly-directed paths alternating with ricochets off the raft edge with probability 1 − p, and stops when it joins the bottom layer at the edge of the raft. An important aspect of this motion is that the ants do not change direction appreciably until they reach the raft edge.

Using locally gathered experimental parameters describing ant behavior and average ant trajectories on a growing disc, we formulated the following expression for the number dn/dt of ants added to the bottom layer per second:

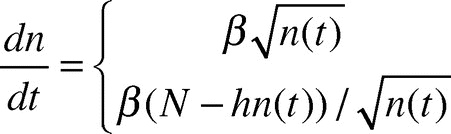
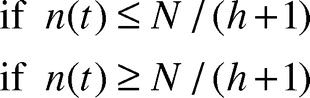
Our previous model involved a number of parameters measured experimentally, which we reiterate here. The initial condition for the equation (1) can be found using N, the total number of ants forming the raft, which sets the number of ants on the bottom when the ant raft is initially shaped as a sphere. The local parameters include the following: h = 2.5, the eventual thickness of raft in terms of number of ants; α = 3.1, the average number of circle radii traveled by a straight-line motion ant until sticking to a circle boundary; γ = 34, the ant density in an ant layer in units of ants per cm²; v = 0.39, the instantaneous speed of an ant’s straight motion in cm/sec; and the fraction. We use the following expression for converting raft radius to an equivalent number of ants on the bottom layer: where the radius of raft at time t is in cm. The expression “≥ N/(h + 1)” indicates the raft reaches a point in its growth where there is a full layer of ants or less on top of the raft available to add to the edges. The inverse inequality indicates a full layer of ants or more are available to add to the edges. For a complete derivation of Eq.(1), we refer the reader to our previous work.⁶

Step size measurement

For modeling, we have approximated the motion of individual ants using two protocols. As reviewed in the previous section, we observed ant motion atop rafts of ants. We now observe single ants atop Styrofoam discs of the same size as the rafts, approximately 4 cm. We choose the white Styrofoam to avoid the problem of visually resolving a small ant atop a large raft of live ants. We find no qualitative differences between locomotion on the two surfaces. This similarity is consistent with observations by Fourcassie, who finds there is no significant difference in trajectory characteristics between solitary ants and groups of ants, although there are velocity differences.⁷

Conducting experiments on a larger Styrofoam disc (r > 4 cm), we find that the ant trajectories vary from those on small disks (r < 4 cm). On this larger disk, ants walk in straight-line segments of length s, interspersed by turns in a random direction, as shown in Figure 2C. In our modeling section we refer to this distance s as the step size. Using a sample size of m = 14 random turns by one ant, we find s to be 4 ± 1.5 cm.

Although ants make a greater number of turns on larger rafts, we observed that their instantaneous walking speed remains the same as on small rafts. The average walking speed along the straight-line paths is v ≈0.39 cm/s. The speeds on large rafts match our previously measured speeds on small rafts,⁶ as well as measurements of ant speed made by Gordon.⁸

Based on our combined observations of motion on both small rafts (see previous section) and large ant rafts, we hypothesize the following algorithm for individual behaviors during raft construction:

1. An ant only moves if there are no ants atop it.

2. When an ant moves, it travels straight in a random direction (uniformly distributed over 360 degrees) for a distance s, changes direction randomly, and repeats this pattern until it reaches an edge.

3. Upon reaching an edge, an ant gets stuck with probability p ≈0.3, measured experimentally. With complementary probability 1 − p, the ant ”bounces” off the edge and begins traveling straight in a random direction away from the edge (uniformly distributed over 180 degrees), continuing with behavior 2.

Ants follow the algorithm above until they are pinned at the edge of the raft by other ants. The modification from the previous algorithm reviewed in the previous section is the inclusion of a step size s.

Diffusive model

For the purpose of modeling raft spreading behavior, we idealize a single ant’s behavior as choosing a new random direction after traveling a step size s. This behavior is consistent with our previous observations: if the radius r of the raft is less than s, then one would simply observe ants traveling in a straight line until reaching an edge, as was the case of our previous observations. At the other extreme, when r is very large compared with s, this behavior will, in the limit, approach Brownian motion.

We had observed previously⁶ how clumps of ants behave as a viscoelastic solid as the raft flows from an initially spherical shape to form a pancake. Their diffusive motion is consistent with this view of ants as a fluid. Using the measured step size s and walking speed v, we can roughly estimate a diffusion coefficient D for ants, given by vs, to be 1.6 cm²/s. For some comparison, D is largest in gases (10³ cm²/s), intermediate in liquids (0.01 cm²/s), and smallest in solids (10⁻⁷ cm²/s). This hierarchy is due to the kinetic energy of the respective phases and their inter-atomic spacing. Larger values of D mean the molecules spread out at higher rates. Our diffusion coefficient for rafting ants falls in between those of gases and liquids.

In Brownian motion,⁹ the expected time to reach the boundary of a disc of radius r from the center is proportional to r². The effective velocity u of an ant is therefore proportional to . The effective velocity also ought to be proportional to the instantaneous velocity v, by scaling reasoning. Moreover, the effective velocity ought to be proportional to the step size s, again by scaling reasoning. This is because if one took k steps of size s, then irrespective the direction each step is taken, one would end up exactly s times as far away as if one had taken the same k steps of size 1. Hence the effective velocity of an ant, when r is large, should be . Combining these two cases, we may write the ant’s effective velocity u as a function of the raft size:

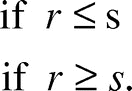
Note that the effective velocity u(r) is a continuous function of r and is consistent with ant- trajectory observations in both Figure 2B and C.

The formula for the ant’s effective velocity is also at least fairly accurate for intermediate values of r. Approximate the circle as a square, and ant motion as random vertical and horizontal steps of length s. The expected number of horizontal steps to reach a boundary equals the expected number of steps a simple one-dimensional random walk takes to get steps to the left or right of its starting location,¹⁰ which is well known to equal . The total time for the horizontal motion to reach a boundary is therefore . Hence the effective speed is . Vertical motion behaves identically. Neglecting constant factors, the effective speed is again , as found previously.

Using this effective speed given in Eq.(2), we re-formulate Eq.(1) to include two new regimes dictated by the value of raft radius r(t) relative to s. We refer to this new model as the “diffusive model.” Our modified differential equation to predict the rate of growth of the ant raft is defined in terms of the four regimes (A-D) that follow:

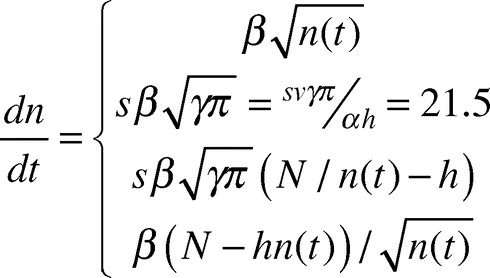
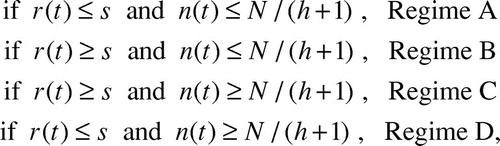
where n(t) is the number of ants on the bottom surface of the raft and t is in seconds, and s is our new parameter ant step size. The new model differs from Eq.(1) by the inclusion of two new regimes that are dictated by the value of r(t) relative to s. When r ≤ s, the model is equivalent to Eq.(1) and follows either Regime A or D depending on the how many ants are on the bottom. Regimes B and C are activated when the raft grows to a radius r ≥ s, at which point instantaneous velocity v is replaced with effective velocity u = vs/r.

Comparison to previous model

We use a first-order scheme to numerically integrate our governing equation for dn/dt given in Eq.(3), incorporating the effective velocity given in Eq.(2). In this section we report results of this new diffusive model to our previous straight-path model.

Previously,⁶ we limited N to 10,000 ants. We now present new results for experiments with larger ant rafts of N = 15,000 and 22,500. Figure 3A-D shows the time course of the number of ants n on the bottom of the raft for various sizes of raft as indicated. Experiments are denoted by the open symbols, and associated predictions from theory are given by the solid line (diffusive model) and dashed line (straight-path model). Both models are a good fit for short times (t ≤ 50 sec) when r is small, as expected. For instance, for the intermediate-sized raft of n = 6,000 ants in Figure 3A, the results for both models are nearly indistinguishable. This is because these rafts are small enough (r ≈s) that the diffusive behavior in Eq.(2) doesn’t take effect until the raft is almost complete.

Figure 3. The growth of ant rafts N = 6000, 10000, 15000, and 22500. The vertical axis is n(t), the number of ant on the bottom layer. The floating ant ball spreads out on the water’s surface and reaches an equilibrium size. The plots compare experimental findings to both our previous straight-path only model and our new model that incorporates a Brownian element, accounting for the diffusive nature of ant motion. The diffusive element is triggered when the radius of the raft reaches a critical size. For large N, the diffusive model is clearly a better fit than the straight-path only model.

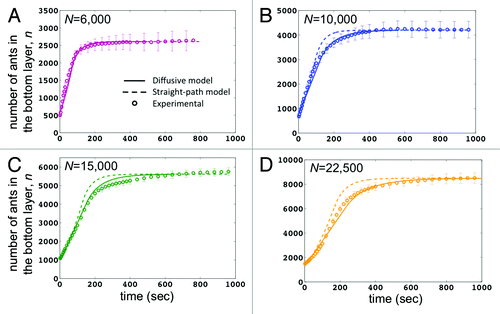
For larger N, the discrepancy between the models is more apparent, with the diffusive model providing a better fit for the experimental results (Fig. 3A-D). The raft of size N = 22,500 ants (Fig. 3D) is a good example of a clear deviation between the two models. While our previous model failed to accurately predict the growth rates for very large rafts, our new results show that the diffusive element of our new model accurately captures the dynamics of the larger raft. Specifically, the straight-path model over-predicts the construction rate in Figure 3D, as shown by the higher rate of growth between 100–250 sec. In contrast, the diffusive model shows a raft growth rate that is slower and more consistent with the experiments. This difference occurs because the new model increases the time for the ants to reach the edge of the raft.

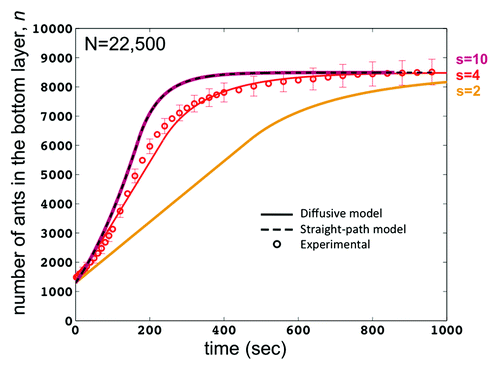
By using a range of values for the step size s in our diffusive model, we find that the raft growth rate is highly sensitive to step size. Figure 4 shows the time course of the number of ants on the bottom of the raft for a series of values of s = 2, 4, and 10 cm. As s approaches the final raft radius (the solid purple line signifying s = 10), the diffusive model approaches the straight-path model (the dashed black line). A large step size means that the ants do not change direction until reaching the raft’s edge, thus exhibiting the same behavior as in our straight-path model. Also, as s approaches zero (solid orange line signifying s = 2), the ant behavior becomes purely diffusive and raft construction time approaches infinity. Cases s = 2 and s = 10 shown in Figure 4 demonstrate the high sensitivity of the model to step size, highlighting the importance of measuring step size accurately. The s value of 4 cm found in our experiments (solid red line) yields diffusive model results that match closely to our experimental results (red circles).

Figure 4. Time course for the number n of ants on the raft bottom for a raft N = 10,000 ants. Solid lines are the diffusive model for various values of ant step size s. The plot for s = 10 is consistent with the straight-path (dashed line) model since an ant won’t change direction before reaching an edge. The value s = 2 shows longer construction times for the raft since the ants must make many direction changes before reaching an edge. The value s = 4, found experimentally, yields model results that are consistent with our experimental findings and are also clearly a better fit than the straight-path only model.

We now comment on the significance of the four regimes given in Eq.(3). We use as an example the model predictions given by the red solid line in Figure 4, the diffusive model with s = 4. Here, Regime A is the same as the original model, but it only lasts while the raft radius r(t) is less than the step size s, or For very large rafts, N > 35,000 ants, Regime A does not occur at all because the initial sphere of ants is so large that . In Figure 4, Regime A occurs during time 0 to approximately 40 sec. Regime B has linear growth of n(t). This can be seen in Figure 4 in the time interval approximately [40, 105] seconds, where the experimental data fits this linear growth very well. During Regime C, n(t) grows at a decreasing rate, approaching a growth rate of 0 as n(t) approaches N/h. Regime D does not occur at all unless ants, which is impossible for ants. Since n(t) never exceeds N/h = N/2.5 (i.e., 2.5n(t) ≤ N) and the new model doesn’t take effect unless n(t) > 1,710 ants, the new model never takes effect unless N > 2.5(1,710) ≈4,300 ants.

In summary, for N ≤ 4,300 our new model behaves exactly like the straight-path model of our previous paper, transitioning directly from Regime A to Regime D, where the four regimes are listed in Eq.(3). For 35,000 ≥ N ≥ 6,000 our new model behaves like Regime A, as in the straight-path model, for a short time period, and then progresses to the linear growth of Regime B, ending with Regime C. For N > 35,000 our new model begins immediately with the linear growth of Regime B, ending with Regime C. For the narrow range 4,300 ≤ N ≤ 6,000 our new model progresses from Regime A to Regime D to Regime C.

In our derivation of the regimes of validity, we use an approximation that does not appear to affect the accuracy of our model substantially (as shown in Fig. 4), but is worth noting here. Although Regimes B and C don’t kick in until r ≥ s, it is more complicated than a simple switch at r = s. Instead it is a gradual shift between regimes. The point at which r = s is roughly in the middle of the shift. The beginning of the shift is at 2r = s, which is the smallest diameter at which the ant might change direction, but occurs zero percent of the time. As r increases and approaches s the probability of random direction changes will increase. At r = s, a direction change occurs 2/3 of the time after bouncing off a boundary, but less than 1/2 and more than 1/3 of the time when starting at a random point on the raft surface, yielding slightly more than a 1/2 probability that an ant will change direction. Therefore, r ≫ s marks the end of the shift, but even when r ≫ s, there will still be a few short moves that hit a boundary before the travel distance reaches s.

Raft circularity

It has been established¹¹ that when N random elements starting at the origin of a two-dimensional grid each in turn performs a simple random walk until reaching an unoccupied site, the set of occupied sites will form a disc whose circularity approaches perfection with probability 1 as N approaches ∞. The behavior of ants on large rafts can be idealized in this manner for analyzing the raft’s shape. We expect that as the number of ants in the raft N increases, the equilibrium profile shape will become more circular. To measure the raft’s deviation from circular, top view images of rafts (size N = 5, 10, 50, 100, 1000, 5000, and 10000) at equilibrium (Fig. 5A) are processed using Matlab to find an ellipse which best fits the raft profile. We define eccentricity of the ellipse as e = 1 − min/maj, where min and maj are the lengths of the minor and major axes of the ellipse respectively. An e value of 0 indicates a perfect circle where min = maj. The e values for the raft profiles are plotted against logN revealing a declining trend in e as expected (Fig. 5C). These results show that the raft is indeed nearly circular and approaches that limit as N approaches infinity.

Figure 5. (A) Selection of raft profiles at equilibrium. (B) Sample profiles from our simulation that randomly adds individuals to the edges. (C) Plot comparing the eccentricities for experimental rafts and average values of simulation data.

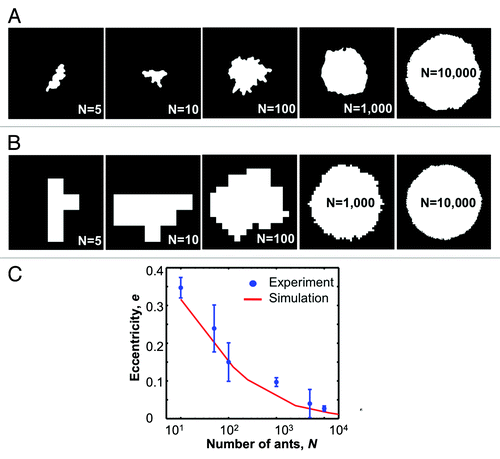
Asymptotic formulae for circularity are known,¹¹ but to compare actual ant raft shapes to the random walk growth model around an origin for moderate values of N, it is necessary to run our own simulation. A single 1x1 element rests at an origin (0,0). Each iteration, another element starts at the origin and follows a random walk of unit steps until it reaches an unoccupied site. For the first element added, this would be either (1,0), (0,1), (-1,0), or (0,-1). The second element to be added then starts at the origin and performs the random walk on this new two-element shape. This continues until the number of elements reaches N. We ran this simulation 20 times each for N = 10, 50, 100, 1000, 5000, and 10000. Select images of the resulting shapes are shown in Figure 5B. Figure 5C plots the average eccentricity value against logN. Before plotting, values of N from 50 through 10,000 for the simulation were multiplied by 2.5 for comparison to our experimental findings. This was done because all elements in a simulation form a single layer, but real ants form a raft 2.5 layers thick. This means that a simulation of N elements corresponds to a raft of 2.5N real ants. In our simulations, the value N = 10 was not multiplied by 2.5 because, in our experiments, a raft of only 10 ants forms a single layer.

The simulation follows the experimental data very closely. The closeness of this fit supports our hypothesis that the individual ant random movements cause the circular shape of the ant raft. If circularity were due to some other cause, it seems unlikely that the relationship between raft size and raft circularity would be the same.

Discussion

The two main contributions of this work are the following: (1) We improve the accuracy of our previous model’s assumptions of individual behavior, and thereby improve the accuracy of the model’s predictions for larger rafts without sacrificing accuracy for smaller ones. We verify this improvement through a comparison to new data gathered from observing large rafts, the results of which clearly show the new model’s improvement. (2) Through describing the behavior of an individual ant within the raft with a few simple rules, we show that ants can build circular rafts despite the inability of individuals to perceive the overall shape of the raft. Our numerical simulation of this phenomenon predicts a pattern of greater circularity as the raft size increases, a pattern that closely matches our experimental data.

Our earlier model of rafting fire ant motion⁶ described their individual behavior as strictly straight-line motion combined with a bounce probability function to describe raft edge conditions. Our current model uses a Brownian element based on new observations of the step size s of ants moving diffusively on large rafts. Using an s value from experiments yields construction times in the model that more accurately reflect those found in experiments. We have also presented the time-regimes of validity of our new model in Eq.(3), which are based on the initial size of the raft with respect to s.

Our previous model also made an implicit assumption of raft circularity. Our new simulations based on a random walk from an origin provide an explanation for the circular raft shapes we observe. The close fit between the shape simulations and the actual raft shape supports the validity of our explanation.

Incorporating a Brownian element is more in line with previous work on animal behavior. In previous literature, diffusion models have shown broad applicability to modeling animal motions such as the swarming behavior of insects. Specifically Harkness developed a model that incorporates both straight-line and diffusive elements to describe the foraging behavior of ants.¹² Others such as Schweitzer and Theraulaz both suggest a diffusive mechanism behind the ant’s walking patterns.^13,14 Helland discusses the effectiveness of diffusion models for the dispersion of insect populations attracted toward a point.¹⁵ Such diffusive behaviors are especially important when the number of agents, be they ants or robots, is very large, as in the case of ant rafts, which can exceed 100,000.

We have observed fire ants in a raft moving in random directions interspersed by a distance s. Rather than systematic searching, ants typically employ random search strategies.¹⁶ This allows moving to be optimized so as to increase their chances of locating resources by increasing the chances of covering certain regions. The optimal solution often arises by merely carrying out a random-walk search strategy.¹⁶ In the case of rafting, the step size may be a behavior originally adapted for moving on land.

The diffusive behavior observed sheds light on Detrain’s claim that ants are not simply ”behaving like molecules,” but rather are acting upon the complex and changing parameters of their surroundings based on response thresholds.¹⁷ Studies have shown that ants can collectively “make decisions,” demonstrating capabilities far beyond simple molecules.^18,19 Conversely, our research reveals that when ants form self-assemblages, such as the floating raft, they begin to exhibit behavior similar to the diffusive nature of some molecules. Moreover, a short set of behavior rules is sufficient to predict their group motion. These results suggest that in times of emergency, such as rapid raft construction, ants do in fact behave like molecules to some extent.

There are a number of other factors that likely could have an effect on rafting dynamics. Chemical signals have been shown to affect a colony’s exploration of new space through recruitment.⁸ The rate of antennal contact is a way for ants to measure raft-mate density.²⁰ The presence of queen and brood in a raft, such as occurs in nature, affects the worker distribution of ants within a raft. A heightened defensiveness while rafting will cause behavioral changes in the ants.²¹

The above factors, as well as the position of ambient lights, may affect raft equilibrium shape in natural settings. Also, a floating or partially submerged object such as grass or twigs (as in Fig. 2A) appears to strongly affect the shape of the portion of the raft adjacent to the object. We also have observed the raft forming “appendages” that seem to be reaching out toward nearby landmasses as an attempt to dock the raft.

The model we have presented omits these factors. In particular, it omits chemical signaling and antennal contact, which occur in both natural and laboratory settings. Yet, it provides an accurate representation of the growth rate and shape of large and small ant rafts in laboratory settings. This suggests that we have identified the critical elements of the individual ant behaviors that result in the observed raft formation.

Methods

Ant husbandry

Ant colonies are procured from roadsides near Atlanta, GA. Colony selection aims for an average ant weight of 1.5 mg. Colonies are removed from the soil and placed into bins according to methods by Chen.²² Ants are fed crickets and water three times a week. They are housed in an 8-h light and 16-h dark cycle. As a measure taken to ensure repeatable results, ants that are used for experimentation are afterward reintroduced to the colony and allowed at least 2 h to resume normal colony behavior before being used again.

Filming of large ant rafts

Using high-definition video cameras, we film the construction of ant rafts floating on the water surface. We parameterize the raft size by the number of ants in the raft N, and perform experiments on rafts of N = 6000, 10000, 15000, and 22500, measured by weighing the rafts. Ants are initially collected from bins and placed into a beaker, taking care to avoid collection of queens and males. The beaker is then swirled so that ants clump together forming a cohesive spherical aggregation. To ensure a spherical aggregation, beaker size is chosen such that when the ants are formed into a ball and centered in the beaker, there is at least a 1-cm and no more than a 2-cm gap between the ball edge and beaker wall. Using tweezers, ant balls are placed on the surface of clean, room-temperature water, and centered upon a partially submerged pin to prevent drifting. Resulting ant motion is recorded from above until equilibrium is reached. Four trials for each raft size N are performed and filmed. The average top-view projected-area change of the ant raft in number of ants is digitized using image processing for each N.

By tracking individual ants as we played videos frame-by-frame, we determined values for several parameters in the model. These parameters include the average walking speed v, the probability p of joining the bottom layer during the growth phase, the walking distance s between turns, and ant planar density γ in ants per centimeter squared. The use of these experimental findings in our model development is documented in our previous work.⁶

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgments

The authors thank the National Science Foundation for support (IOS-0920402).