Figures & data
Figure 1. For each triangle T ∈ 𝒯, there is one fixed reference edge, indicated by the double line (left, top). Refinement of T is done by bisecting the reference edge, where its midpoint becomes a new node. The reference edges of the son triangles are opposite to this newest vertex (left, bottom). To avoid hanging nodes, one proceeds as follows: we assume that certain edges of T, but at least the reference edge, are marked for refinement (top). Using iterated newest vertex bisection, the element is then split into 2, 3 or 4 son triangles (bottom).
Figure 2. Refinement of an element A by one (a), two (b) or three (c) bisections and notation used in the proof of Lemma 3.3.
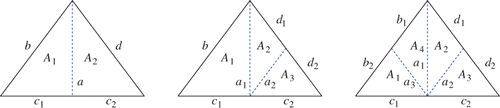
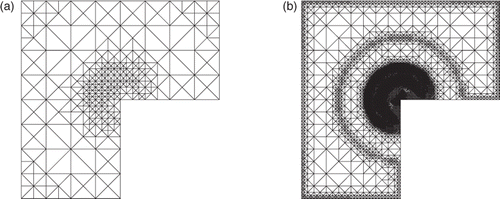
Figure 3. The element A ∈ 𝒯ℓ is refined by two bisections. It has two neighbouring elements B, D ∈ 𝒯ℓ, whereas the third edge is on the boundary.
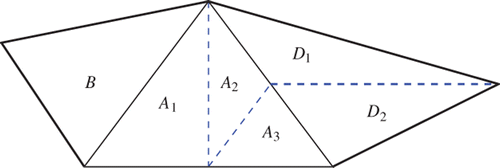
Figure 4. Numerical results for uniform and adaptive mesh-refinement with θ = 0.6, where ϵℓ = 𝒥(U ℓ) − 𝒥(u), ηℓ and oscℓ are plotted over the number N = #𝒯ℓ of elements.
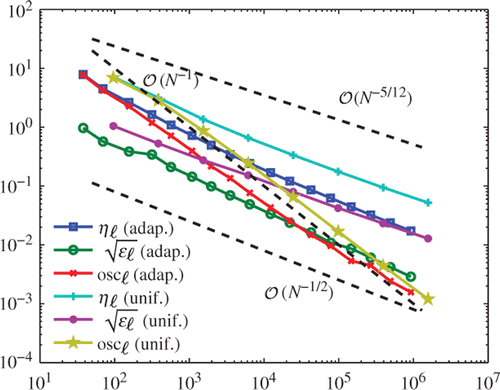
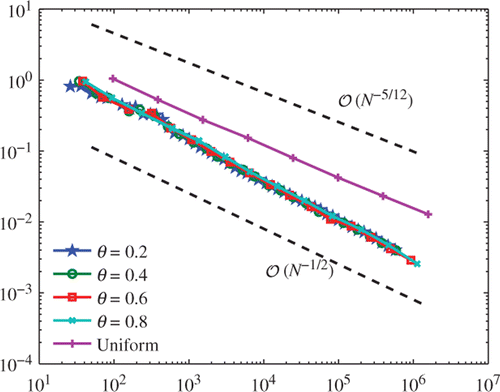
Figure 5. Numerical results for for uniform and adaptive mesh-refinement with θ ∈ {0.2, 0.4, 0.6, 0.8}, plotted over the number N = #𝒯ℓ of elements.
Figure 6. Adaptively generated meshes 𝒯5 (a) and 𝒯11 (b) with N = 568 and N = 22140 elements, respectively, for θ = 0.6.
Figure 7. Galerkin solution U 8 on adaptively generated mesh 𝒯8 with N = 3524 elements for θ = 0.6.
