Trusting: Alone and together

Figures & data

Table 1. Modelling decisions in selected social network learning literature.

Paper	Rationality	Communication	Signals
Bala & Goyal (1998)	myopic	actions and signals	conditional
Molavi et al., (2018)	imperfect-recall	belief	independent
Harel et al., (2021)	myopic	actions	independent
Huang et al., (2021)	non-myopic	actions	independent

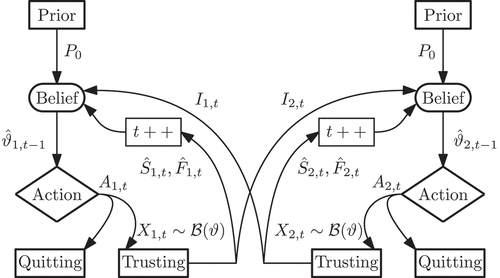
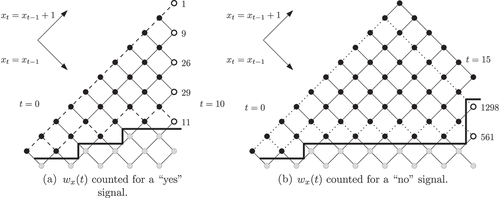
Figure 1. (a) the single agent learner model illustrated conceptually and (b) two example paths of the model dynamics in the random walk interpretation. $\mathcal{B}(\mathit{\vartheta })$ denoting the Bernoulli distribution with parameter $\mathit{\vartheta }$.

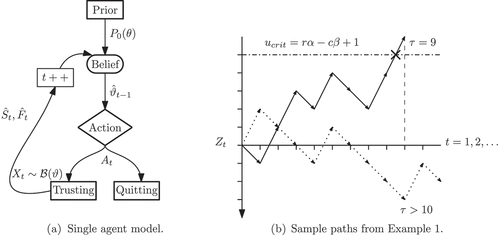
Table 2. Sample paths and agent beliefs as random walks.

(A) Solid line in Figure 1(b).
$\mathit{t}$	0	1	2	3	4	5	6	7	8	9
${\hat{S}}_{\mathit{t}}$	0	1	1	1	2	2	3	4	4	4
$Z_t$	0	−1	1	3	2	4	3	2	4	6
${\hat{\vartheta }}_{\mathit{t}}$	0.8	0.82	0.75	0.69	0.71	0.67	0.69	0.71	0.67	0.63
(B) Dotted line in Figure 1b.
$\mathit{t}$	0	1	2	3	4	5	6	7	8	9	10	11
${\hat{S}}_{\mathit{t}}$	0	0	1	2	3	3	4	5	6	7	7	8
$Z_t$	0	2	1	0	−1	1	0	−1	−2	−3	−1	−2
${\hat{\vartheta }}_{\mathit{t}}$	0.8	0.73	0.75	0.77	0.79	0.73	0.75	0.76	0.78	0.79	0.75	0.76

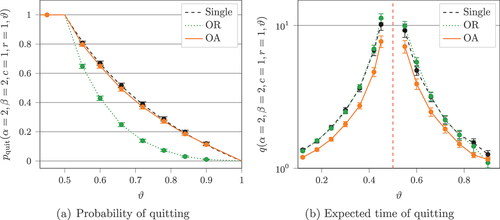
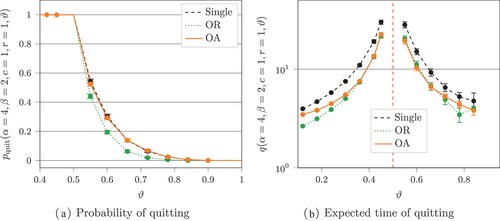
Figure 2. The probability of a single agent quitting $p_{\mathrm{quit}}(\mathit{\alpha },\mathit{\beta },\mathit{c},\mathit{r},\mathit{\vartheta })$ plotted against $\mathit{\vartheta }$ for different values of $\mathit{r}$ while $\mathit{\alpha }=\mathit{\beta }=2$ and $\mathit{c}=1$. Analytical results are plotted as lines, while simulated results (4 000 iterations) are shown as points with 95% confidence intervals.

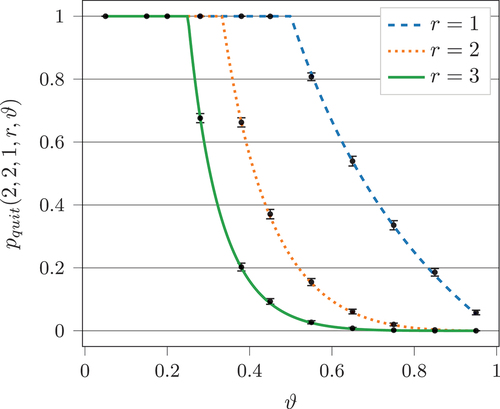
Figure 3. Expected time in the system conditioned on the agent quitting at some $\mathit{t}<\mathrm{\infty }$ plotted against $\mathit{\vartheta }$ for different values of $\mathit{r}$ while $\mathit{\alpha }=\mathit{\beta }=2$ and $\mathit{c}=1$ on a log-linear axis. Analytical results are plotted as lines, while simulated results are shown as points with 95% confidence intervals.

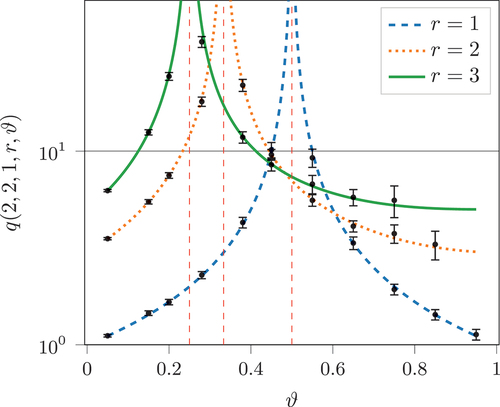
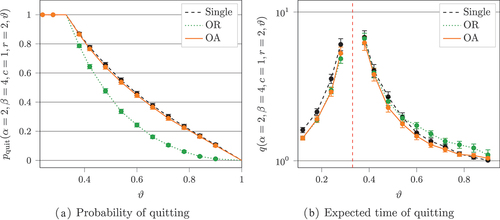
Figure 4. The probability of a single agent quitting plotted against $\mathit{\vartheta }$ for different values of $\mathit{c}$ while $\mathit{\alpha }=3,\mathit{\beta }=1$ and $\mathit{r}=1$. Analytical results are plotted as lines, while simulated results (4 000 iterations) are shown as points with 95% confidence intervals.

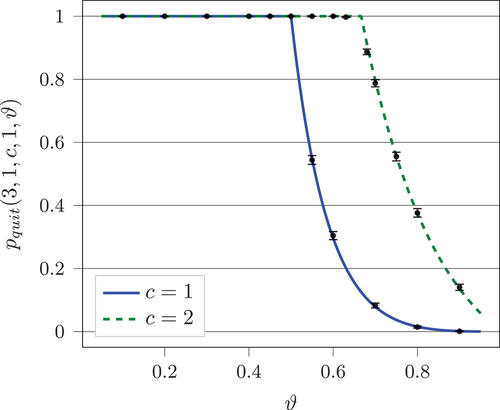
Figure 5. Expected time in the system conditioned on the agent quitting at some $\mathit{t}<\mathrm{\infty }$ plotted against $\mathit{\vartheta }$ for different values of $\mathit{c}$ while $\mathit{\alpha }=3,\mathit{\beta }=1$ and $\mathit{r}=1$. Analytical results are plotted as lines, while simulated results are shown as points with 95% confidence intervals.

Figure 6. The observable rewards model of learning.

Figure 7. The observable actions model of learning.

Figure 8. An illustration of the weighting $w_x(\mathit{t})$ used in the interpretation of the observed action.

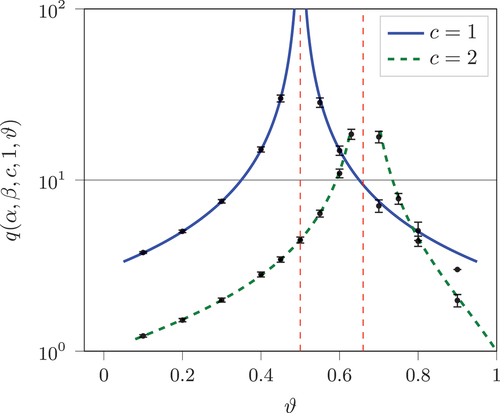
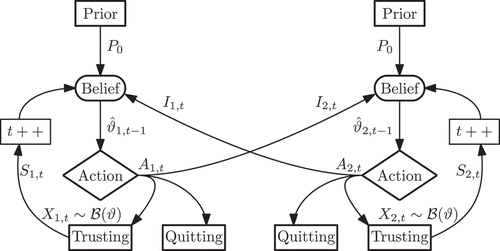
Figure 9. The random walk interpretation of the or model as well the individual sample paths of the respective agents.

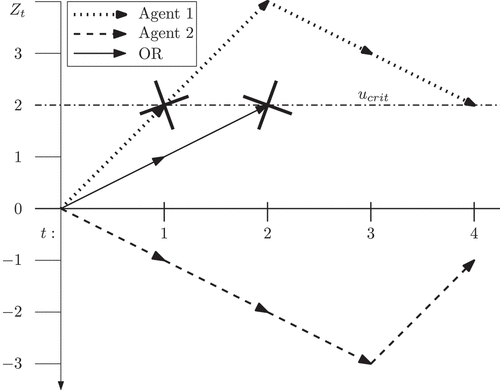
Table 3. Estimates, ${\hat{\vartheta }}_{\mathit{t}}$ in the respective models.

$\mathit{t}$	Agent 1	Agent 2	OR (1)	OR (2)	OA (1)	OA (2)
0	0.714	0.714	0.714	0.714	0.714	0.714
1	0.625	0.750	0.667	0.667	0.625	0.750
2		0.778	0.636	0.636		0.700
3		0.800				0.727
4		0.727				0.667

Figure 10. Simulation results for $\mathit{c}=\mathit{r}=1$ in the $u^{\ast }=1$ case.

Figure 11. Simulation results for $\mathit{c}=\mathit{r}=1$ in the $u^{\ast }=3$ case.

Figure 12. Simulation results for $\mathit{c}=1$ and $\mathit{r}=2$ in the $u^{\ast }=1$ case.

Figure 13. Simulation results for $\mathit{c}=1$ and $\mathit{r}=2$ in the $u^{\ast }=3$ case.

Figure 14. Simulation results for $\mathit{c}=2$ and $\mathit{r}=1$ in the $u^{\ast }=1$ case.

Figure 15. Simulation results for $\mathit{c}=2$ and $\mathit{r}=1$ in the $u^{\ast }=3$ case.

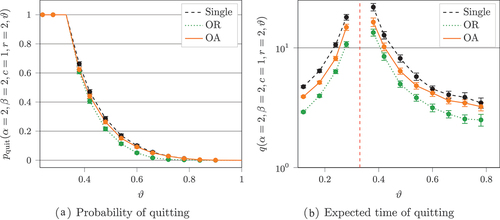
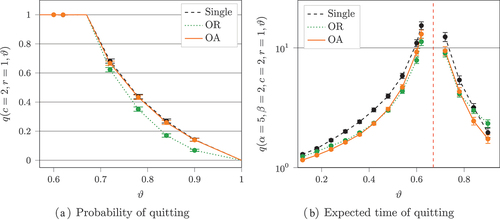
Figure 16. The results of extra simulation runs for the probability of quitting. In these runs $\mathit{c}=3$, $\mathit{r}=2$, and $u^{\ast }=2$.

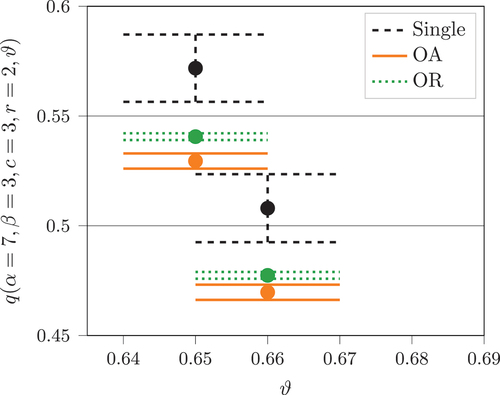
Table 4. Two random walks.

Walk	Step $+$	$\mathbb{P}(+)$	Step $-$	$\mathbb{P}(-)$
$Z_G$	$\mathit{c}$	$1-\mathit{\vartheta }$	1	$\mathit{\vartheta }$
$B_G$	1	$\mathit{\vartheta }$	$\mathit{c}$	$1-\mathit{\vartheta }$

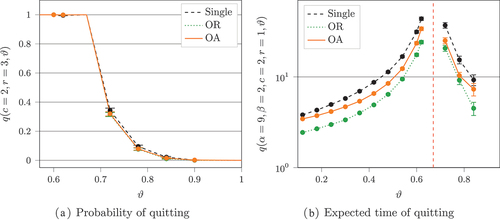
Table 5. Probability of quitting and the expected time to quitting in the single agent model (Sol), the observable actions model (OA) and the observable rewards model (OR). Parameters $\mathit{\alpha }$ and $\mathit{\beta }$ set such that $u^{\ast }=1$

(A) Probability of quitting
$\mathit{c}=\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.30	0.36	0.42	0.45	0.55	0.60	0.66	0.72	0.78	0.84	0.90
Sol	1.0	1.0	1.0	1.0	1.0	1.000	0.808	0.669	0.518	0.390	0.288	0.198	0.119
OA	1.0	1.0	1.0	1.0	1.0	0.999	0.797	0.649	0.493	0.370	0.272	0.186	0.113
OR	1.0	1.0	1.0	1.0	1.0	1.000	0.648	0.429	0.248	0.138	0.072	0.030	0.010
$\mathit{c}<\mathit{r}$:
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{3}$						$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{4}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	0.832	0.755	0.611	0.495	0.394	0.311	0.241	0.170	0.108
OA	1.0	1.0	1.0	1.0	0.825	0.734	0.592	0.483	0.382	0.296	0.230	0.165	0.102
OR	1.0	1.0	1.0	1.0	0.745	0.621	0.424	0.292	0.190	0.120	0.066	0.030	0.010
$\mathit{c}=\mathbf{1},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{4}$
$\mathit{\vartheta }$	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	0.869	0.777	0.658	0.551	0.459	0.377	0.302	0.234	0.169	0.108
OA	1.0	1.0	1.0	0.866	0.766	0.641	0.538	0.447	0.366	0.289	0.225	0.164	0.102
OR	1.0	1.0	1.0	0.787	0.644	0.478	0.336	0.243	0.162	0.105	0.060	0.028	0.010
$\mathit{c}>\mathit{r}$:
$\mathit{c}=\mathbf{3},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{4},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.743	0.703	0.487	0.330	0.215	0.124
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.721	0.682	0.475	0.318	0.205	0.120
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.657	0.600	0.333	0.168	0.066	0.024
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathbf{5},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.999	0.682	0.438	0.27	0.142
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.000	0.667	0.433	0.26	0.140
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.000	0.622	0.352	0.17	0.068
(B) Expected time to quit
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.30	0.36	0.42	0.45	0.55	0.60	0.66	0.72	0.78	0.84	0.90
Sol	1.550	1.928	2.546	3.640	6.702	10.154	9.236	4.841	3.159	2.184	1.713	1.510	1.252
OA	1.352	1.597	2.037	2.740	4.718	7.710	7.116	3.891	2.480	1.883	1.478	1.237	1.155
OR	1.562	1.905	2.482	3.701	6.852	11.253	9.882	5.529	3.193	2.177	1.710	1.426	1.095
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{3}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{4}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.897	2.711	4.408	9.158	8.613	5.552	3.033	2.136	1.619	1.388	1.262	1.089	1.007
OA	1.690	2.231	3.584	7.342	7.082	4.439	2.702	2.057	1.532	1.308	1.184	1.121	1.039
OR	1.668	2.197	3.329	7.241	7.834	4.925	2.882	2.096	1.855	1.583	1.397	1.339	1.095
$\mathit{c}=\mathbf{1},\mathit{r}=\mathbf{2}$					$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{4}$
$\mathit{\vartheta }$	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	2.130	3.558	6.052	6.755	4.045	2.690	1.960	1.541	1.352	1.243	1.112	1.053	1.007
OA	1.898	2.904	5.278	6.204	3.804	2.277	1.770	1.463	1.282	1.192	1.102	1.084	1.039
OR	1.874	2.975	4.855	6.630	3.898	2.506	1.932	1.724	1.517	1.352	1.281	1.218	1.095
$\mathit{c}>\mathit{r}:$
$\mathit{c}=\mathbf{3},\mathit{r}=\mathbf{2}$					$\mathit{\alpha }=\mathbf{4},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	1.514	1.824	2.250	2.831	3.856	5.650	11.644	12.538	10.590	5.090	2.762	1.988	1.497
OA	1.328	1.531	1.833	2.242	2.941	4.552	10.004	9.398	7.988	4.010	2.388	1.750	1.418
OR	1.470	1.706	2.014	2.476	3.161	4.583	9.070	10.020	8.075	4.647	3.172	2.500	2.250
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{5},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	1.444	1.692	2.004	2.414	3.034	3.958	5.837	10.977	15.353	12.359	5.390	3.174	1.961
OA	1.270	1.418	1.627	1.891	2.332	3.072	4.684	9.232	13.028	9.437	4.308	2.448	1.734
OR	1.360	1.522	1.683	1.954	2.350	3.007	4.348	7.880	11.248	9.034	4.131	3.009	2.336

Table 6. Probability of quitting and the expected time to quitting in the single agent model (Sol), the observable actions model (OA) and the observable rewards model (OR). Parameters $\mathit{\alpha }$ and $\mathit{\beta }$ set such that $u^{\ast }=2$

(A) Probability of quitting
$\mathit{c}=\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.45	0.55	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.000	0.665	0.450	0.267	0.159	0.086	0.038	0.012
OA	1.0	1.0	1.0	1.0	1.0	0.999	0.647	0.429	0.252	0.141	0.078	0.034	0.012
OR	1.0	1.0	1.0	1.0	1.0	1.000	0.648	0.429	0.248	0.138	0.072	0.030	0.010
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{3}$						$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{3}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	0.700	0.574	0.376	0.249	0.160	0.101	0.060	0.028	0.011
OA	1.0	1.0	1.0	1.0	0.664	0.532	0.356	0.228	0.146	0.089	0.052	0.025	0.010
OR	1.0	1.0	1.0	1.0	0.659	0.526	0.328	0.204	0.124	0.082	0.048	0.022	0.010
$\mathit{c}=\mathbf{1},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{3}$
$\mathit{\vartheta }$	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	0.760	0.604	0.434	0.303	0.214	0.145	0.096	0.058	0.028	0.011
OA	1.0	1.0	1.0	0.747	0.589	0.418	0.297	0.204	0.136	0.086	0.051	0.025	0.010
OR	1.0	1.0	1.0	0.724	0.559	0.386	0.258	0.176	0.115	0.080	0.048	0.022	0.010
$\mathit{c}>\mathit{r}:$
$\mathit{c}=\mathbf{3},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{7},\mathit{\beta }=\mathbf{3}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.572	0.508	0.241	0.115	0.047	0.014
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.526	0.463	0.224	0.104	0.039	0.013
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.542	0.481	0.208	0.088	0.032	0.010
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathbf{7},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.998	0.482	0.202	0.078	0.022
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.999	0.466	0.197	0.072	0.021
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.000	0.441	0.164	0.048	0.013
(B) Expected time to quit
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.45	0.55	0.6	0.66	0.72	0.78	0.84	0.9
Sol	3.092	3.818	4.970	7.224	12.957	20.029	18.126	9.550	6.213	4.431	3.455	3.000	2.130
OA	2.615	3.077	3.863	5.228	9.552	15.800	14.165	7.130	4.683	3.664	3.172	2.597	2.362
OR	1.562	1.905	2.482	3.701	6.852	11.253	9.882	5.529	3.193	2.177	1.710	1.426	1.095
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	3.728	5.220	8.389	17.154	16.696	11.193	6.267	4.447	3.353	2.737	2.432	2.126	2.000
OA	3.060	4.100	6.736	14.250	13.397	7.572	5.232	3.762	2.888	2.511	2.203	2.148	2.026
OR	2.146	3.056	4.791	10.426	10.130	6.521	3.615	2.262	1.634	1.323	1.146	1.068	1.000
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	4.173	7.032	11.962	14.484	8.156	5.432	3.862	3.085	2.767	2.584	2.258	2.082	2.000
OA	3.364	5.240	9.371	11.275	6.624	4.143	3.223	2.668	2.415	2.311	2.138	2.091	2.026
OR	2.384	3.978	6.820	8.322	5.202	2.833	1.959	1.586	1.300	1.189	1.146	1.068	1.000
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	2.992	3.560	4.337	5.489	7.374	10.940	22.088	25.305	20.474	9.427	5.633	4.096	3.000
OA	2.559	2.906	3.429	4.159	5.572	8.398	17.574	16.967	14.051	7.563	4.701	3.219	2.755
OR	1.551	1.869	2.298	3.072	4.174	6.394	12.963	13.472	11.554	5.665	2.780	1.656	1.095
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{3},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	2.851	3.288	3.874	4.686	5.866	7.657	11.462	21.216	30.238	25.010	10.048	6.758	4.529
OA	2.467	2.712	3.087	3.552	4.325	5.639	8.380	16.212	23.482	16.732	7.119	4.745	3.602
OR	1.520	1.794	2.142	2.666	3.360	4.418	6.550	12.495	17.276	13.907	5.960	3.320	1.731

Table 7. Probability of quitting and expected time to quit in the single agent model (Sol), the observable actions model (OA) and the observable rewards model (OR). Parameters $\mathit{\alpha }$ and $\mathit{\beta }$ set such that $u^{\ast }=3$

(A) Expected time to quit
$\mathit{c}=\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathbf{4},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.45	0.55	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.000	0.544	0.304	0.138	0.063	0.025	0.006	0.001
OA	1.0	1.0	1.0	1.0	1.0	0.999	0.526	0.293	0.139	0.068	0.024	0.007	0.001
OR	1.0	1.0	1.0	1.0	1.0	1.000	0.441	0.194	0.062	0.019	0.006	0.000	0.000
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{3}$						$\mathit{\alpha }=\mathbf{5},\mathit{\beta }=\mathbf{5}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	0.999	0.594	0.436	0.238	0.128	0.066	0.033	0.013	0.004	0.001
OA	1.0	1.0	1.0	1.000	0.564	0.419	0.232	0.124	0.067	0.035	0.014	0.004	0.001
OR	1.0	1.0	1.0	1.000	0.546	0.386	0.186	0.084	0.030	0.012	0.005	0.000	0.000
$\mathit{c}=\mathbf{1},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	0.662	0.470	0.288	0.170	0.100	0.055	0.028	0.013	0.004	0.001
OA	1.0	1.0	1.0	0.622	0.441	0.264	0.152	0.092	0.051	0.028	0.012	0.004	0.001
OR	1.0	1.0	1.0	0.610	0.406	0.216	0.114	0.051	0.017	0.006	0.003	0.000	0.000
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathbf{3},\mathit{r}=\mathbf{2}$						$\mathit{\alpha }=\mathbf{7},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.439	0.367	0.129	0.040	0.011	0.001
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.396	0.317	0.116	0.036	0.008	0.001
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.404	0.334	0.100	0.025	0.004	0.000
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{1}$						$\mathit{\alpha }=\mathbf{7},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.996	0.344	0.096	0.022	0.002
OA	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.999	0.320	0.079	0.015	0.002
OR	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	0.999	0.315	0.076	0.011	0.000
(B) Expected time to quit
$\mathit{c}=\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{4},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.45	0.55	0.6	0.66	0.72	0.78	0.84	0.9
Sol	3.966	4.680	5.788	7.518	10.987	19.082	29.922	28.213	15.061	9.271	6.518	5.260	4.760
OA	3.463	3.834	4.468	5.503	7.552	13.513	22.291	19.470	10.387	6.623	5.273	4.385	3.815
OR	2.646	3.140	3.893	5.038	7.396	13.353	21.750	20.367	11.100	6.712	4.921	3.454	4.000
$\mathit{c}<\mathit{r}:$
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{3}$					$\mathit{\alpha }=\mathbf{5},\mathit{\beta }=\mathbf{5}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.35	0.45	0.48	0.54	0.6	0.66	0.72	0.78	0.84	0.9
Sol	4.487	5.678	7.859	12.435	24.902	26.330	16.966	9.608	6.672	5.149	4.614	3.623	3.429
OA	3.680	4.426	5.845	9.346	20.049	18.274	11.024	7.528	5.453	4.598	3.993	3.536	3.389
OR	2.724	3.393	4.652	7.328	15.510	15.062	10.206	5.879	4.389	3.881	3.522	3.100	4.000
$\mathit{c}=\mathbf{1},\mathit{r}=\mathbf{2}$					$\mathit{\alpha }=\mathbf{2},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.12	0.18	0.24	0.28	0.38	0.42	0.48	0.54	0.6	0.66	0.72	0.78	0.84
Sol	4.733	6.418	10.601	18.015	21.900	12.759	8.160	5.753	4.537	4.059	3.868	3.471	3.429
OA	3.911	5.140	8.152	14.868	16.413	10.208	6.396	4.823	4.194	3.628	3.460	3.229	3.000
OR	2.912	3.972	6.327	10.711	13.418	8.477	4.984	3.833	3.157	2.794	2.546	2.500	Null
$\mathit{c}>\mathit{r}:$
$\mathit{c}=\mathbf{3},\mathit{r}=\mathbf{2}$					$\mathit{\alpha }=\mathbf{7},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.65	0.66	0.72	0.78	0.84	0.9
Sol	3.911	4.511	5.332	6.422	8.088	10.913	16.426	32.571	36.403	29.336	13.765	8.543	7.140
OA	3.457	3.799	4.323	5.068	6.141	8.104	12.119	24.871	25.874	20.474	10.281	7.240	4.645
OR	2.570	2.910	3.344	3.907	4.867	6.274	9.379	18.112	19.234	17.288	8.740	4.880	4.000
$\mathit{c}=\mathbf{2},\mathit{r}=\mathbf{1}$					$\mathit{\alpha }=\mathbf{9},\mathit{\beta }=\mathbf{2}$
$\mathit{\vartheta }$	0.18	0.24	0.3	0.36	0.42	0.48	0.54	0.6	0.62	0.72	0.78	0.84	0.9
Sol	3.815	4.305	4.963	5.782	6.950	8.716	11.345	16.756	31.361	43.763	37.012	15.414	9.261
OA	3.446	3.740	4.151	4.683	5.392	6.558	8.474	12.322	23.541	33.944	25.088	10.330	7.312
OR	2.442	2.682	2.984	3.358	4.006	4.910	6.421	9.459	17.515	24.158	20.682	9.183	4.500

Bala, V., & Goyal, S. (1998). Learning from neighbours. The Review of Economic Studies, 65(3), 595–621. https://doi.org/10.1111/1467-937X.00059

 Web of Science ®Google Scholar

Molavi, P., Tahbaz-Salehi, A., & Jadbabaie, A. (2018). A theory of non-Bayesian social learning. Econometrica, 86(2), 445–490. https://doi.org/10.3982/ECTA14613

 Web of Science ®Google Scholar

Harel, M., Mossel, E., Strack, P., & Tamuz, O. (2021). Rational groupthink. The Quarterly Journal of Economics, 136(1), 621–668. https://doi.org/10.1093/qje/qjaa026

 Web of Science ®Google Scholar

Huang, W., Strack, P., & Tamuz, O. (2021). Learning in repeated interactions on networks”. arXiv:2112.14265v2.

 Google Scholar