The Curious Case of the Cross-Sectional Correlation

Figures & data

Figure 1. Example of Cattel’s databox, showing how data can be thought to come from three different dimensions: variables (here only two), persons, and occasions. It further shows that a cross-section of two variables consists of many individuals at one occasion, whereas a person-specific (N = 1) study consists of many occasions from a single person.

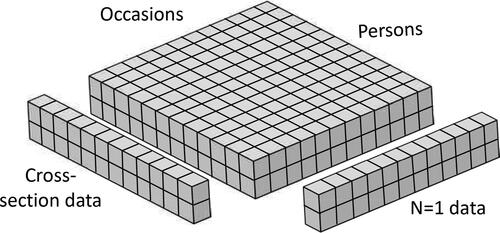
Table 1. Five correlations that can be used to describe the way X and Y are related.

Equation	Description
$\rho =\frac{{\sigma }_{X,Y}}{{\sigma }_X{\sigma }_Y}=\frac{{\sigma }_{BX}}{{\sigma }_X}\frac{{\sigma }_{BY}}{{\sigma }_Y}{\rho }_B+\frac{{\sigma }_{WX}}{{\sigma }_X}\frac{{\sigma }_{WY}}{{\sigma }_Y}{\rho }_W$	Cross-sectional correlation based on correlating the scores on X and Y (at a particular occasion t) across persons
${\rho }_B=\frac{{\sigma }_{BX,BY}}{{\sigma }_{BX}{\sigma }_{BY}}=\frac{\mathit{cov}(\mathrm{E}[X|P],\mathrm{E}[Y|P])}{\sqrt{\mathit{var}(\mathrm{E}[X|P])}\sqrt{\mathit{var}(\mathrm{E}[Y|P])}}$	Between-person correlation based on correlating the person-specific means on X and Y across persons
${\rho }_W=\frac{{\sigma }_{WX,WY}}{{\sigma }_{WX}{\sigma }_{WY}}=\frac{\mathrm{E}[\mathit{cov}(X,Y|P)]}{\sqrt{\mathrm{E}[\mathit{var}(X|P)]}\sqrt{\mathrm{E}[\mathit{var}(Y|P)]}}$	Within-person correlation based on correlating the occasion-specific deviations from person-specific means on X and Y (at a particular t) across persons
${\kappa }_p=\frac{\mathit{cov}(X,Y|P)}{\sqrt{\mathit{var}(X|P)}\sqrt{\mathit{var}(Y|P)}}$	Person-specific correlation based on correlating X and Y over time for person P = p (i.e., Cattell’s intra-individual correlation)
$\kappa =\mathrm{E}[\frac{\mathit{cov}(X,Y|P)}{\sqrt{\mathit{var}(X|P)}\sqrt{\mathit{var}(Y|P)}}]$	Average person-specific correlation based on taking the average of the person-specific correlation κp across persons

Note: Mathematical expressions and substantive descriptions of five different correlations that can be used to summarize the relation between variables X and Y. The first three correlations (cross-sectional, between-person and within-person) are associated with the known expression provided in Eq. (7). The person-specific and average person-specific correlations come from the literature inspired by Cattell’s work.

Figure 2. Illustration of how the average person-specific correlation κ (dashed line) falls in between the person-specific correlations that characterize the two subpopulations (i.e., κ_p, represented by the two solid lines), and how the within-person correlation ρ_W from the expression for the cross-sectional correlation (dotted line) deviates from this, depending on the person-specific variances. $Q=1/\sqrt{\mathit{var}(X|P)\mathit{var}(Y|P)}$ in the second subpopulation is varied by varying the person-specific variances of X and Y, while all else (i.e., person-specific covariance in second subpopulation, and person-specific variances and covariance in first subpopulation) are held constant.

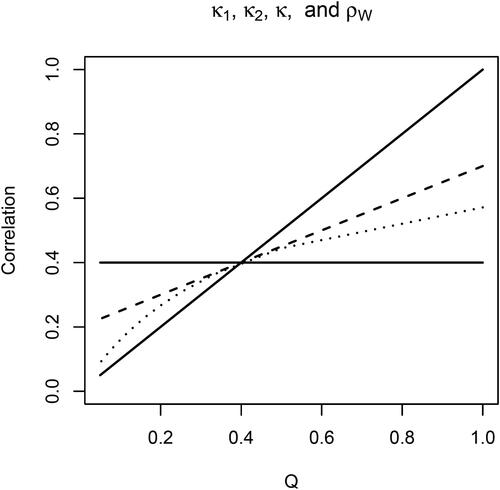
Figure 3. Heatmap showing the sum of the two weights (i.e., ${\eta }_{BX}{\eta }_{BY}+{\eta }_{WX}{\eta }_{WY}$ as a function of the intraclass correlation (i.e., proportion of BP variance) in X (i.e., ${\eta }_{BX}^2$) and Y (i.e., ${\eta }_{BY}^2$). Lighter colors indicate higher values.

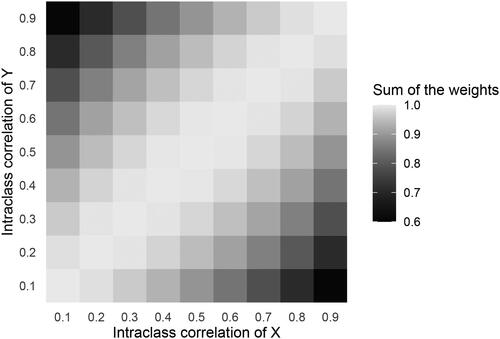
Figure 4. Solid (purple) lines represent the cross-sectional correlation plotted against intraclass correlation of X (i.e., ${\eta }_{BX}^2$). Darkest line is for an intraclass correlation of Y (i.e., ${\eta }_{BY}^2$) of 0.1, while the lightest line represents the scenario when it is 0.9. Dashed (red) line represents the WP correlation ρ_W; dotted (blue) line represents the BP correlation ρ_B.

Table 2. Seven examples illustrating the relation between various correlations.

Parameter	Type	Example 1	Example 2	Example 3	Example 4	Example 5	Example 6	Example 7
${\eta }_{BX}^2$	set	0.4	0.1	0.2	0.2	0	0.4	0.4
${\eta }_{BY}^2$	set	0.5	0.9	0.8	0.8	0	0.5	0.4
$\mathit{cov}(X,Y|P)$	set	1/1	1/1	4/5	1/5	1/1	1/1	1/1
$\mathit{var}(X|P)=\mathit{var}(Y|P)$	set	1.25/5	1.25/5	10/10	2/10	1.25/5	1.25/5	1.25/5
κp	comp.	0.8/0.2	0.8/0.2	0.4/0.5	0.5/0.5	0.8/0.2	0.8/0.2	0.8/0.2
κ	comp.	0.500	0.500	0.450	0.500	0.500	0.500	0.500
ρW	comp.	0.320	0.320	0.450	0.500	0.320	0.320	0.320
ρB	set	0.500	0.500	0.450	0.500	–	0	0.320
ρ	comp.	0.399	0.246	0.360	0.400	0.320	0.175	0.320
$\widehat{\rho }$	est.	0.393	0.229	0.354	0.408	0.340	0.168	0.317

Note: Seven examples that illustrate how and why the cross-sectional correlation ρ can differ from the average person-specific correlation κ. Quantities of interest are: the intraclass correlations ${\eta }_{BX}^2$ and ${\eta }_{BY}^2;$ the person-specific covariances $\mathit{cov}(X,Y|P),$ variances $\mathit{var}(X|P)$ and $\mathit{var}(Y|P),$ and correlations κ_p (the values of these are specified for two subpopulations, before and after the/; these subpopulations each make up exactly half of the total population); the average person-specific correlation κ; the within-person correlation ρ_W; the between-person correlation ρ_B; the cross-sectional correlation ρ, and the estimated cross-sectional correlation $\widehat{\rho }$ based on simulated data of 1,000 persons. Second column indicates whether a particular parameter was set to a certain value, computed (comp.) based on other parameters, or estimated (est.) from the simulated data.