An experimental study of methods for the analysis of variance components in the inference of laboratory information

Figures & data

Figure 1. The components and design of the study.

Figure 2. Within and between series variations based on series of five measurements on five occasions (days). One of the results (as shown in the figure) in the first series was regarded as an outlier and not used for further calculations.

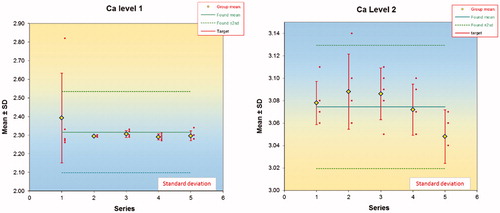
Figure 3. Left panel. The standard deviation (target value 1.12) and confidence interval calculated by the simulation model 5. Each number of observations was simulated 100 times. The vertical line represents the suggested minimal number of observations needed. The corresponding graphs from the other simulations followed the same pattern. Right panel. Standard deviations for ALT, ALP and Ca were calculated using the 100 duplicates using the Dahlberg formula. Solid lines are standard deviations, dotted lines confidence intervals.

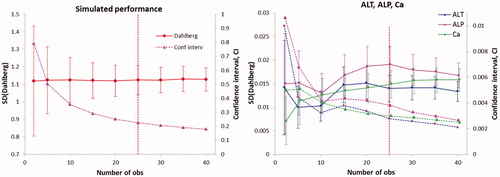
Table 1. Details of analysis of variance components.

	ALT Level 1	ALT, level 2	ALP Level 1	ALP Level 2	Ca Level 1	Ca Level 2
Between series df	4	4	4	4	4	4
Within series df	20	20	20	20	19	20
Number of observations	25	25	25	25	24	25
Average	0.73	2.32	1.38	4.93	2.29	3.07
SEM	0.002	0.004	0.003	0.011	0.004	0.005
Repeatability (s)	0.009	0.021	0.016	0.054	0.021	0.025
Pure between series (s)	0.005	0.001	0.005	0.010	–	0.012
Total imprecision (s)	0.011	0.021	0.017	0.055	0.021	0.028
Repeatability (%CV)	1.3	0.92	1.2	1.1	0.90	0.81
Pure between series (%CV)	0.63	0.05	0.36	0.20	–	0.38
Total imprecision (%CV)	1.45	0.93	1.22	1.11	0.90	0.89

The outlier shown in Figure 2 was excluded from the summary calculations. The ‘pure between series imprecision’ was obtained by correcting the between group ‘mean square’ of the ANOVA analysis [4] for the contribution of the repeatability variance. The between group mean square (MS_b) was smaller than that of the within group for the Ca-measurements of the low concentration material and therefore not presented.

Table 2. The imprecision (standard deviation) calculated across all observations and using the method of analysis of variance components from 2 to 6 daily IQC measurements of control material, comprising 83 observations.

	ALT µkat/L		ALP µkat/L		Calcium mmol/L
Average	0.74	2.32	1.38	4.95	2.29	3.08
Across (s)	0.013	0.021	0.020	0.054	0.018	0.021
%CV	1.76	0.90	1.42	1.09	0.77	0.66
Repeatability (s)	0.009	0.022	0.017	0.054	0.018	0.021
Pure Reproducibility (s)	0.009	–	0.009	–	–	–
Intra-laboratory (s)	0.013	0.022	0.020	0.054	0.018	0.021

Table 3. Properties of duplicate measurements of patient samples.

	ALAT	ALP	Ca
Count	100	100	100
Average	1.84	3.46	2.32
Median	0.69	2.05	2.36
IQR	25.00	75.00	75.00
10 percentile	0.37	1.41	2.21
90 percentile	1.71	4.70	2.47
Maximum observations	10.3	16.6	3.2
Minimum observations	0.1	0.5	1.3
s(X) (Dahlb)	0.016	0.023	0.016
%CVD(X)	3.26	0.69	0.72
Maximum difference	0.10	0.11	0.06
Average difference	0.0004	−0.0002	−0.0008
Student tdep	0.17	0.06	0.35
p (2-tail)	.863	.951	.729
s(X) (ExpD)	0.016	0.023	0.016

The repeatability (bold) was calculated by Dahlberg’s formula and the expanded formula (ExpD). s(X) and %CV(X) represent the absolute and relative Dahlberg uncertainty, respectively.

Table 4. Summary of the simulations of a normally distributed set of 0.5 × 10⁶ simulated results (Orig) from an average of 10 and a standard deviation of 1 and a simulated repeated series with an assumed average difference of 0.25 times a random normality probability function (Rep).

	Basic	Rand add		Non-rand	Bias add	Basic	Rand add		Non-rand	Bias add
	10	1	0.25	0		10	1	0.25	2
Set values	Orig	Rep	Diff	Rep + bias	Diff	Orig	Rep	Diff	Rep + bias	Diff
$\overline{x}$	9.9993	9.9992	−0.0001	9.9992	−0.0001	9.9987	9.9983	−0.0004	11.9983	1.9996
Sumsq(x1–x2)	5491200	50521745	31249	50521745	31249	50485271	50512924	31265	72508976	2030396
Stand dev (s)	0.9993	1.0306	0.2500	1.0306	0.2500	0.9996	1.0309	0.2501	1.0309	0.02501
Var Dahlberg			0.0313		0.0313			0.0313		2.0304
Var Expanded					0.0313					0.0313

A non-random difference, equal to zero and 2 (20%), right panel illustrates how a traditionally calculated SD_Dahl differs from that using the expanded Dahlberg formula, which gives an SD_ExpD devoid of an influence of the average of the bias. Finally, calculated quantities are in bold. The negligible effect of a random error between the original and repeated measurement is clearly shown as the variance of the repeats as the sum of the variances of the difference and original series (see text).

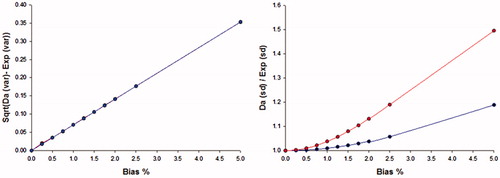
Figure 4. The difference between the Dahlberg standard deviation and that of the Dahlberg expanded formula (as the square root of the difference between the variances), left panel. The difference is linearly related to the relative bias and independent of the assumed random variation of the samples. The ratio (right panel) between the standard deviation estimated by the Dahlberg and Expanded Dahlberg formulas. The random difference between series was 2.5%.

Kallner A, Theodorsson E. Repeatability imprecision from analysis of duplicates of patient samples. Scand J Clin Lab Invest 2020;80(1):73-80.

 Google Scholar