Simulation of different applicator positions for treatment of a presacral tumour

Figures & data

Figure 1. Model of the phantom used for this calculation study in sagittal and transverse direction. The central point (0, 0, 0) is marked as little orange spot and the axes in the sagittal picture show the distances in cm. The x-axis goes right–left, with positive values on left (L). The y-axis is anterior–posterior with positive values posterior (P) and the z-axis goes caudal-cranial with positive values cranial or head (H), building a L-P-H system. The presacral tumor is shown in red, located posterior from the centre of the model with its centre of gravity about 2 cm posterior to the centre of the model. Calculated fatty tissue is a small equidistant border around the elliptic phantom material. Phantom material is calculated as muscle tissue.

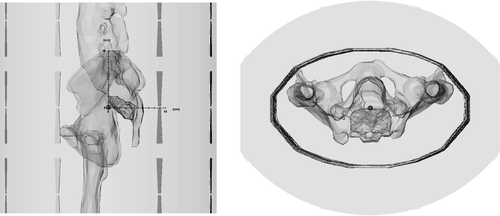
Table I.  Physical and physiological properties used for the calculations in Amira-HyperPlan [see also [14].

Tissue	Dielectric constant	Electrical conductivity (S/m)	Perfusion (ml/100g/min)	Density (g/cm^3)	Heat capacity (J kg K^−1)	Thermal conductivity (W/m K)	Max temp (°C)
Fat	10	0.04	20	900	3500	0.21	44
Muscle	80	0.8	30	1000	3500	0.642	44
Bone	9	0.02	10	1600	1000	0.436	44
Target	80	0.8	8	1000	3500	0.642	50
Bolus	78	0.001	0	1000	3500	0.642	44

First line shows the property with its unit and the first row shows the tissue used in the model. Fatty tissue is just the small equidistant layer around the phantom material, which in this study is calculated as muscle tissue.

Table II.  Definition of the calculated thermal parameters T₉₀, T₅₀, hot spot volume, total power, sensitivity.

Parameter	Definition
T90	Temperature reached by at least 90% of the tumour volume
T50	Temperature reached by at least 50% of the tumour volume
Hot spot volume	Volume of normal tissue with temperature above 42°C
Total power	Power in the patient model, restricted by 44°C in normal tissue
Sensitivity of phase/amplitude adjustment	Mean deviation of the calculated T90 in°C by changing amplitudes ±10% and phases up to ±10° around this adjustment for 1000 randomized samples (corresponding to the typical variation of feedpoint characteristics)
δ T90	Difference of T90 reached by standard steering and optimised steering at the same position
δ Total power	Difference of Total power reached by standard steering and optimised steering at the same position
Power per T90	Additional amount of power needed to increase T90 for 1°C at a particular position, calculated from δ Total power/δ T90

Out of these parameters the values δ T₉₀, δ Total power and power per T₉₀ were calculated separate for each position as difference between the value (T₉₀ or Total power) reached with optimised steering minus the value reached with standard steering. The last parameter is the quotient of the difference of Total power and the difference of T₉₀.

Table III.  Mean, median and standard deviation in cm of the applicator-shifting in x-(lateral), y-(posterior) and z-(longitudinal) direction during the 112 treatment sessions of the first 10 male and 10 female patients (without positioning device) together with the numbers of treatments per patient.

	Range x (cm)	Range y (cm)	Range z (cm)	No of treatments
Mean–all	1.1	2.0	6.4	5.6
Mean–male	1.0	1.9	7.9	6.3
Mean–female	1.1	2.2	4.2	4.5
Median–all	1.0	1.9	5.5	5
Median–male	0.9	1.9	6.9	5
Median–female	1.2	2.0	4.3	4.5
SD–all	0.5	1	3.6	2.2
SD–male	0.5	0.9	3.9	2.5
SD–female	0.4	1.2	1.1	0.9

All patients were treated with a pelvic regional hyperthermia in the Sigma-Eye/MRI applicator. These ranges were retrospectively determined from the magnitude pictures of the MR thermometry measurements. The largest variation in positioning is found for z (±6 cm), followed by y (±2 cm) and x (±1 cm). The biggest difference between male and female patients is in z direction, which can be declared by the more conical form of a male pelvic region in comparison to the more elliptic form of a female pelvis (see text). Due to the conical form of a male pelvis a position deviation in z-direction is more likely.

Table IV.  Mean values and standard deviation of T₉₀, T₅₀, sensitivity and hot spot volume for all different adjustments used in this study. It is clearly shown, that the plans with amplitude and phase optimisation (A plan) result in the highest temperatures, but also in the highest sensitivity to small changes of the amplifier control parameters phase and amplitude. Permitted total power is highest for the optimisation strategy with the largest number of degrees of freedom (A plans), whereas the hot spot volume decreases by optimisation. The lowest total power and the highest hot spot volumes are reached with standard steering, which have the lowest index temperatures and also the lowest sensitivity.

Opt. method		T90 (°C)	T50 (°C)	Sensitivity (°C)	Total power (W)
Mean ± SD	n	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD	Hot Spot volume (ml)
Plan A	430	40.2 ± 0.36	40.9 ± 0.41	0.6 ± 0.11	1530 ± 6	164 ± 7
Plan B	430	39.5 ± 0.49	40.0 ± 0.58	0.3 ± 0.09	1280 ± 9	176 ± 8
Standard setup	430	38.4 ± 0.55	38.7 ± 0.65	0.04 ± 0.04	964 ± 10	260 ± 9

Figure 2. Dependency of 430 calculated T₉₀ values on the x- (lateral) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points show the value for y = 0 and z = 0, with bars the range of minimal and maximal T₉₀ values (for y ≠ 0 and z ≠ 0) is shown. The central x-values (x = 0) result in the best T₉₀ values after optimisation. The standard adjustments show a higher difference between the best central and the lateral positions than the optimised adjustments. The highest values are reached by A plans, which have the largest number of degrees of freedom.

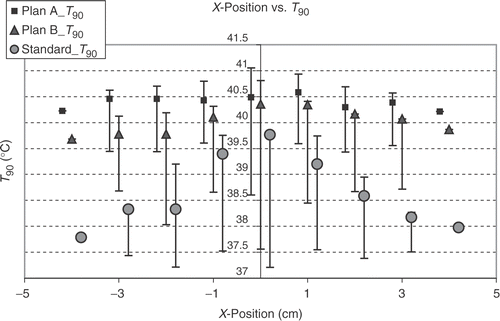
Figure 3. Dependency of 430 calculated T₉₀ values on the y-(anterior-posterior) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points show the values for x = 0 and z = 0, with bars the range for x ≠ 0 and z ≠ 0 is shown. The optimised adjustments show a clear dependency on the y-position with the optimum around the centre. The standard adjustments show a similar dependency on the y-position. For the same number of different positions at a particular y-position the range of T₉₀ is smallest for A plans and greatest for standard steering. At the centre of gravity of the tumour at position y = 2 and also the next more posterior located position (y = 3), A plans show the best T₉₀. The lowest T₉₀ for each adjustment are at position y = −5.

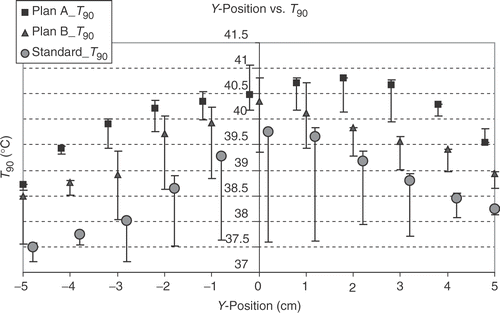
Figure 4. Dependency of 430 calculated T₉₀ values on the z-(longitudinal) positions by optimising according A plans (with amplitude and phase optimisation, squares), B plans (only phase optimisation, triangles) and the standard setup (circles). Points stand for x = 0 and y = 0, with bars the range for x ≠ 0 and y ≠ 0 is shown. (For z = 6 and z < −5 there is only one position calculated.) The optimised adjustments indicate two suitable positions to increase T₉₀: at z = 0 (especially B plans and standard adjustments) and even better for z = 8 cm (in cranial direction). For the standard adjustments the range around z = 0 shows nearly a plateau from −3 to 2 cm. At z > 6 there is no improvement of the T₉₀ values for standard adjustment. For A plans and z = 0 only positions with y ≠ 0 yield better T₉₀ than the adjacent z positions, but for z = 8 there is a clear improvement of T₉₀.

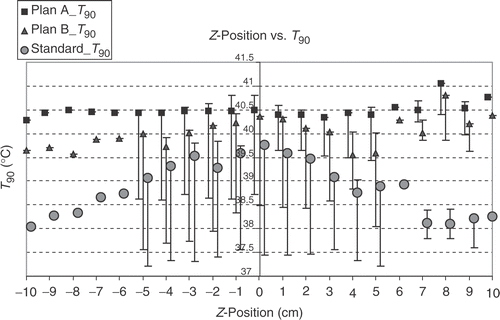
Table V.  Correlation among the thermal parameters T₉₀ and T₅₀, total power, sensitivity (to adjustment changes), hot spot volume, differences δ of T₉₀ and total power (optimised minus standard adjustment) and power needed to raise T₉₀ by 1°C (power per °C T₉₀). The correlation and significance was calculated with Spearman-Rho with the software SPSS 12.0. There exists a close linear correlation between the index temperatures T₉₀ and T₅₀. Total power has a good linear correlation with T₉₀ only for B plans and standard steering but not for A plans. Hot spot volume correlates with total power just for standard steering. A linear correlation exists for δ total power vs power per °C T₉₀, for A plans more than for B plans. There is only a weak linear correlation between δ T₉₀ vs. δ total power and a negative correlation between T₉₀ and the power per °C T₉₀. There is no close linear correlation between sensitivity and T₉₀, total power or hot spot volume.

Parameters	A plan r; p	B plan r; p	Standard plan r; p
T90 vs. T50	0.98; 0.001	0.995; 0.001	0.99; 0.001
T90 vs. total power	0.46; 0.001	0.84; 0.001	0.71; 0.001
T90 vs. Hot Spot volume	0.58; 0.001	0.47; 0.001	0.62; 0.001
T90 vs. sensitivity	0.38; 0.001	0.56; 0.001	0.43; 0.001
Total power vs. sensitivity	0.30; 0.001	0.48; 0.001	0.41; 0.001
Total power vs. Hot Spot vol.	0.25; 0.001	0.44; 0.001	0.69; 0.001
Hot Spot vol. vs. sensitivity	0.35; 0.001	0.014; n.s.	0.41; 0.001
δ T90 vs. δ total power	0.46; 0.001	0.54; 0.001	–
δ Total power vs. pow. per °C T90	0.84; 0.001	0.65; 0.001	–
T90 vs. power per °C T90	−0.24; 0.001	−0.18; 0.001	–

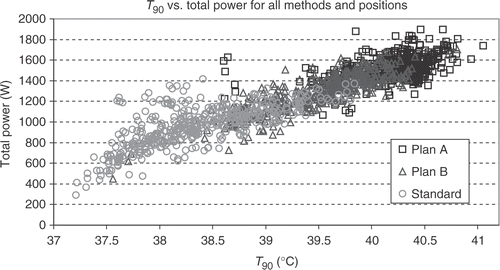
Figure 5. Scatterogram of T₉₀ vs. total power. For high T₉₀'s a high total power is necessary, no matter which kind of phase control is used (there are only very few exceptions, where the power is high but T₉₀ is relatively low). Optimised phase and amplitude control reduces hot spots, so that the total power can be elevated and T₉₀ increases. The lowest T₉₀ for all adjustments is at position x = 0, y = −5 and z = −5 with the centre of the applicator just behind the mid-pubic symphysis. The power at this position is low for standard steering and B plans but quite high for A plans, adding only about 1.4°C to T₉₀ with about 1300 W additional power in comparison to standard steering and 1.05°C with about 1200 W additional power in comparison to B plan steering. One problem is permanent: only 150 W per antenna is available from the amplifier, so these calculated power levels for A plans can not be used. Amplitude optimisation is done by amplitude reduction of several antennas, and maximum power with all 12 antennas (with full power) is restricted to 1800 W.

Sreenivasa G, Gellermann J, Rau B, Nadobny J, Schlag P, Deuflhard P, Felix R, Wust P. Clinical use of the Hyperthermia treatment planning system Hyperplan to predict effectiveness and toxicity. Int J Radiat Oncol Biol Phys 2003; 55: 407–419

 PubMed Web of Science ®Google Scholar