Regional deep hyperthermia: quantitative evaluation of predicted and direct measured temperature distributions in patients with high-risk extremity soft-tissue sarcoma

Figures & data

Table 1. Patient characteristic, including the number of the CT slices used for manual and semi-automatic segmentation of structures.

Patient	Gender	Diagnosis	# of CT slices	# of catheters	Tumor volume/cm³
1	m	leiomyosarcoma	178	3	511
2	f	rhabodomysarcoma	120	2	290
3	f	pleomorphic sarcoma	100	2	226
4	m	Synovial sarcoma	191	1	501
5	m	pleomorphic sarcoma	131	2	188

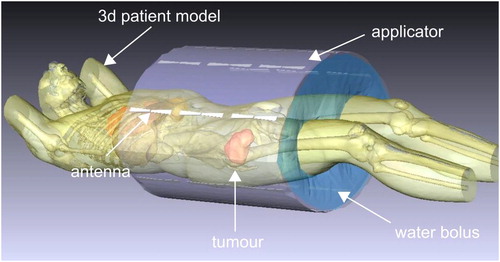
Figure 1. 3D volume rendering of three exemplary STS patients with implemented catheters in the tumor.

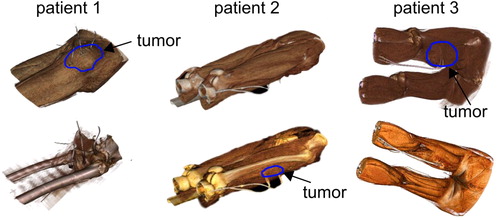
Table 2. Applicator setting for both patient treatments and thermal simulations.

Patient	Focus (x,y)/cm			power/watt
	Treatment	HTP_I	HTP_II	Treatment	HTP_I	HTP_II
1	(6,2)	(0,0)	(0,0)	730	613	730
2	(4,0)	(0,−3)	(0,−3)	521	451	521
3	(−3,−1)	(−4,−2)	(−4,−2)	336	334	336
4	(−5,1)	(−8,2)	(−8,2)	440	696	440
5	(−5,5)	(−5,1)	(−5,1)	420	604	420

Figure 2. Thermal simulation setup in the software SigmaHyperPlanTM.

Figure 3. Flowchart illustrating the evaluation procedure of both treatment and simulated temperature data.

Figure 4. Measured temperatures along the tumor catheters for all treated patients. Note that the height of each boxplot represents the measured values over the entire treatment time for each catheter position. The red points are the calculated mean values and the black bold line in the boxplot gives the median value. The position 0 cm means that the sensor was located at the catheter tip. The temperature mapping was in 1 cm steps.

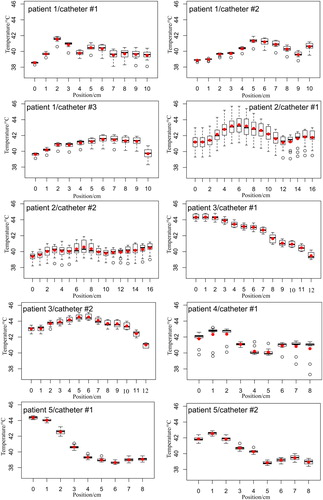
Figure 5. Calculated temperatures using the data from Figure 1. Note that the width of the boxplot reflects the time-averaged temperature values for all mapping positions. The red point is the computed mean value.

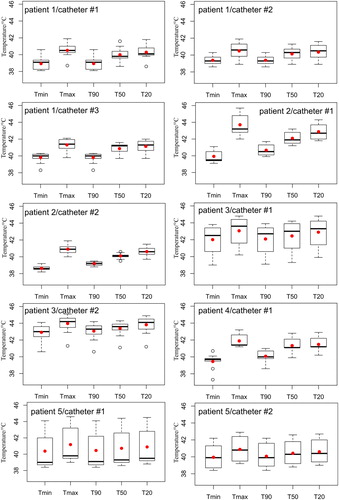
Table 3. Thermal dose (CEM43T90) values for both patient treatments and thermal simulations.

	Patient 1			Patient 2		Patient 3		Patient 4		Patient 5
	Catheter
	1	2	3	1	2	1	2	1	1		2
HTP_I	3.8	3.8	0.9	0.2	0.2	0.2	0.9	0.9	15		0.9
HTP_II	3.8	0.9	0.2	0.2	0.2	60	3.8	0.2	3.8		3.8
Treatment	0.2	0.3	0.6	2.9	0.3	30	55	1.4	0.1		0.2

Table 4. Temperature change ($\Delta \mathrm{T}$) of T90 above the patient body temperature of 37 °C.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	Catheter
	1	2	3		1	2	1	2	1	1		2
HTP_I	4	4	3		2	2	2	3	3	5		3
HTP_II	4	3	2		2	2	6	4	2	4		4
Treatment	2	2	3		3	2	5	6	3	3		3

Figure 6. Coronal cross-sections thermal maps, overlaid on CT images, of the five STS patients generated from the HTP_I. The maps show relative inhomogeneous temperature distributions within the HT-GTV. Note that some hot spots are developed either within the muscle tissue or close to the bone.

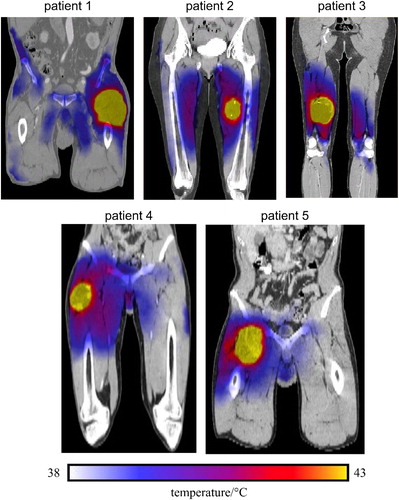
Table 5. Temperatures obtained from the HTP_I. Note that the core body temperature is 37 °C.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	Catheter
	1	2	3		1	2	1	2	1	1		2
Tmin	38	39	37		37	37	40	38	38	38		37
Tmax	45	48	48		48	48	46	43	49	48		48
T90	41	41	40		39	39	39	40	40	42		40
T50	44	46	45		44	44	43	41	46	47		48
T20	44	48	47		47	47	45	42	48	48		48
Tmean	43	45	45		43	43	43	42	45	46		46

Table 6. Temperatures calculated from the thermal simulation HTP_II.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	Catheter
	1	2	3		1	2	1	2	1	1		2
Tmin	37	38	37		37	37	38	39	40	37		37
Tmax	46	47	46		48	47	49	49	47	48		48
T90	41	40	39		39	39	43	41	39	41		41
T50	44	44	43		46	43	47	46	44	46		46
T20	45	47	44		47	45	48	48	45	48		47
Tmean	44	44	42		45	42	46	46	43	45		45

Table 7. Temperature differences between patient treatment and thermal simulation HTP_I.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	$\Delta \mathrm{ }(°\mathrm{C})$
	Catheter
	1	2	3		1	2	1	2	1	1		2
Tmin	1	0	3		3	1	2	5	1	2		3
Tmax	4	8	7		5	8	3	1	7	7		7
T90	2	2	0		1	1	3	3	0	2		0
T50	4	6	4		2	5	1	2	5	6		8
T20	4	8	6		5	7	3	2	7	7		7
Tmean	3	5	4		2	4	1	1	4	5		6

Table 8. Temperature differences between patient treatment and thermal simulation HTP_II.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	$\Delta \mathrm{ }(°\mathrm{C})$
	Catheter
	1	2	3		1	2	1	2	1	1		2
Tmin	2	2	2		3	1	4	6	2	3		3
Tmax	5	7	5		5	7	6	5	5	7		7
T90	2	1	1		1	1	1	2	1	1		1
T50	4	4	2		4	4	5	3	3	5		6
T20	5	7	3		5	5	6	5	4	7		6
Tmean	4	4	1		4	3	4	3	2	4		5

Table 9. Differences of $\Delta \mathrm{T}$ for both thermal simulations, where the patient treatment served as a reference.

	Patient 1			Patient 2			Patient 3		Patient 4		Patient 5
	$\Delta (°\mathrm{C})$
	Catheter
	1	2	3		1	2	1	2	1	1		2
HPT_I	4	4	3		2	2	2	3	3	5		3
HTP_II	4	3	2		2	2	6	4	2	4		4

Figure 7. 2D Photograph images of the lamp phantom positioned inside the SIGMA-Eye applicator, where the applicator settings of patient treatment, HTP_I and HTP_II were applied. The hot spot in the phantom presents the 2D electrical field distributions using 400 watts for all phantom measurements. Note that the field distributions of HPT_I and HTP_II feature a significant deviation with respect to the shape of the distribution and the hot spot position, when they compared to the treatment settings.

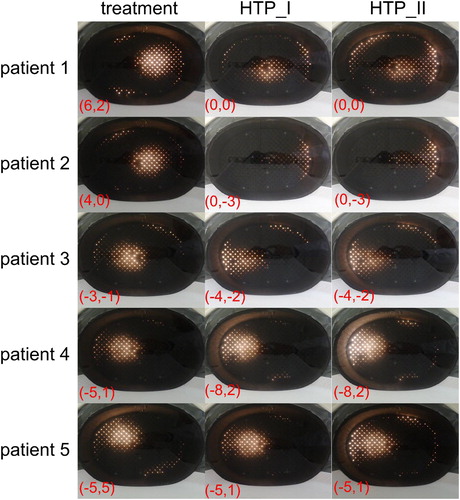
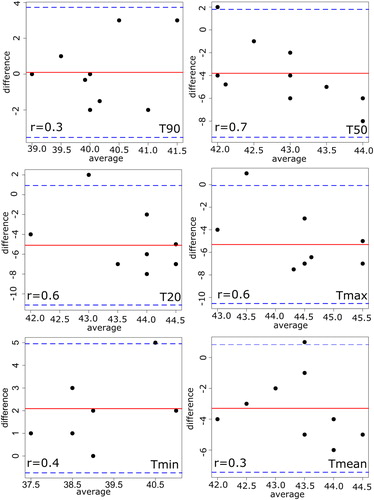
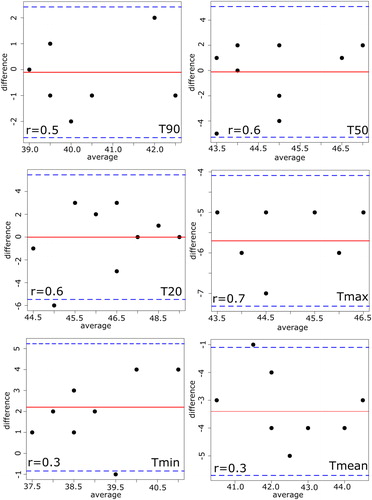
Figure 8. Bland–Altman plot with the corresponding correlation coefficient (r) between the real patient treatment and thermal simulation HTP_I. The solid line shows the mean $m$ of differences between both methods and the thin dashed lines show $m\pm 2\sigma$ of confidence interval of 95%, where $\sigma$ the standard deviation of the differences. Note that values with the same differences will be plotted on the top of each other.

Figure 9. Bland–Altman plot with the corresponding correlation coefficient (r) between the real patient treatment and thermal simulation HTP_II.