Open access
184
Views
0
CrossRef citations to date
0
Altmetric
Research Article
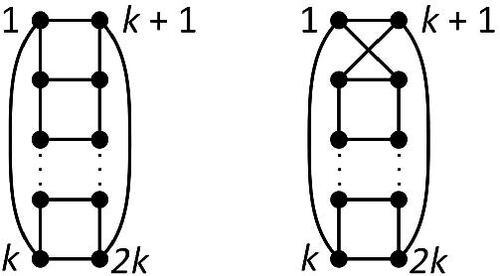
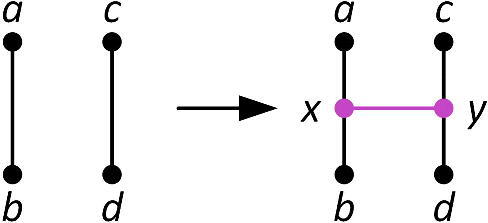
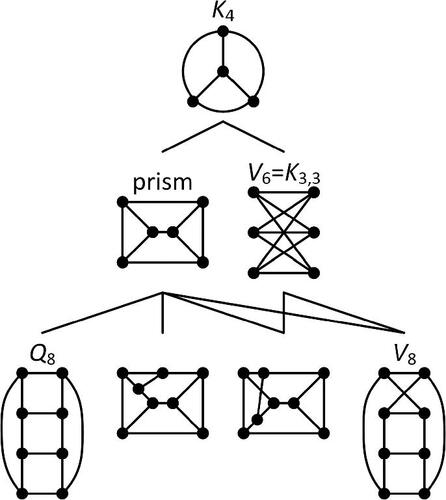
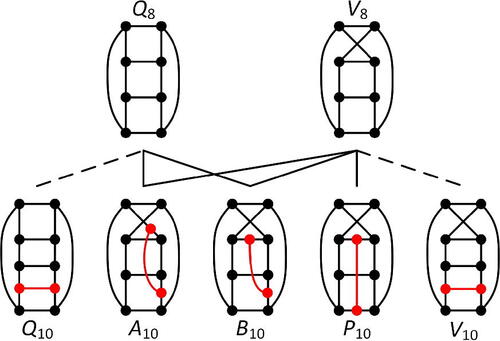
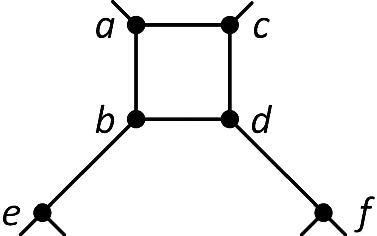
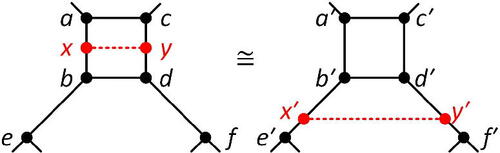
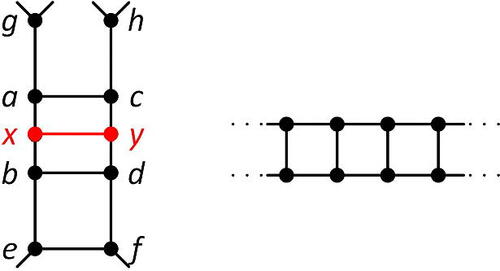
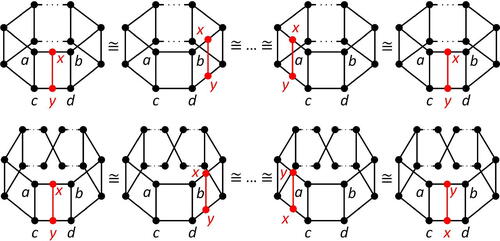
On cyclically 4-connected cubic graphs
R. J. Kingana Bloomberg LP., New York, NY, USA
& S. R. Kinganb Department of Mathematics, Brooklyn College, Brooklyn, NY, USA;c CUNY Graduate Center, New York, NY, USACorrespondence[email protected]
Received 17 Feb 2024, Accepted 11 Mar 2024, Published online: 08 Apr 2024
Related research
People also read lists articles that other readers of this article have read.
Recommended articles lists articles that we recommend and is powered by our AI driven recommendation engine.
Cited by lists all citing articles based on Crossref citations.
Articles with the Crossref icon will open in a new tab.