A diluted version of the problem of the existence of the Hofstadter sequence

Figures & data

Figure 1. The first eight rows of the triangular array of sets $\mathcal{T}$. Here, i and n index the sets horizontally and vertically respectively, with $i=0,\dots ,n-1$. The set of consecutive integers $k,\dots ,l$ is written $\{k:l\}$ and as $\{k\}$ when l = k.

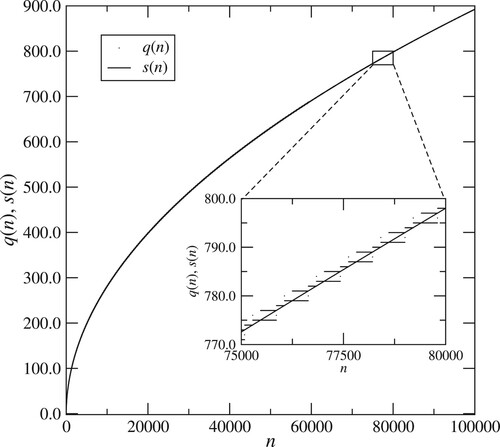
Figure 2. Plot of $q(n)$, black dots, for $f(n)=\lfloor 5-5/\sqrt{n}\rfloor$, so that $f(n)\to 4$ as $n\to \mathrm{\infty }$. According to the argument in Section 5.2, we expect that $q(n)\sim \sqrt{8n}-2:=s(n)$, this curve being plotted as a continuous black line. The approximation appears to hold remarkably well, the two plots being almost exactly superimposed. Inset: enlargement of the region $75000\le n\le 80000$.

Figure 3. Plot of $q(n)-n/\sqrt{2}$ for $n=1,\dots ,160000$, with $f(n)=\lfloor \frac{n}{2}\rfloor$. Two pairs of self-similar regions $a_1,a_2$ and $b_1,b_2$ are shown – see text.

Figure 4. Plot of the difference of $q(n)=Q(\lfloor n/2\rfloor )$ and $q_1(n)=Q(\lfloor n/2\rfloor +\delta (n-16))$. The idea is that $q_1(n)$ is a slightly perturbed version of $q(n)$. The effect of the perturbation persists, at least until $n=2^{19}$.