Figures & data
Table 1. Summary of studied cases.
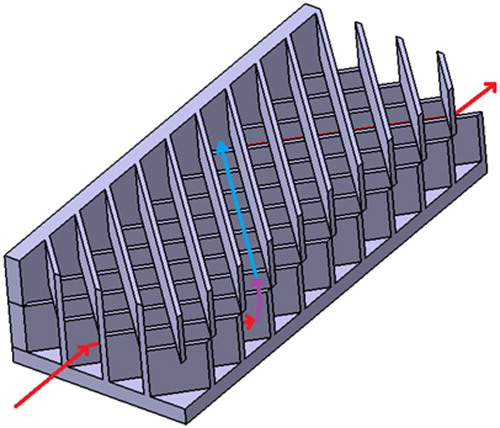
Figure 4. Details of rotational case about (a) the rotation axis and direction of rotation and (b) leading and trailing surfaces.
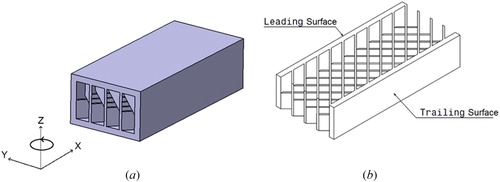
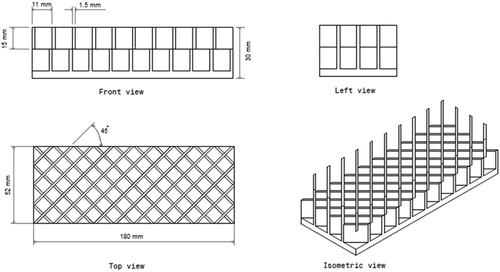
Table 2. Dimension of test geometry.
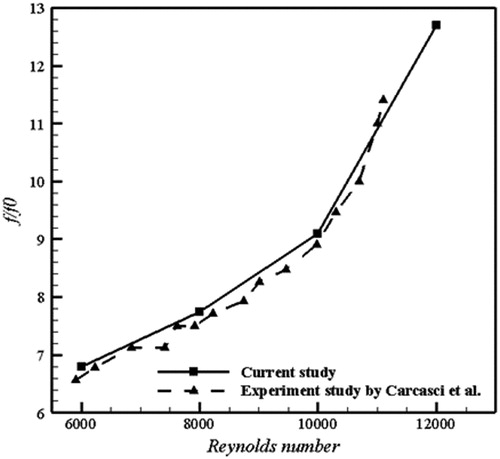
Figure 6. Nusselt number ratio comparison with Carcasci [Citation10] and Saha [Citation13] for different Reynolds number.
![Figure 6. Nusselt number ratio comparison with Carcasci [Citation10] and Saha [Citation13] for different Reynolds number.](/cms/asset/e2f94738-7514-49ba-a3dc-74278a53f06c/unht_a_1630236_f0006_b.jpg)
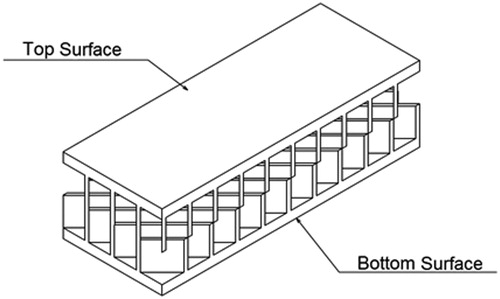
Figure 8. Temperature distribution for (a) top surface and (b) bottom surface of matrix geometry in stationary state.

Figure 9. Variation of Nu number ratio as function of dimensionless width in each sub-channel for (a) top surface and (b) bottom surface of matrix geometry in stationary state.
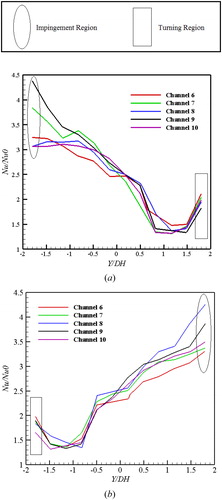
Figure 13. Temperature distribution contours in the Rotary rectangular channel with matrix geometry for (a) top surface and (b) bottom surface.

Figure 14. Variation of Nu number ratio as function of dimensionless width in each sub-channels for (a) top surface and (b) bottom surface of matrix geometry in rotary state.
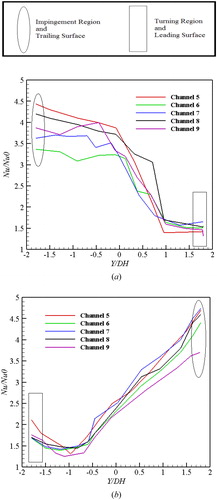
Figure 15. Variation of Nu number ratio as function of rotation number for various Reynolds number in (a) top surface and (b) bottom surface of matrix geometry in rotary state.
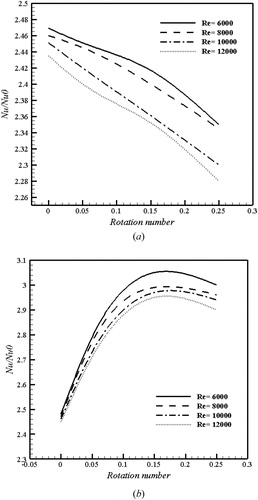
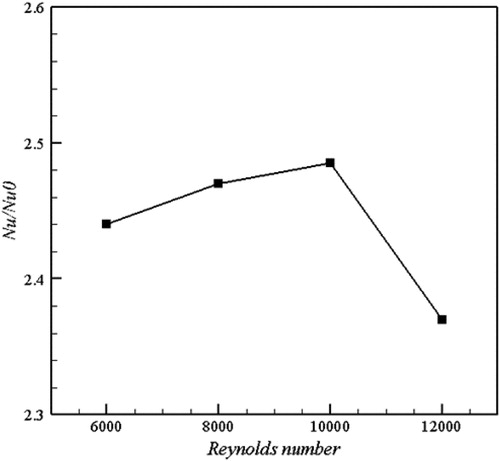
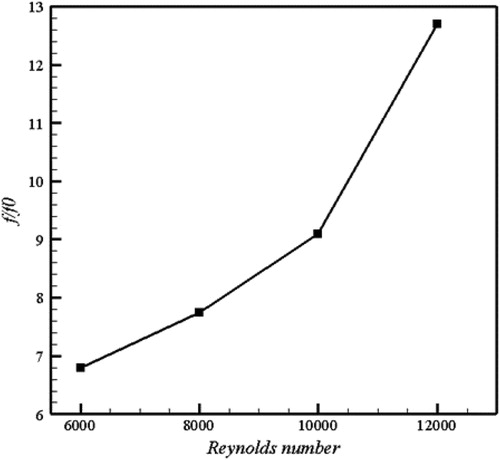
Figure 16. Variation of friction factor ratio as function of Reynolds number for various rotation numbers in the middle region of two surfaces.
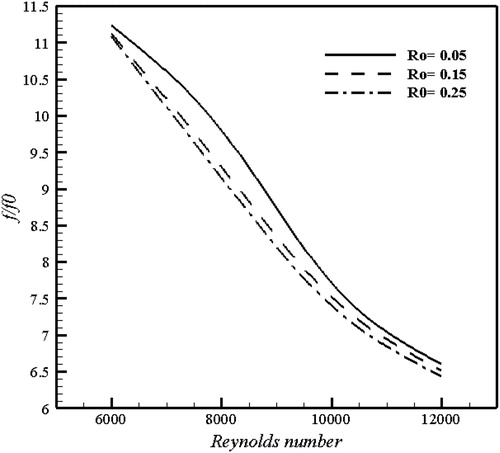
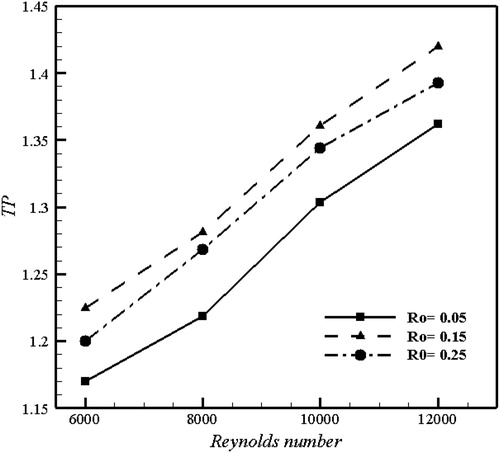
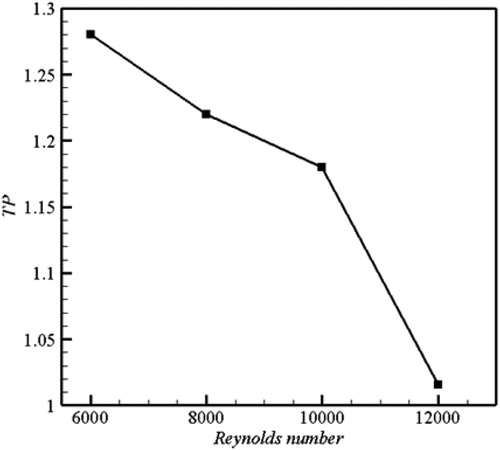
Figure 17. Variation of thermal performance as function of Reynolds number for various rotation number in the middle region of two surfaces.