Figures & data
Figure 1 A boxplot's upper whisker extends to the largest data point within 1.5 interquartile ranges. Similarly, a hungry dog will settle for the largest bone its lead will allow it to reach. Here, data points beyond the third quartile are represented as a series of increasingly large bones, while the whisker is represented as the dog's elastic lead.
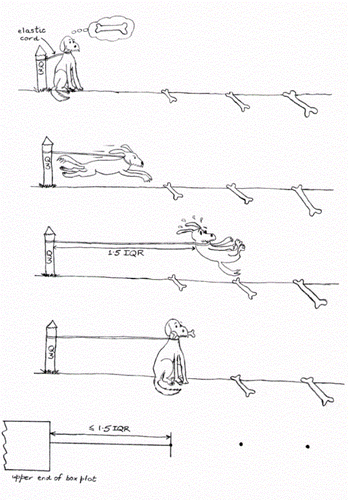
Figure 2 Expectation as child's play! A distribution sitting atop a seesaw (bottom picture) must obey the same law of physical balance as the children sitting atop the seesaw in the top part of the figure.
Figure 3 Estimation Analogy – Shooting Arrows at a target.
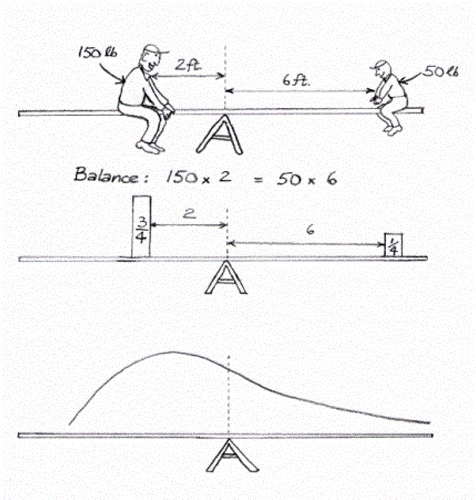
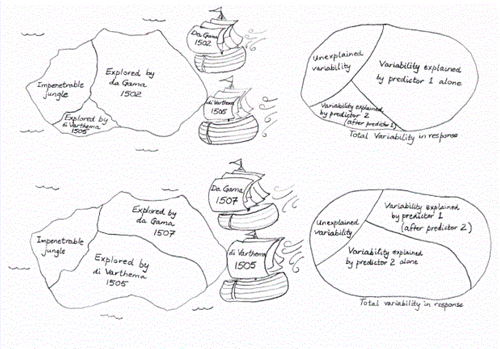
Figure 4 An analogy for sequential sums of squares. Who is credited with exploring what parts of the island depends critically on who arrived first. In the top left of the figure, DaGama claims the lion's share, having arrived in 1502, while di Varthema must settle for what's left on his arrival in 1505. Had di Varthema arrived first in 1505 (bottom left), he may have fared significantly better, while DaGama would have to settle for a much smaller portion were he to arrive later, in 1507. Analogously, variables fit first in a model can claim a larger sum of squares than if they were fit after other variables, when they would be competing for a reduced available sum of squares. In either case, regardless of the order of arrival (fit), the amount remaining unexplored (unexplained) is unchanged.
