The Challenge of Generating Causal Hypotheses Using Network Models

Figures & data

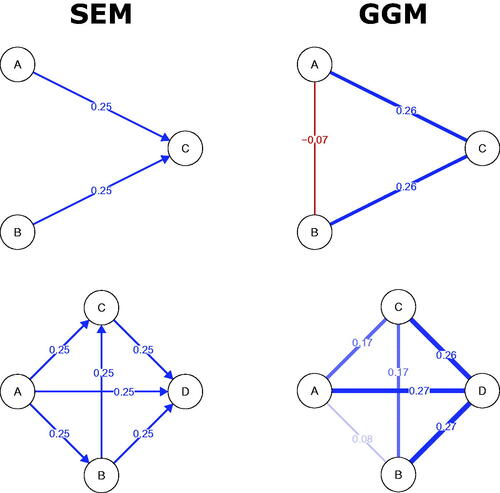
Figure 1. Four different types of network (graphical model), all describing different characteristics of the same system. Panel (a) depicts the Pairwise Markov Random Field (PMRF), panel (b) Gaussian Graphical Model (GGM), (c) Directed Acyclic Graph (DAG) and (d) a linear Structural Equation Model (SEM). In the weighted graphs, red edges depict negative relationships, blue edges depict positive edges, and the width of the edge is determined by the absolute value of the relationship (partial correlations for the GGM and regression weights for the SEM).

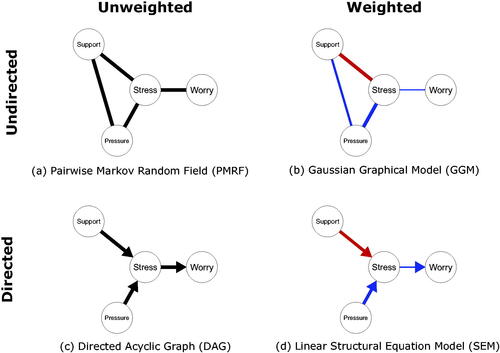
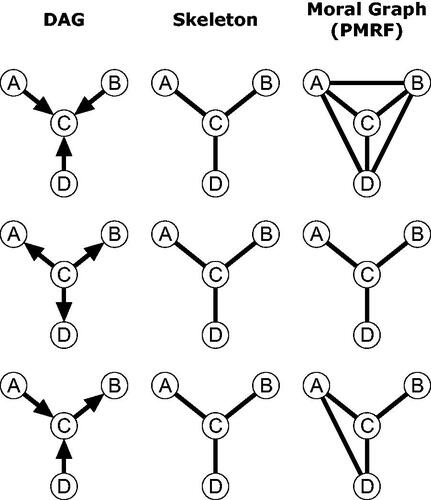
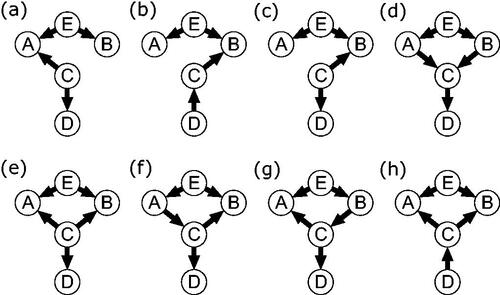
Figure 2. Visualization of the moral-equivalence set: A Pairwise Markov Random Field (PMRF) and the set of sufficient and faithful DAGs which generate that PMRF.

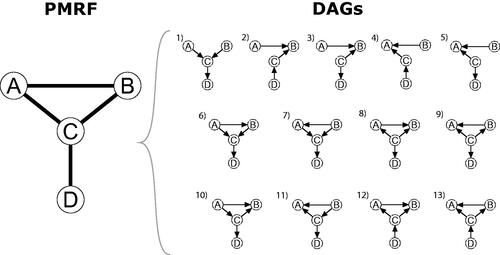
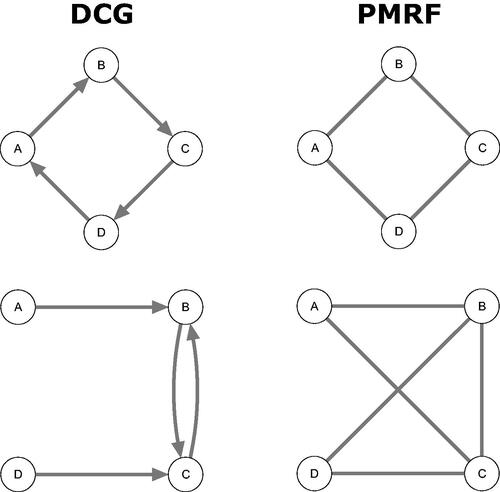
Figure 3. Four DAGs which generate the same PMRF between the variables A, B, C, and D, as shown in Figure 2, but which violate some assumption which is made in deriving the moral-equivalence set. The DAGs in (a–c) represent sufficiency violations, with unobserved common cause(s) (E and F). The linear SEM in (d) violates faithfulness, as the directed positive relationship between B and D is exactly canceled out by conditioning on C.

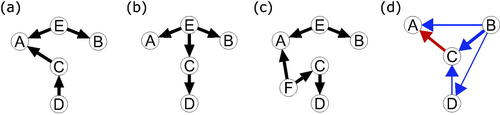
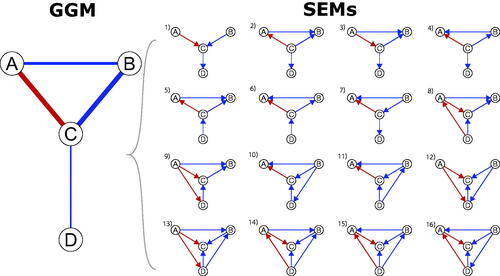
Figure 4. A Gaussian graphical model (GGM) and the set of linear SEM models which generate that GGM.

Figure 5. Three examples of DAGs which all have the same skeleton, but result in different moral graphs depending on the orientation of the edges in the DAG.

Figure 6. Two examples of linear SEMs and their corresponding GGM.

Figure 7. Two examples of directed cyclic graphs (DCGs) and their corresponding PMRF.

Figure 8. Eight additional DAGs which generate the same PMRF between the variables A–D (as shown in Figure 2). For each DAG, the set of variables A–D violates the sufficiency assumption, with respect to the variable E, a common cause of both A and B.