The rate of cellular hydrogen peroxide removal shows dependency on GSH: Mathematical insight into in vivo H₂O₂ and GPx concentrations

Figures & data

Figure 1.  The hydrogen peroxide-removal system. There are at least three principal nodes for the removal of H₂O₂. Glutathione peroxidase (GPx) is a selenoenzyme that reduces H₂O₂ to 2H₂O gathering the needed reducing equivalents from glutathione (GSH). The peroxiredoxin (Prx) family of enzymes is a separate node, removing H₂O₂ using reducing equivalents principally from thioredoxin (Trx). Catalase (CAT) is primarily located in peroxisomes; it requires no reducing cofactors to catalyse the disproportionation of H₂O₂.

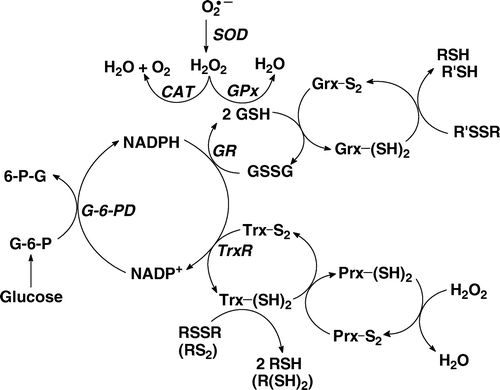
Table I.  Rate constants for modeling the kinetic behaviour of GPx [30].

Rate constant	(m^−1s^−1)
k1	2.1×10^7
k2	4×10^4
k3	1×10^7

Figure 2.  The rate of tumour growth in vivo varies directly with effective GPx activity (i.e. GPx×GSH); H₂O₂ varies inversely. (♦) Tumour volume, which is proportional to the growth rate. (□) Relative levels of intracellular H₂O₂ were estimated by monitoring the increase in fluorescence of 2′,7′-dichlorodihydrofluorescein (DCFH₂). Effective GPx activity is ‘GPx-activity’ (or GPx) as measured by standard activity assay [44] multiplied by the concentration of GSH. The units are somewhat arbitrary (AU); using typical expressions of the activity of GPx (mU/mg protein) and for GSH levels (nmol/mg protein) units for effective GPx activity would be mU?nmol (mg protein)⁻². Figure adapted from [55].

Table II.  Initial concentrations used for the GPx model.

Species	Initial concentration (m)
GSH	1×10^−4, 2×10^−4, 4×10^−4, 6×10^−4
GPxr	1×10^−7, 5×10^−7, 1×10^−6, 5×10^−6, 1×10^−5, 5×10^−5
H2O2	1×10^−7, 5×10^−7, 1×10^−6, 5×10^−6, 1×10^−5, 5×10^−5
GPxo	0
GS-GPx	0
GSSG	0

Figure 3.  Model results in determining linear dependency of time constant with respect to effective GPx activity. The dependence of the time constant, τ, on effective GPx activity, approximated by [GPx_r]₀[GSH]₀, are shown on log-log plots for various initial concentrations of GPx_r and H₂O₂. Results from the general model are shown as solid lines; results from the classical model are shown as dotted lines. The short segments result from calculations of effective GPx activity for a fixed [GPx_r]₀ with a span on [GSH]₀ (0.1, 0.2, 0.4 and 0.6 mM). If the line segments are parallel to the abscissa, then there is no dependence of τ on [GSH] in the range of concentrations tested; if the line-segments show a non-zero slope, then there is dependence of [GSH]. The system would be completely dependent on effective GPx activity if all points fell on a single straight line. [GPx_r]₀ used for both models are 0.1 µm, 0.5 µm, 1 µm, 5 µm, 10 µm and 50 µm. (a) [H₂O₂]₀  =  0.1 µm; (b) [H₂O₂]₀=0.5 µm; (c) [H₂O₂]₀=1 µm; (d) [H₂O₂]₀  =  5 µm; (e) [H₂O₂]₀=10 µm; (f) [H₂O₂]₀=50 µm. The general model captures dependency when [H₂O₂]₀ is 5 µm and [GPx_r]₀ is ≤1 µm. Note that the classical model under-predicts the [H₂O₂]₀ for the onset of effective GPx activity dependency. Furthermore, the estimated time constants for the classical model can be orders of magnitude different than that determined from the more general kinetic model.

Figure 4.  Example cases demonstrating deviations between the generalized and classical model results. Cases used here, as examples to demonstrate discrepancies, are for initial concentration of H₂O₂, [H₂O₂]₀, of 5 µm and initial concentration of GSH, [GSH]₀, of 0.1 mm. (A) Transient H₂O₂ profiles for various [GPx_r]₀ of the general (solid lines) and classical (dotted lines) models are shown in this semi-log plot. Even for cases with lower [GPx_r]₀, where the time needed for 63% decay (time constants, τ) from both models agree well, the classical model is not a good approximation throughout. For example, in the case where [GPx_r]₀ is 1 µm (magenta), the time taken for 10% decay given by both models are a factor of 10 different. (b) The rates of disappearance of H₂O₂ for various [GPx_r]₀ of the general (solid lines) and classical (dotted lines) models are plotted with a semi-log scale. Using the same case of where [GPx_r]₀ is 1 µm (magenta), at physiological turnover time for H₂O₂ of ms, the rate of removal of H₂O₂ given by the general model is approximately a factor of 100 greater than the classical rate.

Figure 5.  Example of the rate-limiting effect of the slower GPx_r recycling step. Concentration profiles of H₂O₂ and GPx_r of the general model are shown for [H₂O₂]₀ of 5 µm, [GSH]₀ of 0.1 mM and [GPx_r]₀ of 1 µm. The inflection point on the [H₂O₂]-profile that occurs around 40 ms corresponds to the change in the rate of production of GPx_r.

Antunes F, Salvador A, Pinto RE. PHGPx and phospholipase A2/GPx: comparative importance on the reduction of hydroperoxides in rat liver mitochondria. Free Radic Biol Med 1995; 19: 669–677

 PubMed Web of Science ®Google Scholar

Oberley LW, Buettner GR. The role of superoxide dismutase in cancer: a review. Cancer Res 1979; 39: 1141–1149

 PubMed Web of Science ®Google Scholar

Li, SJ. The role of cellular glutathione peroxidase redox regulation in the suppression of tumor cell growth by managanese superoxide dismutase [dissertation]. Iowa City, IA: University of Iowa; 1999. Available from The University of Iowa, Iowa City, IA.

 Google Scholar