3D DDD modelling of dislocation–precipitate interaction in a nickel-based single crystal superalloy under cyclic deformation

Figures & data

Figure 1. (colour online) RVEs with (a) 1, (b) 8 and (c) 27 precipitates, where initial Frank-Read dislocation sources are randomly distributed in the -phase matrix.

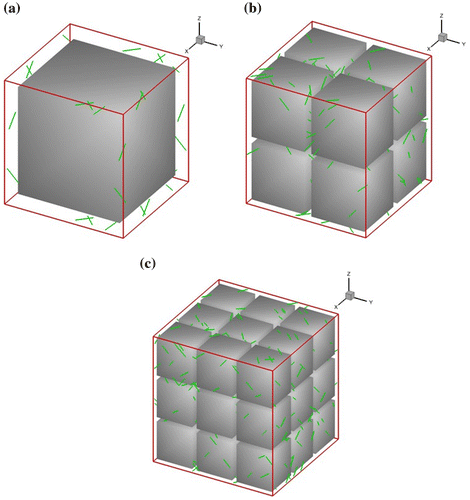
Figure 2. (colour online) Stress–strain response for RVEs with different number of precipitates for (a) [0 0 1] orientation; (b) [1 1 1] orientation.

Figure 3. (colour online) Dislocation density against time for RVEs with different number of precipitates for (a) [0 0 1] orientation; (b) [1 1 1] orientation.

Table 1. The parameters used in 3D DDD simulations.

Orientation	[0 0 1]	[1 1 1]
Young’s modulus (GPa)	99.3	247.3
Poisson ratio	0.402	0.24
APB energy (mJ/m^2)	150
Drag coefficient (Pa s)	1.0e–4
KW unlocking stress (MPa)	425
Friction stress in γ phase (MPa)	180

Figure 4. (colour online) Cyclic stress–strain response simulated with 3D DDD model at for (a) [0 0 1] and (b) [1 1 1] orientations.

Figure 5. (colour online) Dislocation networks for [0 0 1] orientation at (a) time = 1 s, (b) time = 4 s, (c) time = 5 s, (d) time = 8 s and (e) time = 9 s.

Figure 6. (colour online) Dislocation networks for [1 1 1] orientation at (a) time = 1 s, (b) time = 4 s, (c) time = 5 s, (d) time = 8 s and (e) time = 9 s.

Figure 7. (colour online) Maximum-shear plastic strain contour at strain = 1% for (a) [0 0 1] and (b) [1 1 1] orientations.

Figure 8. (colour online) Stress–strain response with and without precipitate for (a) [0 0 1] and (b) [1 1 1] orientations.

Figure 9. (colour online) Stress–strain response with and without shearing of precipitate by dislocations for (a) [0 0 1] and (b) [1 1 1] orientations.

Figure 10. (colour online) Shearing of dislocations into precipitate for [0 0 1] orientation at: (a) strain = 1% and (b) strain = 2%.

Figure 11. (colour online) Shearing of dislocations into precipitate for [1 1 1] orientation at: (a) strain = 1% and (b) strain = 2%.

Figure 12. (colour online) Evolution of the dislocation density: (a) simulations in this work for both [0 0 1] and [1 1 1] orientations and (b) the in situ measurements by Huang et al. [34].

Figure 13. (colour online) (a) Evolution of dislocation density; dislocation networks at the end of the first (b) and the fifth (c) cycles for [0 0 1] orientation.

Figure 14. (colour online) (a) Evolution of dislocation density; dislocation networks at the end of the first (b) and the fifth (c) cycles for [1 1 1] orientation.

E.W. Huang, R.I. Barabash, Y.D. Wang, B. Clausen, L. Li, P.K. Liaw, G.E. Ice, Y. Ren, H. Choo, L.M. Pike, and D.L. Klarstrom, Plastic behavior of a nickel-based alloy under monotonic-tension and low-cycle-fatigue loading, Int. J. Plast. 24 (2008), pp. 1440–1456.10.1016/j.ijplas.2007.10.001

 Web of Science ®Google Scholar