On the sparsity of synthetic control method

Figures & data

Figure 1. Multiple exact solutions.

Figure 2. A unique exact solution.

Figure 3. A unique approximate solution on an edge.

Figure 4. A unique approximate solution on a vertex.

Figure 5. Approximate solutions that are not unique.

Table 1. A case study of California’s tobacco control program.

$\mathit{N}$	$\mathit{K}$	$N_p$	$N_z$	Covariates
38	1	38	0	retprice
38	2	2	36	retprice, lnincome
38	3	3	35	retprice, lnincome, age15to24
38	4	4	34	retprice, lnincome, age15to24, beer
38	5	5	33	retprice, lnincome, age15to24, beer, cigsale(1975)
38	6	4	34	retprice, lnincome, age15to24, beer, cigsale(1975), cigsale(1980)
38	7	4	34	retprice, lnincome, age15to24, beer, cigsale(1975), cigsale(1980), cigsale(1988)

For variable definitions, refer to Abadie et al. (2010).

Figure 6. Optimal synthetic control in the 2D parameter space.

Figure 7. Optimal synthetic control in the 3D parameter space.

Table 2. Summary statistics.

Variable	Observations	Mean	Std. Dev.	Min	Max
$\mathit{N}$	658	26.588	23.975	4	326
$\mathit{K}$	658	9.336	4.479	3	27
$\mathit{K}/\mathit{N}$	658	0.522	0.369	0.0215	3.25
$N_p$	658	5.784	6.491	1	54
$N_z$	658	20.792	23.959	0	319
sparsity ($N_z/\mathit{N}$)	658	0.698	0.257	0	0.991

Figure 8. The distribution of sparsity.

Figure 9. The numbers of positive weights and covariates.

Figure 10. The number of positive weights and the number of covariates.

Table 3. Results of OLS regressions.

Dependent Variable: sparsity	(1)	(2)	(3)	(4)
$\mathit{K}/\mathit{N}$	−0.243**	−0.238***	−0.258***	−0.224***
	(0.0937)	(0.0855)	(0.0902)	(0.0705)
$\mathit{K}$	0.0228	0.0199	0.0175
	(0.0183)	(0.0137)	(0.0134)
$\mathit{N}$	0.00285	0.00199
	(0.00332)	(0.00172)
$\mathit{K}\times \mathit{N}$	−0.000126
	(0.000320)
constant	0.762***	0.783***	0.859***	1.043***
	(0.161)	(0.134)	(0.106)	(0.0529)
paper fixed effects	Yes	Yes	Yes	Yes
N	658	658	658	658
R^2	0.571	0.571	0.570	0.567
Adjusted R^2	0.485	0.486	0.486	0.483

Standard errors clustered at the paper level are in parentheses.

*p < 0.1, **p < 0.05, ***p < 0.01.

Table 4. Results of fractional probit regressions.

Dependent Variable: sparsity	(1)	(2)	(3)	(4)
$\mathit{K}/\mathit{N}$	−0.804**	−0.786***	−0.867***	−0.744***
	(0.320)	(0.283)	(0.306)	(0.223)
$\mathit{K}$	0.0700	0.0618	0.0572
	(0.0574)	(0.0423)	(0.0433)
$\mathit{N}$	0.00884	0.00645
	(0.0100)	(0.00494)
$\mathit{K}\times \mathit{N}$	−0.000377
	(0.00116)
constant	0.844*	0.895**	1.115***	1.708***
	(0.441)	(0.371)	(0.331)	(0.167)
paper fixed effects	Yes	Yes	Yes	Yes
N	658	658	658	658
Pseudo R^2	0.151	0.151	0.151	0.150

Standard errors clustered at the paper level are in parentheses.

*p < 0.1, **p < 0.05, ***p < 0.01.

Table 5. Results of fractional logit regressions.

Dependent Variable: sparsity	(1)	(2)	(3)	(4)
$\mathit{K}/\mathit{N}$	−1.276**	−1.257***	−1.405***	−1.217***
	(0.537)	(0.469)	(0.519)	(0.373)
$\mathit{K}$	0.108	0.100	0.0937
	(0.100)	(0.0736)	(0.0758)
$\mathit{N}$	0.0144	0.0120
	(0.0192)	(0.00967)
$\mathit{K}\times \mathit{N}$	−0.000400
	(0.00227)
constant	1.449*	1.495**	1.876***	2.859***
	(0.781)	(0.674)	(0.589)	(0.280)
paper fixed effects	Yes	Yes	Yes	Yes
N	658	658	658	658
Pseudo R^2	0.151	0.151	0.150	0.150

Standard errors clustered at the paper level are in parentheses.

*p < 0.1, **p < 0.05, ***p < 0.01.

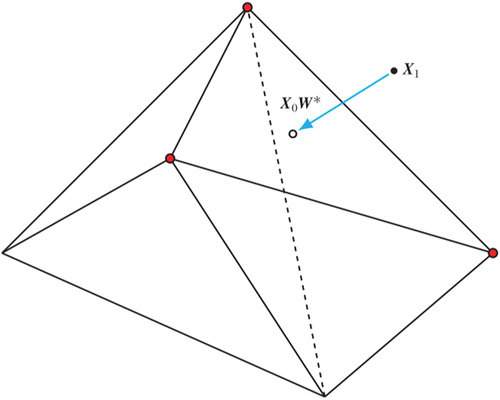
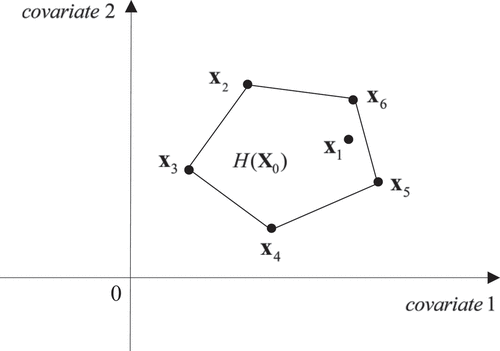
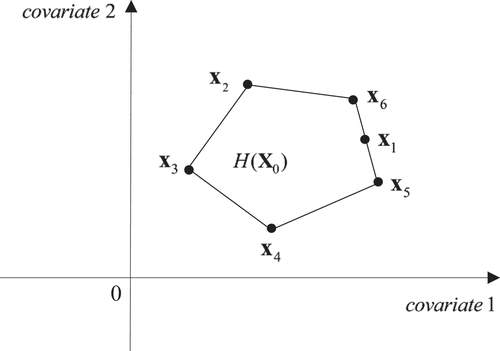
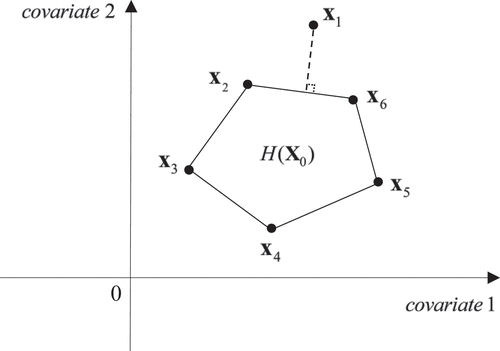
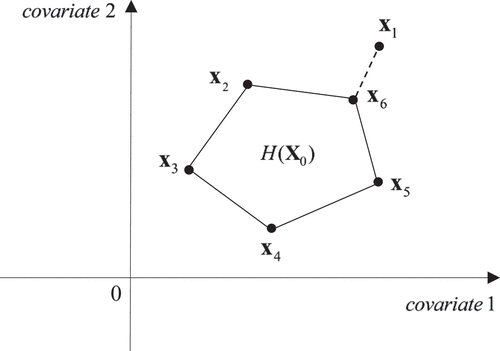
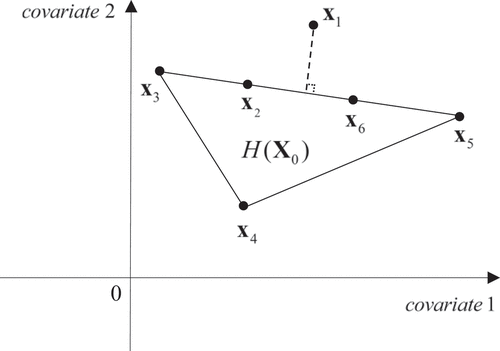
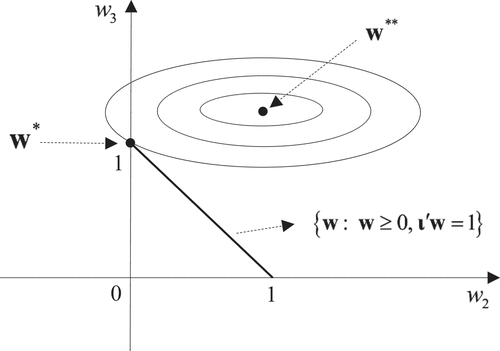
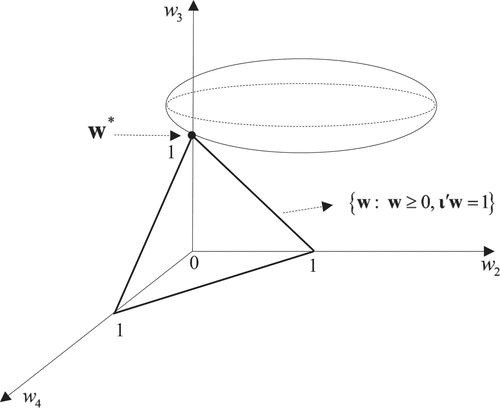
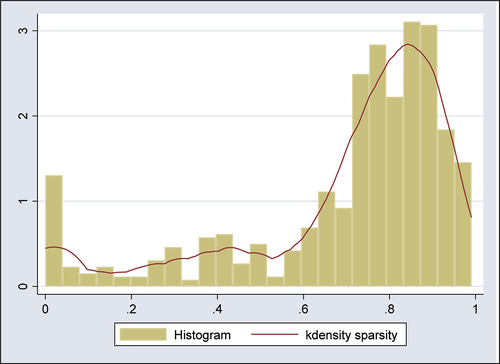
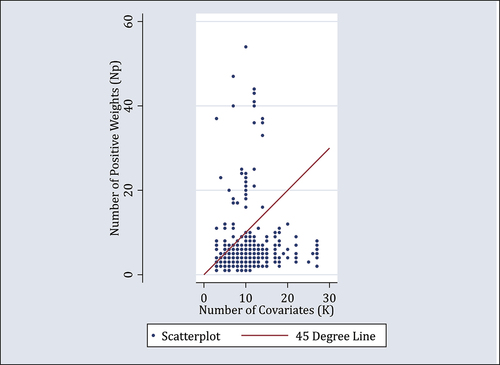
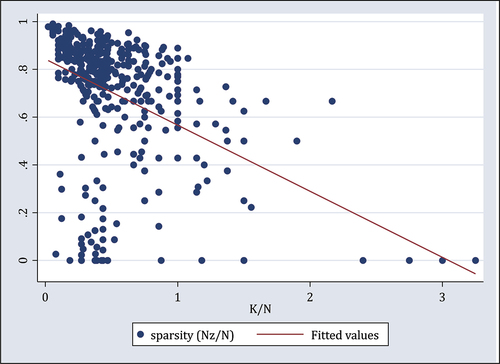
Figure A1. Projecting $X_1$ on the convex hull of $X_0$.

Figure A1 in Abadie (2021) is reproduced here for convenience.

Abadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American Statistical Association, 105(490), 493–505. https://doi.org/10.1198/jasa.2009.ap08746

 Web of Science ®Google Scholar

Abadie, A. (2021). Using synthetic controls: Feasibility, data requirements, and methodological aspects. Journal of Economic Literature, 59(2), 391–20. https://doi.org/10.1257/jel.20191450

 Web of Science ®Google Scholar