Accounting deviations between the measured and simulated impact pressures in high-density snow avalanches

Figures & data

Table 1. Summary of the research work carried out by various authors for the estimation of snow avalanche impact pressures.

Bibliographic reference	Scale of study	Avalanche regime	Shape of the obstacle	Formula for calculating avalanche impact pressure, Ps (kPa)/Other details	Range of estimated values	Type of model
Furukawa (1957)	Small-scale	Blocks of snow released on an inclined plane (experiments)	Instrumented catch dam type	$P_s=35{\left(1.35\frac{v_s^2}{\mathit{g}}{{\rho }_i}^{1.5}\right)}^{0.45}$, here vs is velocity of snow (m·s^−1), ρi is density of snow before impact on the obstacle (gm·cm^−3), g =9.81 m·s^−2	10 to 130 kPa (experimental)	Empirical
Pedersen, Dent, and Lang (1979)	Small-scale	Snow as Newtonian fluid (model)	0.6 m high rectangular obstacle	Normal impact force Fn on the obstacle given in Newtons as: $F_n=0.2{\rho }_i{v}_s^2\left(\frac{16R}{v_s^{0.25}}-1\right)$, here, R is the ratio of obstacle height and the avalanche depth, vs is the velocity of snow (m·s^−1), ρi is the density of snow before impact on the obstacle (kg·m^−3)	190 to 520 m^2 ·s^−2 (impact pressure per unit snow density) as per model and 150 to 400 m^2 ·s^−2 as per experiments	2-D numerical model solving Navier-Stokes (N-S) equations and the analytical model (SMAC)
Lang and Dent (1980)	Small-scale (2.5 m long and 0.3 m wide track)	Snow as Newtonian fluid (model)	Instrumented rectangular obstacle (0.3 m wide and 0.05 m high, made of balsa wood)	Compared the measured and simulated impact forces and found in agreement with each other.	9.8 N to 15.5 N (model) and 11.0 N to 14.5 N (experiments)	2-D numerical model solving Navier-Stokes (N-S) equations (AVALNCH)
Mead et al. (1986)	Small-scale	Snow as Newtonian fluid and bi-viscous Bingham fluid (model) and snow-blocks (experiments)	Instrumented vertical barrier consisting of 12 panels each 1.0 m wide and 0.3 m high mounted on two horizontal load cells	Agreement found between the measured snow-block impulse force against the vertical barriers and the model results. Kinematic viscosity was found the most important parameter in the model.	240 to 400 N·s (model) and 275 to 475 N·s (experiments)	2-D numerical model solving Navier-Stokes (N-S) equations (SMAC)
Nakamura et al. (1987)	Snow chute (25 m long, 1 m wide, and slope fixed at 30^°)	Natural and sintered snow	0.823 m high instrumented post with six load cells	$P_s\left(\mathit{normal}\mathit{impact}\right)={\rho }_i{v}_s^2$ $P_s\left(\mathit{plastic}\mathit{wave}\mathit{theory}\right)={\rho }_i{v}_s^2\left(1+\frac{{\rho }_i}{{\rho }_{\mathit{f}}-{\rho }_i}\right)$, ρf is density of snow after impact on the obstacle (kg·m^−3)	45 to 203 kPa (model) and 161 to 358 kPa (experiments)	Analytical
Eglit, Kulibaba, and Naaim (2007)	Small-scale	Low-density and high-density avalanches (model)	Arbitrary vertical obstacle perpendicular to the flow	$P_s=\frac{{\rho }_f}{{\rho }_{\mathit{f}}-{\rho }_i}{\rho }_i{v}_s^2$	Ratio of pressure behind the shock to that of pressure in front of the shock for dense avalanches varied from 1.0 to 1.5 (model)	Analytical
Hauksson et al. (2007)	Snow chute (7.5 m long and 0.35 m wide)	Glass beads with mean particle size 90 μm, and bulk density ≈ 1500 kg·m^−3	Rectangular and cylindrical obstacles of varying dimensions	No formula given	1.5 to 2.8 N (cylindrical obstacles) and 2.0 to 9.2 N (rectangular obstacles)	No model
Oda et al. (2011)	Snow chute (8 m long and 0.8 m wide)	Snow with density range 50 to 300 kg·m^−3 (experiments) and Bingham fluid (model)	Instrumented rectangular obstacle of height 0.6 m and width 0.75 m	No formula given	500 to 1500 N (model) and 500 to 900 N (experiments)	2-D two-phase model of snow and air solving N-S equations
Aggarwal and Kumar (2012)	Snow chute (61 m long and 2 m wide)	Snow with density range 240 to 330 kg·m^−3 (experiments) and bi-viscous Bingham fluid (model)	Rectangular obstacles of height varying from 0.62 m to 1.0 m	No formula given	16 kPa (model)	2-D two-phase model of snow and air solving N-S equations
Salway (1978)	Real-scale	Dry snow avalanche (experiments)	Stand with four load cells, each having surface area of 645 mm^2.	$P_s=k_c{v}_s^2$, here kc is the coefficient estimated from the observed impact pressure and the snow velocity.	Peak values of 1000 to 1350 kPa (experiments)	Analytical
McClung and Schaerer (1985)	Real-scale	Dry and wet snow (experiments)	Five load cells, each having surface area of 645 mm^2 mounted on a 5.2 m high frame and secondly a 0.5 m diameter aluminium plate mounted on a steel frame	$P_s\left(\mathit{average}\mathit{pressures}\right)=\frac{1}{2}{C}_d^{\prime }\mathit{\rho }{v}_s^2$, here, $C_d$ is the effective drag coefficient. $P_s\left(\mathit{peak}\mathit{pressure}\right)={\rho }_i{v}_s^2\left(1+\frac{{\rho }_i}{\mathit{\rho f}-{\rho }_i}\right)$, ρf is density of snow after impact on the obstacle (kg·m^−3).	Peak values of 100 to 1160 kPa (experiments)	Analytical
Sovilla, Schaer et al. (2008)	Real-scale	Dry and wet snow (experiments)	20 m high tubular pylon instrumented with pressure transducers	$P_s=\frac{1}{2}{C}_d^{\prime }{\rho }_i{v}_s^2$, here, $C_d^{\prime }$ is the effective drag coefficient.	Peak values of 50 to 800 kPa (experiments)	Analytical
Sovilla, Schaer, and Rammer (2008)	Real-scale	Dense and powder snow (experiments)	20 m high tubular pylon and a 5 m high steel wedge	$P_s=\frac{1}{2}{C^{\prime }}_{\mathit{d}}{\rho }_i{v}_s^2$, here $C_d^{\prime }$ is taken as 2.0 corresponding to a rectangular obstacle of small dimensions and ρi =300 kg·m^−3 as per Swiss procedure.	Peak values of 100 to 1000 kPa (experiments)	Analytical
Christen, Kowalski, and Bartelt (2010)	Real-scale	Dry and wet snow (experiments)	No details given	$P_s=\frac{1}{2}{C^{\prime }}_{\mathit{d}}{\rho }_i{v}_s^2$, here $C_d^{\prime }$ was taken as 2.0 as per Swiss procedure.	Peak values of 261 to 804 kPa (model)	2-D numerical model RAMMS solving depth-averaged equations and analytical model
Faug et al. (2010)	Real-scale	Dry and cold snow (experiments)	Rectangular wall	Please refer to the paper for the proposed equations	Normalized force values ranged from 0.2 to 3.0 (model)	3-D analytical model
Baroudi, Sovilla, and Thibert (2011)	Real-scale	Dry snow and wet snow (experiments)	20 m high instrumented tower with piezoelectric and strain-gauge cantilever sensors	For wet snow avalanches, $P_s=\mathit{\zeta }{\rho }_i\mathit{gH}$, $\mathit{\zeta }$ is empirical parameter having mean value of 7.6, Heff is the avalanche flow depth with respect to the position of the sensor where the pressure is measured.	Peak pressures in the range of 200 to 800 kPa (experimental)	Empirical
Sovilla et al. (2016)	Real-scale	Wet snow (experiments)	20 m high instrumented tower with piezoelectric and strain-gauge cantilever sensors. Secondly, a 4.5 m high instrumented concrete wall used.	For wet snow avalanches, total pressure is sum of inertial and gravitational components $P_s=\frac{1}{2}{C}_d{\rho }_i{v}_s^2+\mathit{\zeta }{\rho }_i\mathit{g}\mathit{H}{}_{\mathit{eff}}$ Authors considered value of drag coefficient Cd as 3.0 and $\mathit{\zeta }$ with a mean value of 7.6.	Peak pressures in the range of 50 to 500 kPa (experimental)	Empirical
Maggioni et al. (2019)	Real-scale	Dense snow and mixed snow (experiments)	2.7 m high rectangular instrumented obstacle	No formula given	Average pressures varied from 2 to 30 kPa (experiments)	No model
Kyburz et al. (2022)	Real-scale	Snow as granular particles (model)	Rectangular, circular, and triangular geometries (model)	Based on the simulated impact pressures Ps, proposed effective snow drag coefficient, $C_d^{\prime }=C_{\mathit{geo}}\left(1+\frac{K_e}{F_r^2}\right)$, here Cgeo is the geometry dependent coefficient of $C_d^{\prime }$, Ke is the earth pressure coefficient and Fr is Froude number.	50 to 500 kPa (model)	3-D discrete element model (DEM)
Thibert et al. (2008) and Baroudi and Thibert (2009)	Real-scale	Dry and dense snow (real avalanche)	1 m^2 instrumented plate supported by a 3.5 m high steel cantilever	$P_s=C_d{\rho }_i{v}_{sf}^2$, here, $C_d^{\prime }$ is the effective drag coefficient which is considered equal to C0 Cr . The snow geometry coefficient C0 is equal to 2(1-cos). Here, is the angle of the dead zone formed upstream of the obstacle. Cr represents the flow regime contribution to the drag coefficient which is given equal to 10.8Fr^−1.3, vsf is the velocity of snow far away from the obstacle.	Peak pressure of 35 kPa (inverse analysis)	Finite element model and analytical model
Bovet et al. (2011)	Real-scale	Soft snow (real avalanche) and Newtonian fluid (model)	Houses damaged in the avalanche	$P_s=\frac{1}{2}{C}_d^{\prime }{\rho }_i{v}_s^2$, here, authors took $C_d^{\prime }$ as 2 considering square shape of the buildings and density of snow ρi as 130 kg·m^−3. This equation was used to estimate snow velocity vs from the known impact pressure value Ps from the numerical model.	Peak pressure of 18.8 to 54.5 kPa (back analysis) and 10.7 to 60 kPa (model)	2-D numerical model solving N-S equations and the analytical model
Thibert et al. (2013)	Real-scale	Moist/wet snow (real avalanche)	1 m^2 instrumented plate supported by a 3.5 m high steel cantilever	$P_s=\frac{1}{2}{C}_d^{\prime }{\rho }_i{v}_s^2$, authors used this equation to estimate $C_d^{\prime }$ from the reconstructed impact pressures Ps and the measured snow velocities vs.	2 to 12 kPa (inverse analysis)	Analytical (inverse analysis)
De Biagi, Chiaia, and Frigo (2015)	Real-scale	Soft slab (real avalanche)	Houses affected by the avalanche	$P_s={\rho }_i{v}_s^2$, authors used this equation for estimating pressures on few houses affected.	22 to 389 kPa (back analysis)	Analytical (back analysis)
Frigo et al. (2020)	Real-scale	A mixture of snow, uprooted and crushed trees, rocks etc… (real avalanche)	Hotel hit by the avalanche	$P_s={\rho }_i{v}_s^2$, here, authors used snow density ρi as estimated by the model near the impact point.	Peak pressure of 393 kPa (model)	2-D numerical model RAMMS solving depth-averaged equations (back analysis)

SMAC = Simplified Marker-and-Cell approach.

Figure 1. A view of the (a) snow chute at Dhundhi, Himachal Pradesh, India. (b) AIPMS on the test bed of the chute (at a distance of 0.9 m from the end of the 12° slope).

Figure 2. Schematic of the AIPMS showing (a) its position at a distance of 0.9 m from the end of the 12° slope of the snow chute, (b) its front plate facing the avalanche, and (c) side view showing the back support detail.

Figure 3. A view of the AIPMS installed on snow chute, Dhundhi, Himachal Pradesh, India.

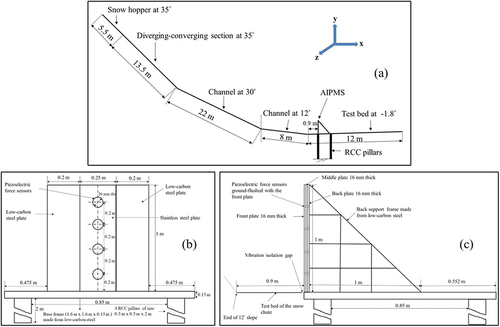
Figure 4. A view of the interaction of the snow avalanches with AIPMS at the snow chute, Dhundhi, Himachal Pradesh, India.

Figure 5. Boundary conditions for the 3D geometry of the snow chute at Dhundhi, Himachal Pradesh (Aggarwal and Kumar 2012).

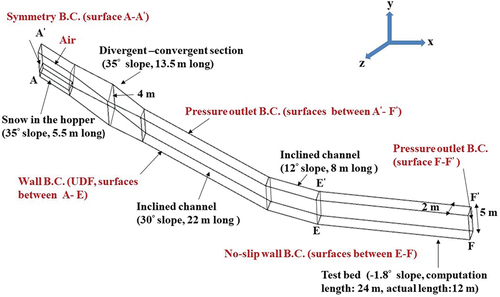
Figure 6. Wall shear stress components of snow on an inclined plane. τ_s|wall (N·m⁻²) stands for the total wall shear stress of snow, τ_s,x|wall (N·m⁻²) stands for the x-component of τ_s|wall, τ_{s, y|wall} (N·m⁻²) stands for the y-component of τ_s|wall, and θ (°) is the angle of the plane.

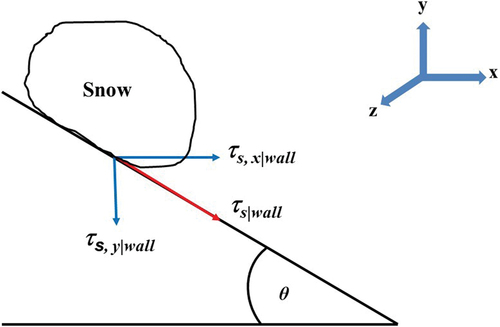
Figure 7. Flow rheology of snow as a bi-viscous Bingham fluid. τ₀ (N·m⁻²) stands for the yield strength of snow, ${\eta }_0$ (N·s·m⁻²) stands for the dynamic viscosity of snow in the locked portion of the flow, k (N·s·m⁻²) stands for the dynamic viscosity of snow after the yield region, and ${\dot{\gamma }}_0$ (s⁻¹) stands for the shear strain rate of snow in the locked portion of the flow.

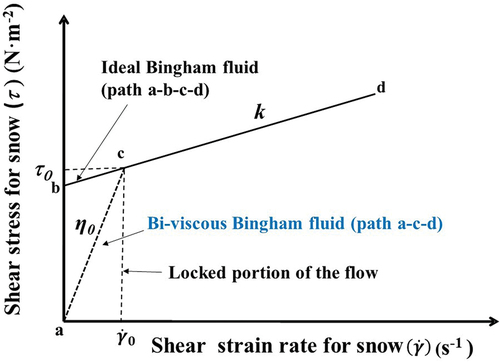
Figure 8. Contours of snow velocity v_S at a timestep t = 1.5 seconds, after the release of 11 m³ of snow of density ρ_i = 582 kg·m⁻³ from the hopper of the snow chute, Dhundhi, Himachal Pradesh, India, for the varying mesh sizes of (a) 0.05 m, (b) 0.1 m, and (c) 0.2 m (15 March 2021; experiment E2).

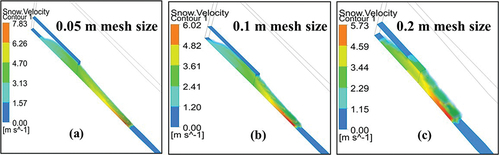
Table 2. Effect of the mesh size on the model simulations.

Mesh size (m)	Maximum aspect ratio	Minimum orthogonal quality	Number of cells	Time taken to complete 1.5-second simulation (hours)	Estimated time taken to complete the full simulation (hours)	Simulated max. snow velocity vs,max at t = 1.5 seconds (m· s^−1)
0.025	Memory allocation error while generating the mesh
0.050	3.3220	0.8106	5,792,000	60.39	322.09	7.83
0.10	3.3205	0.8110	724,000	1.54	8.22	6.02
0.20	3.3169	0.8118	90,750	0.60	3.20	5.73

Table 3. Summary of the experiments for the measurement of avalanche impact pressure P_m at the snow chute, Dhundhi, Himachal Pradesh, India.

Date of experiment	Volume of snow in the hopper, V (m^3)	Average density of snow in the hopper, ρi (kg·m^−3)	Average density of snow near AIPMS after hitting, ρf (kg ·m^−3)	Types of snow grains	ISCG^a code	Liquid water content in the snow	Average temperature of snow, Ts (°C)	Natural/sieved snow
14 February 2020	11	325	445	Rounded grains	RGlr	M	−1.0	Natural
17 February 2020	11	415	550	Melt forms	MFcl	M	−0.5	Natural
23 February 2020	11	445	545	Melt forms	MFcl	M	−0.5	Natural
15 March 2021 (E1)	11	578	635	Melt forms	MFcl	M	0.2	Natural
15 March 2021 (E2)	11	582	640	Melt forms	MFcl	M	0.2	Natural
18 March 2021	11	565	602	Melt forms	MFcl	M	−0.3	Natural
19 March 2021	11	542	576	Melt forms	MFcl	M	0.4	Natural

Note: ^aThe International Classification for Seasonal Snow on the Ground (Fierz et al. 2009).

Figure 9. Variation of simulated Reynolds number R_e and Froude number F_r of the flowing snow shown as a function of time t, just after the snow is released from the hopper of the snow chute, Dhundhi, Himachal Pradesh, India, for the demonstration of the dynamic behavior of the chute avalanches versus real avalanches.

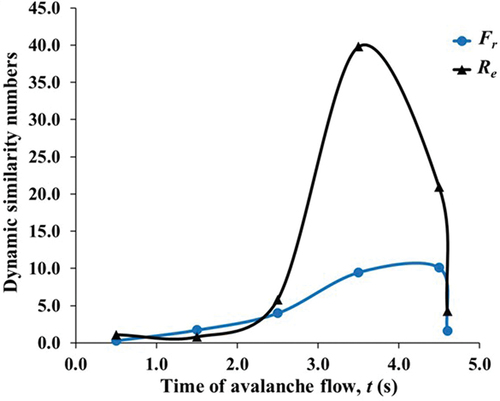
Figure 10. Simulation results of experiment on 17 February 2020 for avalanche flow mass and its interaction with AIPMS at various timesteps t of the flow.

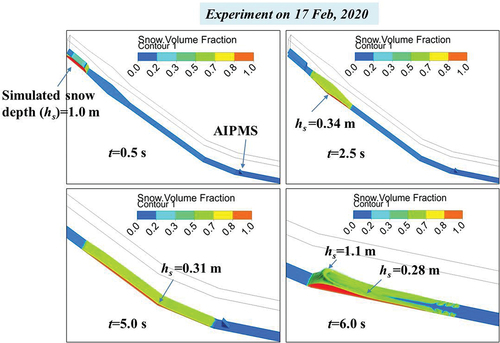
Figure 11. At a timestep t =5.2 s, simulated (a) snow velocity v_s and (b) snow total pressure (impact pressure) P_s (17 February 2020).

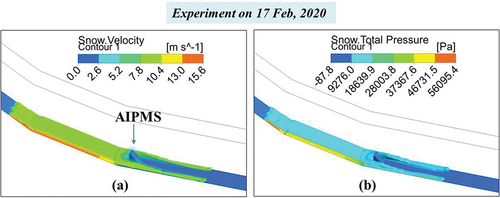
Figure 12. Observation of the avalanche flow and its depth at the significant points on the snow chute at various flow timesteps t during the experiment carried out on 17 February 2020.

Figure 13. Simulated versus measured avalanche impact pressures at (a) 0.2-m and (b) 0.6-m depth from the snow chute test bed surface (14 February 2020, 17 February 2020, and 23 February 2020).

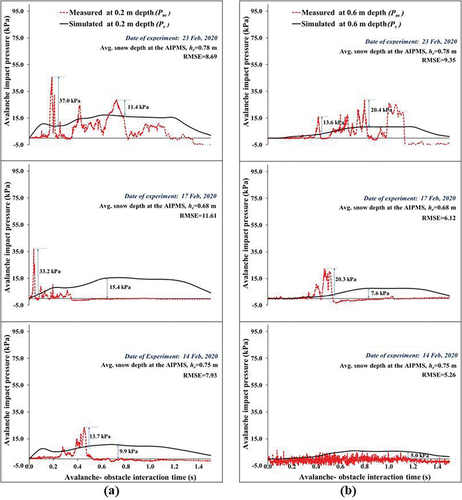
Figure 14. Simulated versus measured avalanche impact pressures at (a) 0.2-m depth and (b) 0.6-m depth from the snow chute test bed surface (15 March 2021, experiment E1; 18 March 2021; and 19 March 2021).

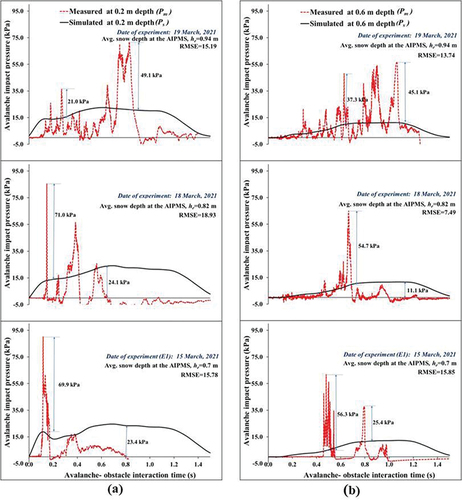
Table 4. Ratio R_p of the peak values of the measured avalanche impact pressures P_m,max and simulated avalanche impact pressures P_s,max.

Sr. no.	Average density of snow before impact, ρi (kg· m^−3)	Peak value of the simulated impact pressure, Ps,max (kPa)	Peak value of the measured impact pressure, Pm,max (kPa)	$\mathrm{Ratio}{R}_p=\frac{\mathit{P}{\mathit{ }}_{\mathit{m},\mathit{max}}}{\mathit{P}{ }_{\mathit{s},\mathit{max}}}$
1.	325	10.77	23.60	2.19
2.	415	15.45	37.20	2.41
3.	445	17.23	46.00	2.67
4.	542	22.59	71.90	3.18
5.	565	24.20	84.90	3.51
6.	578	24.57	90.26	3.67

Figure 15. Measurement of the avalanche impact pressures P_m by AIPMS after complete blocking of the avalanche flow from the sides with barriers (15 March 2021, experiment E2).

Figure 16. Simulated versus measured avalanche impact pressures after complete blocking of flow from the sides with the barriers at (a) 0.2-m depth and (b) 0.6-m depth from the snow chute test bed surface (15 March 2021, experiment E2).

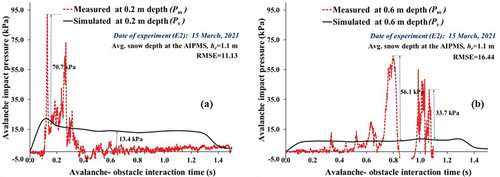
Figure 17. Variation of simulated fluid drag coefficient C_d and the corresponding effective drag coefficient $C_d^{\prime }$ during the avalanche flow–obstacle interaction process for experiments conducted on (a) 15 March 2021 (experiment E1, ρ_i = 578 kg·m⁻³) and (b) 14 February 2020 (ρ_i = 325 kg·m⁻³).

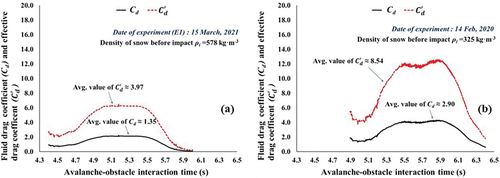
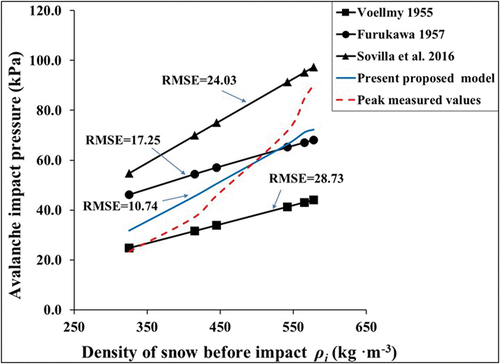
Figure 18. Comparison of deviations between the output of the proposed model P_i and other well-known models for the estimation of peak avalanche impact pressures on the obstacles. Deviations for the above models were calculated with reference to the peak measured avalanche impact pressures P_m,max in the current experiments.

Furukawa, I. 1957. Impact of avalanche. Journal of the Japanese Society of Snow and Ice 19 no, 5: 140–1. doi:10.5331/seppyo.19.140.

 Google Scholar

Pedersen, R. R., J. D. Dent, and T. E. Lang. 1979. Forces on structures impacted and enveloped by avalanches. Journal of Glaciology 22, no. 88: 529–34. doi:10.3189/S0022143000014507.

 Google Scholar

Lang, T. E., and J. D. Dent. 1980. Scale modeling of snow-avalanche impact on structures. Journal of Glaciology 26, no. 94: 189–96. doi:10.3189/S0022143000010728.

 Web of Science ®Google Scholar

Mead, L. B., H. Nakamura, T. E. Lang, and J. D. Dent. 1986. Comparison of experimental and computer modeling of snow-block impact on structures. Journal of Glaciology 32, no. 112: 321–4. doi:10.3189/S0022143000011989.

 Web of Science ®Google Scholar

Nakamura, T. 1987. A newly designed chute for snow avalanche experiments. International Association of Hydrological Sciences (IAHS) Publication 162: 441–51.

 Google Scholar

Eglit, M. E., V. S. Kulibaba, and M. Naaim. 2007. Impact of a snow avalanche against an obstacle: Formation of shock waves. Cold Regions Science and Technology 50, no. 1–3: 86–96. doi:10.1016/j.coldregions.2007.06.005.

 Web of Science ®Google Scholar

Hauksson, S., M. Pagliardi, M. Barbolini, and T. Johannesson. 2007. Laboratory measurements of impact forces of supercritical granular flow against mast-like obstacles. Cold Regions Science and Technology 49, no. 1: 54–63. doi:10.1016/j.coldregions.2007.01.007.

 Web of Science ®Google Scholar

Oda, K., S. Moriguchi, I. Kamiishi, A. Yashima, K. Sawada, and A. Sato. 2011. Simulation of a snow avalanche model test using computational fluid dynamics. Annals of Glaciology 52, no. 58: 57–64. doi:10.3189/172756411797252284.

 Web of Science ®Google Scholar

Aggarwal, R. K., and A. Kumar. 2012. 2-D computational fluid dynamics model for avalanche flow interaction with an obstacle for snow chute at Dhundhi. International Symposium on Cryosphere and Climate Change (ISCCC): 2-4 April, Manali, India.

 Google Scholar

Salway, A. A. 1978. A seismic and pressure transducer system for monitoring velocities and impact pressures of snow avalanches. Arctic and Alpine Research 10, no. 4: 769–74. doi:10.1080/00040851.1978.12004014.

 Web of Science ®Google Scholar

McClung, D. M., and P. A. Schaerer. 1985. Characteristics of flowing snow and avalanche impact pressures. Annals of Glaciology 6: 9–14. doi:10.3189/1985AoG6-1-9-14.

 Web of Science ®Google Scholar

Sovilla, B., M. Schaer, M. Kern, and P. Bartelt. 2008. Impact pressures and flow regimes in dense snow avalanches observed at the Vall’ee de la Sionne Test Site. Journal of Geophysical Research 113, no. F1: 1–14. doi:10.1029/2006JF000688.

 Web of Science ®Google Scholar

Sovilla, B., M. Schaer, and L. Rammer. 2008. Measurements and analysis of full-scale avalanche impact pressure at the Vallée de la Sionne test site. Cold Regions Science and Technology 51, no. 2–3: 122–37. doi:10.1016/j.coldregions.2007.05.006.

 Web of Science ®Google Scholar

Christen, M., J. Kowalski, and P. Bartelt. 2010. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Regions Science and Technology 63, no. 1–2: 1–14. doi:10.1016/j.coldregions.2010.04.005.

 Web of Science ®Google Scholar

Faug, T., B. Chanut, R. Beguin, M. Naaim, E. Thibert, and D. Baroudi. 2010. A simple analytical model for pressure on obstacles induced by snow avalanches. Annals of Glaciology 51, no. 54: 1–8. doi:10.3189/172756410791386481.

 Web of Science ®Google Scholar

Baroudi, D., B. Sovilla, and E. Thibert. 2011. Effects of flow regime and sensor geometry on snow avalanche impact-pressure measurements. Journal of Glaciology 57, no. 202: 277–88. doi:10.3189/002214311796405988.

 Web of Science ®Google Scholar

Sovilla, B., T. Faug, A. Kohler, D. Baroudi, J. Fischer, and E. Thibert. 2016. Gravitational wet avalanche pressure on pylon-like structures. Cold Regions Science and Technology 126: 66–75. doi:10.1016/j.coldregions.2016.03.002.

 Web of Science ®Google Scholar

Maggioni, M., M. Barbero, F. Barpi, M. Borri-Brunetto, V. de Biagi, M. Freppaz, B. Frigo, O. Pallara, and B. Chiaia. 2019. Snow avalanche impact measurements at the Seehore Test Site in Aosta Valley (NW Italian Alps). Geosciences 9, no. 471: 1–20. doi:10.3390/geosciences9110471.

 Google Scholar

Kyburz, M. L., B. Sovilla, J. Gaume, and C. Ancey. 2022. Physics-based estimates of drag coefficients for the impact pressure calculation of dense snow avalanches. Engineering Structures 254, no. 1–17: 113478. doi:10.1016/j.engstruct.2021.113478.

 Google Scholar

Thibert, E., D. Baroudi, A. Limam, and P. Berthet-Rambaud. 2008. Avalanche impact pressure on an instrumented structure. Cold Regions Science and Technology 54, no. 3: 206–15. doi:10.1016/j.coldregions.2008.01.005.

 Web of Science ®Google Scholar

Baroudi, D., and E. Thibert. 2009. An instrumented structure to measure avalanche impact pressure: Error analysis from Monte Carlo simulations. Cold Regions Science and Technology 59, no. 2–3: 242–50. doi:10.1016/j.coldregions.2009.05.010.

 Web of Science ®Google Scholar

Bovet, E., B. Chiaia, V. de Biagi, and B. Frigo. 2011. Pressure of snow avalanches against buildings. Applied Mechanics and Materials 82: 392–7. doi:10.4028/www.scientific.net/AMM.82.392.

 Google Scholar

Thibert, E., T. Faug, H. Bellot, and D. Baroudi. 2013. Avalanche impact pressure on a plate-like obstacle. International Snow Science Workshop, 7-11 October, Grenoble-Chamonix, France.

 Google Scholar

de Biagi, V., B. Chiaia, and B. Frigo. 2015. Impact of snow avalanche on buildings: Forces estimation from structural back-analyses. Engineering Structures 92, no. 1: 15–28. doi:10.1016/j.engstruct.2015.03.004.

 Google Scholar

Frigo, B., P. Bartelt, B. Chiaia, I. Chiambretti, and M. Maggioni. 2020. Reverse dynamical investigation of the catastrophic wood-snow avalanche of 18 January 2017 at Rigopiano, Gran Sasso National Park, Italy. International Journal of Disaster Risk Science 12, no. 1: 40–55. doi: 10.1007/s13753-020-00306-6.

 Web of Science ®Google Scholar

Fierz, C., R. L. Armstrong, Y. Durand, P. Etchevers, E. Greene, D. M. McClung, K. Nishimura, P. K. Satyawali, and S. A. Sokratov. 2009. The international classification for seasonal snow on the ground. In IHP-VII Technical Documents in Hydrology N°83, IACS Contribution N°1. Paris: UNESCO-IHP.

 Google Scholar