A local meshless method for Cauchy problem of elliptic PDEs in annulus domains

Figures & data

Figure 1. Two $3\times 3$ stencils with four auxiliary points in an annual domain. Black circles represent collocation of the unknown solution value (solution centres). Red stars represent collocation of the PDE governing operator (PDE centres and also these nodes are auxiliary points). Green triangles indicate the system centrepoint; the nodes around which the stencil is formed, and at which the global assembly is performed. Blue squares show boundary points. A centrepoint which located on the red-dashed circle is that for this we consider two stencils.

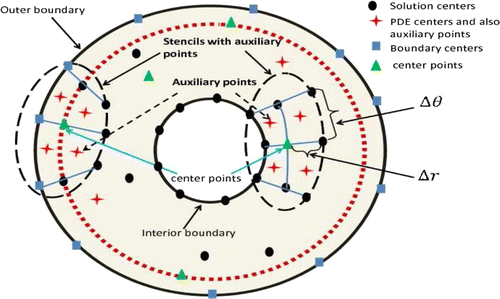
Figure 2. RMS error (left) and condition number (right) versus the shape parameter for the first test problem with no noise.

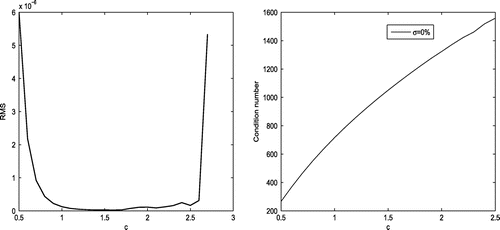
Table 1. Results for numerical approximation of the solution and its normal derivative with different noise levels for the first test problem.

	$u$		${\mathit{\partial }}_{r}u$
$\mathit{\sigma }$	${||e||}_{\infty }$	RMS	${||e||}_{\infty }$	RMS
0	3.8000 $\times {10}^{-6}$	5.3105 $\times {10}^{-7}$	4.4352 $\times {10}^{-5}$	6.8450 $\times {10}^{-6}$
0.01	9.6 $\times {10}^{-3}$	4.9 $\times {10}^{-3}$	2.46 $\times {10}^{-2}$	8.3 $\times {10}^{-3}$
0.05	4.880 $\times {10}^{-2}$	2.99 $\times {10}^{-2}$	2.624 $\times {10}^{-1}$	5.28 $\times {10}^{-2}$
0.1	4.62 $\times {10}^{-2}$	3.45 $\times {10}^{-2}$	2.345 $\times {10}^{-1}$	5.32 $\times {10}^{-2}$

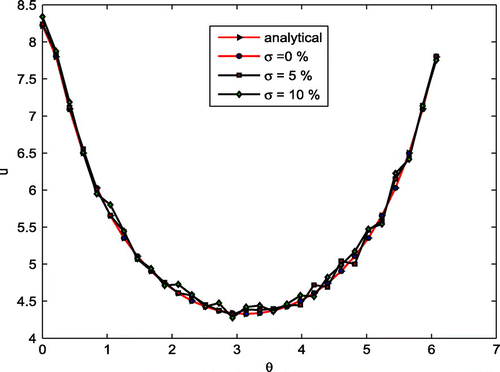
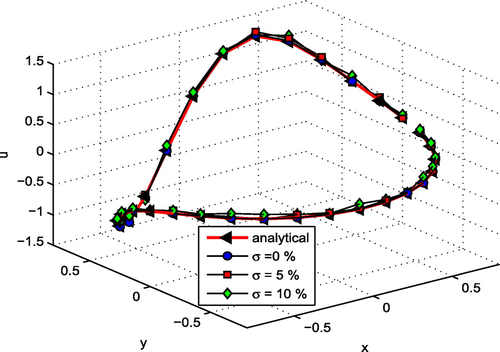
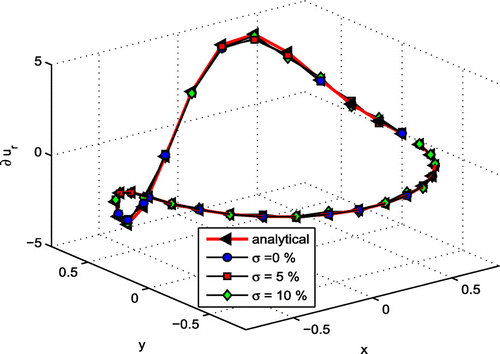
Figure 3. Numerical approximation of the solutions and derivatives with different noise levels over the interior boundary for Poisson equation. (a) Approximate solution with 0% noise, (b) approximate solution with 1% noise, (c) approximate solution with 5% noise, (d) approximate solution with 10% noise, (e) numerical approximation of derivative with 0% noise, (f) numerical approximation of derivative with 1% noise, (g) numerical approximation of derivative with 5% noise and (h) numerical approximation of derivative with 10% noise.

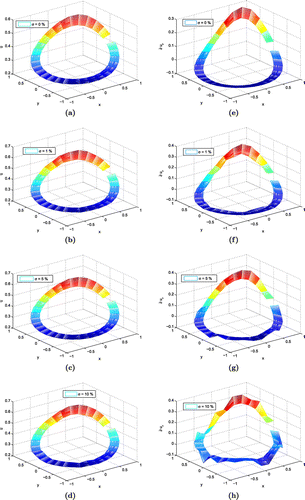
Figure 4. Comparison of the RMS error versus $\mathrm{\Delta }r$ between the proposed method and local RBF method using the first test problem. (a) Approximate solution with 0% noise, (b) approximate solution with 5% noise. FC stands for FC-based method without using auxiliary points, ‘FC+auxil’ stands for FC-based method using auxiliary points and LRBF stands for the local RBF method.

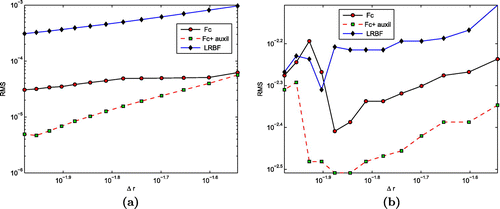
Figure 5. Comparison of the condition number versus $\mathrm{\Delta }r$ using the first test problem. FC stands for FC-based method without using auxiliary points, ‘FC+auxil’ stands for FC-based method using auxiliary points and LRBF stands for the local RBF method.

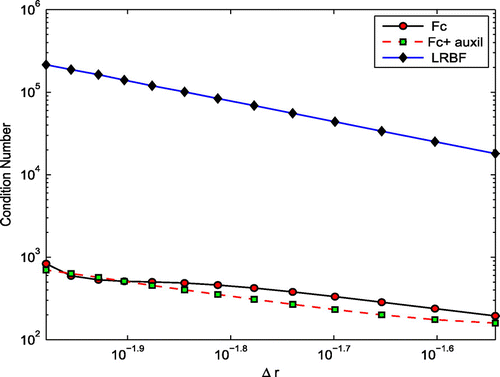
Table 2. Numerical results with different noise levels on two domains for Laplace equation.

	${\mathrm{\Omega }}_1$		${\mathrm{\Omega }}_2$
$\mathit{\sigma }$	${||e||}_{\infty }$	RMS	${||e||}_{\infty }$	RMS
0	1.6 $\times {10}^{-3}$	2.0623 $\times {10}^{-4}$	7.7 $\times {10}^{-3}$	1.1 $\times {10}^{-3}$
0.0001	1.7 $\times {10}^{-3}$	2.2307 $\times {10}^{-4}$	8.0 $\times {10}^{-3}$	1.1 $\times {10}^{-3}$
0.001	2.3 $\times {10}^{-3}$	6.0236 $\times {10}^{-4}$	9.4 $\times {10}^{-3}$	1.4 $\times {10}^{-3}$
0.01	9.9 $\times {10}^{-3}$	4.2 $\times {10}^{-2}$	2.79 $\times {10}^{-2}$	7.4 $\times {10}^{-3}$
0.05	5.12 $\times {10}^{-2}$	2.46 $\times {10}^{-2}$	6.63 $\times {10}^{-2}$	3.22 $\times {10}^{-2}$
0.1	1.215 $\times {10}^{-1}$	4.98 $\times {10}^{-2}$	1.435 $\times {10}^{-1}$	5.61 $\times {10}^{-2}$

Figure 6. Numerical approximation of the solutions and derivatives with different noise levels over the interior boundary for Laplace equation. (a) Approximate solution with 0% noise, (b) approximate solution with 1% noise, (c) approximate solution with 5% noise, (d) approximate solution with 10% noise, (e) numerical approximation of derivative with 0% noise, (f) numerical approximation of derivative with 1% noise, (g) numerical approximation of derivative with 5% noise and (h) numerical approximation of derivative with 10% noise.

Figure 7. Solutions with different noise levels over the interior boundary for Laplace equation.

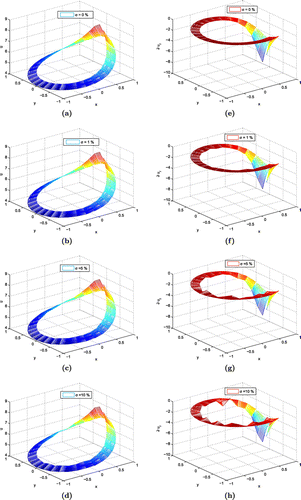
Table 3. RMS error with different noises and different domains for numerical solutions for Helmholtz equation.

$\mathit{\sigma }$	${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\mathrm{\Omega }}_4$	${\mathrm{\Omega }}_5$
0	$2.7408\times {10}^{-6}$	$4.8665\times {10}^{-5}$	$2.8459\times {10}^{-5}$	$6.3925\times {10}^{-6}$
0.01	$1.81\times {10}^{-2}$	$1.13\times {10}^{-2}$	$6.1\times {10}^{-3}$	$4.0\times {10}^{-3}$
0.05	$7.54\times {10}^{-2}$	$5.53\times {10}^{-2}$	$2.53\times {10}^{-2}$	$2.15\times {10}^{-2}$
0.1	$1.632\times {10}^{-1}$	$9.3\times {10}^{-2}$	$4.11\times {10}^{-2}$	$4.22\times {10}^{-2}$

Figure 8. Numerical approximation of solutions and derivatives with different noise levels for Helmholtz equation on domain ${\mathrm{\Omega }}_5$. (a) Approximate solution with 0% noise, (b) approximate solution with 1% noise, (c) approximate solution with 5% noise, (d) approximate solution with 10% noise, (e) numerical approximation of derivative with $0\%$ noise, (f) numerical approximation of derivative with 1% noise, (g) numerical approximation of derivative with 5% noise and (h) numerical approximation of derivative with 10% noise.

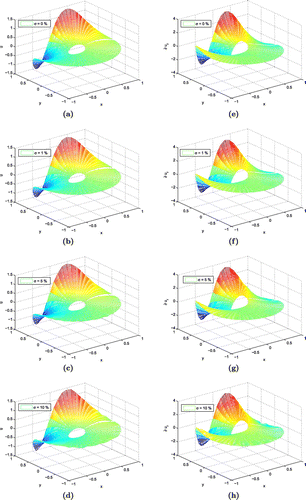
Table 4. Results for numerical approximation of the solutions and normal derivatives with different noise levels for modified Helmholtz equation.

	$u$		${\mathit{\partial }}_{r}u$
$\mathit{\sigma }$	${||e||}_{\infty }$	RMS	${||e||}_{\infty }$	RMS
0	1.7083 $\times {10}^{-5}$	2.9035 $\times {10}^{-6}$	2.5009 $\times {10}^{-4}$	4.1917 $\times {10}^{-5}$
0.01	2.360 $\times {10}^{-2}$	6.301 $\times {10}^{-3}$	1.940 $\times {10}^{-1}$	2.460 $\times {10}^{-2}$
0.05	5.15 $\times {10}^{-2}$	2.32 $\times {10}^{-2}$	2.2 $\times {10}^{-1}$	6.10 $\times {10}^{-2}$
0.1	1.071 $\times {10}^{-1}$	4.75 $\times {10}^{-2}$	2.67 $\times {10}^{-1}$	7.75 $\times {10}^{-2}$

Figure 9. Solutions with different noise levels over the interior boundary for modified Helmholtz equation.

Figure 10. Numerical approximation of derivative with different noise levels over the interior boundary for modified Helmholtz equation.