Collocation method based on shifted Chebyshev and radial basis functions with symmetric variable shape parameter for solving the parabolic inverse problem

Figures & data

Table 1. Some well-known functions that generate RBFs.

$\text{Name of radial basis function}$		$\text{Abbreviations}$		$\text{Definition}$
Multiquadric		$\text{MQ}$		$\varphi (r)=\sqrt{c^2+r^2}$
Inverse Multiquadric		$\text{IMQ}$		$\varphi (r)={\displaystyle \frac{1}{\sqrt{c^2+r^2}}}$
Inverse Quadric		$\text{IQ}$		$\varphi (r)={\displaystyle \frac{1}{c^2+r^2}}$
Gaussian		$\text{GA}$		$\varphi (r)=exp(-c^2{r}^2)$
Thin Plate Spline		$\text{TPS}$		$\varphi (r)=r^{2}log(r)$

Figure 1. Plot of SVSP with $N=21$ and $c^{\ast }=1/\sqrt{6}$.

Table 2. Absolute errors between the exact and approximating solution u(x, 1) at $x=0,0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 1.

x	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0	$-$	$-$	$6.04\times {10}^{-14}$	$4.86\times {10}^{-10}$		$5.80\times {10}^{-16}$	$1.99\times {10}^{-21}$
0.1	$1.92\times {10}^{-7}$	$1.33\times {10}^{-15}$	$4.73\times {10}^{-14}$	$5.89\times {10}^{-10}$		$6.11\times {10}^{-17}$	$7.32\times {10}^{-23}$
0.2	$5.78\times {10}^{-8}$	$3.33\times {10}^{-16}$	$2.14\times {10}^{-14}$	$6.43\times {10}^{-10}$		$1.13\times {10}^{-16}$	$3.01\times {10}^{-23}$
0.3	$5.08\times {10}^{-8}$	$2.11\times {10}^{-15}$	$4.37\times {10}^{-14}$	$6.43\times {10}^{-10}$		$4.55\times {10}^{-18}$	$1.05\times {10}^{-22}$
0.4	$1.30\times {10}^{-7}$	$1.78\times {10}^{-15}$	$2.88\times {10}^{-14}$	$5.89\times {10}^{-10}$		$1.10\times {10}^{-17}$	$2.22\times {10}^{-23}$
0.5	$1.82\times {10}^{-7}$	$1.11\times {10}^{-16}$	$1.05\times {10}^{-15}$	$4.86\times {10}^{-10}$		$6.37\times {10}^{-19}$	$4.19\times {10}^{-23}$
0.6	$2.09\times {10}^{-7}$	$8.88\times {10}^{-16}$	$9.87\times {10}^{-15}$	$3.45\times {10}^{-10}$		$3.15\times {10}^{-18}$	$4.96\times {10}^{-23}$
0.7	$2.18\times {10}^{-7}$	$1.05\times {10}^{-15}$	$4.38\times {10}^{-14}$	$1.78\times {10}^{-10}$		$2.35\times {10}^{-18}$	$4.56\times {10}^{-23}$
0.8	$2.17\times {10}^{-7}$	$1.25\times {10}^{-16}$	$9.06\times {10}^{-14}$	$3.84\times {10}^{-12}$		$1.16\times {10}^{-16}$	$2.35\times {10}^{-23}$
0.9	$2.15\times {10}^{-7}$	$3.61\times {10}^{-16}$	$8.35\times {10}^{-14}$	$1.63\times {10}^{-10}$		$7.46\times {10}^{-17}$	$1.12\times {10}^{-22}$
1	$-$	$-$	$2.60\times {10}^{-14}$	$3.04\times {10}^{-10}$		$6.63\times {10}^{-16}$	$2.08\times {10}^{-21}$

Table 3. Absolute errors between the exact and approximating solution p(t) at $t=0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 1.

t	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0.1	$6.37\times {10}^{-5}$	$4.17\times {10}^{-6}$	$1.20\times {10}^{-11}$	$1.13\times {10}^{-10}$		$1.20\times {10}^{-11}$	$3.18\times {10}^{-15}$
0.2	$5.70\times {10}^{-5}$	$4.17\times {10}^{-6}$	$5.40\times {10}^{-12}$	$1.86\times {10}^{-12}$		$5.42\times {10}^{-12}$	$1.52\times {10}^{-15}$
0.3	$3.37\times {10}^{-4}$	$4.17\times {10}^{-6}$	$6.68\times {10}^{-12}$	$6.04\times {10}^{-14}$		$6.69\times {10}^{-12}$	$6.43\times {10}^{-15}$
0.4	$1.65\times {10}^{-4}$	$4.17\times {10}^{-6}$	$3.23\times {10}^{-11}$	$5.01\times {10}^{-14}$		$3.23\times {10}^{-11}$	$5.99\times {10}^{-15}$
0.5	$4.06\times {10}^{-4}$	$4.17\times {10}^{-6}$	$8.70\times {10}^{-11}$	$2.69\times {10}^{-15}$		$8.70\times {10}^{-11}$	$1.31\times {10}^{-23}$
0.6	$3.94\times {10}^{-5}$	$4.17\times {10}^{-6}$	$1.90\times {10}^{-10}$	$4.41\times {10}^{-14}$		$1.90\times {10}^{-10}$	$1.56\times {10}^{-14}$
0.7	$4.63\times {10}^{-4}$	$4.17\times {10}^{-6}$	$4.02\times {10}^{-10}$	$1.06\times {10}^{-12}$		$4.02\times {10}^{-10}$	$4.53\times {10}^{-14}$
0.8	$4.78\times {10}^{-4}$	$4.17\times {10}^{-6}$	$1.09\times {10}^{-9}$	$1.58\times {10}^{-11}$		$1.09\times {10}^{-9}$	$3.23\times {10}^{-14}$
0.9	$2.18\times {10}^{-3}$	$4.17\times {10}^{-6}$	$3.79\times {10}^{-9}$	$1.04\times {10}^{-9}$		$3.79\times {10}^{-9}$	$2.72\times {10}^{-13}$
1	$2.25\times {10}^{-4}$	$4.17\times {10}^{-6}$	$2.21\times {10}^{-7}$	$3.63\times {10}^{-8}$		$2.21\times {10}^{-7}$	$2.54\times {10}^{-11}$

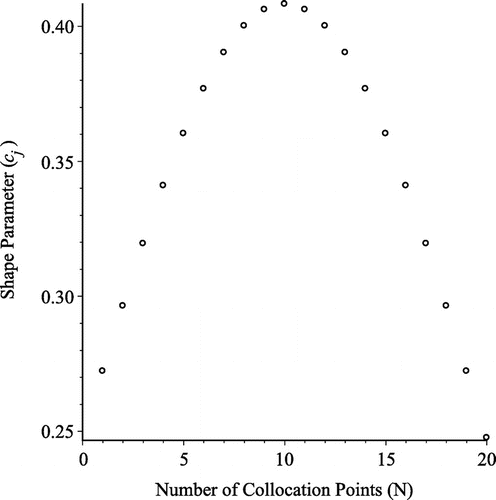
Figure 2. Absolute Error in approximating u(x, 1) (Graph a) and p(t) (Graph b) with $M=21$ and $N=19$ with SVSP for Example 1.

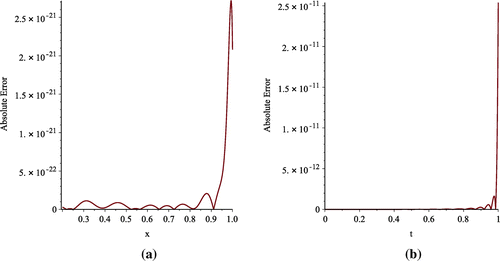
Table 4. The $E_{\infty }$, $E_2$ and RMS errors for u and p for Example 1 with $c=1/\sqrt{6}$ and $c^{\ast }=1/\sqrt{6}$.

		$\text{Present method with CSP}$			$\text{Present method with SVSP}$
$\text{Error}$		$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
$E_{\infty }^u$		$1.19\times {10}^{-13}$	$8.05\times {10}^{-10}$		$9.76\times {10}^{-16}$	$1.94\times {10}^{-21}$
$E_{\infty }^p$		$1.71\times {10}^{-7}$	$3.43\times {10}^{-8}$		$1.71\times {10}^{-7}$	$1.98\times {10}^{-11}$
$E_2^u$		$1.48\times {10}^{-6}$	$1.35\times {10}^{-4}$		$6.45\times {10}^{-8}$	$9.98\times {10}^{-11}$
$E_2^p$		$4.13\times {10}^{-4}$	$2.71\times {10}^{-4}$		$4.13\times {10}^{-4}$	$4.45\times {10}^{-6}$
RMS(u)		$9.62\times {10}^{-8}$	$6.74\times {10}^{-6}$		$4.18\times {10}^{-9}$	$4.99\times {10}^{-12}$
RMS(p)		$1.11\times {10}^{-4}$	$6.22\times {10}^{-5}$		$1.10\times {10}^{-4}$	$1.02\times {10}^{-6}$
$\text{Cond}$		$1.34\times {10}^{14}$	$6.75\times {10}^{14}$		$2.80\times {10}^{13}$	$1.28\times {10}^{14}$

Figure 3. Plot of error function $u-\tilde{u}$ with $M=21$ and $N=19$ using CSP with $c=1/\sqrt{6}$ (Graph a) and SVSP with $c^{\ast }=1/\sqrt{6}$ (Graph b) for Example 1.

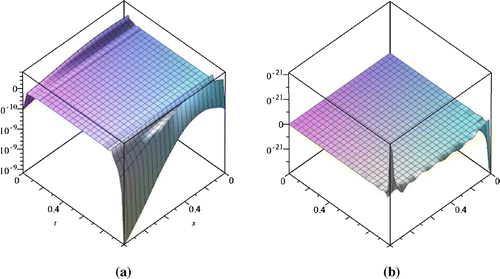
Table 5. Error for approximate u(x, t) with noisy input data for Example 1.

		$E_{\infty }^u\text{with CSP}$				$E_{\infty }^u\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$4.91\times {10}^{-3}$	$2.85\times {10}^{-3}$	$2.01\times {10}^{-3}$		$3.91\times {10}^{-3}$	$3.90\times {10}^{-4}$	$3.90\times {10}^{-5}$
20		$3.63\times {10}^{-2}$	$2.27\times {10}^{-3}$	$2.20\times {10}^{-4}$		$7.43\times {10}^{-3}$	$7.34\times {10}^{-4}$	$7.34\times {10}^{-5}$
30		$6.44\times {10}^{-2}$	$2.62\times {10}^{-2}$	$2.42\times {10}^{-4}$		$1.17\times {10}^{-2}$	$1.18\times {10}^{-3}$	$1.18\times {10}^{-4}$

Table 6. Error for approximate p(t) with noisy input data for Example 1.

		$E_{\infty }^p\text{with CSP}$				$E_{\infty }^p\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$1.50\times {10}^{-1}$	$9.03\times {10}^{-2}$	$7.39\times {10}^{-2}$		$1.86\times {10}^{-1}$	$1.86\times {10}^{-2}$	$1.86\times {10}^{-3}$
20		1.93	$9.87\times {10}^{-1}$	$4.32\times {10}^{-3}$		$2.53\times {10}^{-1}$	$2.56\times {10}^{-2}$	$2.56\times {10}^{-3}$
30		$1.24\times {10}^{-1}$	$1.30\times {10}^{-1}$	$1.45\times {10}^{-2}$		$1.98\times {10}^{-1}$	$1.97\times {10}^{-2}$	$1.96\times {10}^{-3}$

Table 7. Error norms and rate of convergence for various numbers of collocation points with $\eta =40$ for Example 1.

	Rate of convergence with CSP					Rate of convergence with SVSP
M, N	$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$		$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$
2, 2	3.31	$-$	1.95	$-$		1.90	$-$	2.31	$-$
4, 4	0.85	0.98	1.19	0.36		0.56	0.88	1.01	0.60
8, 8	$8.33\times {10}^{-4}$	5.00	$4.60\times {10}^{-2}$	2.35		$1.77\times {10}^{-4}$	5.80	$2.53\times {10}^{-2}$	2.66
16, 16	$9.52\times {10}^{-15}$	18.17	$5.62\times {10}^{-7}$	8.16		$1.39\times {10}^{-14}$	16.80	$2.11\times {10}^{-7}$	8.44
21, 19	$1.40\times {10}^{-9}$	$-26.81$	$2.44\times {10}^{-4}$	$-13.69$		$1.94\times {10}^{-21}$	35.57	$9.98\times {10}^{-11}$	17.25

Table 8. Absolute errors between the exact and approximating solution u(x, 1) at $x=0,0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 2.

x	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0	$-$	$-$	$2.00\times {10}^{-12}$	$2.00\times {10}^{-7}$		$5.08\times {10}^{-14}$	$3.36\times {10}^{-18}$
0.1	$5.76\times {10}^{-9}$	$2.88\times {10}^{-10}$	$4.19\times {10}^{-12}$	$2.97\times {10}^{-7}$		$4.25\times {10}^{-15}$	$3.33\times {10}^{-19}$
0.2	$4.86\times {10}^{-9}$	$4.79\times {10}^{-10}$	$1.11\times {10}^{-12}$	$3.84\times {10}^{-7}$		$6.19\times {10}^{-15}$	$6.64\times {10}^{-20}$
0.3	$3.58\times {10}^{-9}$	$5.01\times {10}^{-10}$	$1.21\times {10}^{-12}$	$4.53\times {10}^{-7}$		$1.07\times {10}^{-16}$	$1.56\times {10}^{-19}$
0.4	$1.91\times {10}^{-9}$	$3.30\times {10}^{-10}$	$6.53\times {10}^{-13}$	$5.09\times {10}^{-7}$		$3.38\times {10}^{-16}$	$3.83\times {10}^{-20}$
0.5	0	0	$1.28\times {10}^{-12}$	$5.44\times {10}^{-7}$		$8.54\times {10}^{-28}$	$5.60\times {10}^{-20}$
0.6	$1.95\times {10}^{-9}$	$4.01\times {10}^{-10}$	$7.49\times {10}^{-14}$	$5.60\times {10}^{-7}$		$5.52\times {10}^{-16}$	$1.12\times {10}^{-19}$
0.7	$3.65\times {10}^{-9}$	$7.44\times {10}^{-10}$	$5.74\times {10}^{-13}$	$5.60\times {10}^{-7}$		$6.38\times {10}^{-17}$	$7.65\times {10}^{-20}$
0.8	$4.84\times {10}^{-9}$	$8.81\times {10}^{-10}$	$1.26\times {10}^{-12}$	$5.41\times {10}^{-7}$		$6.12\times {10}^{-15}$	$3.33\times {10}^{-20}$
0.9	$5.30\times {10}^{-9}$	$6.70\times {10}^{-10}$	$2.43\times {10}^{-13}$	$5.12\times {10}^{-7}$		$3.25\times {10}^{-15}$	$2.29\times {10}^{-19}$
1	$-$	$-$	$6.88\times {10}^{-13}$	$4.69\times {10}^{-7}$		$4.55\times {10}^{-14}$	$2.61\times {10}^{-18}$

Table 9. Absolute errors between the exact and approximating solution p(t) at $t=0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 2.

t	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0.1	$1.60\times {10}^{-3}$	$7.36\times {10}^{-7}$	$6.83\times {10}^{-10}$	$4.35\times {10}^{-5}$		$2.08\times {10}^{-11}$	$3.93\times {10}^{-17}$
0.2	$2.32\times {10}^{-6}$	$7.24\times {10}^{-7}$	$1.09\times {10}^{-10}$	$3.31\times {10}^{-6}$		$2.20\times {10}^{-11}$	$1.34\times {10}^{-17}$
0.3	$8.39\times {10}^{-5}$	$6.65\times {10}^{-7}$	$3.93\times {10}^{-11}$	$7.62\times {10}^{-8}$		$2.29\times {10}^{-11}$	$3.61\times {10}^{-17}$
0.4	$2.35\times {10}^{-4}$	$6.73\times {10}^{-7}$	$2.84\times {10}^{-11}$	$1.31\times {10}^{-10}$		$2.86\times {10}^{-11}$	$2.29\times {10}^{-17}$
0.5	$3.42\times {10}^{-3}$	$6.73\times {10}^{-7}$	$3.60\times {10}^{-11}$	$2.36\times {10}^{-10}$		$3.61\times {10}^{-11}$	$5.99\times {10}^{-19}$
0.6	$2.21\times {10}^{-3}$	$6.63\times {10}^{-7}$	$4.64\times {10}^{-11}$	$9.63\times {10}^{-10}$		$4.37\times {10}^{-11}$	$2.20\times {10}^{-17}$
0.7	$1.08\times {10}^{-3}$	$6.68\times {10}^{-7}$	$5.86\times {10}^{-11}$	$1.10\times {10}^{-7}$		$5.54\times {10}^{-11}$	$3.71\times {10}^{-17}$
0.8	$3.07\times {10}^{-4}$	$6.89\times {10}^{-7}$	$1.94\times {10}^{-10}$	$3.57\times {10}^{-6}$		$9.34\times {10}^{-11}$	$2.50\times {10}^{-17}$
0.9	$5.63\times {10}^{-4}$	$7.26\times {10}^{-7}$	$4.64\times {10}^{-10}$	$4.40\times {10}^{-5}$		$2.05\times {10}^{-10}$	$3.78\times {10}^{-17}$
1	$-$	$-$	$6.76\times {10}^{-9}$	$1.85\times {10}^{-4}$		$7.62\times {10}^{-9}$	$8.90\times {10}^{-17}$

Figure 4. Absolute Error in approximating u(x, 1) (Graph a) and p(t) (Graph b) with $M=21$ and $N=19$ with SVSP for Example 2.

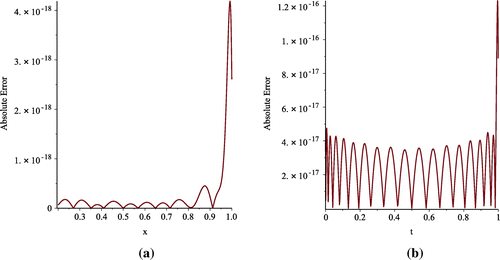
Table 10. The $E_{\infty }$, $E_2$ and RMS errors for u and p for Example 2 with $c=1/\sqrt{6}$ and $c^{\ast }=1/\sqrt{6}$.

		$\text{Present method with CSP}$			$\text{Present method with SVSP}$
$\text{Error}$		$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
$E_{\infty }^u$		$2.71\times {10}^{-11}$	$1.47\times {10}^{-6}$		$5.92\times {10}^{-14}$	$4.12\times {10}^{-18}$
$E_{\infty }^p$		$4.81\times {10}^{-9}$	$1.84\times {10}^{-4}$		$5.97\times {10}^{-9}$	$1.13\times {10}^{-16}$
$E_2^u$		$3.65\times {10}^{-5}$	$9.67\times {10}^{-3}$		$6.61\times {10}^{-7}$	$5.32\times {10}^{-9}$
$E_2^p$		$1.16\times {10}^{-4}$	$3.36\times {10}^{-2}$		$7.73\times {10}^{-5}$	$1.23\times {10}^{-8}$
RMS(u)		$2.37\times {10}^{-6}$	$4.84\times {10}^{-4}$		$4.28\times {10}^{-8}$	$2.66\times {10}^{-10}$
RMS(p)		$3.09\times {10}^{-5}$	$7.71\times {10}^{-3}$		$2.07\times {10}^{-5}$	$2.82\times {10}^{-9}$
$\text{Cond}$		$2.47\times {10}^{13}$	$1.70\times {10}^{15}$		$1.96\times {10}^{13}$	$5.23\times {10}^{14}$

Figure 5. Plot of error function $u-\tilde{u}$ with $M=21$ and $N=19$ using CSP with $c=1/\sqrt{6}$ (Graph a) and VSP with $c^{\ast }=1/\sqrt{6}$ (Graph b) for Example 2.

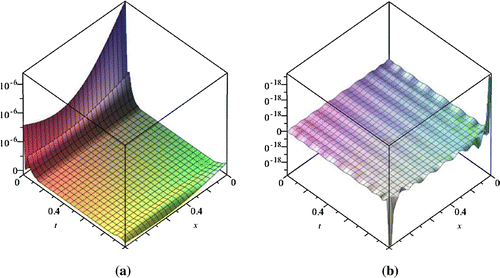
Table 11. Error for approximate u(x, t) with noisy input data for Example 2.

		$E_{\infty }^u\text{with CSP}$				$E_{\infty }^u\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$1.03\times {10}^{-2}$	$1.10\times {10}^{-3}$	$2.02\times {10}^{-3}$		$9.80\times {10}^{-4}$	$9.80\times {10}^{-5}$	$9.80\times {10}^{-6}$
20		$1.22\times {10}^{-2}$	$1.56\times {10}^{-3}$	$1.88\times {10}^{-4}$		$1.01\times {10}^{-3}$	$1.01\times {10}^{-4}$	$1.01\times {10}^{-5}$
30		$7.12\times {10}^{-3}$	$3.26\times {10}^{-3}$	$1.48\times {10}^{-3}$		$1.84\times {10}^{-3}$	$1.73\times {10}^{-4}$	$1.72\times {10}^{-5}$

Table 12. Error for approximate p(t) with noisy input data for Example 2.

		$E_{\infty }^p\text{with CSP}$				$E_{\infty }^p\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$8.94\times {10}^{-1}$	$1.83\times {10}^{-1}$	$2.04\times {10}^{-1}$		$5.36\times {10}^{-1}$	$5.46\times {10}^{-2}$	$5.46\times {10}^{-3}$
20		2.22	$3.69\times {10}^{-1}$	$3.83\times {10}^{-2}$		$8.20\times {10}^{-1}$	$8.08\times {10}^{-2}$	$8.08\times {10}^{-3}$
30		1.67	$1.64\times {10}^{-1}$	$1.94\times {10}^{-1}$		$9.61\times {10}^{-1}$	$9.75\times {10}^{-2}$	$9.76\times {10}^{-3}$

Table 13. Error norms and rate of convergence for various numbers of collocation points with $\eta =40$ for Example 2.

	Rate of convergence with CSP					Rate of convergence with SVSP
M, N	$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$		$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$
2, 2	0.44	$-$	0.88	$-$		0.28	$-$	0.72	$-$
4, 4	$6.81\times {10}^{-3}$	3.01	0.17	1.19		$7.08\times {10}^{-3}$	2.65	0.17	1.04
8, 8	$9.33\times {10}^{-6}$	4.76	$6.97\times {10}^{-3}$	2.30		$6.19\times {10}^{-6}$	5.08	$5.48\times {10}^{-3}$	2.48
16, 16	$1.04\times {10}^{-12}$	11.55	$5.17\times {10}^{-6}$	5.20		$4.66\times {10}^{-13}$	11.83	$1.92\times {10}^{-6}$	5.74
21, 19	$1.99\times {10}^{-6}$	$-32.59$	$7.92\times {10}^{-3}$	$-16.53$		$4.12\times {10}^{-18}$	26.22	$5.32\times {10}^{-9}$	13.27

Dehghan M , Shakeri F . Method of lines solutions of the parabolic inverse problem with an overspecification at a point. Numer Algorithm. 2009;50:417–437.

 Web of Science ®Google Scholar

Mohebbi A , Abbasi M . A fourth-order compact difference scheme for the parabolic inverse problem with an overspecification at a point. Inverse Prob Sci Eng. 2015;23(3):457–478.

 Web of Science ®Google Scholar