Figures & data
Figure 1. The Tonnetz.
Figure 2. L, P, and R triangle flips for minor triads (left) and major triads (right). Each flip fixes an edge whose vertices represent common tones; the third voice moves by one or two semitones.
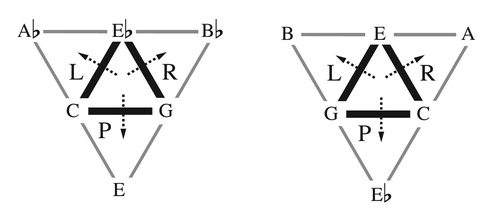
Figure 3. The solid path represents the LP cycle (LPLPLP) and returns each note to its starting point; the dashed path represents the PR cycle (PRPRPRPR) and moves each voice downward along the C major chord.
Figure 4. Two paths on the chart of the regions, again with different effects.
Figure 5. Lerdahl’s toroidal model of diatonic triads, along with two paths in the space.
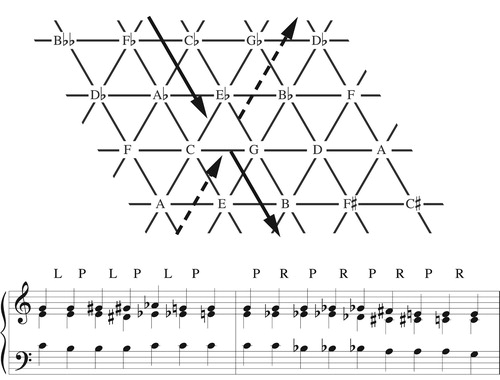
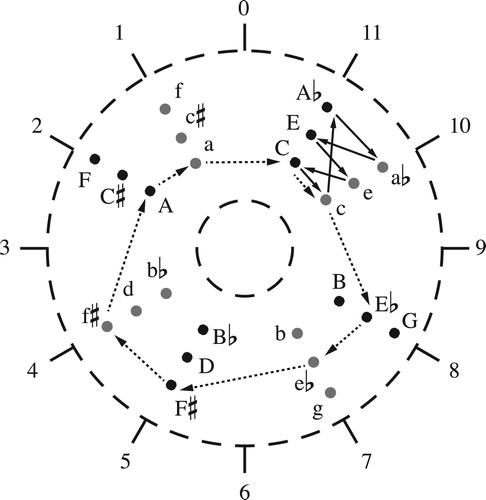
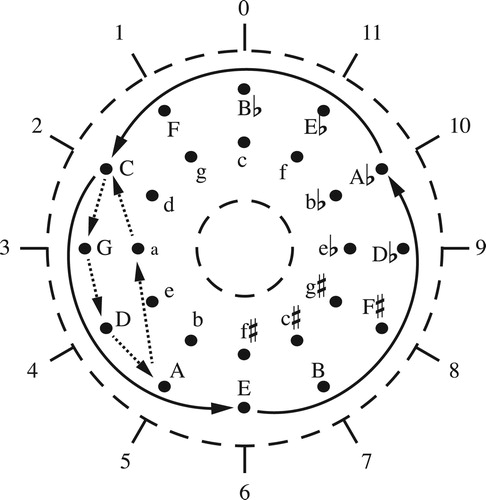
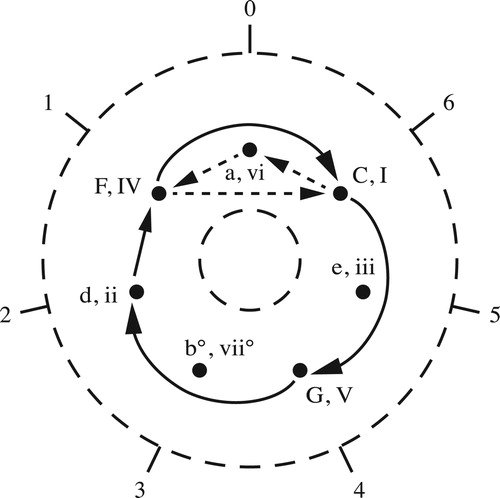
Figure 6. Annular models of chromatic and diatonic space. Angular position corresponds to pitch-class sum.
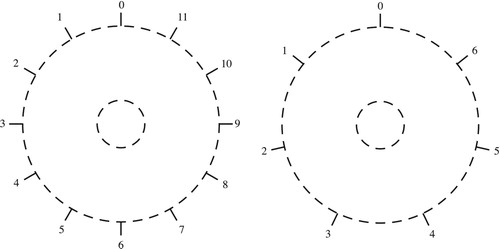
Figure 7. Trajectories in the annular spaces are determined by the sum of the real numbers in a voice leading’s pitch-class paths.
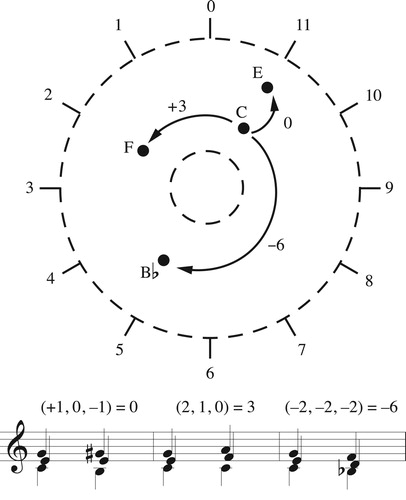
Figure 8. Loops such as A and B, which do not enclose the center of the space, return each voice to its starting point, as in the passages in (b). Loops such as C, which do enclose the center of the space, represent “transpositions along the chord” in which each note moves up or down by one chordal step (c). The top staff of (c) shows the voice leadings while the bottom staff shows that they each involve an octave of total motion in all voices.
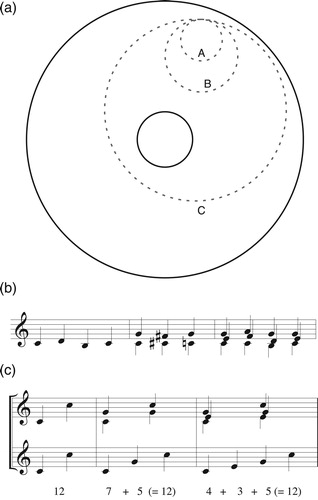
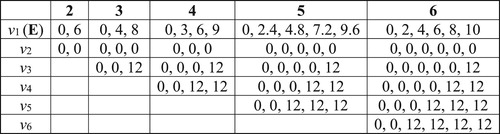
Figure 9. The voice leadings between two separate chords X and Y can be written as a fixed voice leading X→Y composed with some number of loops Y→Y. In the annular space, the numbers represent sum of the real components in voice leadings X (which takes fø7 to E7) and ti (which are the transpositions up and down i steps along the chord E–G♯–B–D).
Figure 10. The paths in in annular space.
Figure 11. The paths in in annular space. Here I represent minor keys with harmonic-minor scales.
Figure 12. The paths in in annular space.
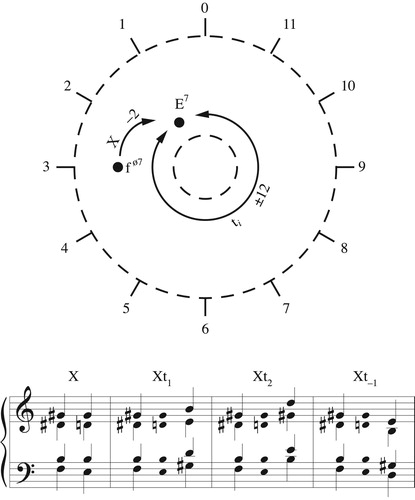
Figure 13. Three diatonic voice leadings that can be represented by the same graph. Lowercase t represents transposition along the chord; uppercase T represents transposition along the diatonic scale.
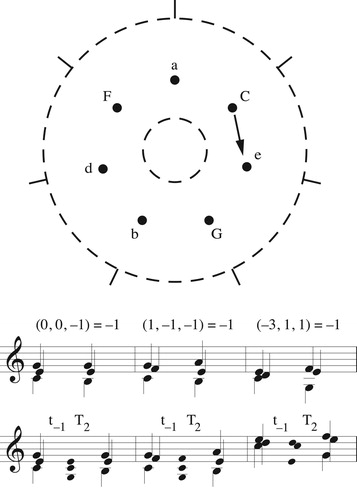
Figure 14. Three chromatic voice leadings that can be represented by the same graph. Lowercase t represents transposition along the chord while boldface T represents transposition along the chromatic scale.
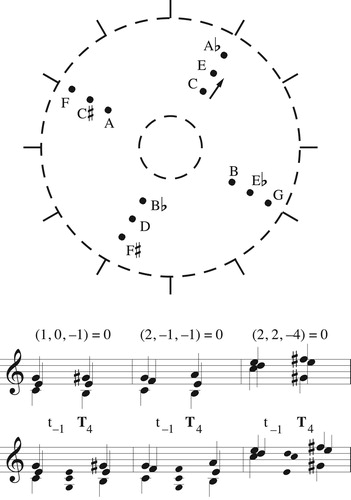
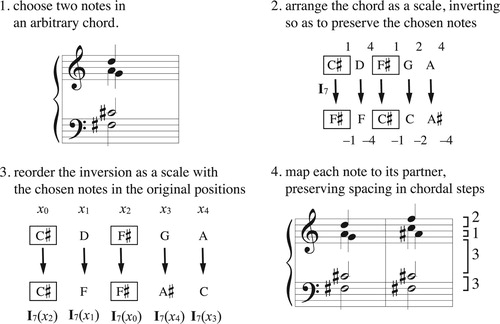
Figure 15. Two strategies of registral inversion. (a) Placing the bottom note of a chord at the top. (b–c) Moving each voice by one chordal step, preserving the chord’s registral spacing when measured in steps along the chord.
Figure 16. Generating a sequence of complex harmonies by combining motion along the chord with motion along the scale. The top system moves by one step along the initial chord. The bottom system transposes these harmonies chromatically to produce a progression of sonorities with the same spacing as measured in chordal steps.
Figure 17. A hierarchical passage in which chords and scales each take short counterclockwise motions in their respective annular spaces. Here, r, t, f, s, and n stand for root, third, fifth, seventh, and ninth.
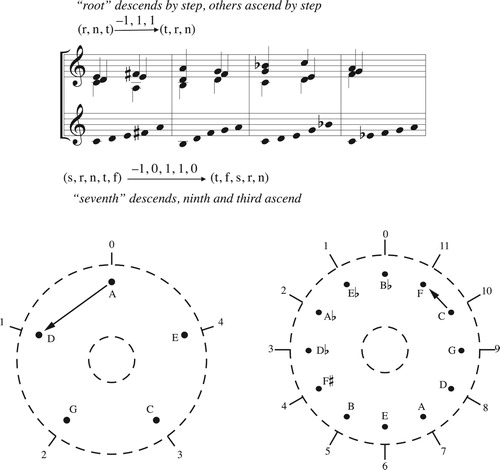
Figure 18. (top) Annular space for the diatonic hexachord. (bottom) Scrambling the voice leadings in any repeating voice-leading pattern produces analogues to the melodic minor collection. Here, the boldfaced chords represent a generalized “circle of fifths” that moves radially in annular space; by rearranging every pair of these voice leadings we obtain alternate pathways, generating hexatonic scales. See CitationTymoczko (2011, §3.11) for more.
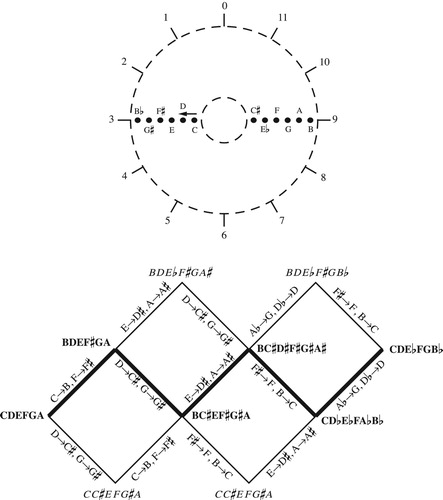
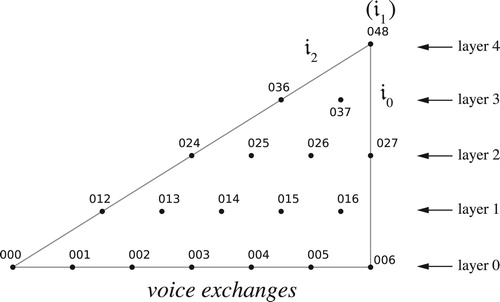
Figure 19. Annular space for dyads in a seven-note scale, with the loops representing two basic voice exchanges. For the diatonic third, these move notes by two and five contrary-motion steps respectively.
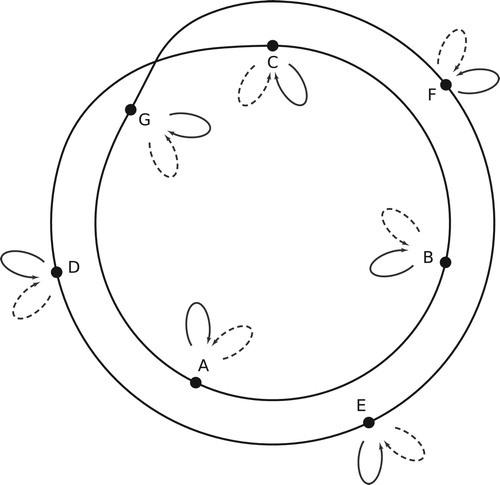
Figure 20. Individually T-related voice leadings, representing the same voice leading in transpositional set-class space. The chords in the top voice leading are transposed by different amounts to produce the bottom voice leading. Nevertheless, both begin with major chords, moving root by c, the third by c + 1, and fifth by c + 2. A single path in set-class space represents all such voice leadings, starting at any major chord and for every value of c.
Figure 21. In trichordal set-class space, three ascending steps-along-the-chord are equal to the identity.
Figure 22. Let (x0, x1, … , xn–1) be a chord in non-descending pitch-class order spanning less than an octave. The combination of transposition along the chord and transposition along the scale moves the pitch class xi to the pitch class xi+c mod n + d, with addition acting on both pitch classes and voice labels. Voices move along paths ||xi+c–xi||+ + d, where ||xi+c–xi||+ is the ascending c-step scalar interval from xi to xi+c, which is xi+c–xi if i + c ≥ i and xi+c–xi + o otherwise. In set-class space we ignore d, while in the annular spaces we do not.
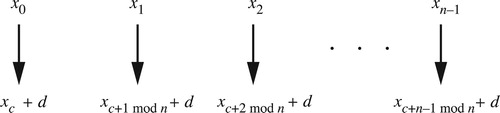
Figure 23. Polygons representing set-class spaces for three, four, five, and six notes. Dark dots represent a chord’s normal form, light dots its inversion; arrows represent sides that are glued together. E is the completely even chord dividing the octave into n pieces.
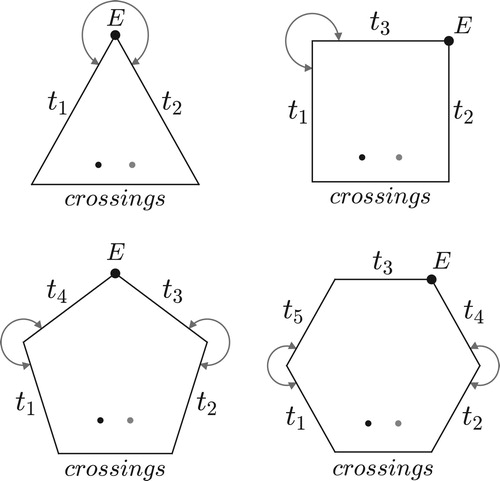
Figure 24. Pentachordal transpositional set-class space, with a path representing one-step transposition-along-the-chord. If we choose the dark point to represent the standard pentatonic scale, then this path will correspond to all of the voice leadings on the top system; if the point represents the dominant ninth chord, then the path corresponds to those on the bottom.
Figure 25. (a) The opening voice leading of Tristan, (b) the path it takes through tetrachordal transpositional set-class space, and (c) its appearance in the polygonal representation.
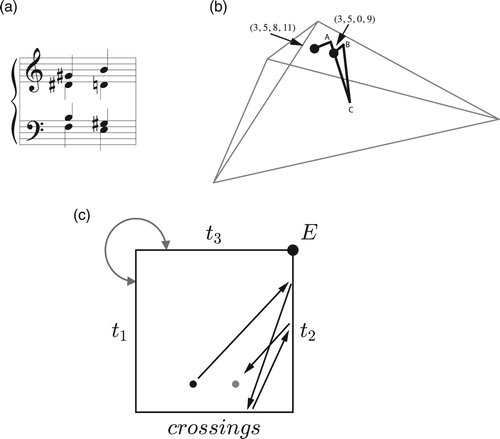
Figure 26. The opening voice leading of Tristan with the second chord transposed up by semitone, and each voice making a smooth glissando from start to finish. The glissando touches the t2 boundary when the moving voices are two semitones apart and the crossing boundary when they sound the same pitch class.
Figure 27. A transformational interpretation of the opening of Tristan, in which the boundary interactions are treated as voice leadings from the Tristan chord to itself. Here r, t, f, s stand for root, third, fifth, and seventh.
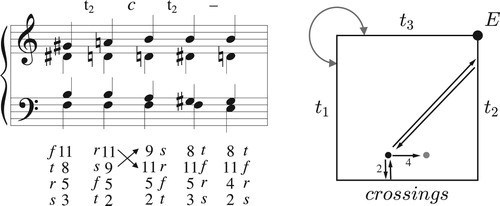
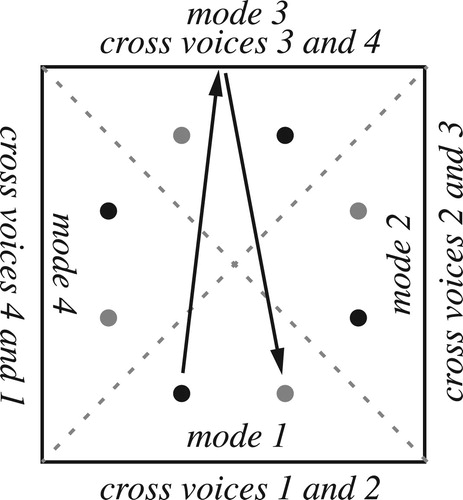
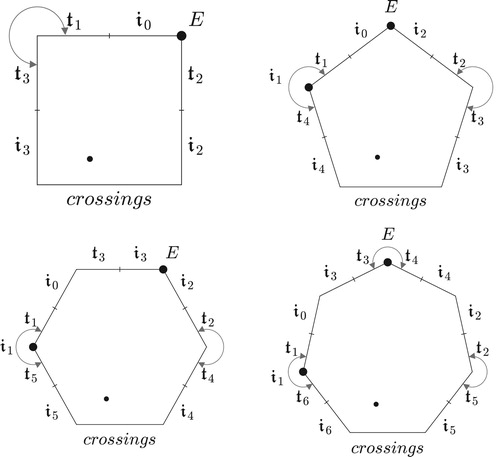
Figure 28. The permutation region represents the cross section of annular space; its n boundaries represent the n exchanges of pairwise voices. Each of its n regions contains a different mode of each set class.
Figure 29. The first voice leading of Tristan plotted in the permutation region.
Figure 30. The vertices of transpositional set-class space for dimensions two through six.
Figure 31. Transpositional set-class space has the structure of a cone.
Figure 32. The semitonal layer of tetrachordal set-class space.
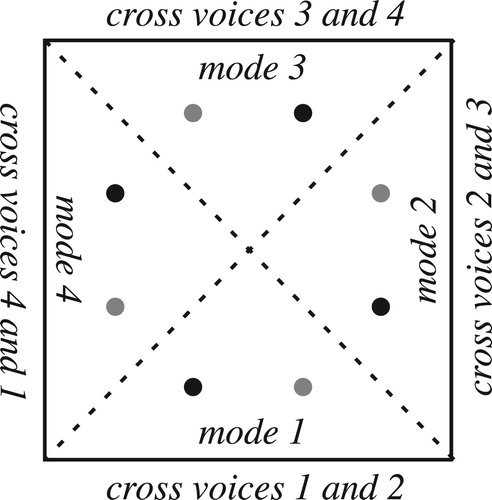
Figure 33. The 1, 3 face of tetrachordal transpositional set-class space. The central line is transpositionally symmetrical; each chord on the right side has a partner on the left.
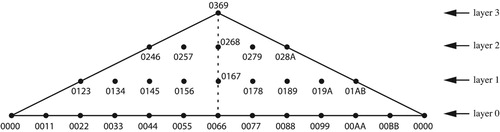
Figure 34. Two paths in trichord space, along with instances of the voice leadings they represent. We need to transpose β by one step upward along the chord to attach it to the endpoint of α.
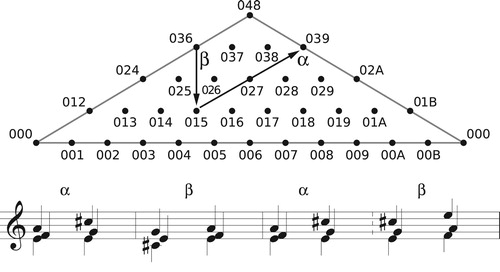
Figure 35. A single diagram in tetrachordal transpositional set-class space that can represent a four-chord progression from Schoenberg, a similar progression using just a single set class, or a descending-fifth series of extended dominants. In the first and third cases we conceive of our musical object as a region of set class space (the dotted oval); in the second, this region shrinks to a point, as in traditional set theory.
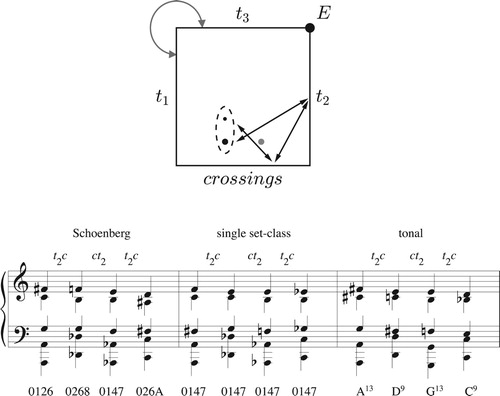
Figure 36. Linear interpolation (0, 1, 4, 6)→(1, 4, 6, 12) produces a generalized line segment that interacts with the t3 and t2 boundaries.
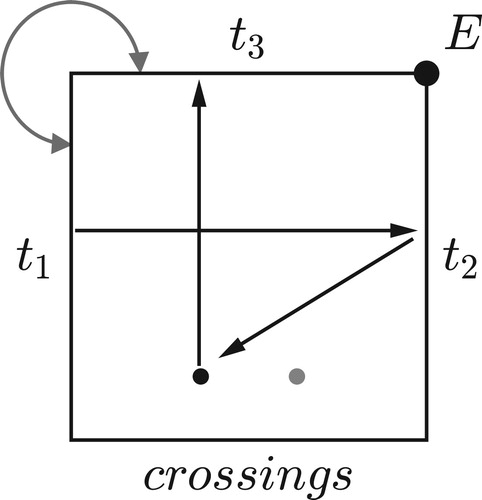
Figure 37. The effect of this path cannot be described topologically as it depends on the intervallic structure of the chord.
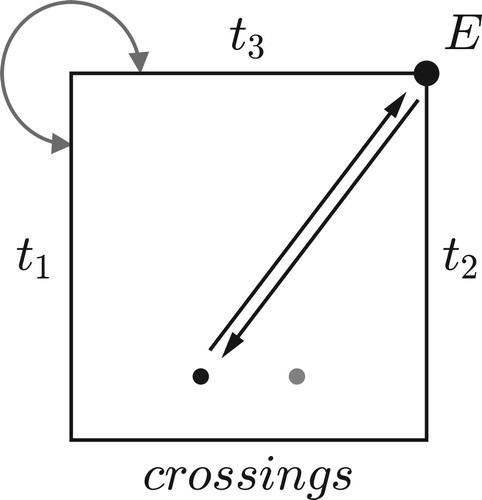
Figure 38. All of these voice leadings are represented by the same path in inversional set-class space. That path represents voice leadings that either start with a major triad, moving root by c and third and fifth by c + 1 semitones, or start with a minor triad, moving root and third by c–1 semitones and fifth by c semitones.
Figure 39. Let (x0, x1, … , xn–1) be a chord in non-descending pitch-class order spanning less than an octave. A strongly crossing-free voice leading from a chord to its inversion moves the pitch class xi to the pitch class d–xc–i mod n, with subtraction acting on both pitch classes and voice labels. Voices move along paths d–xc–xi + ||xc–xc–i mod n||+, with ||x||+ defined as in .
Figure 40. A recipe for constructing a generalized neo-Riemannian transformation.
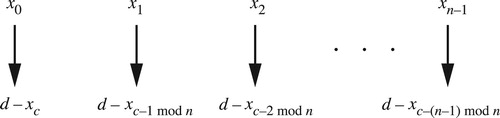
Figure 41. Combining neo-Riemannian voice leadings with chromatic transposition to generate a wealth of related sonorities from a single starting point. The inversional labels 𝔦i will be explained shortly.
Figure 42. The operation applied to a normal-form chord (left), where it moves x0 to x0, and its inversion (right), where it moves x0 to x2. Each voice leading is the other’s inverse. Subscripts are relative to each chord’s transpositional normal form.
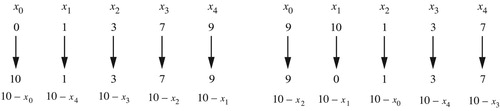
Figure 43. Polygonal models of the neo-Riemannian set-class voice leadings for the major/minor triad (left), the half-diminished/dominant seventh (center), and the 01378 pentachord in (right). Bold labels are on the front of the polygon, italics on the reverse side. The neo-Riemannian set-class voice leadings are flips around different axes; two such flips form a rotation that transposes the two sides in opposite directions along the chord.
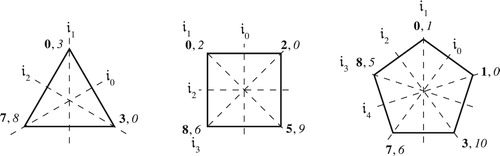
Figure 44. Schematic models of inversional set-class space, for trichords, tetrachords, pentachords, and hexachords. These graphs involve slight simplifications that will be described shortly.
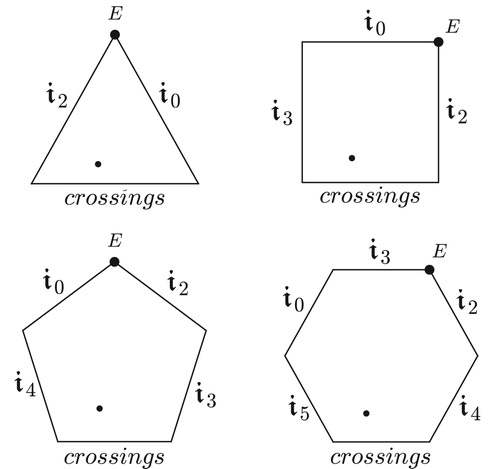
Figure 45. Passages in which two voices descend in parallel while the third alternates between prime and inverted forms: Mozart, C major piano sonata K. 309, I, mm. 73–76, featuring the voice leading; the Benedictus from Schnittke’s Requiem, featuring
; and the opening of Gesualdo’s Moro Lasso, featuring
.
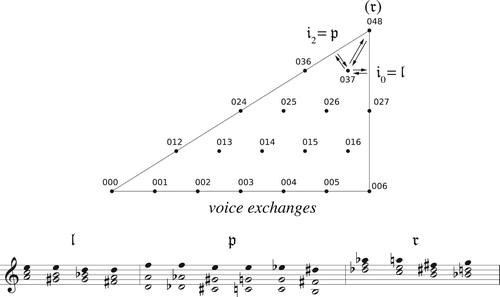
Figure 46. Three passages in The Rite of Spring that connect 016 trichords using generalized neo-Riemannian voice leadings: (top left) R114, m. 2 (solid line); (top right) R15, m. 1 (dotted line); (bottom) R64, mm. 5–6 (brass part only, solid line).
Figure 47. Measures 4–6 present fifteen successive 𝔦2 voice leadings relating 015 and 025 set classes.
Figure 48. A passage from the Rite of Spring involving inversionally related four-note chords; the interval between alto and tenor is always eight semitones; between soprano and bass is fifteen semitones. The entire passage is a repeating series of 𝔦2 voice leadings.
Figure 49. A comparison of the vertices and facets for transpositional and inversional set-class space. Here “opposite facet” means the facet that does not contain the vertex in question.
Figure 50. Trichordal inversional set-class space as a cone.
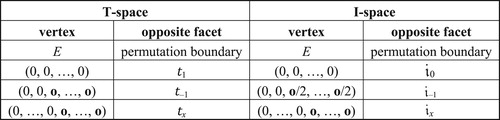
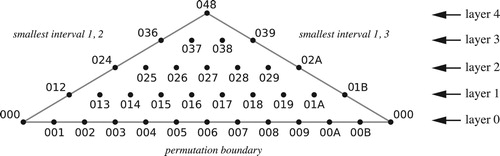
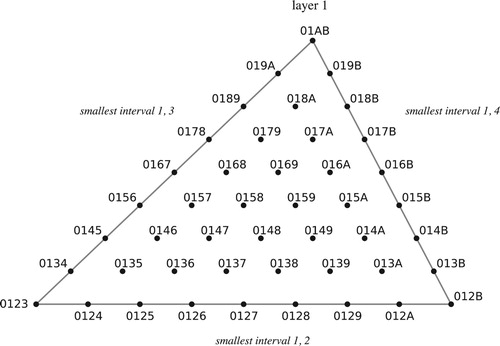
Figure 51. Three layers of tetrachordal inversional set-class space, with smallest interval 0, 1, and 2.
Figure 52. Two layers of pentachordal inversional set-class space, with smallest interval 1 and 2.
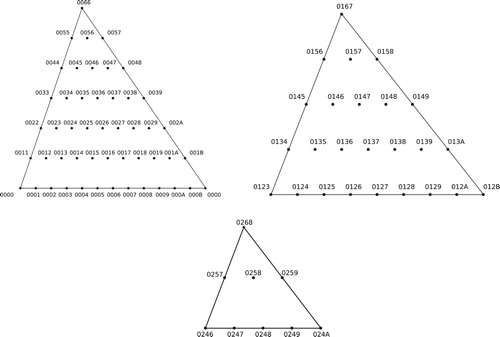
Figure 53. If two normal-form orderings are related by 𝔦–1, then their first and second intervals (a and b) must be the same size, and no larger than any other interval. For 𝔦–2 this is true of the first and third intervals (a and c).
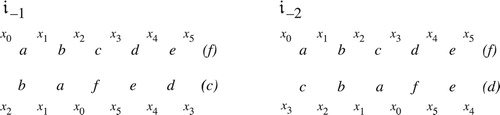
Figure 54. Four-note inversional set-class space contains subspaces representing 𝔱1 and 𝔱2; the former consists of a pair of glued-together line segments, and the latter a mirror-like line segment of 𝔱2-symmetrical chords. There can no subspace representing 𝔦1-invariant set classes, for such chords would have step-interval sequence abcd by hypothesis equal to dcba, which by NF1–4 implies a = b = c = d. The voice leading in the first example, when represented by linear interpolation, passes through the identified line segment; this is the origin of the square root.
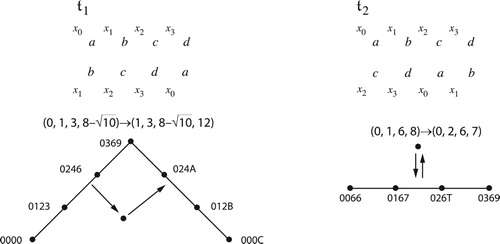
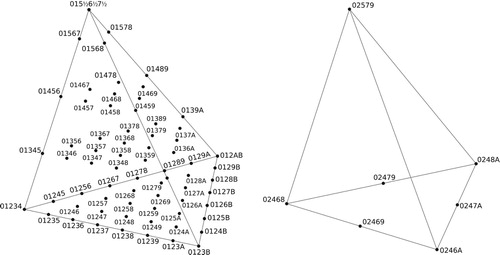
Figure 55. The semitonal layer of the 𝔦2 and 𝔦3 facets of pentachordal space. The shaded triangles are glued together as in transpositional space, representing 𝔱±2. The lighter areas contain pairs of inversionally related chords, with the dotted line inversionally symmetrical. Every chord on the 𝔦3 facet either has an inversional partner on its facet or a transpositional partner on the 𝔦2 facet: if its normal-form step-interval sequence is abcde, then its 𝔱2 and 𝔦3 orderings are cdeab and cbaed respectively; if d ≤ b, the t2 ordering is normal and on the 𝔦2 facet; if b ≤ d, the 𝔦3 ordering is normal and on the 𝔦3 facet. If b = d, then both situations obtain. See the appendix for a more general argument.
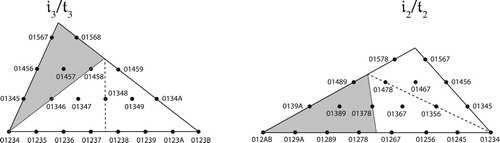
Figure 56. The semitonal layer of the 𝔦4/𝔱4 and 𝔦0/𝔱1 facets of pentachordal inversional set-class space. Each facet is divided into in inversionally related halves. However, their bottom edges are glued together and can represent transposition: thus a 𝔱–1 voice leading can move from the interior of the space to the bottom edge of the 𝔦4 boundary, reappear on the bottom edge of 𝔦0 facet, and return to its starting point, just like the transpositional case.
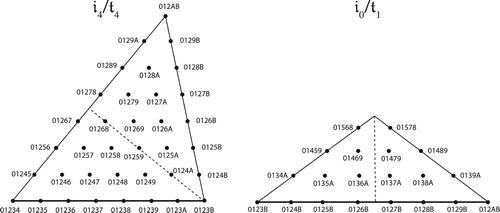
Figure 57. Subspaces invariant under 𝔦1. (a) In pentachordal space, this is a line containing interval cycles. The voice leading on the figure moves from the interior of the space, reflects off the line and returns to itself, acting as 𝔦1. (b) In heptachordal inversional set-class space, there is a two-dimensional subspace of chords symmetrical under i1, containing sets of the form (0, a, 2a, 2a + b, 12 − 2a − b, 12 − 2a, 12 − a), with a ≤ b, and a ≤ 12 − 4a − 2b.
Figure 58. A more accurate picture of inversional set-class space for n = 4, 5, 6, 7.
Figure 59. The dotted line is the path traced out by the two-step ascending transposition-along-the-chord (0, 1, 3, 5, 7)→(3, 5, 7, 12, 13); the solid line represents the two-step ascending transposition-along-the-chord (0, 1, 3, 5, 9)→(3, 5, 9, 12, 13). Here linear interpolation produces different patterns of boundary interactions.
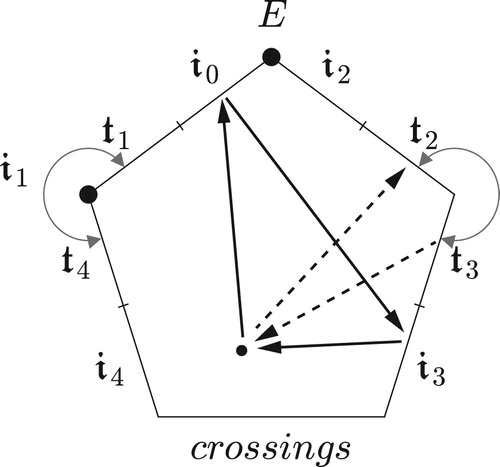
Figure 60. Dualistic and non-dualistic versions of the basic voice-leading transformations. On the left, the transformation expressed with the inversionally normal half-diminished seventh; in the middle, a non-dualistic equivalent; on the right, the dualistic form. The transformations can be expressed by their effect on a normally ordered collection: c3 exchanges the second and third notes of the normal ordering, t1 moves each note up by one step along the normal ordering, and i1 is the crossing-free voice leading between the chord and its inversion that sends the smallest interval down by one order position when the first chord is normally ordered.
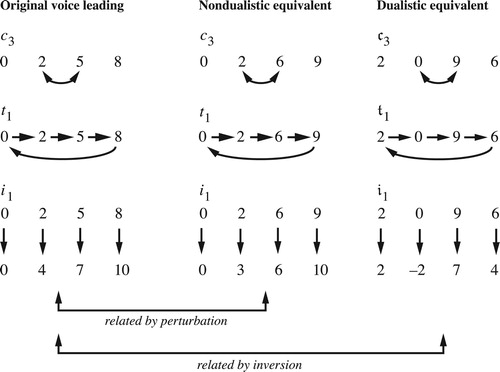
Figure 61. Four voice leadings from the Tristan prelude along with their descriptions in the alphabet.
Figure 62. The twelve elements of the basic tetrachordal alphabet in the permutation region. On the left, the inversionally normal half-diminished seventh. In the middle, the non-dualistic versions of these transformations as applied to the dominant seventh. On the right, the dualistic equivalents, reflecting the left figure along its vertical center.
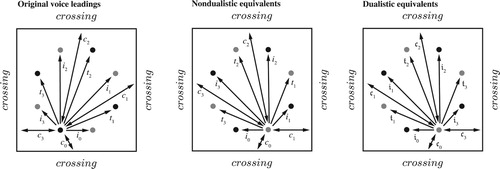
Figure 63. The four Tristan voice leadings plotted in the tetrachordal permutation region. The first three touch a crossing boundary and arrive at the opposite dominant-seventh. The last is the retrograde inversion of such a path.
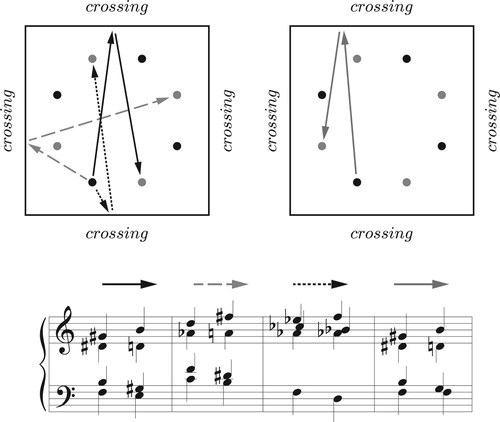
Figure 64. The four Tristan voice leadings in inversional set-class space. The paths are much less comprehensible than in the preceding figure.
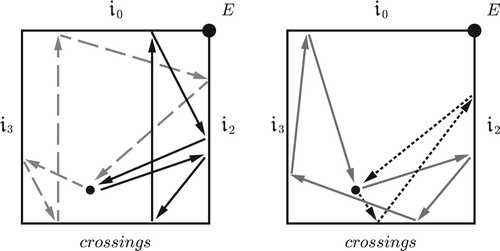
Figure 65. The semitonal layer of the intersection of the t2 and t4 boundaries in hexachordal set-class space, containing set classes that remain in normal form under both t2 and t–2 and whose smallest interval appears in the first, third, and fifth positions of the normal ordering. Each set class appears three times and is mapped onto its equivalents by 120° rotation. The central point, meanwhile, is symmetrical under t2, and hence acts like a mirror in the higher dimensional orbifold. Nearby chords like (0, 0.1, 4, 4.2, 8, 8.3) can be nearly symmetrical under t2 even though they are close to the base of the cone.
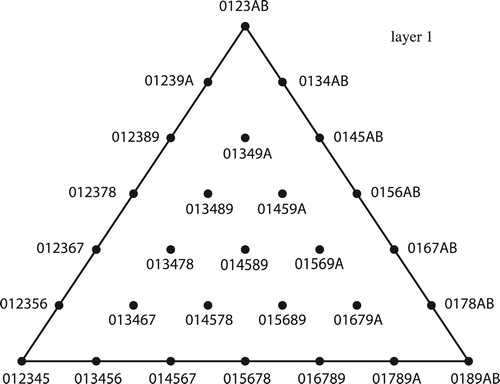
Figure 66. Mark Levine’s illustration of the five inversions of the “So What” chord. Each voice ascends by step along the pentatonic scale D–F–G–A–C.
Figure 67. Rudresh Mahanthappa’s 2006 composition “The Decider” is based on the 025 set class, moving the perfect fourth in parallel, the middle voice alternately a major second below the top voice and a major second above the bottom. This is very similar to Figures and above.
Figure 68. In the annular spaces, traditional transposition and inversion are geometrically straightforward, corresponding to rotation and reflection (here around the solid line). By contrast, dualistic transpositions-along-the-chord move inversions in opposite directions and hence do not correspond to standard geometrical symmetries.
Figure A1. A passage of music containing voice leadings from the singular (A, A) to itself. This passage defines a unique melodic design, but can be described in multiple ways using elements from the orbifold fundamental group.
