Mathematical specification of hitomezashi designs

Figures & data

Figure 1. A mathematically-designed stitch pattern for hitomezashi. This piece has been worked on light Aida cloth using dark cotton thread. The traditional roles of dark cloth and light thread have been exchanged.

Figure 2. Notice how different sequences of vertical stitches on the left and on the right interact with common lines of horizontal stitches to give different patterns. This piece has been worked with cotton thread on hessian (burlap).

Figure 3. Hitomezashi as a stitch form can incorporate crossing stitches and diagonal stitches. This design features both.

Figure 4. Starting to decorate a small square coaster with hitomezashi. The first 10 vertical lines of running stitch have been completed.

Figure 5. The two sides of a coaster decorated with hitomezashi. On the reverse of a pattern of offset crosses jūjizashi, a regular pattern of small squares and stepped lines (kuchi and yamagata) is formed.

Figure 6. Vertical lines of stitching obtained by stitching the pattern specified by the word $v$ = 01 as many times as desired, and to the height desired. This pattern is called tategushi.

Figure 7. (a) Linked steps (dan tsunagi) that rise as we move to the right. (b) The same stitch design in the other possible orientation, drawn and to a different scale. This orientation is encoded by $v$ = 10; $w$ = 10.

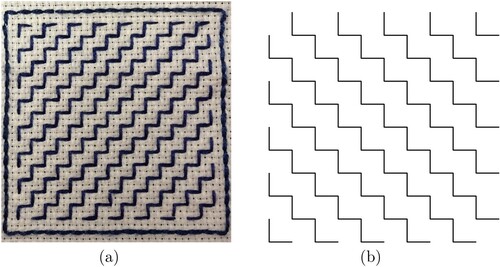
Figure 8. (a) Offset ten-crosses (jūjizashi). In the orientation shown the encoding is $v$ = 011; $w$ = 0110. (b) Encoded with different words, the crosses are aligned and mouth stitches form between them; this pattern is self-dual. It is discussed in Section 3.

Figure 9. (a) hirayama michi (drawn) with the features aligned, encoded $v$ = 1; $w$ = 10. (b) The surface of a pincushion has been stitched with a variant form, wherein the features face away from each other. The encoding is $v$ = 1; $w$ = 0110.

Figure 10. (a) The basic mountain form yamagata, encoded by changing the word from $v$ = 01 to $\tilde{v}$ = 10 at the chosen position of the peak, with $w$ = 01. (b) Double mountain form nijū yamagata which can be worked as a regular repeating design of any height. As shown, the encoding is $v$ = 10101; $w$ = 10.

Figure 11. (a), (b) Further variants of yamagata, both extending to the edge of the worked area. (c) The dual of both variants: of (a) if just the lower part is considered, and of (b) if just the upper part is considered.

Figure 12. (a) A persimmon (kaki) fruit with sepals, part of the flower (hana) remaining when the fruit forms, and (b) the stitch named kakinohanazashi. The pattern is generated by the words $v$ = 010 and $w=u\tilde{u}$ where $u$ = 1010.

Figure 13. The dual pattern to kakinohanazashi. This piece also demonstrates another way to make hitomezashi stitches of the same length, using a piece of polka-dot or checked fabric to provide a grid.

Figure 14. The three closed loops of stitching forming each flower give this stitch pattern the name triple persimmon flower stitch (sanjū kakinohanazashi). The encoding is $v$ = 01010; $w=u\tilde{u}$ where $u$ = 101010.

Figure 15. (a) Igetazashi or well-kerb stitch. The encoding is $v=w=u\tilde{u}$ where $u$ = 100. (b) The dual fabric.

Table 1. Features of the largest loops appearing in some traditional hitomezashi patterns.

Pattern name	Perimeter	Area	Height	Width
kuchizashi	4	1	1	1
jūjizashi	12	5	3	3
kakinohanazashi	20	13	5	5
dual sanjū kakinohanazashi	28	25	7	7
sanjū kakinohanazashi	36	41	9	9
igetazashi	28	17	5	5

Figure 16. Within this fully packed loop diagram for the permutation indicated by the numbers along the bottom, Fibonacci snowflakes of orders one, two, and four occur. A zig-zag pattern of line segments is disrupted at each of the vertices marked with a solid dot. Identifying vertices of the $32\times 32$ grid with entries in the permutation matrix, these dots correspond to entries which are 1 rather than 0. Note that there is only one such entry (or dot) in each row or column. Reproduced from Labbé (2010) with permission.

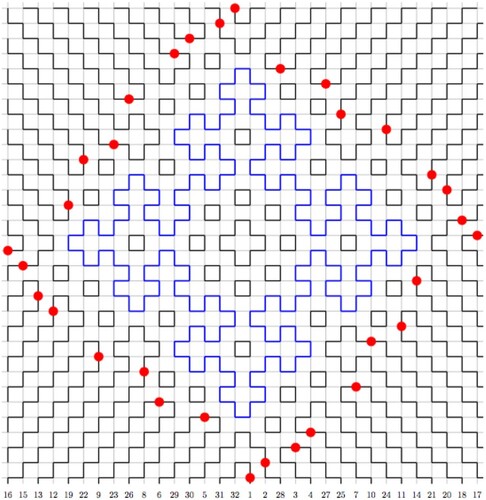
Figure 17. The Fibonacci snowflakes of order one, two, and three. The outline of each is traced by concatenating a word generated from Equation (1(1) $q_n=\{\begin{array}{ll}{q}_{n-1}{q}_{n-2}& n\equiv 2\mathrm{mod}3\\ q_{n-1}\overline{q_{n-2}}& n\equiv 0,1\mathrm{mod}3\end{array}$(1) ) four times. On each snowflake, the sequence of right and left steps for one word is shown. The dashed line indicates how the order one object forms inside the order three object if it is, rather, stitched using vertical and horizontal lines of running stitch.

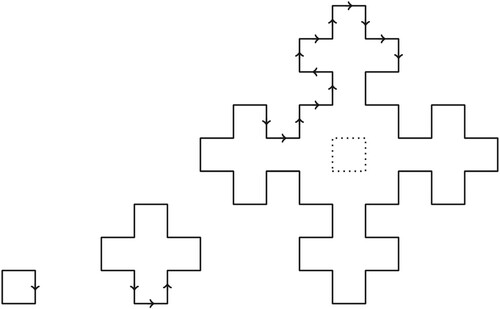
Figure 18. Tiling of the plane by order 3 Fibonacci snowflakes. Note however that this design cannot be stitched as hitomezashi, because there are vertices of order 4. This figure is inspired by Figure 2 of the paper by Blondin-Massé et al. (2013).

Figure 19. Two flags featuring Fibonacci snowflakes, from a strip of bunting. The flag on the right is the dual of the one on the left, apart from the border.

Figure 20. A single Fibonacci snowflake of order 5 extends from the top to bottom and left to right of this photo. Like Figure 1, it is a detail from a piece (60 by 84 cm) Cross and Crown stitched in 2022.

Figure 21. The whole bunting. The left-most flag and the two in the centre feature Pell persimmon polyomino patterns as defined in this paper. The remaining three feature generalizations to be explored further in future.

Labbé, S. (2010, October 22). Fibonacci tiles can appear in a fully packed loop diagram. Sébastien Labbé Blogue. http://www.slabbe.org/blogue/2010/10/fibonacci-tiles-can-appear-in-a-fully-packed-loop-diagram/.

 Google Scholar

Blondin-Massé, A., Brlek, S., Labbé, S., & Mendès France, M. (2013). Fibonacci snowflakes. Annales Mathematiques du Quebec, 35(2), 141–152.

 Google Scholar