Figures & data
Figure 1. The unit square S for the survivorship parameters s
1 and s
2 in the competition model Equation(8) is partitioned into to sub-regions S
1 and S
2 corresponding to the two case in Theorems 3.3.
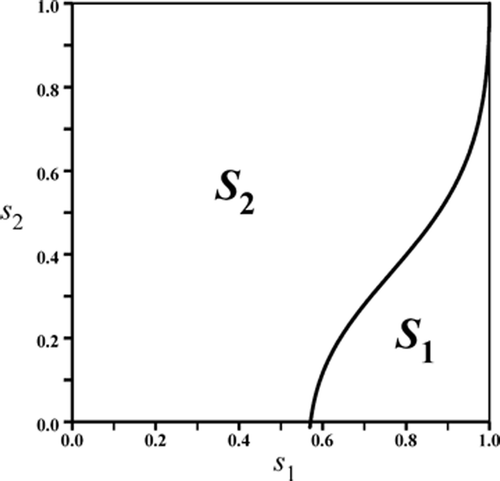
Figure 2. Each plot shows a solution of the Ricker competition model Equation(8) with b
1=8, b
2=10, s
1=0.65, s
2=0, r=1.1 and c=1.9. In plot (a) the initial conditions (x
0, y
0)=(0.2, 3.5) lead to competitive exclusion. In (b) the initial conditions (x
0, y
0)=(0.19, 3.5) lead to a competitive coexistence 2-cycle. See .
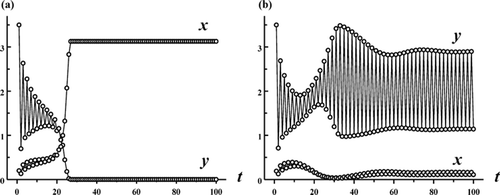
Figure 3. A sequence of phase plane plots shows the bifurcation of stable coexistence 2-cycles from the exclusion 2-cycles on the y-axis in the Ricker competition model Equation(8) as the competition coefficient c decreases through the critical value c*≈2.35. Model parameters are b
1=8, b
2=10, s
1=0.65, s
2=0, and r=1.1. Plot (a) shows a sequence of stable 2-cycles (open circles with connecting lines) that eventually destabilize and give rise to stable, double invariant loops as shown in plot (b). In plot (c) the double invariant loops eventually collide, under further decreases in c, and undergo a global, heteroclinic bifurcation involving the (saddle) coexistence equilibrium, the exclusion (saddle) equilibrium, the exclusion (saddle) 2-cycle located and their stable and unstable manifolds. For the parameter values in these plots, the exclusion equilibrium E
1:(x, y)≈(22.86, 0) is also stable and hence these plots contain multiple mixed-type attractors.
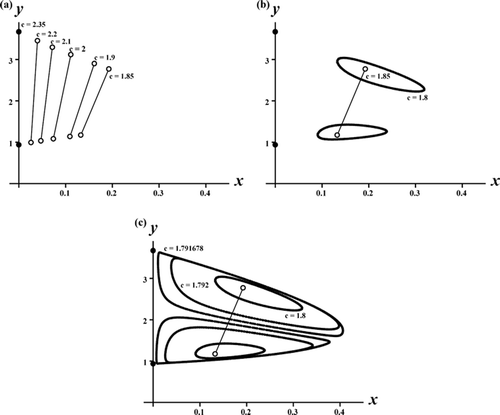
Figure 4. Each graph shows a solution of the Ricker competition model Equation(8) with b
1=8, b
2=10, s
1=0.65, s
2=0, r=1.1 and c=1.8. In plot (a) the initial conditions (x
0, y
0)=(0.12, 3.5) lead to competitive exclusion. In plot (b) the initial conditions (x
0, y
0)=(0.01, 3.5) lead to a competitive coexistence quasi-periodic oscillation (see , c)).
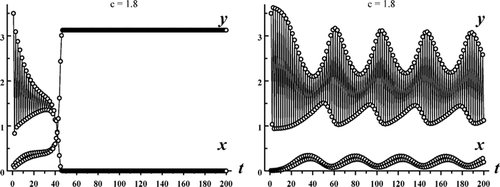
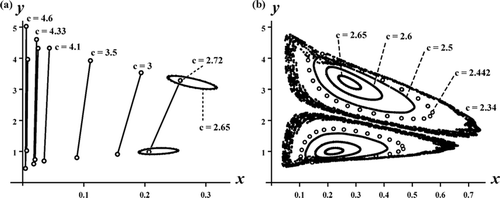
Figure 5. A sequence of phase plane plots shows the bifurcation of stable coexistence 4-cycles from the exclusion 4-cycles on the y-axis in the Ricker competition model Equation(8) as c decreases from the critical value c*≈4.77. Model parameters are b
1=8, b
2=14, s
1=0.8, s
2=0, r=0.8 and c=1.9. Plot (a) shows a sequence of 4-cycles the undergoes a period-halving bifurcation to 2-cycles which ultimately destabilize and give rise to stable, double invariant loops. As c decreases further, plot (b) shows the double invariant loops, which occasionally period lock, eventually giving rise to chaotic attractors. The chaotic attractors suddenly disappears when an ‘interior crisis’ occurs at a critical value of c. For the parameter values in these plots, the exclusion equilibrium E
1:(x, y)≈(3.69, 0) is also stable and hence these plots contain multiple mixed-type attractors.