Figures & data
Figure 1. Critical Allee type per capita growth rates h(x) for p=6 (left) and p=1.5 (right).
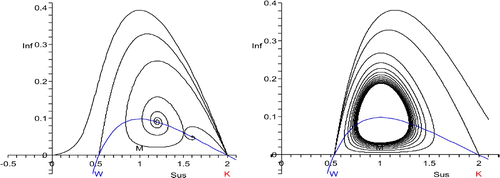
Figure 2. W<S*<K. Left: S* close to W, host disappearance. The unstable manifold of (K, 0) connects to (0,0), the stable manifold of (W, 0) connects to (S*, I*), which is an unstable spiral point. Right: S* close to K, host decline to the endemic equilibrium (S*, I*), which is a stable focus. The stable manifold of (W, 0) separates the basins of attraction of (0, 0) and (S*, I*). The unstable manifold of (K, 0) connects to (S*, I*). In the left figure, the unstable manifold of (K, 0) lies above the stable manifold of (W,0), whereas it is the other way around in the right figure. As S* is moved from W to K, one expects that the two manifolds meet for a particular value of S*.
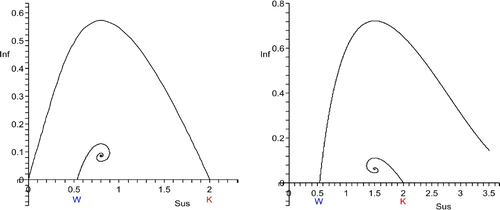
Figure 3. W<S*<K, transition from host decline to host disappearance for p=6. The unstable manifold of (K, 0) is shown for four values of S*. The values of S* can be identified from where the orbits end or where they take their maximum. The Hopf bifurcation at S*=1 is supercritical. So there is coexistence both at equilibrium and in periodicity. The second orbit from above is heteroclinic.
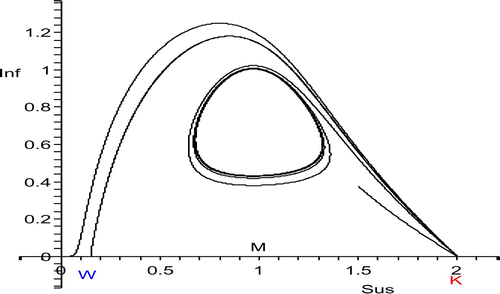
Figure 4. W<S*<K, transition from host decline to host disappearance for p=1.5: on the left, the unstable manifolds of (K, 0) and on the right the stable manifolds of (W, 0), for four values of S*, respectively. The orbits take their maximum at S*. The choices of S* are not the same on the left and the right. The Hopf bifurcation at S*=1 is subcritical: there is no periodic coexistence. The second orbits from above are heteroclinic. One curve is the isocline for the infectives.
