Figures & data
Figure 1. Three phase planes for the MacArthur–Rosenzweig system (solid) and the corresponding system with quiescence (dashed, trajectories have been projected from four dimensions onto the u, v-plane). In each case, the MR system has a limit cycle. Left (just inside the stability region): the system with quiescence has a stable stationary point. Centre (deep inside the stability region): rapid convergence to stationary point. Right (outside the stability region): both systems have limit cycles. The projected limit cycle of the quiescent system is much smaller than that of the MR system.
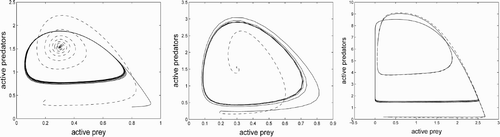
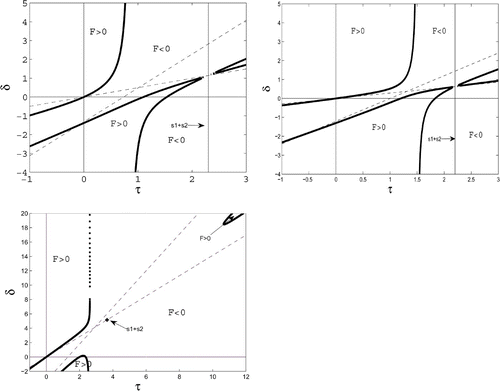
Figure 2. The τ, δ-plane with the null set of the cubic F and the second and third of the linear Hurwitz conditions (dashed). Quiescence leads to an enlarged stability domain that comprises the second quadrant and also the part of the first quadrant between the δ-axis and the upper branch of the null set. Broadly speaking, this domain gets larger when p 1, p 2 are increased. Case 1a. p 1=0.5, p 2=0.35, q 1=0.6, q 2=0.85, p<z 1<z 2. The first branch runs monotonely from (0, 0) to the vertical asymptote. Case 1b. p 1=1, p 2=0.5, q 1=0.2, q 2=0.5, z 1<p<z 2. The first branch runs monotonely from (0, 0) to the vertical asymptote. Case 2. p 1=1.1, p 2=1.5, q 1=0.9, q 2=0.15, z 1<z 2<p. The first branch runs from (0, 0) upward, crosses the vertical asymptote, turns back, and approaches the asymptote.