Figures & data
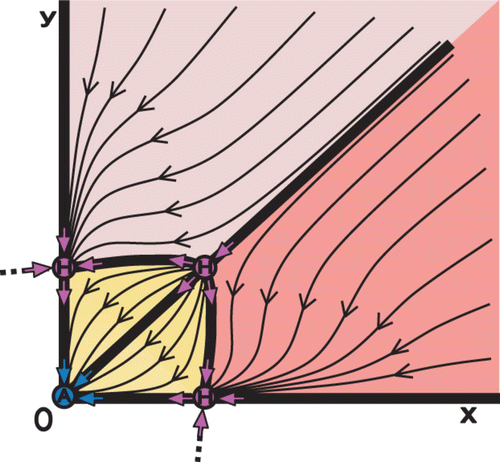
Figure 1. Phase space showing semistability (from the left) in accordance with the Examples 1–4. (a) Example 1: λ1=1 (W c), λ2=1/2<1 (W s). The left-hand side of the phase space imitates an Attractor (A) and the right-hand side a saddle point (S). The semistable point is indicated by H A . (b) Example 2: λ1=1 (W c), λ2=2>1 (W u). The left-hand side of the phase space imitates a saddle point (S) and the right-hand side a Repeller (R). The semistable point is indicated by H R . (c) Example 3 (without semistability): λ1=1 (W u), λ2=1/2<1 (W s). The fixed point is a saddle point (S). (d) Example 4 (without semistability): λ1=1 (W u), λ2=2>1 (W u). The fixed point is a Repeller (R).
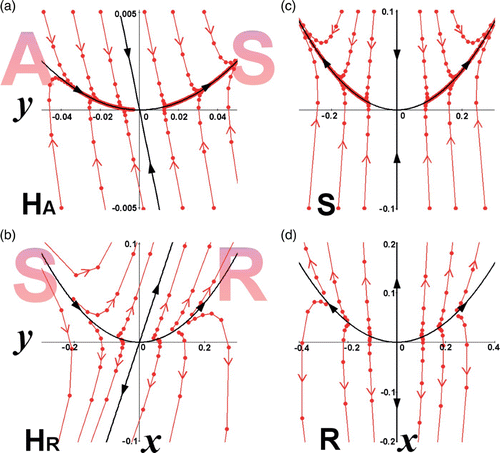
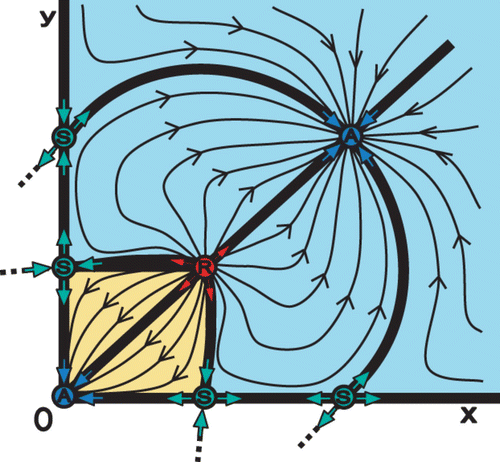
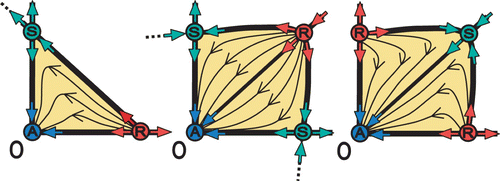
Figure 2. Two different types of semistable points H R and H A can be seen as ‘merging’ two ordinary fixed points through a bifurcation, that is a repeller (R) + a saddle (S) (upper graphs) (see also ), and an attractor (A) +a saddle (S) (lower graphs) (see also ).
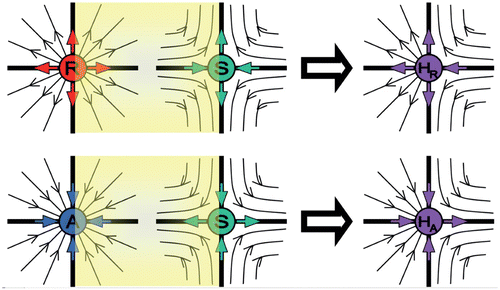
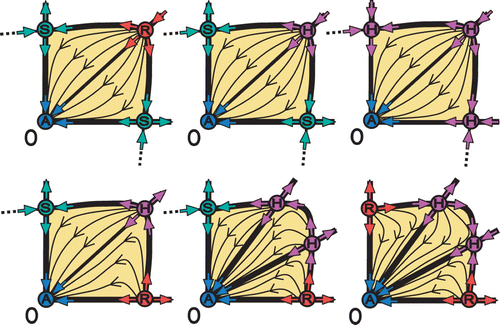
Figure 3. Semistable point H RA is created through a bifurcation of the ordinary fixed points of stability R and A, or of the first-generation semistability points H R and H A . The semistable point H RA on the top-right figure is a special case of the semistable point H RA depicted on the lower right figure, where the second and fourth quadrants that behave as a saddle S degenerate to a separatrix (coinciding with the vertical axis) that consists entirely of fixed points.
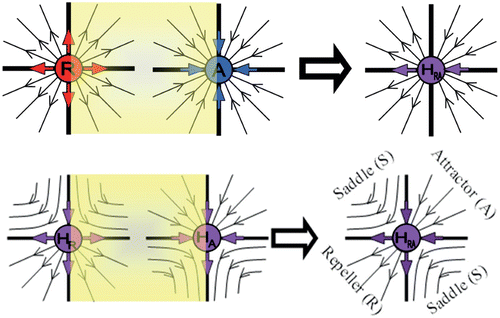
Figure 4. The phase space for the planar Λ-Ricker map Equation(5) with parameters Λ1=Λ2=2, b
1=b
2=c
1=c
2=1, k
1=k
2=1.7 (symmetric map).
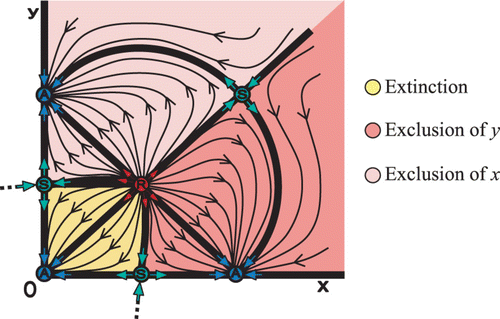
Figure 5. The phase space for the planar map of Equation(8) (competition model that exhibits contest inter-specific competition) and a selection of the parameter values a
1=a
2=2.5, b
1=b
2=0.1 (symmetric map).
Figure 6. A hypothetical phase space with only extinction and coexistence regions.
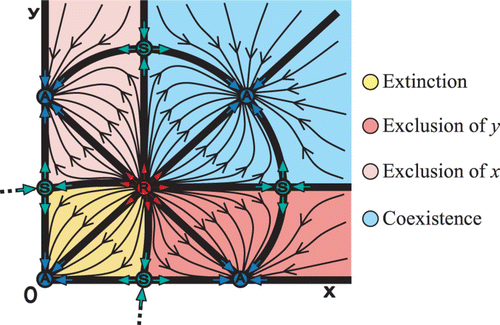
Figure 7. In the symmetric planar Λ-Ricker map, the two interior fixed points of a repeller (R) and a saddle (S) are merged through a bifurcation into one semistable fixed point when k=ln Equation(2). Panels show a gradual decrease of k: (a) k=1.7, (b) k=1 and (c) k=ln Equation(2)
. The generated semistable point (indicated by H) is of type H
R
().
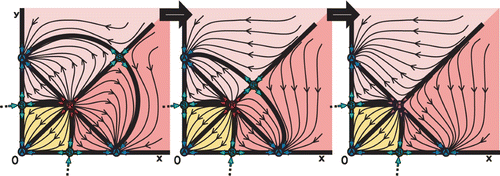
Figure 8. Phase space with three semistable points (indicated by H), two H A fixed points at each axis and one H R fixed point in the interior.
Figure 9. The three possible arrangements of fixed points that construct a core of the Allee effect.
Figure 10. Semistable fixed points H R and H A replace regular fixed points R and S, respectively, as it is shown in upper middle and right panels. The double role of H R (as R and S) and H A (as A and S) is shown in the lower panels. (Both H R and H A are indicated by H.)
