Survival analysis of a stochastic predator–prey model with prey refuge and fear effect

Figures & data

Figure 1. (a) and (c): The asymptotic behaviour of the solutions to stochastic model (2) around the positive equilibrium of model (1) with initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$; (b) and (d): The density function diagrams of $x\left(t\right)$ and $y\left(t\right)$, respectively. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and m = 0.1, K = 0.3, ${\sigma }_1={\sigma }_2=0.01$.

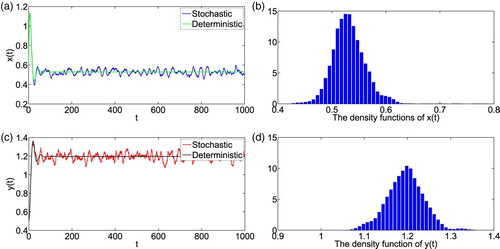
Figure 2. Numerical simulation for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x},\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x},\end{array}$(1) ) and model (2(2) $\begin{array}{rl}\mathrm{d}x& =\left[\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{1}x\mathrm{d}{B}_1\left(t\right),\\ \mathrm{d}y& =\left[-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{2}y\mathrm{d}{B}_2\left(t\right),\end{array}$(2) ) with initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and m = 0.1, K = 0.3, ${\sigma }_1=1.1$, ${\sigma }_2=0.01$.

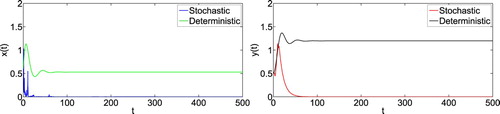
Figure 3. Numerical simulation for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x},\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x},\end{array}$(1) ) and model (2(2) $\begin{array}{rl}\mathrm{d}x& =\left[\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{1}x\mathrm{d}{B}_1\left(t\right),\\ \mathrm{d}y& =\left[-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{2}y\mathrm{d}{B}_2\left(t\right),\end{array}$(2) ) with initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and m = 0.1, K = 0.3, ${\sigma }_1=0.1$, ${\sigma }_2=0.9$.

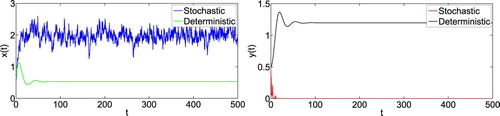
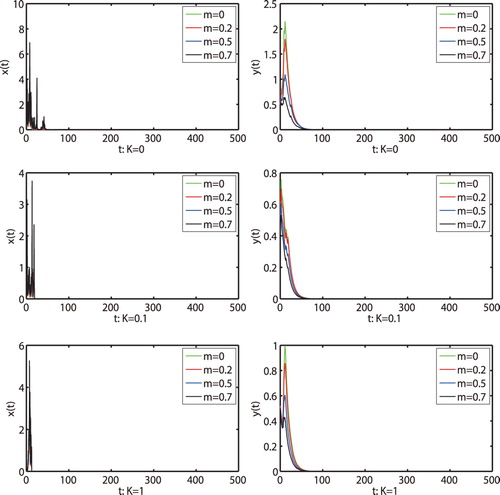
Figure 4. Numerical simulation for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x}{\mathrm{d}t}& =\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x},\\ \frac{\mathrm{d}y}{\mathrm{d}t}& =-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x},\end{array}$(1) ) and model (2(2) $\begin{array}{rl}\mathrm{d}x& =\left[\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{1}x\mathrm{d}{B}_1\left(t\right),\\ \mathrm{d}y& =\left[-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{2}y\mathrm{d}{B}_2\left(t\right),\end{array}$(2) ) with initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$ and different K, respectively. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and m = 0.1, ${\sigma }_1={\sigma }_2=0.01$.

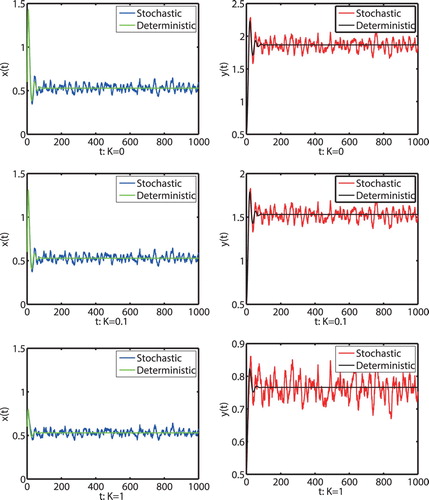
Figure 5. The solutions of model (2(2) $\begin{array}{rl}\mathrm{d}x& =\left[\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{1}x\mathrm{d}{B}_1\left(t\right),\\ \mathrm{d}y& =\left[-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{2}y\mathrm{d}{B}_2\left(t\right),\end{array}$(2) ) with the initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$ and different K,m, respectively. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and ${\sigma }_1={\sigma }_2=0.01$.

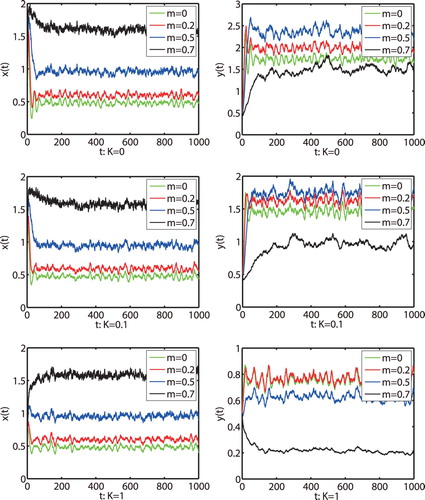
Figure 6. The solutions of model (2(2) $\begin{array}{rl}\mathrm{d}x& =\left[\frac{\alpha x}{1+Ky}-b{x}^2-\frac{\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{1}x\mathrm{d}{B}_1\left(t\right),\\ \mathrm{d}y& =\left[-\gamma y+\frac{c\text{β}(1-m)xy}{1+a(1-m)x}\right]\mathrm{d}t+{\sigma }_{2}y\mathrm{d}{B}_2\left(t\right),\end{array}$(2) ) with the initial value $\left(x\right(0),y(0\left)\right)=(0.6,0.5)$ and different K,m, respectively. The parameters are taken as (23(23) $\alpha =0.6,b=0.3,\text{β}=0.3,c=0.8,a=0.3,\gamma =0.1,$(23) ) and ${\sigma }_1=1.1,{\sigma }_2=0.01$.