Figures & data
Figure 1. The division of the -plane depending on the signs of
,
and
. It shows that the curves
,
and
divide the
-plane into six subregions:
,
,
,
,
and
. There exist two positive equilibria in subregion
(yellow), a unique positive equilibrium in subregions
and two curves
for
, and
for
(red), and no positive equilibria in subregions
together with the curve
for
(blue).
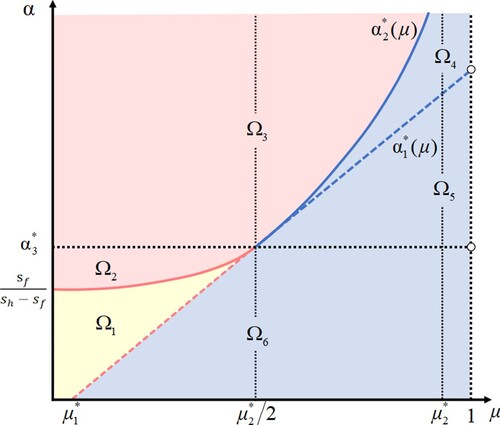
Figure 2. Given and
, we have
. For the case
, we get
,
. Numerical trials imply that
. Taking
, we have
,
and
. At
,
and
. Furthermore, when increasing β to 0.004, both
and
vanish, and
.
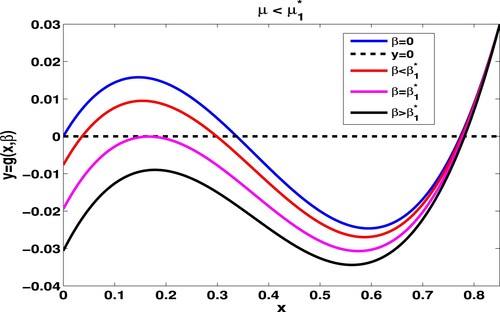
Figure 3. Given and
, we take
. When
,
and
coincide to
. Numerical trials offer
. When
,
,
and
. When
, both
and
coincide to
and
. For
,
.
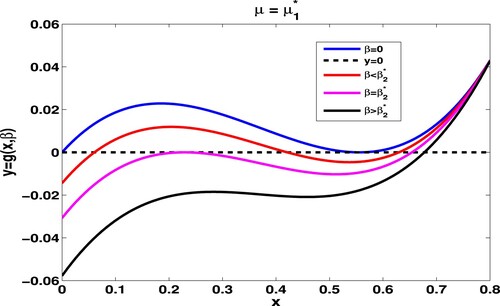
Figure 4. Given and
, we take
. Numerical simulations show that
,
. The number of zeros of
lying in
goes from 1, passing 2, 3, 2, and finally to 1 as β increases from 0 to the β with
.
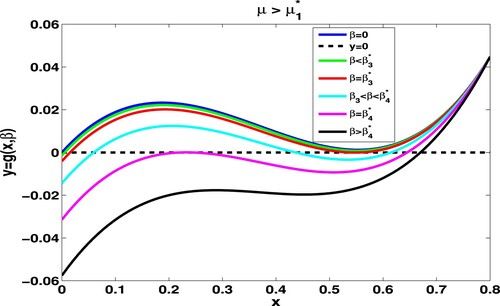
Figure 5. Distable dynamics driven by model (Equation4(4)
(4) ) and model (Equation16
(16)
(16) ). Panel (A) is for model (Equation4
(4)
(4) ) and Panel (B) is for model (Equation16
(16)
(16) ).
![Figure 5. Distable dynamics driven by model (Equation4(4) xn+1=(1−μ)(1−sf)(1+α)xnshxn2−[sf+sh+α(sf−sh)]xn+1+α(1−sh),n=0,1,2,….(4) ) and model (Equation16(16) xn+1=(1−μ)(1−sf)(β+xn)shxn2−(sf+sh)xn+1+β(1−sf),n=0,1,2,….(16) ). Panel (A) is for model (Equation4(4) xn+1=(1−μ)(1−sf)(1+α)xnshxn2−[sf+sh+α(sf−sh)]xn+1+α(1−sh),n=0,1,2,….(4) ) and Panel (B) is for model (Equation16(16) xn+1=(1−μ)(1−sf)(β+xn)shxn2−(sf+sh)xn+1+β(1−sf),n=0,1,2,….(16) ).](/cms/asset/4095c98a-5a3d-450d-826d-5d0e5a59fb94/tjbd_a_1977400_f0005_oc.jpg)
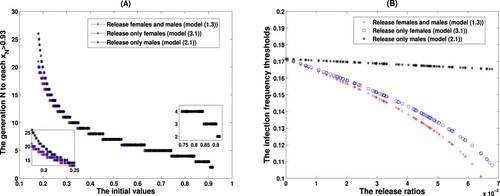
Figure 6. Comparisons on the infection frequency thresholds (A) and the polymorphic states (B) driven by (Equation3(3)
(3) ), (Equation16
(16)
(16) ) and (Equation4
(4)
(4) ) on different maternal leakage rates μ lying in
.
![Figure 6. Comparisons on the infection frequency thresholds (A) and the polymorphic states (B) driven by (Equation3(3) xn+1=(1−μ)(1−sf)(1+r)(xn+r)shxn2−sf+sh+r(sf−sh)xn+1+(2−sf−sh)r+(1−sf)r2,n=0,1,2,…(3) ), (Equation16(16) xn+1=(1−μ)(1−sf)(β+xn)shxn2−(sf+sh)xn+1+β(1−sf),n=0,1,2,….(16) ) and (Equation4(4) xn+1=(1−μ)(1−sf)(1+α)xnshxn2−[sf+sh+α(sf−sh)]xn+1+α(1−sh),n=0,1,2,….(4) ) on different maternal leakage rates μ lying in (0,μ1∗).](/cms/asset/1a54df55-63d4-4227-89d5-4fcc3e61ca7f/tjbd_a_1977400_f0006_oc.jpg)