Technique to derive discrete population models with delayed growth

Figures & data

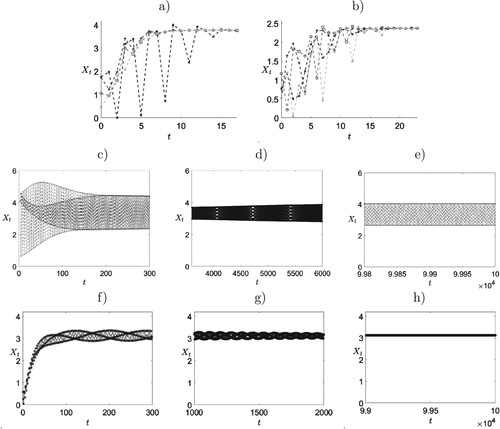
Figure 1. Orbit diagram for (14(14) $X_{t+1}=\frac{X_t}{1+\sum _{i=0}^3{a}_i{X}_t^i}+\frac{r{X}_{t-\tau }}{1+\sum _{i=0}^3{c}_i\left(\tau \right)X_{t-\tau }^i}$(14) ) created with Matlab [23]. (a) We plotted the last 1000 values of a total of 51000 iterations for randomly chosen positive initial conditions. $X_{\mathrm{\infty }}$ denotes the limiting behaviour of the simulated orbit. For small delay, there does not appear to be a stable equilibrium. Increasing the delay sufficiently, stabilizes a positive equilibrium. However, as predicted by Theorem 3.5, increasing the delay beyond ${\tau }_c$ results in extinction. (b) We plotted the last 100 values of a total of ${10}^7$ iterations for $\tau \in \{35,36,\dots ,55\}$ to demonstrate the type of dynamics that can occur when the positive equilibrium loses stability.

Figure 2. Solutions of (23(23) $X_{t+1}=H(X_t,X_{t-\tau }):=\frac{1}{1+d+c{X}_t}{X}_t+\frac{D}{D\text{β}+(\text{β}-1)Cr{X}_{t-\tau }}r{X}_{t-\tau }t\ge \tau ,$(23) ) with parameter values $d=0.2$, $c=1$, $C=0.5$, $D=0.5$, and $r=2.5$ for different positive initial conditions. In (a), $\tau =3<{\tau }_c=5.68$. As predicted by Theorem 4.5, for $\tau <{\tau }_c$, all solutions converge to the unique positive equilibrium. In (b), $\tau =6>{\tau }_c$. Solutions converge to the only non-negative equilibrium $X_0^{\ast }=0$, as predicted by Theorem 4.3, although the convergence appears to be slow.

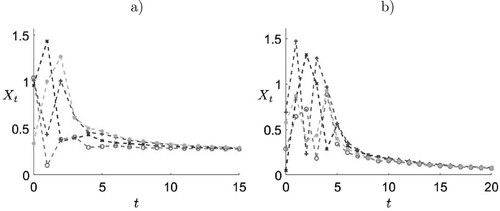
Figure 3. Solutions of (33(33) $X_{t+1}=H_R(X_t,X_{t-\tau }):=e^{-d-c{X}_t}{X}_t+\frac{D}{D\text{β}+(\text{β}-1)RC{X}_{t-\tau }}R{X}_{t-\tau },$(33) ). In all cases the initial conditions were generated randomly. (a)–(b) The parameter values are $d=0.1,c=1,C=0.05,D=0.1,R=10.$ For the given parameter values $\lceil {\tau }_c\rceil =47.$ In (a), $\tau =3$, resulting in $X_1^{\ast }\approx 3.770<z_r\approx 4.967$. In (b), $\tau =5$, resulting in $X_1^{\ast }=2.372<z_r\approx 3.584$. In both cases, solutions converge to $X_1^{\ast }$, as predicted by Theorem 4.15(i). In (c)–(e) parameter values are $d=0.01,D=1,c=1,C=0.001,R=16.2$ and $\tau =3$. Here, ${\tau }_c=9.6690$ and $X_1^{\ast }=3.3138>z_r\approx 3.287$. Theorem 4.15(ii) predicts that $X_1^{\ast }$ is unstable. The solution converges to a period two cycle. (f)–(h) The parameter values are $c=1,d=0.1,D=1,C=0.001,R=7.7$, $\tau =2$. Here, $X_1^{\ast }\approx 2.795>2c^{-1}=2$, $z_r\approx 2.275$, and ${\omega }_r\approx 15.152$. Thus, $X_1^{\ast }\in (max\{2c^{-1},z_r\},{\omega }_r)$ and Theorem 4.15 is inconclusive. However, the simulation shows convergence to $X_1^{\ast }$.

MATLAB, Version R2021a. The MathWorks Inc., Natick, Massachusetts, 2021.

 Google Scholar