The performance of zero-cost option derivative strategies during turbulent market conditions in developing and developed countries

Figures & data

Table 1. Volatility modelled index summary

Index	Name	Volatility Index used	Developed/Developing economy
S&P 500	Standard & Poor’s 500	Chicago Board Options Exchange Volatility Index	Developed
NIKKEI 225	Nikkei Stock Average	Volatility Index Japan	Developed
FTSE 100	Financial Times Actuaries 100 Index	Implied Volatility Index Series	Developed
JSE ALSI	Johannesburg Stock Exchange All Share Index	South African Volatility Index	Developing
BOVESPA	IBOVESPA	Chicago Board Options Exchange Brazil ETF Volatility Index	Developing
RTSI	Russian Trading System Index	Russian Volatility Index	Developing

Source: Author compilation

Table 2. Risk-free rate index summary

Index	Name	Risk-free rate used
S&P 500	Standard & Poor’s 500	Federal Funds Rate
NIKKEI 225	Nikkei Stock Average	Japan Government Bond 10-year bond rate
FTSE 100	Financial Times Actuaries 100 Index	London Interbank Offer Rate
JSE ALSI	Johannesburg Stock Exchange All Share Index	Johannesburg Interbank Agreed Rate
BOVESPA	IBOVESPA	Brazil Government Bond 10-year bond rate
RTSI	Russian Trading System Index	Russia Government Bond 10-year bond rate

Table 3. Summary of strategy returns

	ZCC
Floor return	$-\theta$
Cap return	$K_c-S_0{S}_0$
Strategy return	In the range $K_p\le I\le K_c$ the return is $I-S_0{S}_0$

Figure 1. Relative performance of the six indices from January 1995 to December 2020.

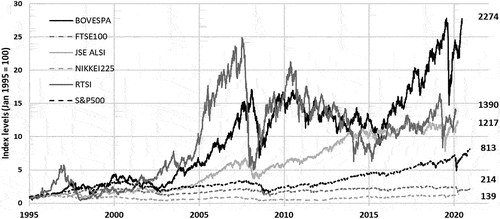
Figure 2. (a,b,c): Relative performance of the six developing economies indices from January 1995 to December 2020. (d,e,f): Relative performance of the six developed economies indices from January 1995 to December 2020.

Figure 2. Continued.

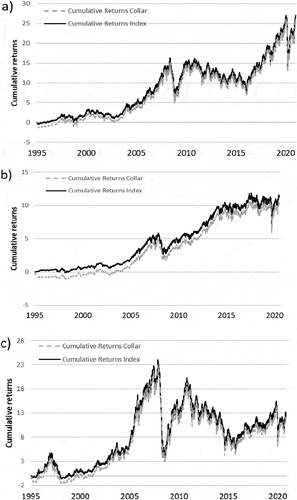
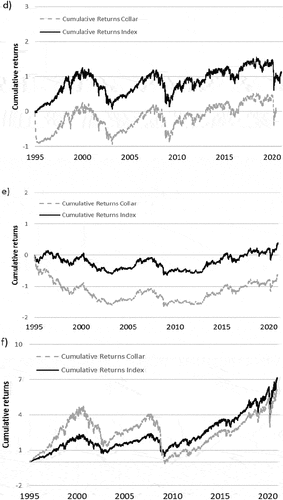
Figure 3. (a): Cumulative returns of the S&P 500 Index and increasing put option strike prices. (b): Cumulative returns of the NIKKEI 225 Index and increasing put option strike prices. (c): Cumulative returns of the FTSE 100 Index and increasing put option strike prices. (d): Cumulative returns of the JSE ALSI Index and increasing put option strike prices. (e): Cumulative returns of the BOVESPA Index and increasing put option strike prices. (f): Cumulative returns of the RTSI Index and increasing put option strike prices.

Source: Author compilation

Figure 3. Continued.

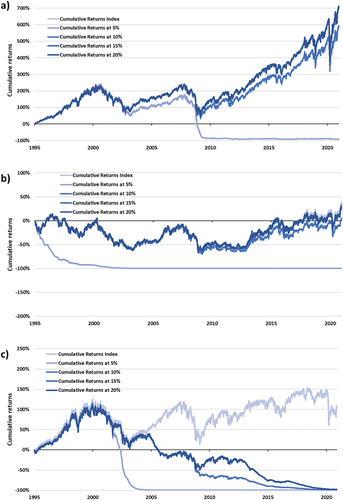
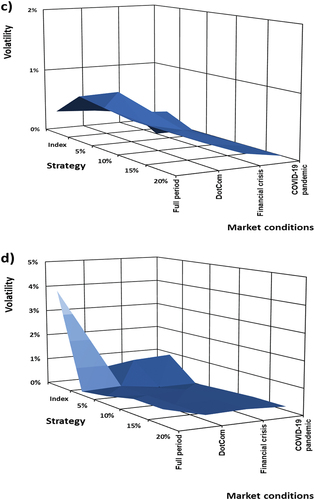
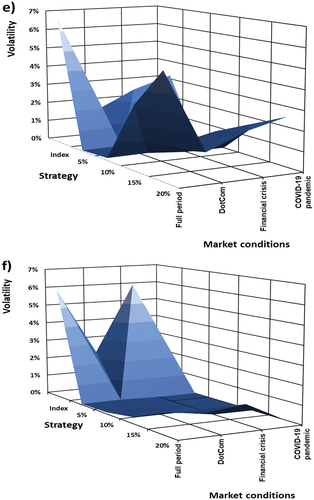
Figure 4. (a): Volatility levels for the ZCC implemented on the S&P 500 indices as underlying, as a function of put option strike levels and turbulent market conditions. (b): Volatility levels for the ZCC implemented on the NIKKEI 225 as underlying, as a function of put option strike levels and turbulent market conditions. (c): Volatility levels for the ZCC implemented on the FTSE 100 indices as underlying, as a function of put option strike levels and turbulent market conditions. (d): Volatility levels for the ZCC implemented on the JSE ALSI indices as underlying, as a function of put option strike levels and turbulent market conditions. (e): Volatility levels for the ZCC implemented on the BOVESPA as underlying, as a function of put option strike levels and turbulent market conditions. (f): Volatility levels for the ZCC implemented on the RTSI indices as underlying, as a function of put option strike levels and turbulent market conditions.

Figure 4. Continued.

Figure 4. Continued.

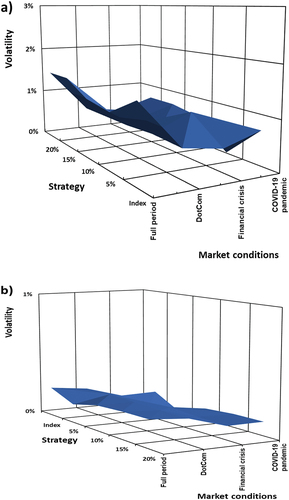
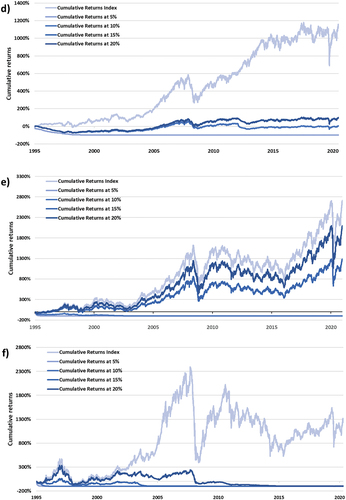
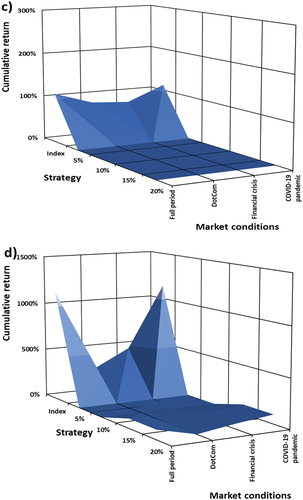
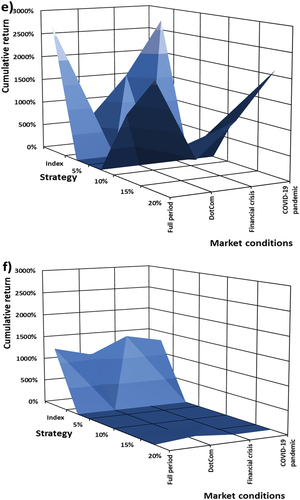
Figure 5. (a): Cumulative return as a function of put option strike levels and turbulent market conditions on the S&P 500. (b): Cumulative return as a function of put option strike levels and turbulent market conditions on the NIKKEI 225. (c): Cumulative return as a function of put option strike levels and turbulent market conditions on the FTSE 100. (d): Cumulative, as a function of put option strike levels and turbulent market conditions on the JSE ALSI. (e): Cumulative, as a function of put option strike levels and turbulent market conditions on the BOVESPA. (f): Cumulative, as a function of put option strike levels and turbulent market conditions on the RTSI.

Figure 5. Continued.

Figure 5. Continued.

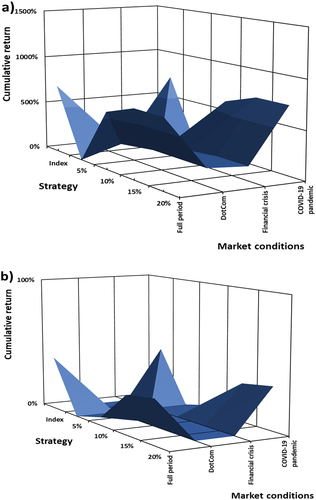
Table 4. Summary of ZCC strategy statistics and performance in the Dotcom bubble

UI	Market conditions (1995–2005)			ZCC
	$\sigma$	$r_c$	Environment
S&P 500	$5,8\%$	$177\%$	• Moderate $\sigma$, moderate growth • Losses due to DC but small compared with other developed economies	• $-0,27\%r_c+235\%$ • Increases for $K_p+5\%$
NIKKEI 225	$2\%$	$-17\%$	• Low $\sigma$, negative growth • Largest losses due to DC • Overall loss due to low $\sigma$	• $-62\%r_c+15\%$ • Worst performer $\forall K_p$ • Flat for $K_{p}5\%$
FTSE 100	$3,2\%$	$85\%$	• Low $\sigma$, moderate growth • Moderate losses due to DC	• $-4\%r_c+125\%$ • Flat for $K_{p}5\%$
BOVESPA	$16\%$	$683\%$	• High $\sigma$, high growth • Losses due to DC but small compared with other developing economies	• $-50\%r_c+686\%$ • Second best performer $\forall K_p$ • Flat for $K_{p}5\%$
JSE ALSI	$5,8\%$	$280\%$	• Moderate $\sigma$, moderate growth	• $-12\%r_c+280\%$ • Third best performer $\forall K_p$ • Increases for $K_{p}10\%$
RTSI	$23,4\%$	$1095\%$	• High $\sigma$, high growth • Losses due to DC but small compared with other developing economies	• $-62\%r_c+1094\%$ • Best performer $\forall K_p$ • Flat for $K_{p}5\%$

UI underlying index

DC dot-com bubble of 1995–2005

$r_c$ cumulative return

Table 5. Summary of ZCC strategy statistics and performance in the financial crisis

UI	Market conditions (2008/2009)			ZCC
	$\sigma$	$r_c$	Environment
S&P 500	$4,6\%$	$147\%$	• Moderate $\sigma$, moderate growth • Losses due to FC but small compared with other developed economies	• $47\%r_c+215percent$ • Increases for $K_p+10\%$
NIKKEI 225	$1,1\%$	$-47\%$	• Low $\sigma$, negative growth • Largest losses due to FC • Overall loss due to low $\sigma$	• $-64\%r_c-25\%$ • Worst performer $\forall K_p$ • Increases for $K_{p}10\%$
FTSE 100	$2,4\%$	$79\%$	• Low $\sigma$, moderate growth • Moderate losses due to FC	• $14\%r_c+110\%$ • Increases for $K_{p}5\%$
BOVESPA	$26\%$	$1540\%$	• High $\sigma$, high growth • Losses due to FC but small compared with other developing economies	• $588\%r_c+1621\%$ • Best performer $\forall K_p$ • Flat for $K_{p}5\%$
JSE ALSI	$8,2\%$	$477\%$	• Moderate $\sigma$, high growth • Losses due to FC but small compared with other developing economies	• $266\%r_c+589\%$ • Third best performer $\forall K_p$ • Flat for $K_p>5\%$
RTSI	$61\%$	$1455\%$	• High $\sigma$, high growth • Losses due to FC but small compared with other developing economies	• $389\%r_c+2397\%$ • Second best performer $\forall K_p$ • Flat for $K_{p}5\%$

UIunderlying index

FCfinancial crisis of 2008/9

$r_c$cumulative return.

Source: Author compilation

Table 6. Summary of ZCC strategy statistics and performance in the COVID-19 pandemic

UI	Market conditions (2008/2009)			ZCC
	$\sigma$	$r_c$	Environment
S&P 500	$7\%$	$714\%$	• Moderate $\sigma$, high growth • Losses due to C-19 but small compared with other developed economies	• $+388\%r_c+716\%$ • Increases for $K_p>+5\%$
NIKKEI 225	$1,2\%$	$40\%$	• Low $\sigma$, low growth • Largest losses due to C-19	• $-16\%r_c+40\%$ Worst performer $\forall K_p$ • Increases for $K_{p}5\%$
FTSE 100	$7\%$	$113\%$	• Low $\sigma$, moderate growth • Moderate losses due to C-19	• $+62\%r_c+149\%$ • Flat for $K_{p}5\%$
BOVESPA	$32\%$	$2711\%$	• High $\sigma$, high growth • Losses due to C-19 but small compared with other developing economies	• $+1395\%r_c+2711\%$ • Best performer $\forall K_p$ • Flat for $K_{p}5\%$
JSE ALSI	$9,2\%$	$1140\%$	• Moderate $\sigma$, high growth • Losses due to C-19 but small compared with other developing economies	• $+689\%r_c+1158\%$ • Third best performer $\forall K_p$ • Increases for $K_{p}10\%$
RTSI	$16,3\%$	$1296\%$	• High $\sigma$, high growth • Losses due to C-19 but small compared with other developing economies	• $+730\%r_c+1543\%$ • Second best performer $\forall K_p$ • Flat for $K_{p}5\%$

UI underlying index

C-19 COVID-19 pandemic of 2020.

$r_c$ cumulative return.