Advanced search
Publication Cover
Statistical Theory and Related Fields Volume 5, 2021 - Issue 1
Submit an article Journal homepage
558
Views
1
CrossRef citations to date
0
Altmetric
Articles

Efficient estimation of smoothing spline with exact shape constraints

Vincent Chana Department of Statistics, University of Wisconsin-Madison, Madison, WI, USAView further author information
,
Kam-Wah Tsuia Department of Statistics, University of Wisconsin-Madison, Madison, WI, USAView further author information
,
Yanran Weib Department of Statistics, Virginia Tech, Blacksburg, VA, USAORCID Iconhttps://orcid.org/0000-0002-6745-7326View further author information
ORCID Icon,
Zhiyang Zhangb Department of Statistics, Virginia Tech, Blacksburg, VA, USAView further author information
&
Xinwei Dengb Department of Statistics, Virginia Tech, Blacksburg, VA, USACorrespondence[email protected]
ORCID Iconhttps://orcid.org/0000-0002-1560-2405View further author information
ORCID Icon
Pages 55-69 | Received 14 Feb 2019, Accepted 24 Jan 2020, Published online: 07 Feb 2020

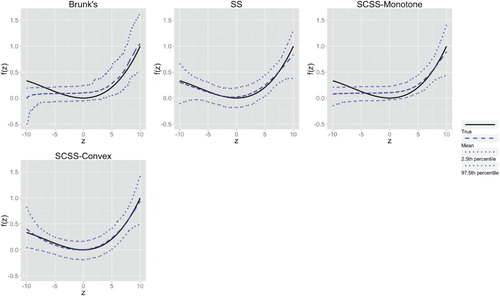
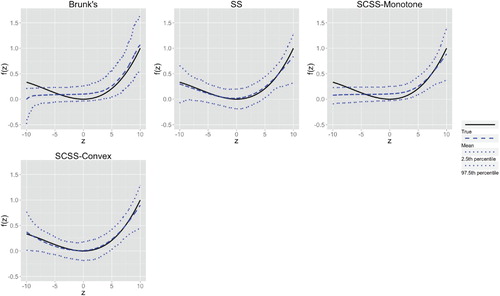
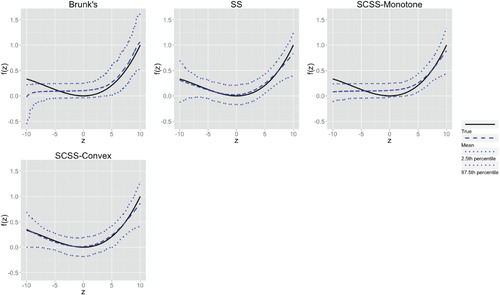
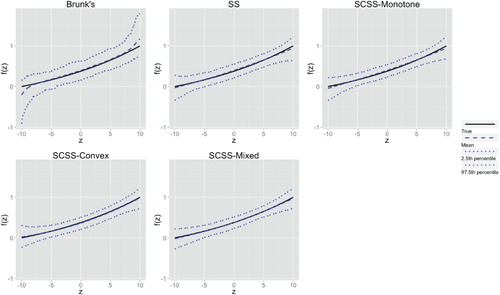
Figures & data

Figure 1. Comparison of the five true functions used in simulation studies.

Figure 1. Comparison of the five true functions used in simulation studies.

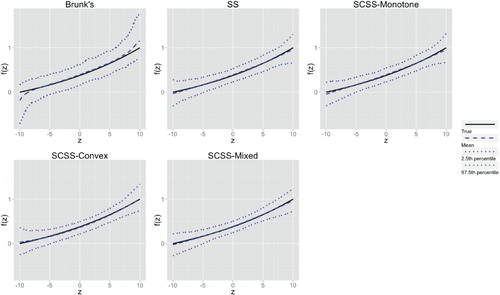
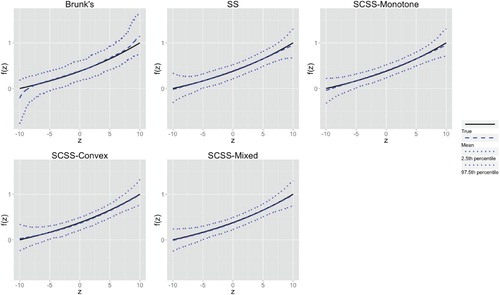
Table 1. Simulation studies comparing SCSS and other estimators under different functions and errors settings.Averaged MSPE (×100) and its standard error (×100) over 500 repetitions are reported. NA entries correspond to methods with no applicable settings.

Figure 2. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and convex constraint.

Figure 2. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and convex constraint.

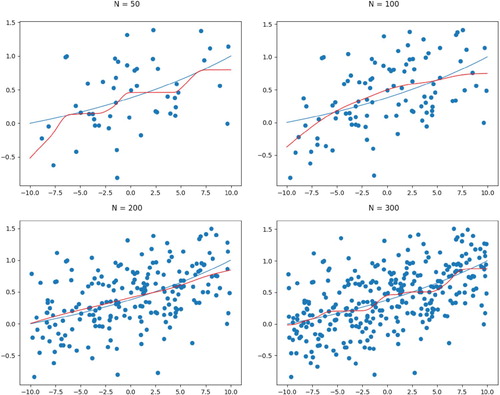
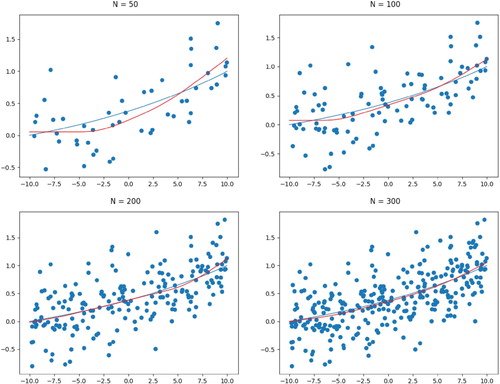
Table 2. Simulation studies measuring the convergence of SCSS based on the integrated mean squared errors.

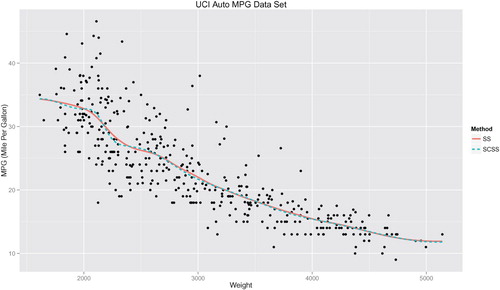
Figure 3. Comparison between unconstrained (SS) and monotone constrained (SCSS) smoothing spline for the Auto MPG Data. The response is mpg, modelled as a function of weight.

Figure 3. Comparison between unconstrained (SS) and monotone constrained (SCSS) smoothing spline for the Auto MPG Data. The response is mpg, modelled as a function of weight.

Figure 4. Comparison between unconstrained (SS) and monotone constrained (SCSS) smoothing spline for the Auto MPG Data. The response is mpg, modelled as a function of displacement.

Figure 4. Comparison between unconstrained (SS) and monotone constrained (SCSS) smoothing spline for the Auto MPG Data. The response is mpg, modelled as a function of displacement.

Figure A1. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under normal error.

Figure A1. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under normal error.

Figure A2. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under t error.

Figure A2. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under t error.

Figure A3. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under beta error.

Figure A3. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(20x2+x3)/3000 in Example 4 under beta error.

Figure A4. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error.

Figure A4. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error.

Figure A5. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under t error.

Figure A5. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under t error.

Figure A6. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under beta error.

Figure A6. The estimator percentiles (2.5% and 97.5%) of SCSS for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under beta error.

Figure A7. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and monotone constraint.

Figure A7. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and monotone constraint.

Figure A8. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and mixed constraint.

Figure A8. SCSS convergence for function f(x)=(ex/20−e−10/20)/(e10/20−e−10/20) in Example 5 under normal error and mixed constraint.

Reprints and Corporate Permissions

Please note: Selecting permissions does not provide access to the full text of the article, please see our help page How do I view content?

To request a reprint or corporate permissions for this article, please click on the relevant link below:

Order Reprints Request Corporate Permissions

Academic Permissions

Please note: Selecting permissions does not provide access to the full text of the article, please see our help page How do I view content?

Obtain permissions instantly via Rightslink by clicking on the button below:

Request Academic Permissions

If you are unable to obtain permissions via Rightslink, please complete and submit this Permissions form. For more information, please visit our Permissions help page.

Related research

People also read lists articles that other readers of this article have read.

Recommended articles lists articles that we recommend and is powered by our AI driven recommendation engine.

Cited by lists all citing articles based on Crossref citations.
Articles with the Crossref icon will open in a new tab.